A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику

Подождите немного. Документ загружается.

356 23 Conﬁdence intervals for the mean

23.4 We need to solve P(Z ≥ a)=0.01. In Table B.1 we ﬁnd P(Z ≥ 2.33) =

0.0099 ≈ 0.01, so z

0.01

≈ 2.33. For z

0.95

we need to solve P(Z ≥ a)=0.95,

and because this is in the left tail of the distribution, we use z

0.95

= −z

0.05

In the table we read P(Z ≥ 1.64) = 0.0505 and P(Z ≥ 1.65) = 0.0495, from

which we conclude z

0.05

≈ (1.64 + 1.65)/2=1.645 and z

0.95

≈−1.645.

23.5 In Table B.1 we ﬁnd P(T

≥ 4.541) = 0.01, so t

3,0.01

=4.541. For

35,0.9975

, we need to use t

35,0.9975

= −t

35,0.0025

. In the table we ﬁnd t

30,0.0025

3.030 and t

40,0.0025

=2.971, and by interpolation t

35,0.0025

≈ (3.030 +

2.971)/2=3.0005. Hence, t

35,0.9975

≈−3.000.

23.6 The order statistics are estimates for c

∗

0.025

and c

∗

0.975

, respectively. So

the corresponding α is 0.05, and the 95% bootstrap conﬁdence interval for µ

is:



656.88 −1.713

1037.3

√

135

, 656.88 − (−2.443)

1037.3

√

135



= (504.0, 875.0).

23.6 Exercises

23.1  A bottling machine is known to ﬁll wine bottles with amounts that

follow an N (µ, σ

) distribution, with σ = 5 (ml). In a sample of 16 bottles,

¯x = 743 (ml) was found. Construct a 95% conﬁdence interval for µ.

23.2  You are given a dataset that may be considered a realization of a

normal random sample. The size of the dataset is 34, the average is 3.54, and

the sample standard deviation is 0.13. Construct a 98% conﬁdence interval

for the unknown expectation µ.

23.3 You have ordered 10 bags of cement, which are supposed to weigh 94 kg

each. The average weight of the 10 bags is 93.5 kg. Assuming that the 10

weights can be viewed as a realization of a random sample from a normal

distribution with unknown parameters, construct a 95% conﬁdence interval

for the expected weight of a bag. The sample standard deviation of the 10

weightsis0.75.

23.4 A new type of car tire is launched by a tire manufacturer. The auto-

mobile association performs a durability test on a random sample of 18 of

these tires. For each tire the durability is expressed as a percentage: a score

of 100 (%) means that the tire lasted exactly as long as the average standard

tire, an accepted comparison standard. From the multitude of factors that in-

ﬂuence the durability of individual tires the assumption is warranted that the

durability of an arbitrary tire follows an N(µ, σ

) distribution. The parame-

ters µ and σ

characterize the tire type,andµ could be called the durability

index for this type of tire. The automobile association found for the tested

tires: ¯x

= 195.3ands

=16.7. Construct a 95% conﬁdence interval for µ.

23.6 Exercises 357

23.5  During the 2002 Winter Olympic Games in Salt Lake City a newspaper

article mentioned the alleged advantage speed-skaters have in the 1500 m race

if they start in the outer lane. In the men’s 1500 m, there were 24 races, but

in race 13 (really!) someone fell and did not ﬁnish. The results in seconds of

the remaining 23 races are listed in Table 23.5. You should know that who

races against whom, in which race, and who starts in the outer lane are all

determined by a fair lottery.

Table 23.5. Speed-skating results in seconds, men’s 1500 m (except race 13), 2002

Winter Olympic Games.

Race Inner Outer Diﬀerence

number lane lane

1 107.04 105.98 1.06

2 109.24 108.20 1.04

3 111.02 108.40 2.62

4 108.02 108.58 −0.56

5 107.83 105.51 2.32

6 109.50 112.01 − 2.51

7 111.81 112.87 − 1.06

8 111.02 106.40 4.62

9 106.04 104.57 1.47

10 110.15 110.70 −0.55

11 109.42 109.45 −0.03

12 108.13 109.57 −1.44

14 105.86 105.97 −0.11

15 108.27 105.63 2.64

16 107.63 105.41 2.22

17 107.72 110.26 −2.54

18 106.38 105.82 0.56

19 107.78 106.29 1.49

20 108.57 107.26 1.31

21 106.99 103.95 3.04

22 107.21 106.00 1.21

23 105.34 105.26 0.08

24 108.76 106.75 2.01

Mean 108.25 107.43 0.82

St.dev. 1.70 2.42 1.78

a. As a consequence of the lottery and the fact that many diﬀerent factors

contribute to the actual time diﬀerence “inner lane minus outer lane” the

assumption of a normal distribution for the diﬀerence is warranted. The

numbers in the last column can be seen as realizations from an N (δ, σ

)

358 23 Conﬁdence intervals for the mean

distribution, where δ is the expected outer lane advantage. Construct a

95% conﬁdence interval for δ.N.B.n = 23, not 24!

b. You decide to make a bootstrap conﬁdence interval instead. Describe the

appropriate bootstrap experiment.

c. The bootstrap experiment was performed with one thousand repetitions.

Part of the bootstrap outcomes are listed in the following table. From the

ordered list of results, numbers 21 to 60 and 941 to 980 are given. Use

these to construct a 95% bootstrap conﬁdence interval for δ.

21–25 −2.202 −2.164 −2.111 −2.109 −2.101

26–30 −2.099 −2.006 −1.985 −1.967 −1.929

31–35 −1.917 −1.898 −1.864 −1.830 −1.808

36–40 −1.800 −1.799 −1.774 −1.773 −1.756

41–45 −1.736 −1.732 −1.731 −1.717

−1.716

46–50 −1.699 −1.692 −1.691 −1.683 −1.666

51–55 −1.661 −1.644 −1.638 −1.637 −1.620

56–60 −1.611 −1.611 −1.601 −1.600 −1.593

941–945 1.648 1.667 1.669 1.689 1.696

946–950 1.708 1.722 1.726 1.735 1.814

951–955 1.816 1.825 1.856 1.862 1.864

956–960 1.875 1.877 1.897 1.905 1.917

961–965 1.923 1.948 1.961 1.987 2.001

966–970 2.015 2.015 2.017 2.018 2.034

971–975 2.035 2.037 2.039 2.053 2.060

976–980 2.088 2.092 2.101 2.129 2.143

23.6  A dataset x

,...,x

is given, modeled as realization of a sam-

ple X

, X

,...,X

from an N(µ, 1) distribution. Suppose there are sample

statistics L

= g(X

,...,X

)andU

= h(X

,...,X

) such that

P(L

<µ<U

)=0.95

for every value of µ. Suppose that the corresponding 95% conﬁdence interval

derived from the data is (l

)=(−2, 5).

a. Suppose θ =3µ +7. Let

=3L

+7 and

=3U

+ 7. Show that



<θ<



=0.95.

b. Write the 95% conﬁdence interval for θ in terms of l

and u

c. Suppose θ =1− µ. Again, ﬁnd

and

, as well as the conﬁdence

interval for θ.

d. Suppose θ = µ

. Can you construct a conﬁdence interval for θ?

23.6 Exercises 359

23.7  A 95% conﬁdence interval for the parameter µ of a Pois(µ) distri-

bution is given: (2, 3). Let X be a random variable with this distribution.

Construct a 95% conﬁdence interval for P(X =0)=e

−µ

23.8 Suppose that in Exercise 23.1 the content of the bottles has to be de-

termined by weighing. It is known that the wine bottles involved weigh on

average 250 grams, with a standard deviation of 15 grams, and the weights

follow a normal distribution. For a sample of 16 bottles, an average weight of

998 grams was found. You may assume that 1 ml of wine weighs 1 gram, and

that the ﬁlling amount is independent of the bottle weight. Construct a 95%

conﬁdence interval for the expected amount of wine per bottle, µ.

23.9 Consider the alpha-particle counts discussed in Section 23.4; the data

are given in Table 23.4. We want to bootstrap in order to make a bootstrap

conﬁdence interval for the expected number of particles in a 7.5-second inter-

val.

a. Describe in detail how you would perform the bootstrap simulation.

b. The bootstrap experiment was performed with one thousand repetitions.

Part of the (ordered) bootstrap t

∗

’s are given in the following table. Con-

struct the 95% bootstrap conﬁdence interval for the expected number of

particles in a 7.5-second interval.

1–5 −2.996 − 2.942 −2.831 − 2.663 −2.570

6–10 −2.537 −2.505 −2.290 −2.273 −2.228

11–15 −2.193 −2.112 −2.092 − 2.086 −2.045

16–20 −1.983 −1.980 −1.978 − 1.950 −1.931

21–25 −1.920 −1.910 −1.893 − 1.889

−1.888

26–30 −1.865 −1.864 −1.832 − 1.817 −1.815

31–35 −1.755 −1.751 −1.749 − 1.746 −1.744

36–40 −1.734 −1.723 −1.710 − 1.708 −1.705

41–45 −1.703 −1.700 −1.696 − 1.692 −1.691

46–50 −1.691 −1.675 −1.660

−1.656 − 1.650

951–955 1.635 1.638 1.643 1.648 1.661

956–960 1.666 1.668 1.678 1.681 1.686

961–965 1.692 1.719 1.721 1.753 1.772

966–970 1.773 1.777 1.806 1.814 1.821

971–975 1.824 1.826 1.837 1.838 1.845

976–980 1.862 1.877 1.881 1.883 1.956

981–985 1.971 1.992 2.060 2.063 2.083

986–990 2.089 2.177 2.181 2.186 2.224

991–995 2.234 2.264 2.273 2.310 2.348

996–1000 2.

483 2.556 2.870 2.890 3.546

360 23 Conﬁdence intervals for the mean

c. Answer this without doing any calculations: if we made the 98% boot-

strap conﬁdence interval, would it be smaller or larger than the interval

constructed in Section 23.4?

23.10 In a report you encounter a 95% conﬁdence interval (1.6, 7.8) for the

parameter µ of an N(µ, σ

) distribution. The interval is based on 16 observa-

tions, constructed according to the studentized mean procedure.

a. What is the mean of the (unknown) dataset?

b. You prefer to have a 99% conﬁdence interval for µ.Constructit.

23.11  A 95% conﬁdence interval for the unknown expectation of some

distribution contains the number 0.

a. We construct the corresponding 98% conﬁdence interval, using the same

data. Will it contain the number 0?

b. The conﬁdence interval in fact is a bootstrap conﬁdence interval. We re-

peat the bootstrap experiment (using the same data) and construct a new

95% conﬁdence interval based on the results. Will it contain the number 0?

c. We collect new data, resulting in a dataset of the same size. With this data,

we construct a 95% conﬁdence interval for the unknown expectation. Will

the interval contain 0?

23.12 Let Z

,...,Z

be a random sample from an N(0, 1) distribution. Deﬁne

= µ+σZ

for i =1,...,nand σ>0. Let

X denote the sample averages

and S

the sample standard deviations, of the Z

and X

, respectively.

a. Show that X

,...,X

is a random sample from an N(µ, σ

) distribution.

b. Express

X and S

in terms of

Z, S

, µ,andσ.

c. Verify that

X − µ

√

and explain why this shows that the distribution of the studentized mean

does not depend on µ and σ.

More on conﬁdence intervals

While in Chapter 23 we were solely concerned with conﬁdence intervals for

expectations, in this chapter we treat a variety of topics. First, we focus on

conﬁdence intervals for the parameter p of the binomial distribution. Then,

based on an example, we brieﬂy discuss a general method to construct conﬁ-

dence intervals. One-sided conﬁdence intervals, or upper and lower conﬁdence

bounds, are discussed next. At the end of the chapter we investigate the ques-

tion of how to determine the sample size when a conﬁdence interval of a certain

width is desired.

24.1 The probability of success

A common situation is that we observe a random variable X with a Bin (n, p)

distribution and use X to estimate p. For example, if we want to estimate

the proportion of voters that support candidate G in an election, we take a

sample from the voter population and determine the proportion in the sample

that supports G.Ifn individuals are selected at random from the population,

where a proportion p supports candidate G, the number of supporters X in

the sample is modeled by a Bin (n, p) distribution; we count the supporters of

candidate G as “successes.” Usually, the sample proportion X/n is taken as

an estimator for p.

If we want to make a conﬁdence interval for p, based on the number of suc-

cesses X in the sample, we need to ﬁnd statistics L and U (see the deﬁnition

of conﬁdence intervals on page 343) such that

P(L<p<U)=1− α,

where L and U are to be based on X only. In general, this problem does

not have a solution. However, the method for large n described next, some-

times called “the Wilson method” (see [40]), yields conﬁdence intervals with

362 24 More on conﬁdence intervals

conﬁdence level approximately 100(1 − α)%. (How close the true conﬁdence

level is to 100(1 −α)% depends on the (unknown) p, though it is known that

for p near 0 and 1 it is too low. For some details and an alternative for this

situation, see Remark 24.1.)

Recall the normal approximation to the binomial distribution, a consequence

of the central limit theorem (see page 201 and Exercise 14.5): for large n,the

distribution of X is approximately normal and

X − np



np(1 − p)

is approximately standard normal. By dividing by n in both the numerator

and the denominator, we see that this equals:

− p



p(1−p)

Therefore, for large n

⎛

⎝

−z

α/2

− p



p(1−p)

α/2

⎞

⎠

≈ 1 − α.

Note that the event

−z

α/2

− p



p(1−p)

α/2

is the same as

⎛

⎝

− p



p(1−p)

⎞

⎠



α/2





− p



−



α/2



p(1 − p)

< 0.

To derive expressions for L and U we can rewrite the inequality in this state-

ment to obtain the form L<p<U, but the resulting formulas are rather

awkward. To obtain the conﬁdence interval, we instead substitute the data

values directly and then solve for p, which yields the desired result.

Suppose, in a sample of 125 voters, 78 support one candidate. What is the 95%

conﬁdence interval for the population proportion p supporting that candidate?

The realization of X is x =78andn = 125. We substitute this, together with

α/2

= z

0.025

=1.96, in the last inequality:



125

− p



−

(1.96)

125

p(1 − p) < 0,

24.1 The probability of success 363

0.4 0.80.54 0.70

−0.01

0.00

0.01

0.02

0.03

0.04

0.05

...

.....

...............

....

...

.....................................................................................................

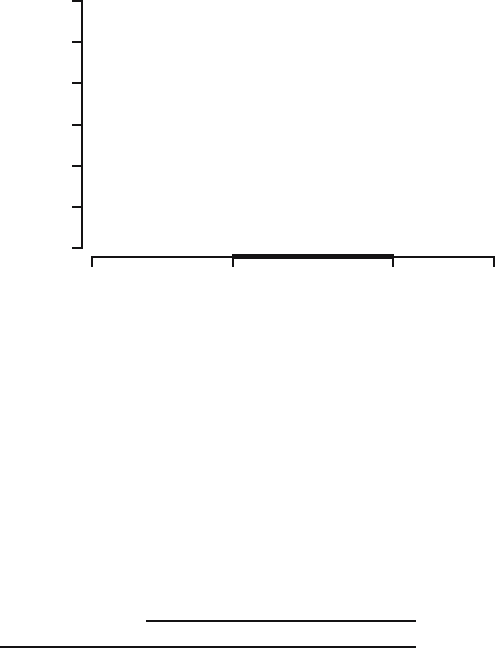
Fig. 24.1. The parabola 1.0307 p

− 1.2787 p +0.3894 and the resulting conﬁdence

interval.

or, working out squares and products and grouping terms:

1.0307 p

− 1.2787 p +0.3894 < 0.

This quadratic form describes a parabola, which is depicted in Figure 24.1.

Also, for other values of n and x there always results a quadratic inequality like

this, with a positive coeﬃcient for p

and a similar picture. For the conﬁdence

interval we need to ﬁnd the values where the parabola intersects the horizontal

axis. The solutions we ﬁnd are:

1,2

−(−1.2787) ±



(−1.2787)

− 4 · 1.0307 · 0.3894

2 · 1.0307

=0.6203 ± 0.0835;

hence, l =0.54 and u =0.70, so the resulting conﬁdence interval is (0.54, 0.70).

Quick exercise 24.1 Suppose in another election we ﬁnd 80 supporters in a

sample of 200. Suppose we use α =0.0456 for which z

α/2

=2.Constructthe

corresponding conﬁdence interval for p.

Remark 24.1 (Coverage probabilities and an alternative method).

Because of the discrete nature of the binomial distribution, the probabil-

ity that the conﬁdence interval covers the true parameter value depends

on p. As a function of p it typically oscillates in a sawtooth-like manner

around 1 − α, being too high for some values and too low for others. This

is something that cannot be escaped from; the phenomenon is present in

every method. In an average sense, the method treated in the text yields

coverage probabilities close to 1 −α, though for arbitrarily high values of n

it is possible to ﬁnd p’s for which the actual coverage is several percentage

points too low. The low coverage occurs for p’s near 0 and 1.

364 24 More on conﬁdence intervals

An alternative is the method proposed by Agresti and Coull, which overall

is more conservative than the Wilson method (in fact, the Agresti-Coull

interval contains the Wilson interval as a proper subset). Especially for p

near 0 or 1 this method yields conservative conﬁdence intervals. Deﬁne

X = X +

α/2

)

and ˜n = n +(z

α/2

)

and ˜p =

X/˜n. The approximate 100(1 − α)% conﬁdence interval is then

given by



˜p − z

α/2



˜p(1 − ˜p)

˜n

, ˜p + z

α/2



˜p(1 − ˜p)

˜n



For a clear survey paper on conﬁdence intervals for p we recommend Brown

et al. [4].

24.2 Is there a general method?

We have now seen a number of examples of conﬁdence intervals, and while it

should be clear to you that in each of these cases the resulting intervals are

valid conﬁdence intervals, you may wonder how we go about ﬁnding conﬁdence

intervals in new situations. One could ask: is there a general method? We ﬁrst

consider an example.

A conﬁdence interval for the minimum lifetime

Suppose we have a random sample X

,...,X

from a shifted exponential

distribution, that is, X

= δ + Y

,whereY

,...,Y

are a random sample from

an Exp (1) distribution. This type of random variable is sometimes used to

model lifetimes; a minimum lifetime is guaranteed, but otherwise the lifetime

has an exponential distribution. The unknown parameter δ represents the

minimum lifetime, and the probability density of the X

is positive only for

values greater than δ.

To derive information about δ it is natural to use the smallest observed value

T =min{ X

,...,X

}. This is also the maximum likelihood estimator for δ;

see Exercise 21.6. Writing

T =min{δ + Y

,...,δ+ Y

} = δ +min{Y

,...,Y

}

and observing that M =min{Y

,...,Y

} has an Exp (n) distribution (see

Exercise 8.18), we ﬁnd for the distribution function of T : F

(a)=0fora<δ

and

(a)=P(T ≤ a)=P(δ + M ≤ a)=P(M ≤ a − δ)

=1−e

−n(a−δ)

for a ≥ δ.

(24.1)

Next, we solve

24.2 Is there a general method? 365

P(c

<T <c

)=1− α

by requiring

P(T ≤ c

)=P(T ≥ c

α.

Using (24.1) we ﬁnd the following equations:

1 − e

−n(c

−δ)

α and e

−n(c

−δ)

whose solutions are

= δ −



1 −



and c

= δ −





Both c

and c

are values larger than δ, because the logarithms are negative.

We have found that, whatever the value of δ:



δ −



1 −



<T <δ−







=1−α.

By rearranging the inequalities, we see this is equivalent to



T +





<δ<T+



1 −





=1−α,

and therefore a 100(1 − α)% conﬁdence interval for δ is given by



t +





,t+



1 −





. (24.2)

For α =0.05 this becomes:



t −

3.69

,t−

0.0253



Quick exercise 24.2 Suppose you have a dataset of size 15 from a shifted

Exp(1) distribution, whose minimum value is 23.5. What is the 99% conﬁdence

interval for δ?

Looking back at the example, we see that the conﬁdence interval could be

constructed because we know that T −δ = M has an exponential distribution.

There are many more examples of this type: some function g(T,θ)ofasample

statistic T and the unknown parameter θ has a known distribution. However,

this still does not cover all the ways to construct conﬁdence intervals (see also

the following remark).

Remark 24.2 (About a general method). Suppose X

,...,X

is a

random sample from some distribution depending on some unknown pa-

rameter θ and let T be a sample statistic. One possible choice is to select

a T that is an estimator for θ, but this is not necessary. In each case, the

A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )

Подождите немного. Документ загружается.