A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику

Подождите немного. Документ загружается.

25.3 Type I and type II errors 377

P(T ≤ 61). In other situations, the direction in which values of T provide

stronger evidence against H

may be to the right of the observed value t,

in which case one would compute a right tail probability P(T ≥ t). In both

cases the tail probability expresses how likely it is to obtain a value of the

test statistic T at least as extreme as the value t observed for the data. Such

a probability is called a p-value.Inaway,thesizeofthep-value reﬂects how

much evidence the observed value t provides against H

.Thesmaller the

p-value, the stronger evidence the observed value t bears against H

The phrase “at least as extreme as the observed value t” refers to a particular

direction, namely the direction in which values of T provide stronger evidence

against H

and in favor of H

. In our example, this was to the left of 61, and

the p-value corresponding to 61 was P(T ≤ 61) = 0.00014. In this case it is

clear what is meant by “at least as extreme as t” and which tail probability

corresponds to the p-value. However, in some testing problems one can deviate

from H

in both directions. In such cases it may not be clear what values of

T are at least as extreme as the observed value, and it may be unclear how

the p-value should be computed. One approach to a solution in this case is

to simply compute the one-tailed p-value that corresponds to the direction in

which t deviates from H

Quick exercise 25.3 Suppose that the Allied intelligence agencies had re-

ported a production of 80 tanks, so that we would test H

: N = 80 against

: N<80. Compute the p-value corresponding to 61. Would you conclude

is false beyond reasonable doubt?

25.3 Type I and type II errors

Suppose that the maximum is 200 instead of 61. This is also to the left of

the expected value 292.5 of T . Is it far enough to the left to reject the null

hypothesis? In this case the p-value is equal to

P(T ≤ 200) = P(max{X

,...,X

}≤200)

200

350

199

349

···

196

346

=0.0596.

This means that if the total number of produced tanks is 350, then in 5.96%

of all cases we would observe a value of T that is at least as extreme as the

value 200. Before we decide whether 0.0596 is small enough to reject the null

hypothesis let us explore in more detail what the preceding probability stands

for.

It is important to distinguish between (1) the true state of nature: H

is true

or H

is true and (2) our decision: we reject or do not reject H

on the basis

of the data. In our example the possibilities for the true state of nature are:

Ĺ H

is true, i.e., there are 350 tanks produced.

Ĺ H

is true, i.e., the number of tanks produced is less than 350.

378 25 Testing hypotheses: essentials

We do not know in which situation we are. There are two possible decisions:

Ĺ We reject H

in favor of H

Ĺ We do not reject H

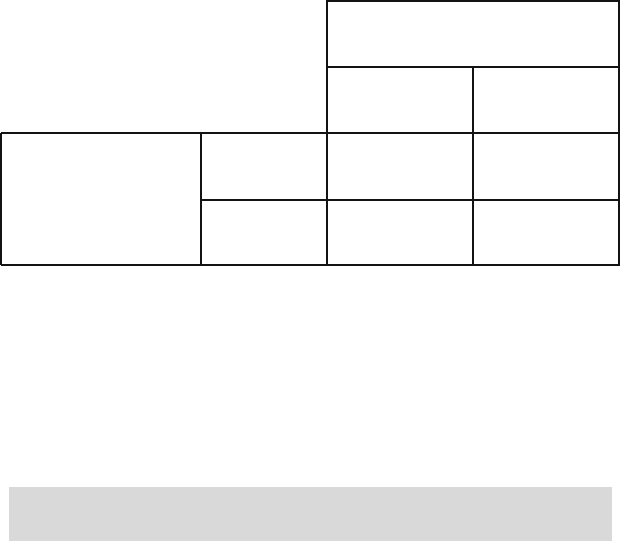
This leads to four possible situations, which are summarized in Figure 25.2.

True state of nature

is true H

is true

Reject H

Type I error Correct decision

Our decision on the

basis of the data

Not reject H

Correct decision Type II error

Fig. 25.2. Four situations when deciding about H

There are two situations in which the decision made on the basis of the data is

wrong. The null hypothesis H

may be true, whereas the data lead to rejection

of H

. On the other hand, the alternative hypothesis H

may be true, whereas

we do not reject H

on the basis of the data. These wrong decisions are called

type I and type II errors.

Type I and II errors. A type I error occurs if we falsely reject

.Atype II error occurs if we falsely do not reject H

In courtroom terminology, a type I error corresponds to convicting an innocent

defendant, whereas a type II error corresponds to acquitting a criminal.

If H

: N = 350 is true, then the decision to reject H

is a type I error. We

will never know whether we make a type I error. However, given a particular

decision rule, we can say something about the probability of committing a

type I error. Suppose the decision rule would be “reject H

: N = 350 when-

ever T ≤ 200.” With this decision rule the probability of committing a type I

error is P(T ≤ 200) = 0.0596. If we are willing to run the risk of committing

a type I error with probability 0.0596, we could adopt this decision rule. This

would also mean that on the basis of an observed maximum of 200 we would

reject H

in favor of H

: N<350.

Quick exercise 25.4 Suppose we adopt the following decision rule about the

null hypothesis: “reject H

: N = 350 whenever T ≤ 250.” Using this decision

rule, what is the probability of committing a type I error?

25.4 Solutions to the quick exercises 379

The question remains what amount of risk one is willing to take to falsely

reject H

, or in courtroom terminology: how small should the p-value be to

reach a conclusion that is “beyond reasonable doubt”? In many situations,

as a rule of thumb 0.05 is used as the level where reasonable doubt begins.

Something happening with probability less than or equal to 0.05 is then viewed

as being too exceptional. However, there is no general rule that speciﬁes how

small the p-value must be to reject H

. There is no way to argue that this

probability should be below 0.10 or 0.18 or 0.009—or anything else.

A possible solution is to solely report the p-value corresponding to the ob-

served value of the test statistic. This is objective and does not have the

arbitrariness of a preselected level such as 0.05. An investigator who reports

the p-value conveys the maximum amount of information contained in the

dataset and permits all decision makers to choose their own level and make

their own decision about the null hypothesis. This is especially important

when there is no justiﬁable reason for preselecting a particular value for such

a level.

25.4 Solutions to the quick exercises

25.1 One is interested in whether dry drilling is faster than wet drilling.

Hence if we reject H

: µ

= µ

, we would like to conclude that the drill time

is smaller for dry drilling than for wet drilling. Since µ

and µ

represent the

drill time for dry and wet drilling, we should choose H

: µ

<µ

25.2 The value of

is at least 3 and if we ﬁnd a value of

that is larger

than 348, then at least one of the ﬁve numbers must be greater than 350, so

that we immediately know that H

as well as H

is false. Hence the possible

values of

that are relevant for our testing problem are between 3 and 348.

We know from Section 20.1 that 2

− 1isanunbiasedestimatorforN ,

no matter what the value of N is. This implies that values of

itself are

centered around (N +1)/2. Hence values close to 351/2=175.5 are in favor

of H

, whereas values close to 3 are in favor of H

. Values close to 348 are

against H

, but also against H

. See Figure 25.3.

3 175.5 348

Values in

favor of H

Values in

favor of H

Values against

both H

and H

Fig. 25.3. Values of the test statistic

25.3 The p-value corresponding to 61 is now equal to

P(T ≤ 61) =

···

=0.2475.

380 25 Testing hypotheses: essentials

If H

is true, then in 24.75% of the time one will observe a value T less than

or equal to 61. Such values are not exceptionally small for T under H

,and

therefore the evidence that the value 61 bears against H

is pretty weak. We

cannot reject H

beyond reasonable doubt.

25.4 The type I error associated with the decision rule occurs if N = 350

is true) and t ≤ 250 (reject H

). The probability that this happens is

P(T ≤ 250) =

250

350

249

349

···

246

346

=0.1838.

25.5 Exercises

25.1 In a study about train delays in The Netherlands one was interested in

whether arrival delays of trains exhibit more variation during rush hours than

during quiet hours. The observed arrival delays during rush hours are mod-

eled as realizations of a random sample from a distribution with variance σ

and similarly the observed arrival delays during quiet hours correspond to a

distribution with variance σ

. One tests the null hypothesis H

: σ

= σ

What do you choose as the alternative hypothesis?

25.2  On average, the number of babies born in Cleveland, Ohio, in the

month of September is 1472. On January 26, 1977, the city was immobilized

by a blizzard. Nine months later, in September 1977, the recorded number of

births was 1718. Can the increase of 246 be attributed to chance? To inves-

tigate this, the number of births in the month of September is modeled by a

Poisson random variable with parameter µ,andwetestH

: µ = 1472. What

would you choose as the alternative hypothesis?

25.3 Recall Exercise 17.9 about black cherry trees. The scatterplot of y (vol-

ume) versus x = d

h (squared diameter times height) seems to indicate that

the regression line y = α + βx runs through the origin. One wants to inves-

tigate whether this is true by means of a testing problem. Formulate a null

hypothesis and alternative hypothesis in terms of (one of) the parameters α

and β.

25.4  Consider the example from Section 4.4 about the number of cycles

up to pregnancy of smoking and nonsmoking women. Suppose the observed

number of cycles are modeled as realizations of random samples from geo-

metric distributions. Let p

be the parameter of the geometric distribution

corresponding to smoking women and p

be the parameter for the nonsmok-

ing women. We are interested in whether p

is diﬀerent from p

,andwe

investigate this by testing H

: p

= p

against H

: p

= p

a. If the data are as given in Exercise 17.5, what would you choose as a test

statistic?

25.5 Exercises 381

b. What would you choose as a test statistic, if you were given the extra

knowledge as in Table 21.1?

c. Suppose we are interested in whether smoking women are less likely to get

pregnant than nonsmoking women. What is the appropriate alternative

hypothesis in this case?

25.5  Suppose a dataset is a realization of a random sample X

,...,X

from a uniform distribution on [0,θ], for some (unknown) θ>0. We test

: θ =5versusH

: θ =5.

a. We take T

=max{X

,...,X

} as our test statistic. Specify what

the (relevant) possible values are for T and which are in favor of H

and

which are in favor of H

. For instance, make a picture like Figure 25.1.

b. Same as a, but now for test statistic T

= |2

− 5|.

25.6  To test a certain null hypothesis H

one uses a test statistic T with

a continuous sampling distribution. One agrees that H

is rejected if one

observes a value t of the test statistic for which (under H

) the right tail

probability P(T ≥ t) is smaller than or equal to 0.05. Given below are diﬀerent

values t and a corresponding left or right tail probability (under H

). Specify

for each case what the p-value is, if possible, and whether we should reject H

a. t =2.34 and P(T ≥ 2.34) = 0.23.

b. t =2.34 and P(T ≤ 2.34) = 0.23.

c. t =0.03 and P(T ≥ 0.03) = 0.968.

d. t =1.07 and P(T ≤ 1.07) = 0.981.

e. t =1.07 and P(T ≤ 2.34) = 0.01.

f. t =2.34 and P(T ≤ 1.07) = 0.981.

g. t =2.34 and P(T ≤ 1.07) = 0.800.

25.7 (Exercise 25.2 continued). The number of births in September is mod-

eled by a Poisson random variable T with parameter µ, which represents the

expected number of births. Suppose that one uses T to test the null hypothe-

sis H

: µ = 1472 and that one decides to reject H

on the basis of observing

the value t = 1718.

a. In which direction do values of T provide evidence against H

(and in

favor of H

b. Compute the p-value corresponding to t = 1718, where you may use the

fact that the distribution of T can be approximated by an N(µ, µ) distri-

bution.

25.8 Suppose we want to test the null hypothesis that our dataset is a realiza-

tion of a random sample from a standard normal distribution. As test statistic

we use the Kolmogorov-Smirnov distance between the empirical distribution

382 25 Testing hypotheses: essentials

function F

of the data and the distribution function Φ of the standard nor-

mal:

T =sup

a∈R

(a) − Φ(a)|.

What are the possible values of T andinwhichdirectiondovaluesofT deviate

from the null hypothesis?

25.9 Recall the example from Section 18.3, where we investigated whether the

software data are exponential by means of the Kolmogorov-Smirnov distance

between the empirical distribution function F

of the data and the estimated

exponential distribution function:

=sup

a∈R

(a) − (1 − e

−

Λa

)|.

For the data we found t

=0.176. By means of a new parametric bootstrap

we simulated 100 000 realizations of T

and found that all of them are smaller

than 0.176. What can you say about the p-value corresponding to 0.176?

25.10  Consider the coal data from Table 23.1, where 23 gross caloriﬁc value

measurements are listed for Osterfeld coal coded 262DE27. We modeled this

dataset as a realization of a random sample from a normal distribution with

expectation µ unknown and standard deviation 0.1 MJ/kg. We are planning

to buy a shipment if the gross caloriﬁc value exceeds 23.75 MJ/kg. In order

to decide whether this is sensible, we test the null hypothesis H

: µ =23.75

with test statistic

a. What would you choose as the alternative hypothesis?

b. For the dataset ¯x

is 23.788. Compute the corresponding p-value, using

that

has an N(23.75, (0.1)

/23) distribution under the null hypothesis.

25.11  One is given a number t, which is the realization of a random vari-

able T with an N (µ, 1) distribution. To test H

: µ = 0 against H

: µ =0,

one uses T as the test statistic. One decides to reject H

in favor of H

|t|≥2. Compute the probability of committing a type I error.

Testing hypotheses: elaboration

In the previous chapter we introduced the setup for testing a null hypothesis

against an alternative hypothesis using a test statistic T . The notions of type I

error and type II error were introduced. A type I error occurs when we falsely

reject H

on the basis of the observed value of T , whereas a type II error

occurs when we falsely do not reject H

. The decision to reject H

or not was

basedonthesizeofthep-value. In this chapter we continue the introduction

of basic concepts of testing hypotheses, such as signiﬁcance level and critical

region, and investigate the probability of committing a type II error.

26.1 Signiﬁcance level

As mentioned in the previous chapter, there is no general rule that speciﬁes a

level below which the p-value is considered exceptionally small. However, there

are situations where this level is set apriori, and the question is: which values

of the test statistic should then lead to rejection of H

? To illustrate this, con-

sider the following example. The speed limit on freeways in The Netherlands

is 120 kilometers per hour. A device next to freeway A2 between Amsterdam

and Utrecht measures the speed of passing vehicles. Suppose that the device

is designed in such a way that it conducts three measurements of the speed

of a passing vehicle, modeled by a random sample X

. On the basis

of the value of the average

, the driver is either ﬁned for speeding or not.

For what values of

should we ﬁne the driver, if we allow that 5% of the

drivers are ﬁned unjustly?

Let us rephrase things in terms of a testing problem. Each measurement can

be thought of as

measurement = true speed + measurement error.

Suppose for the moment that the measuring device is carefully calibrated, so

that the measurement error is modeled by a random variable with mean zero

384 26 Testing hypotheses: elaboration

and known variance σ

,sayσ

= 4. Moreover, in physical experiments such as

this one, the measurement error is often modeled by a random variable with a

normal distribution. In that case, the measurements X

are modeled

by a random sample from an N(µ, 4) distribution, where the parameter µ

represents the true speed of the passing vehicle. Our testing problem can now

be formulated as testing

: µ = 120 against H

: µ>120,

with test statistic

T =

+ X

Since sums of independent normal random variables again have a normal dis-

tribution (see Remark 11.2), it follows that

has an N(µ, 4/3) distribution.

In particular, the distribution of T =

is centered around µ no matter what

the value of µ is. Values of T close to 120 are therefore in favor of H

.Valuesof

T that are far from 120 are considered as strong evidence against H

.Values

much larger than 120 suggest that µ>120 and are therefore in favor of H

Values much smaller than 120 suggest that µ<120. They also constitute

evidence against H

, but even stronger evidence against H

. Thus we reject

in favor of H

only for values of T larger than 120. See also Figure 26.1.

120

Values in

favor of H

Fig. 26.1. Possible values of T =

Rejection of H

in favor of H

corresponds to ﬁning the driver for speeding.

Unjustly ﬁning a driver corresponds to falsely rejecting H

, i.e., committing

a type I error. Since we allow 5% of the drivers to be ﬁned unjustly, we are

dealing with a testing problem where the probability of committing a type I

error is set a priori at 0.05. The question is: for which values of T should

we reject H

? The decision rule for rejecting H

should be such that the

corresponding probability of committing a type I error is 0.05. The value 0.05

is called the signiﬁcance level.

Significance level. The signiﬁcance level is the largest accept-

able probability of committing a type I error and is denoted by α,

where 0 <α<1.

We speak of “performing the test at level α,” as well as “rejecting H

favor of H

at level α.” In our example we are testing H

: µ = 120 against

: µ>120 at level 0.05.

26.1 Signiﬁcance level 385

Quick exercise 26.1 Suppose that in the freeway example H

: µ = 120 is

rejected in favor of H

: µ>120 at level α =0.05. Will it necessarily be

rejected at level α =0.01? On the other hand, suppose that H

: µ = 120

is rejected in favor of H

: µ>120 at level α =0.01. Will it necessarily be

rejected at level α =0.05?

Let us continue with our example and determine for which values of T =

we should reject H

at level α =0.05 in favor of H

: µ>120. Suppose

we decide to ﬁne each driver whose recorded average speed is 121 or more,

i.e., we reject H

whenever T ≥ 121. Then how large is the probability of a

type I error P(T ≥ 121)? When H

: µ = 120 is true, then T =

has an

N(120, 4/3) distribution, so that by the change-of-units rule for the normal

distribution (see page 106), the random variable

Z =

T − 120

√

has an N(0, 1) distribution. This implies that

P(T ≥ 121) = P



T − 120

√

≥

121 − 120

√



=P(Z ≥ 0.87) .

From Table B.1, we ﬁnd P(Z ≥ 0.87) = 0.1922, which means that the prob-

ability of a type I error is greater than the signiﬁcance level α =0.05. Since

this level was deﬁned as the largest acceptable probability of a type I error,

we do not reject H

. Similarly, if we decide to reject H

whenever we record

an average of 122 or more, the probability of a type I error equals 0.0416

(check this). This is smaller than α =0.05, so in that case we reject H

.The

boundary case is the value c that satisﬁes P(T ≥ c)=0.05. To ﬁnd c,wemust

solve



Z ≥

c − 120

√



=0.05.

From Table B.2 we have that z

0.05

= t

∞,0.05

=1.645, so that we ﬁnd

c − 120

√

=1.645,

which leads to

c = 120 + 1.645 ·

√

= 121.9.

Hence, if we set the signiﬁcance level α at 0.05, we should reject H

: µ = 120

in favor of H

: µ>120 whenever T ≥ 121.9. For our freeway example this

means that if the average recorded speed of a passing vehicle is greater than

or equal to 121.9, then the driver is ﬁned for speeding. With this decision rule,

at most 5% of the drivers get ﬁned unjustly.

386 26 Testing hypotheses: elaboration

In connection with p-values: the signiﬁcance level is the level below which

the p-value is suﬃciently small to reject H

. Indeed, for any observed value

t ≥ 121.9 we reject H

,andthep-value for such a t is at most 0.05:

P(T ≥ t) ≤ P(T ≥ 121.9) = 0.05.

We will see more about this relation in the next section.

26.2 Critical region and critical values

In the freeway example the signiﬁcance level 0.05 corresponds to the decision

rule “reject H

: µ = 120 in favor H

: µ>120 whenever T ≥ 121.9.” The

set K = [121.9, ∞) consisting of values of the test statistic T for which we

reject H

is called critical region. The value 121.9, which is the boundary case

between rejecting and not rejecting H

, is called the critical value.

Critical region and critical values. Suppose we test H

against H

at signiﬁcance level α by means of a test statistic T .

The set K ⊂ R that corresponds to all values of T for which we

reject H

in favor of H

is called the critical region. Values on the

boundary of the critical region are called critical values.

The precise shape of the critical region depends on both the chosen signiﬁcance

level α and the test statistic T that is used. But it will always be such that

the probability that T ∈ K satisﬁes

P(T ∈ K) ≤ α in the case that H

is true.

At this point it becomes important to emphasize whether probabilities are

computed under the assumption that H

is true. With a slight abuse of nota-

tion, we brieﬂy write P(T ∈ K | H

) for the probability.

Relation with p-values

If we record average speed t = 124, then this value falls in the critical region

K = [121.9, ∞), so that H

: µ = 120 is rejected in favor H

: µ>120. On

the other hand we can also compute the p-value corresponding to the observed

value 124. Since values of T to the right provide stronger evidence against H

the p-value is the following right tail probability

P(T ≥ 124 | H

)=P



T − 120

√

≥

124 − 120

√



=P(Z ≥ 3.46) = 0.0003,

which is smaller than the signiﬁcance level 0.05. This is no coincidence.

A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )

Подождите немного. Документ загружается.