A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику

Подождите немного. Документ загружается.

17.6 Exercises 263

incorporated the 93 smokers and 474 nonsmokers, for which the exact number

of cycles was observed. Another analysis, based on the complete dataset, is

done in Section 21.1.

a. Consider the dataset x

,...,x

corresponding to the smoking women,

where x

denotes the number of cycles for the ith smoking woman. The

data are summarized in the following table.

Cycles 1 2 3 456789101112

Frequency291617439451 1 1 3

Source: C.R. Weinberg and B.C. Gladen. The beta-geometric distribution ap-

plied to comparative fecundability studies. Biometrics, 42(3):547–560, 1986.

The table lists the number of women that had to wait 1 cycle, 2 cycles,

etc. If we model the dataset as the realization of a random sample from a

geometric distribution with parameter p, then what would you choose as

an estimate for p?

b. Also estimate the parameter p for the 474 nonsmoking women, which

is also modeled as the realization of a random sample from a geometric

distribution. The dataset y

,...,y

474

,wherey

denotes the number of

cycles for the jth nonsmoking woman, is summarized here:

Cycles 1 2 3 4 5 6 789101112

Frequency19810755381822795 3 6 6

Source: C.R. Weinberg and B.C. Gladen. The beta-geometric distribution ap-

plied to comparative fecundability studies. Biometrics, 42(3):547–560, 1986.

You may use that y

+ y

+ ···+ y

474

= 1285.

c. Compare the estimates of the probability of becoming pregnant in three

or fewer cycles for smoking and nonsmoking women.

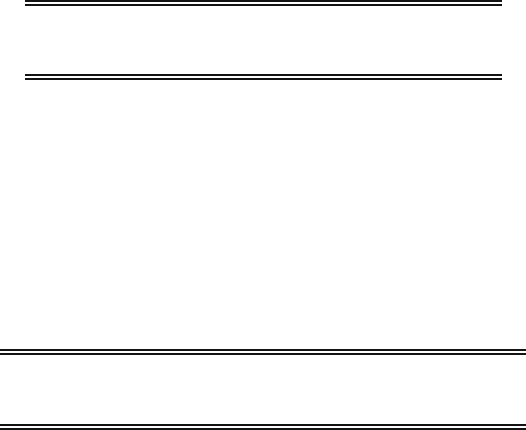
17.6 Recall Exercise 15.1 about the chest circumference of 5732 Scottish sol-

diers, where we constructed the histogram displayed in Figure 17.11. The

histogram suggests modeling the data as the realization of a random sample

from a normal distribution.

a. Suppose that for the dataset



= 228377.2and



= 9124064. What

would you choose as estimates for the parameters µ and σ of the N(µ, σ

)

distribution?

Hint: you may want to use the relation from Exercise 16.15.

b. Give an estimate for the probability that a Scottish soldier has a chest

circumference between 38.5 and 42.5 inches.

264 17 Basic statistical models

32 34 36 38 40 42 44 46 48 50

0.05

0.10

0.15

0.20

Fig. 17.11. Histogram of chest circumferences.

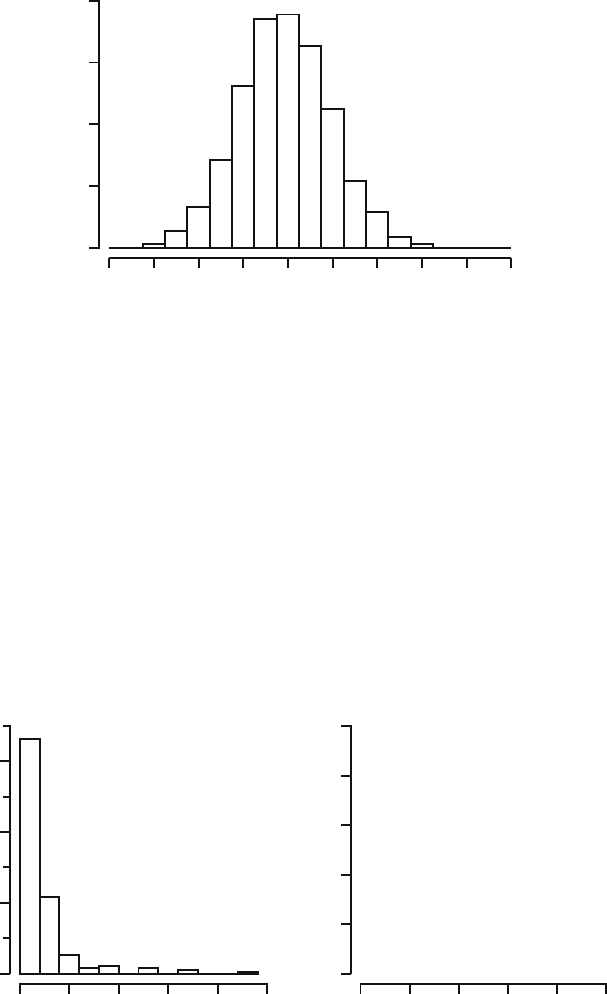
17.7  Recall Exercise 15.3 about time intervals between successive coal mine

disasters. Let us assume that the rate at which the disasters occur is constant

over time and that on a single day a disaster takes place with small probability

independently of what happens on other days. According to Chapter 12 this

suggests modeling the series of disasters with a Poisson process. Figure 17.12

displays a histogram and empirical distribution function of the observed time

intervals.

a. In the statistical model for this dataset we model the 190 time intervals

as the realization of a random sample. What would you choose for the

model distribution?

b. The sum of the observed time intervals is 40 549 days. Give an estimate

for the parameter(s) of the distribution chosen in part a.

0 500 1000 1500 2000 2500

0.001

0.002

0.003

0 500 1000 1500 2000 2500

0.0

0.2

0.4

0.6

0.8

1.0

...

....

...

....

.........

...

..........

........

...

......

..........

................................

..............

......

............

......................

.............................................................................

.............

.................

Fig. 17.12. Histogram of time intervals between successive disasters.

17.6 Exercises 265

17.8 The following data represent the number of revolutions to failure (in

millions) of 22 deep-groove ball-bearings.

17.88 28.92 33.00 41.52 42.12

45.60 48.48 51.84 51.96 54.12

55.56 67.80 68.64 68.88 84.12

93.12 98.64 105.12 105.84 127.92

128.04 173.40

Source: J. Lieblein and M. Zelen. Statistical investigation of the fatigue-life

of deep-groove ball-bearings. Journal of Research, National Bureau of Stan-

dards, 57:273–316, 1956; specimen worksheet on page 286.

Lieblein and Zelen propose modeling the dataset as a realization of a random

sample from a Weibull distribution, which has distribution function

F (x)=1− e

−(λx)

for x ≥ 0,

and F (x)=0,forx<0, where α, λ > 0.

a. Suppose that X is a random variable with a Weibull distribution. Check

that the random variable Y = X

has an exponential distribution with

parameter λ

and conclude that E[X

]=1/λ

b. Use part a to explain how one can use the data in the table to ﬁnd

an estimate for the parameter λ, if it is given that the parameter α is

estimated by 2.102.

17.9  The volume (i.e., the eﬀective wood production in cubic meters),

height (in meters), and diameter (in meters) (measured at 1.37 meter above

the ground) are recorded for 31 black cherry trees in the Allegheny National

Forest in Pennsylvania. The data are listed in Table 17.3. They were collected

to ﬁnd an estimate for the volume of a tree (and therefore for the timber

yield), given its height and diameter. For each tree the volume y and the

value of x = d

h are recorded, where d and h are the diameter and height

of the tree. The resulting points (x

),...,(x

) are displayed in the

scatterplot in Figure 17.13.

We model the data by the following linear regression model (without intercept)

= βx

+ U

for i =1, 2,...,31.

a. What physical reasons justify the linear relationship between y and d

Hint: how does the volume of a cylinder relate to its diameter and height?

b. We want to ﬁnd an estimate for the slope β of the line y = βx.Two

natural candidates are the average slope ¯z

,wherez

= y

,andthe

266 17 Basic statistical models

Table 17.3. Measurements on black cherry trees.

Diameter Height Volume

0.21 21.3 0.29

0.22 19.8 0.29

0.22 19.2 0.29

0.27 21.9 0.46

0.27 24.7 0.53

0.27 25.3 0.56

0.28 20.1 0.44

0.28 22.9 0.52

0.28 24.4 0.64

0.28 22.9 0.56

0.29 24.1 0.69

0.29 23.2 0.59

0.29 23.2 0.61

0.30 21.0 0.60

0.30 22.9 0.54

0.33 22.6 0.63

0.33 25.9 0.96

0.34 26.2 0.78

0.35 21.6 0.73

0.35 19.5 0.71

0.36 23.8 0.98

0.36 24.4 0.90

0.37 22.6 1.03

0.41 21.9 1.08

0.41 23.5 1.21

0.44 24.7 1.57

0.44 25.0 1.58

0.45 24.4 1.65

0.46 24.4 1.46

0.46 24.4 1.44

0.52 26.5 2.18

Source: A.C. Atkinson. Regression diagnostics, trend formations and con-

structed variables (with discussion). JournaloftheRoyalStatisticalSociety,

Series B, 44:1–36, 1982.

slope of the averages ¯y/¯x. In Chapter 22 we will encounter the so-called

least squares estimate:



i=1



i=1

17.6 Exercises 267

02468

0.0

0.5

1.0

1.5

2.0

2.5

··

Fig. 17.13. Scatterplot of the black cherry tree data.

Compute all three estimates for the data in Table 17.3. You need at least

5 digits accuracy, and you may use that



=87.456,



=26.486,



=9.369,



=95.498, and



= 314.644.

17.10 Let X be a random variable with (continuous) distribution function F .

Let m = q

0.5

= F

inv

(0.5) be the median of F and deﬁne the random variable

Y = |X − m|.

a. Show that Y has distribution function G, deﬁned by

G(y)=F (m + y) − F (m − y).

b. The MAD of F is the median of G. Show that if the density f correspond-

ing to F is symmetric around its median m,then

G(y)=2F (m + y) − 1

and derive that

inv

(

)=F

inv

(

) − F

inv

(

c. Use b to conclude that the MAD of an N(µ, σ

) distribution is equal to

σΦ

inv

(3/4), where Φ is the distribution function of a standard normal

distribution. Recall that the distribution function F of an N (µ, σ

)can

be written as

F (x)=Φ



x − µ



You might check that, as stated in Section 17.2, the MAD of the N (5, 4)

distribution is equal to 2Φ

inv

(3/4) = 1.3490.

268 17 Basic statistical models

17.11 In this exercise we compute the MAD of the Exp (λ) distribution.

a. Let X have an Exp(λ) distribution, with median m =(ln2)/λ. Show that

Y = |X − m| has distribution function

G(y)=



λy

− e

−λy



b. Argue that the MAD of the Exp(λ) distribution is a solution of the equa-

tion e

2λy

− e

λy

− 1=0.

c. Compute the MAD of the Exp(λ) distribution.

Hint: put x =e

λy

and ﬁrst solve for x.

The bootstrap

In the forthcoming chapters we will develop statistical methods to infer knowl-

edge about the model distribution and encounter several sample statistics to

do this. In the previous chapter we have seen examples of sample statistics

that can be used to estimate diﬀerent model features, for instance, the em-

pirical distribution function to estimate the model distribution function F ,

and the sample mean to estimate the expectation µ corresponding to F.One

of the things we would like to know is how close a sample statistic is to the

model feature it is supposed to estimate. For instance, what is the probability

that the sample mean and µ diﬀer more than a given tolerance ε?Forthis

we need to know the distribution of

− µ. More generally, it is important

to know how a sample statistic is distributed in relation to the corresponding

model feature. For the distribution of the sample mean we saw a normal limit

approximation in Chapter 14. In this chapter we discuss a simulation proce-

dure that approximates the distribution of the sample mean for ﬁnite sample

size. Moreover, the method is more generally applicable to sample statistics

other than the sample mean.

18.1 The bootstrap principle

Consider the Old Faithful data introduced in Chapter 15, which we modeled

as the realization of a random sample of size n = 272 from some distribution

function F . The sample mean ¯x

of the observed durations equals 209.3. What

does this say about the expectation µ of F ? As we saw in Chapter 17, the value

209.3 is a natural estimate for µ, but to conclude that µ is equal to 209.3 is

unwise. The reason is that, if we would observe a new dataset of durations, we

will obtain a diﬀerent sample mean as an estimate for µ. This should not come

as a surprise. Since the dataset x

,...,x

is just one possible realization

of the random sample X

,...,X

, the observed sample mean is just one

possible realization of the random variable

270 18 The bootstrap

+ X

+ ···+ X

A new dataset is another realization of the random sample, and the cor-

responding sample mean is another realization of the random variable

Hence, to infer something about µ, one should take into account how realiza-

tions of

vary. This variation is described by the probability distribution

In principle

it is possible to determine the distribution function of

from

the distribution function F of the random sample X

,...,X

. However,

F is unknown. Nevertheless, in Chapter 17 we saw that the observed dataset

reﬂects most features of the “true” probability distribution. Hence the natural

thingtodoistocomputeanestimate

F for the distribution function F and

then to consider a random sample from

F and the corresponding sample mean

as substitutes for the random sample X

,...,X

from F and the random

variable

. A random sample from

F is called a bootstrap random sample,

or brieﬂy bootstrap sample, and is denoted by

∗

,...,X

∗

to distinguish it from the random sample X

,...,X

from the “true” F .

The corresponding average is called the bootstrapped sample mean,andthis

random variable is denoted by

∗

+ X

∗

+ ···+ X

∗

to distinguish it from the random variable

. The idea is now to use the

distribution of

∗

to approximate the distribution of

The preceding procedure is called the bootstrap principle for the sample mean.

Clearly, it can be applied to any sample statistic h(X

,...,X

) by approx-

imating its probability distribution by that of the corresponding bootstrapped

sample statistic h(X

∗

,...,X

∗

Bootstrap principle. Use the dataset x

,...,x

to com-

pute an estimate

F for the “true” distribution function F . Replace

the random sample X

,...,X

from F by a random sample

∗

,...,X

∗

from

F , and approximate the probability distribu-

tion of h(X

,...,X

)bythatofh(X

∗

,...,X

∗

Returning to the sample mean, the ﬁrst question that comes to mind is, of

course, how well does the distribution of

∗

approximate the distribution

In Section 11.1 we saw how the distribution of the sum of independent random

variables can be computed. Together with the change-of-units rule (see page 106),

the distribution of

can be determined. See also Section 13.1, where this is done

for independent Gam(2, 1) variables.

18.1 The bootstrap principle 271

? Or more generally, how well does the distribution of a bootstrapped

sample statistic h(X

∗

,...,X

∗

) approximate the distribution of the sam-

ple statistic of interest h(X

,...,X

)? Applied in such a straightforward

manner, the bootstrap approximation for the distribution of

by that of

∗

may not be so good (see Remark 18.1). The bootstrap approximation will

improve if we approximate the distribution of the centered sample mean:

− µ,

where µ is the expectation corresponding to F . The bootstrapped version

would be the random variable

∗

− µ

∗

where µ

∗

is the expectation corresponding to

F . Often the bootstrap approx-

imation of the distribution of a sample statistic will improve if we somehow

normalize the sample statistic by relating it to a corresponding feature of the

“true” distribution. An example is the centered sample median

Med(X

,...,X

) − F

inv

(0.5),

where we subtract the median F

inv

(0.5) of F . Another example is the nor-

malized sample variance

wherewedividebythevarianceσ

of F .

Quick exercise 18.1 Describe how the bootstrap principle should be applied

to approximate the distribution of Med(X

,...,X

) − F

inv

(0.5).

Remark 18.1 (The bootstrap for the sample mean). To see why

the bootstrap approximation for

may be bad, consider a dataset

,...,x

that is a realization of a random sample X

,...,X

from

an N (µ, 1) distribution. In that case the corresponding sample mean

has an N (µ, 1/n) distribution. We estimate µ by ¯x

and replace the ran-

dom sample from an N (µ, 1) distribution by a bootstrap random sample

∗

,...,X

∗

from an N (¯x

, 1) distribution. The corresponding boot-

strapped sample mean

∗

has an N (¯x

, 1/n) distribution. Therefore the

distribution functions G

and G

∗

of the random variables

and

∗

can

be determined:

(a)=Φ(

√

n(a − µ)) and G

∗

(a)=Φ(

√

n(a − ¯x

)).

In this case it turns out that the maximum distance between the two dis-

tribution functions is equal to

2Φ



√

n|¯x

− µ|



− 1.

272 18 The bootstrap

Since

has an N(µ, 1/n) distribution, this value is approximately equal to

2Φ (|z|/2)−1, where z is a realization of an N(0, 1) random variable Z.This

only equals zero for z = 0, so that the distance between the distribution

functions of

and

∗

will almost always be strictly positive, even for

large n.

The question that remains is what to take as an estimate

F for F .This

will depend on how well F can be speciﬁed. For the Old Faithful data we

cannot say anything about the type of distribution. However, for the software

data it seems reasonable to model the dataset as a realization of a random

sample from an Exp (λ) distribution and then we only have to estimate the

parameter λ. Diﬀerent assumptions about F give rise to diﬀerent bootstrap

procedures. We will discuss two of them in the next sections.

18.2 The empirical bootstrap

Suppose we consider our dataset x

,...,x

as a realization of a random

sample from a distribution function F . When we cannot make any assumptions

about the type of F , we can always estimate F by the empirical distribution

function of the dataset:

F (a)=F

(a)=

number of x

less than or equal to a

Since we estimate F by the empirical distribution function, the corresponding

bootstrap principle is called the empirical bootstrap. Applying this principle

to the centered sample mean, the random sample X

,...,X

from F is

replaced by a bootstrap random sample X

∗

,...,X

∗

from F

,andthe

distribution of

−µ is approximated by that of

∗

−µ

∗

,whereµ

∗

denotes

the expectation corresponding to F

. The question is, of course, how good

this approximation is. A mathematical theorem tells us that the empirical

bootstrap works for the centered sample mean, i.e., the distribution of

−µ

is well approximated by that of

∗

−µ

∗

(see Remark 18.2). On the other hand,

there are (normalized) sample statistics for which the empirical bootstrap fails,

such as

1 −

maximum of X

,...,X

based on a random sample X

,...,X

from a U(0,θ) distribution (see

Exercise 18.12).

Remark 18.2 (The empirical bootstrap for

−µ). For the centered

sample mean the bootstrap approximation works, even if we estimate F

by the empirical distribution function F

.IfG

denotes the distribution

function of

− µ and G

∗

the distribution function of its bootstrapped

version

∗

− µ

∗

, then the maximum distance between G

∗

and G

goes to

zero with probability one:

A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )

Подождите немного. Документ загружается.