A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику

Подождите немного. Документ загружается.

18.5 Exercises 283

a. Suppose we assume nothing about the distribution of the interfailure

times. Describe how one can obtain a bootstrap approximation for the

probability, i.e., describe the appropriate bootstrap simulation procedure

with one thousand repetitions and how the results of this simulation can

be used to approximate the probability.

b. Suppose we assume that F is the distribution function of an Exp(λ)dis-

tribution. Describe how one can obtain a bootstrap approximation for the

probability.

18.11 Consider the dataset of measured chest circumferences of 5732 Scottish

soldiers (see Exercises 15.1, 17.6, and 18.9). The Kolmogorov-Smirnov distance

between the empirical distribution function and the distribution function

¯x

of the normal distribution with estimated parameters ˆµ =¯x

=39.85

and ˆσ = s

=2.09 is equal to

=sup

a∈R

(a) − F

¯x

(a)| =0.0987,

where ¯x

and s

denote sample mean and sample standard deviation of the

dataset. Suppose we want to perform a bootstrap simulation with one thou-

sand repetitions for the KS distance to investigate to which degree the value

0.0987 agrees with the assumed normality of the dataset. Describe the appro-

priate bootstrap simulation that must be carried out.

18.12 To give an example where the empirical bootstrap fails, consider the

following situation. Suppose our dataset x

,...,x

is a realization of a

random sample X

,...,X

from a U (0,θ) distribution. Consider the nor-

malized sample statistic

=1−

where M

is the maximum of X

,...,X

.LetX

∗

,...,X

∗

be a boot-

strap random sample from the empirical distribution function of our dataset,

and let M

∗

be the corresponding bootstrap maximum. We are going to com-

pare the distribution functions of T

and its bootstrap counterpart

∗

=1−

∗

where m

is the maximum of x

,...,x

a. Check that P(T

≤ 0) = 0 and show that

P(T

∗

≤ 0) = 1 −



1 −



Hint: ﬁrst argue that P(T

∗

≤ 0) = P(M

∗

= m

), and then use the result

of Exercise 18.4.

284 18 The bootstrap

b. Let G

(t)=P(T

≤ t) be the distribution function of T

, and similarly let

∗

(t)=P(T

∗

≤ t) be the distribution function of the bootstrap statistic

∗

. Conclude from part a that the maximum distance between G

∗

and

can be bounded from below as follows:

sup

t∈R

∗

(t) − G

(t)|≥1 −



1 −



c. Use part b to argue that for all n, the maximum distance between G

∗

and G

is greater than 0.632:

sup

t∈R

∗

(t) − G

(t)|≥1 − e

−1

=0.632.

Hint: you may use that e

−x

≥ 1 − x for all x.

We conclude that even for very large sample sizes the maximum distance

between the distribution functions of T

and its bootstrap counterpart T

∗

is at least 0.632.

18.13 (Exercise 18.12 continued). In contrast to the empirical bootstrap, the

parametric bootstrap for T

does work. Suppose we estimate the parameter θ

of the U(0,θ) distribution by

θ =

n +1

, where m

= maximum of x

,...,x

Let now X

∗

,...,X

∗

be a bootstrap random sample from a U(0,

θ)dis-

tribution, and let M

∗

be the corresponding bootstrap maximum. Again, we

are going to compare the distribution function G

of T

=1−M

/θ with the

distribution function G

∗

of its bootstrap counterpart T

∗

=1−M

∗

θ.

a. Check that the distribution function F

of a U(0,θ) distribution is given

(a)=

for 0 ≤ a ≤ θ.

b. Check that the distribution function of T

(t)=P(T

≤ t)=1−(1 − t)

for 0 ≤ t ≤ 1.

Hint: rewrite P(T

≤ t)as1− P(M

≤ θ(1 − t)) and use the rule on

page 109 about the distribution function of the maximum.

c. Show that T

∗

has the same distribution function:

∗

(t)=P(T

∗

≤ t)=1−(1 − t)

for 0 ≤ t ≤ 1.

This means that, in contrast to the empirical bootstrap (see Exer-

cise 18.12), the parametric bootstrap works perfectly in this situation.

Unbiased estimators

In Chapter 17 we saw that a dataset can be modeled as a realization of a

random sample from a probability distribution and that quantities of interest

correspond to features of the model distribution. One of our tasks is to use the

dataset to estimate a quantity of interest. We shall mainly deal with the situ-

ation where it is modeled as one of the parameters of the model distribution

or as a certain function of the parameters. We will ﬁrst discuss what we mean

exactly by an estimator and then introduce the notion of unbiasedness as a

desirable property for estimators. We end the chapter by providing unbiased

estimators for the expectation and variance of a model distribution.

19.1 Estimators

Consider the arrivals of packages at a network server. One is interested in the

intensity at which packages arrive on a generic day and in the percentage of

minutes during which no packages arrive. If the arrivals occur completely at

random in time, the arrival process can be modeled by a Poisson process. This

would mean that the number of arrivals during one minute is modeled by a

random variable having a Poisson distribution with (unknown) parameter µ.

The intensity of the arrivals is then modeled by the parameter µ itself, and

the percentage of minutes during which no packages arrive is modeled by the

probability of zero arrivals: e

−µ

. Suppose one observes the arrival process for a

while and gathers a dataset x

,...,x

,wherex

represents the number of

arrivals in the ith minute. Our task will be to estimate, based on the dataset,

the parameter µ and a function of the parameter: e

−µ

This example is typical for the general situation in which our dataset is mod-

eled as a realization of a random sample X

,...,X

from a probability

distribution that is completely determined by one or more parameters. The

parameters that determine the model distribution are called the model param-

eters. We focus on the situation where the quantity of interest corresponds

286 19 Unbiased estimators

to a feature of the model distribution that can be described by the model

parameters themselves or by some function of the model parameters. This

distribution feature is referred to as the parameter of interest. In discussing

this general setup we shall denote the parameter of interest by the Greek

letter θ. So, for instance, in our network server example, µ is the model pa-

rameter. When we are interested in the arrival intensity, the role of θ is played

by the parameter µ itself, and when we are interested in the percentage of

idle minutes the role of θ is played by e

−µ

Whatever method we use to estimate the parameter of interest θ,theresult

depends only on our dataset.

Estimate. An estimate is a value t that only depends on the dataset

,...,x

, i.e., t is some function of the dataset only:

t = h(x

,...,x

This description of estimate is a bit formal. The idea is, of course, that the

value t, computed from our dataset x

,...,x

, gives some indication of

the “true” value of the parameter θ. We have already met several estimates in

Chapter 17; see, for instance, Table 17.2. This table illustrates that the value

of an estimate can be anything: a single number, a vector of numbers, even a

complete curve.

Let us return to our network server example in which our dataset x

,...,x

is modeled as a realization of a random sample from a Pois (µ) distribution.

The intensity at which packages arrive is then represented by the parameter µ.

Since the parameter µ is the expectation of the model distribution, the law

of large numbers suggests the sample mean ¯x

as a natural estimate for µ.

On the other hand, the parameter µ also represents the variance of the model

distribution, so that by a similar reasoning another natural estimate is the

sample variance s

The percentage of idle minutes is modeled by the probability of zero arrivals.

Similar to the reasoning in Section 13.4, a natural estimate is the relative

frequency of zeros in the dataset:

number of x

equal to zero

On the other hand, the probability of zero arrivals can be expressed as a

function of the model parameter: e

−µ

. Hence, if we estimate µ by ¯x

,we

could also estimate e

−µ

by e

−¯x

Quick exercise 19.1 Suppose we estimate the probability of zero arrivals

−µ

by the relative frequency of x

equal to zero. Deduce an estimate for µ

from this.

19.2 Investigating the behavior of an estimator 287

The preceding examples illustrate that one can often think of several estimates

for the parameter of interest. This raises questions like

Ĺ When is one estimate better than another?

Ĺ Does there exist a best possible estimate?

For instance, can we say which of the values ¯x

or s

computed from the

dataset is closer to the “true” parameter µ?Theanswerisno. The measure-

ments and the corresponding estimates are subject to randomness, so that

we cannot say anything with certainty about which of the two is closer to µ.

One of the things we can say for each of them is how likely it is that they are

within a given distance from µ. To this end, we consider the random variables

that correspond to the estimates. Because our dataset x

,...,x

is mod-

eled as a realization of a random sample X

,...,X

, the estimate t is a

realization of a random variable T .

Estimator. Let t = h(x

,...,x

) be an estimate based on the

dataset x

,...,x

.Thent is a realization of the random variable

T = h(X

,...,X

The random variable T is called an estimator.

The word estimator refers to the method or device for estimation. This is

distinguished from estimate, which refers to the actual value computed from

a dataset. Note that estimators are special cases of sample statistics. In the

remainder of this chapter we will discuss the notion of unbiasedness that

describes to some extent the behavior of estimators.

19.2 Investigating the behavior of an estimator

Let us continue with our network server example. Suppose we have observed

the network for 30 minutes and we have recorded the number of arrivals in

each minute. The dataset is modeled as a realization of a random sample

,...,X

of size n =30fromaPois(µ) distribution. Let us concentrate

on estimating the probability p

of zero arrivals, which is an unknown number

between 0 and 1. As motivated in the previous section, we have the following

possible estimators:

S =

number of X

equal to zero

and T =e

−

Our ﬁrst estimator S can only attain the values 0,

,...,1, so that in

general it cannot give the exact value of p

. Similarly for our second estima-

tor T , which can only attain the values 1, e

−1/30

, e

−2/30

,... . So clearly, we

288 19 Unbiased estimators

cannot expect our estimators always to give the exact value of p

on basis of

30 observations. Well, then what can we expect from a reasonable estimator?

To get an idea of the behavior of both estimators, we pretend we know µ

and we simulate the estimation process in the case of n =30observations.

Let us choose µ = ln 10, so that p

−µ

=0.1. We draw 30 values from

a Poisson distribution with parameter µ = ln 10 and compute the value of

estimators S and T . We repeat this 500 times, so that we have 500 values

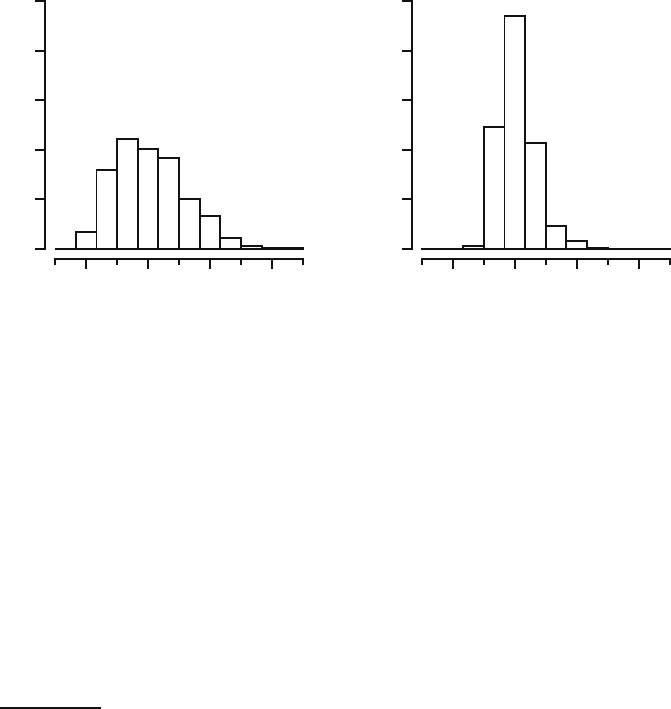
for each estimator. In Figure 19.1 a frequency histogram

of these values

for estimator S is displayed on the left and for estimator T on the right.

Clearly, the values of both estimators vary around the value 0.1, which they

are supposed to estimate.

0.0 0.1 0.2 0.3

100

150

200

250

0.0 0.1 0.2 0.3

100

150

200

250

Fig. 19.1. Frequency histograms of 500 values for estimators S (left) and T (right)

of p

=0.1.

19.3 The sampling distribution and unbiasedness

We have just seen that the values generated for estimator S ﬂuctuate around

=0.1. Although the value of this estimator is not always equal to 0.1, it

is desirable that on average, S is on target, i.e., E [S]=0.1. Moreover, it is

desirable that this property holds no matter what the actual value of p

is,

i.e.,

E[S]=p

irrespective of the value 0 <p

< 1. In order to ﬁnd out whether this is

true, we need the probability distribution of the estimator S.Ofcoursethis

In a frequency histogram the height of each vertical bar equals the frequency of

values in the corresponding bin.

19.3 The sampling distribution and unbiasedness 289

is simply the distribution of a random variable, but because estimators are

constructed from a random sample X

,...,X

, we speak of the sampling

distribution.

The sampling distribution. Let T = h(X

,...,X

)bean

estimator based on a random sample X

,...,X

. The probabil-

ity distribution of T is called the sampling distribution of T .

The sampling distribution of S can be found as follows. Write

S =

where Y is the number of X

equal to zero. If for each i we label X

=0as

a success, then Y is equal to the number of successes in n independent trials

with p

as the probability of success. Similar to Section 4.3, it follows that Y

has a Bin(n, p

) distribution. Hence the sampling distribution of S is that of

a Bin (n, p

) distributed random variable divided by n. This means that S is

a discrete random variable that attains the values k/n,wherek =0, 1,...,n,

with probabilities given by







S =



=P(Y = k)=





(1 − p

)

n−k

The probability mass function of S for the case n =30andp

=0.1is

displayed in Figure 19.2. Since S = Y/n and Y has a Bin(n, p

) distribution,

it follows that

E[S]=

E[Y ]

= p

So, indeed, the estimator S for p

has the property E[S]=p

. This property

reﬂects the fact that estimator S has no systematic tendency to produce

0.0 0.2 0.4 0.6 0.8 1.0

0.00

0.05

0.10

0.15

0.20

0.25

(a)

····················

Fig. 19.2. Probability mass function of S.

290 19 Unbiased estimators

estimates that are larger than p

, and no systematic tendency to produce

estimates that are smaller than p

. This is a desirable property for estimators,

and estimators that have this property are called unbiased.

Definition. An estimator T is called an unbiased estimator for the

parameter θ,if

E[T ]=θ

irrespective of the value of θ. The diﬀerence E [T ] − θ is called the

bias of T ; if this diﬀerence is nonzero, then T is called biased.

Let us return to our second estimator for the probability of zero arrivals in

the network server example: T =e

−

. The sampling distribution can be

obtained as follows. Write

T =e

−Z/n

where Z = X

+ X

+ ···+ X

. From Exercise 12.9 we know that the random

variable Z, being the sum of n independent Pois (µ) random variables, has

a Pois (nµ) distribution. This means that T is a discrete random variable

attaining values e

−k/n

,wherek =0, 1,... and the probability mass function

of T is given by



−k/n





T =e

−k/n



=P(Z = k)=

−nµ

(nµ)

The probability mass function of T for the case n =30andp

=0.1is

displayed in Figure 19.3. From the histogram in Figure 19.1 as well as from

the probability mass function in Figure 19.3, you may get the impression

that T is also an unbiased estimator. However, this not the case, which follows

immediately from an application of Jensen’s inequality:

0.0 0.2 0.4 0.6 0.8 1.0

0.00

0.01

0.02

0.03

0.04

0.05

(a)

·····································

····

·····

············································

Fig. 19.3. Probability mass function of T .

19.3 The sampling distribution and unbiasedness 291

E[T ]=E



−



> e

−E

[

]

where we have a strict inequality because the function g(x)=e

−x

is strictly

convex (g



(x)=e

−x

> 0). Recall that the parameter µ equals the expectation

of the Pois(µ) model distribution, so that according to Section 13.1 we have





= µ. We ﬁnd that

E[T ] > e

−µ

= p

which means that the estimator T for p

has positive bias. In fact we can

compute E [T ] exactly (see Exercise 19.9):

E[T ]=E



−



−nµ(1−e

−1/n

)

Note that n(1 − e

−1/n

) → 1, so that

E[T ]=e

−nµ(1−e

−1/n

)

→ e

−µ

= p

as n goes to inﬁnity. Hence, although T has positive bias, the bias decreases

to zero as the sample size becomes larger. In Figure 19.4 the expectation of

T is displayed as a function of the sample size n for the case µ = ln(10). For

n = 30 the diﬀerence between E[T ]andp

=0.1 equals 0.0038.

0 5 10 15 20 25 30

0.00

0.05

0.10

0.15

0.20

0.25

E[T ]

··

.....................................................................................................

Fig. 19.4. E[T ] as a function of n.

Quick exercise 19.2 If we estimate p

−µ

by the relative frequency of

zeros S = Y/n, then we could estimate µ by U = −ln(S). Argue that U is a

biased estimator for µ. Is the bias positive or negative?

We conclude this section by returning to the estimation of the parameter µ.

Apart from the (biased) estimator in Quick exercise 19.2 we also considered

292 19 Unbiased estimators

thesamplemean

and sample variance S

as possible estimators for µ.

These are both unbiased estimators for the parameter µ.Thisisadirect

consequence of a more general property of

and S

, which is discussed in

the next section.

19.4 Unbiased estimators for expectation and variance

Sometimes the quantity of interest can be described by the expectation or

variance of the model distribution, and is it irrelevant whether this distribution

is of a parametric type. In this section we propose unbiased estimators for

these distribution features.

Unbiased estimators for expectation and variance. Sup-

pose X

,...,X

is a random sample from a distribution with

ﬁnite expectation µ and ﬁnite variance σ

.Then

+ X

+ ···+ X

is an unbiased estimator for µ and

n − 1



i=1

−

)

is an unbiased estimator for σ

The ﬁrst statement says that E





= µ, which was shown in Section 13.1.

The second statement says E





= σ

. To see this, use linearity of expecta-

tions to write





n − 1



i=1



−

)



Since E





= µ,wehaveE



−



=E[X

]−E





= 0. Now note that

for any random variable Y with E [Y ]=0,wehave

Var(Y )=E





− (E [Y ])





Applying this to Y = X

−

, it follows that



−

)



=Var



−



Note that we can write

−

n − 1

−



j=i

A Modern Introduction to Probability and Statistics, Understanding Why and How - Dekking, Kraaikamp, Lopuhaa, Meester (Современное введение в теорию вероятностей и статистику - Как? и Почему? )

Подождите немного. Документ загружается.