Золотаревский В.С. Механические свойства металлов
Подождите немного. Документ загружается.


а
2
J
•
о
"1
'1
О
=ft-
rf
Рис.
89.
Схемы
дифференциального
конденсаторного
датчика
(а)
и
индуктивного
тензометра
(6)
которой
из-за
перемещения
сердечников
возникает
разность
на"'"
пряжений,
пропорциональная
удлинению
и
фиксируемая
после
усиления
самопишущим
прибором.
Возможна
непрерывная
за
пись
изменения
расчетной
длины
образца
в
зависимости
от
на
грузки.
Методика
определения
предела
пропорциональности
с
помо
щью
тензометров
сводится
к
следующему.
Сначала
образец
без
тензометров
растягивают
до
достижения
начального
усилия
Р
О
'
соответствуюшего
-10
%
от
примерно
ожидаемого
предела
про
порциональности.
Затем
на
образец
устанавливают
тензометр,
обеспечивающий
измерение
удлинений
с
двух
противоположных
сторон
образца.
Последующее
нагружение
образца
про
изводят
ступенями
и
сразу
же
после
каждой
ступени
нагружения
(без
раз
грузки)
снимают
показания
тензометров.
До
напряжения,
отве
чающего
70-80
%
ожидаемого
а
пц
,
дают
три
-
пять
крупных
(и
равных
по
величине)
ступеней
I1Р.
Дальнейшие
ступени
I1Р'
де
лают
более
мелкими:
I1а:::;
20
МПа.
Испытание
прекращают,
когда
прирост
удлинения
М
=
11
~p
+ f
увеличится
в
1,5-3
раза
по
срав
нению
со
средним
приростом
деформации
11'
(при
той
же
степе-
ер
ни
нагружения)
на
прямолинейном
участке
кривой
растяжения.
Искомая
нагрузка
Р
ПЦ
должна
отвечать
приросту
удлинения
М
=
11'
+/, ,
где
/,
-
заданный
допуск
на
отклонение
от
закона
ер
зад зад
пропорциональности.
Обычно!,ад
=
0,511'.
Если
после
очередной
малой
ступени
нагружения
на
I1Р!
мы
получим
М
>
11
' +
!'ад'
то
для
определения
Р
ПЦ
допускается
линейная
интерполяция.
Например,
11
'
равно
восьми
делениям
шкалы
тензометра,
а
1"
-
четырем
~
~
делениям.
При
нагрузке
40000
Н
величина
I1(
равна
десяти
деле-
ниям
(не
хватает
двух
делений
для
получения
!,ад).
После
очеред-
170

ной
ступени
нагружения
(I'!.Р'=
1000
Н)
величина
M
i
+
1
составляет
14
делений.
Следовательно,
приросту
усилия
на
1000
Н
соответ
ствуют
четыре
деления
шкалы
тензометра,
на
одно
деление
при
ходится
250
Н.
Тогда
Р
= 40000 +
2250
= 40500
Н.
nu
При
определении
предела
пропорциональности
можно
оце-
нить
и
величину модуля
нормальной
упругости.
Для
этого
необхо
димо
перевести
использованную
ступень
нагружения
I'!.Р
(или
I'!.Р)
в
соответствующий
прирост
напряжений
I'!.О",
а
среднее
абсолют
ное
удлинение
I'!.
в
упругой
области,
отвечающее
каждой
ступе-
ер
ни,
-
В
относительное
I'!.8.
Поскольку
в
области
упругой
деформа-
ции
поперечное
селение
образца
почти
не
меняется,
I'!.О"
~
I'!.S,
а
I'!.8
очень
близко
к
приросту
истинного
относительного
удлине
ния
I'!.е.
Тогда
Е
=
I'!.S/
I'!.e
~
I'!.О"/
I'!.8.
При
испытаниях
на
растяжение
может
быть
определен
коэф
фициент
Пуассона.
Для
этого
на
образец
в
виде
широкой
пласти
ны
устанавливают
два
тензометра
для
измерения
поперечной
и
продольной
деформации.
П
р
е
Д
е
л
у
пру
г
о
с
т
и.
Следующая
характерная
точка
на
первичной
диаграмме
растяжения
(см.
рис.
86) -
точка
е.
Ей
отве
чает
нагрузка,
по
которой
рассчитывают
условный
предел
упруго
сти
-
напряжение,
при
котором
остаточное
удлинение
достигает
заданной
величины,
обычно
0,05
%,
иногда
меньше
-
вплоть
до
0,005
%.
Использованный
при
расчете
допуск
указывается
в
обо
значении
условного
предела
упругости:
0"0,05'
0"0,01
И
Т.
д.
Предел
упругости
характеризует
напряжение,
при
котором
появляются
первые
признаки
макропластической
деформации.
В
связи
с
малым
допуском
по
остаточному
удлинению
даже
0"0,05
трудно
с
достаточной
точностью
определить
по
первичной
диаг
рамме
растяжения.
Поэтому
в
тех
случаях,
когда
высокой
точно
сти
не
требуется,
предел
упругости
принимается
равным
пределу
пропорциональности.
Если
же
необходима
точная
количествен
ная
оценка
0"0,05'
то
используют
тензометры.
Методика
определе
ния
0"0,05
во
многом
аналогична
описанной
для
О"пu'
но
имеется
одно
принципиальное
различие.
Поскольку
при
определении
пре
дела
упругости
допуск
задается
по
веЛИ'lине
остаточной
дефор
мации,
после
каждой
ступени
нагружения
необходимо
разгру
жать
образец
до
начального
напряжения
0"0
~
10%
от
ожидаемого
171

0"005
И
затем
только
измерять
удлинение
по
тензометру.
,
Если
масштаб
записи
диаграммы
растяжения
по
оси
удлине
ний
составляет
50:1
и
более,
а
по
оси
нагрузок
::;10
МПа
на
1
мм,
допускается
графическое
определение
0"0,05'
Для
этого
по
оси
уд
линений
от
начала
координат
откладывают
отрезок
ОК
= 0,05
10/
100
и через
точку
К
проводят
прямую,
параллельную
прямоли
нейному
участку
диаграммы
(рис.
90).
Ордината
точки
е
будет
со
ответствовать
величине
нагрузки
Ро,05'
определяющей
условный
предел
упругости:
0"0,05 =
Ро,05
/ F
o
П
р
е
Д
е
л
т
е
к
у
ч
е с
т
и.
При
отсутствии
на
диаграмме
растяжения
зуба
и
площадки
текучести
рассчитывают
условный
предел
текучести
-
напряжение,
при
котором
остаточное
удлине
ние
достигает
заданной
величины,
обычно
0,2
%.
Соответственно
условный
предел
текучести
обозначается
0"0,2'
Как
видно,
эта
ха
рактеристика
отличается
от
условного
предела
упругости
только
величиной
допуска.
Предел
текучести
характеризует
напряжение,
при
котором
происходит
более
полный
переход к
пластической
деформации.
Наиболее
точная
оценка
величины
0"0,2
может
быть
выполнена
при
использовании
тензометров.
Методика
здесь
полностью
ана
логична
при
меняемой
для
определения
0"0,05'
Поскольку
допуск
по
удлинению
для
расчета
условного
предела
текучести
относитель
но
велик,
его
часто
определяют
графически
по
диаграмме
растя
жения,
если
последняя
записана
в
достаточно
большом
масшта
бе
(не
менее
1
О:
1
по
оси
деформаций).
Делается
это
так
же,
как
при
расчете
предела
упругости
(см.
рис.
90),
только
отрезок
ОК=
р
l'
~ll----::#.($~J
OH~-----
.1l
~
0,05
или
0,2%
от
/"
Рис.
90.
Определение
УСЛОВ-
ных
предела
упругости
и
те-
КУ'lести
ПО
диаграмме
рас-
тяжения
172
0,2
10/100
Условные
пределы
пропорциональности,
упругости
и
текучести
характеризуют
сопро
тивление
материала
малым
деформациям.
Величина
их
н("значительно
отличается
от
истинных
напряжений,
отвечающих
соот
ветствующим
допускам
по
деформации.
Тех
ническое
значение
этих
пределов
сводится
к
тому,
чтобы
оценить
уровни
напряжений,
под
действием
которых
та
или
иная
деталь
может
работать,
не
подвергаясь
остаточной
деформации
(предел
пропорциональности)
или
деформируясь
на
какую-то
небольшую
допускаемую
величину,
определяемую
ус-

ловиями
эксплуатации
(ао,оl'
СУ
о
,О5'
СУ
О
,2
И
т.
д.).
Учитывая,
что
в
современной
технике
возможность
остаточного
изменения
раз
меров
деталей
и
конструкций
лимитируrпся
все
более
жестко,
становится
ясной
насущная
необходимость
точного
знания
пре
делов
пропорциональности,
упругости
и
текучести,
которые
ши
роко
используются
в
конструкторских
расчетах.
Физический
смысл
предела
пропорциональности
любого
ма
териала
настолько
очевиден,
что
не
требует
специального
обсуж
дения.
Действительно,
CJ
пц
для
моно-
И поликристалла,
гомоген
ного металла
и
гетерофазного
сплава
-
это
всегда
максимальное
напряжение,
до
которого
при
растяжении
соблюдается
закон
Гука
и
макропластическая
деформация
не
наблюдается.
Следует
по
мнить,
что
до
достижения
CJ
пц
в
отдельных
зернах
поликристалли
ческого
образца (при
их
благоприятной
ориентировке,
наличии
концентраторов
напряжений)
может
начаться
пластическая
де
формация,
которая,
однако,
не
приведет
к
заметному
удлине
нию
всего
образца,
пока
деформацией
не
окажется
охваченным
большинство
зерен.
Начальным
стадиям
макроудлинения
образца
соответствует
предел
упругости.
Для
благоприятно
ориентирован
ного
монокристалла
он
должен
быть
близок
к
критическому
ска
лывающему
напряжению,
конечно,
после
перевода
касательного
напряжения
в
эквивалентное
ему
нормальное
по
формуле
(24).
Естественно,
при
разных
кристаллографических
ориентировках
монокристалла
предел
упругости
будет
различен.
У
достаточно
мелкозернистого
поликристалла
в
отсутствие
текстуры
предел
упругости
изотропен,
одинаков
во
всех
направлениях.
Природа
условного
предела
текучести
поликристалла
в
прин
ципе
аналогична
природе
предела
упругости.
Но
именно
предел
текучести
является
наиболее
распространенной
и
важной
харак
теристикой
сопротивления
металлов
и
сплавов
малой
пластичес
кой
деформации.
Поэтому
физический
смысл
предела
текучести
и
его
зависимость
от
различных
факторов
необходимо
проанали
зировать
подробнее.
Плавный
переход
от
упругой
к
пластической
деформации
(без
зуба
и
площадки
текучести)
наблюдается
при
растяжении
таких
металлов
и
сплавов,
в
которых
имеется
достаточно
большое
ко
личество
подвижных,
незакрепленных
дислокаций
в
исходном
состоянии
(до
начала
испытания),
Напряжение,
необходимое
для
начала
пластической
деформации
поликристаллов
этих
материа
лов,
оцениваемое
через
условный
предел
текучести,
определяет-
173

ся
силами
сопротивления
движению
дислокаций
внугри
зерен,
легкостью
передачи
деформации
через
их
границы
и
размером
зерен.
Эти
же
факторы
определяют
и
величину
физического
предела
текучести
а
т
-
напряжения,
при
котором
образец
деформируется
под
действием
практически
неизменной
растягивающей
нагрузки
Р
Т
(см.
рис.
86,
площадка
текучести
на
пунктирной
кривой).
Физи
ческий
предел
текучести
часто
называют
нижним
в
отличие
от
BepxHero
l
предела
текучести,
рассчитываемого
·по
нагрузке,
со
ответствующей
вершине
зуба
текучести
и
(см.
рис.
86):
а
=Р
IF.
Т.В Т.В
О
(53)
Образование
зуба
и
площадки
текучести
(так
называемое
яв
ление
резкой
текучести)
внешне
выглядит
следующим
образом.
Упругое
растяжение
приводит
к
плавному
подъему
сопротивле
ния
деформированию
вплоть
до
а
т
••
затем
происходит
относи
тельно
резкий
спад
напряжений
до
а
т
.•
и
последующая
деформа
ция
(обычно
на
0,1-1%)
идет
при
неизменном
внешнем
усилии
-
образуется
площадка
текучести.
Во
время
удлинения,
соответ
ствующего
этой
площадке,
образец
на
рабочей
длине
покрывает
ся
характерными
полосами
Чернова
-
Людерса,
в
которых
лока
лизуется
деформация.
Поэтому
величину
удлинения
на
площадке
текучести
(0,1-1
%)
часто
называют
деформацией
Чернова
-
Людерса.
Явление
резкой
текучести
наблюдается
у
многих
технически
важных
металлических
материалов
и
поэтому
имеет
большое
прак
тическое
значение.
Оно
представляет
также
общий
теоретический
интерес
с
точки
зрения
понимания
природы
начальных
стадий
пластической
деформации.
В
последние
десятилетия
показано,
что
зуб
и
площадку
теку
чести
можно
получить
при
растяжении
моно-
и
поликристаллов
металлов
и
сплавов
с
различными
решетками
и
микроструктурой.
Наиболее
часто
фиксируется
резкая
текучесть
при
испытании
ме
таллов
с
о.
ц.
к.
решеткой
и сплавов
на
их
основе.
Естественно,
практическое
значение
резкой
текучести
для
этих
металлов
осо-
I
В
общем
случае
нижний
предел
текучести
О'т.1I
-
это
наименьшая
величина
напряжения
течения
без
учета
зуба
текучести,
если
он
наблюдается,
а
верхний
-
О'т
.•
-
напряжение,
соответствующее
первому
пику
нагрузки,
зарегистрированному
при
течении
образца.
174

бенно
велико,
и
большинство
теорий
также
разрабатывалось
при
менительно
к
особенностям
этих
l-1fатериалов.
Использование
дис
локационных
представлений
для
объяснения
резкой
текучести
было одним
из
первых
и
очень
плодотворных
приложений
теории
дислокаций.
Вначале
образование
зуба
и
площадки
текучести
в
о.
ц.
к.
ме
таллах
связывали
с
эффективной
блокировкой
дислокаций
при
месями.
Известно,
что
в
о.
ц.
к.
решетке
атомы
примесей
внедре
ния
образуют
не
обладающие
шаровой
симметрией
поля
упругих
напряжений
и
взаимодействуют
с
дислокациями
всех
типов,
в
том
числе
с
чисто
винтовыми.
Уже
при
малых
концентрациях
[<10-1-10-2 %
(ат.)]
примеси
(например,
азот
и
углерод
в
желе
зе)
способны
блокировать
все
дислокации,
имеющиеся
в
метал
ле
до
деформации.
Тогда,
по
Коттреллу,
для
начала
движения
дислокаций
и
для
начала
пластического
течения
необходимо
при
ложить
напряжение,
гораздо
большее,
чем
это
требуется
для
перемещения
дислокаций,
свободных
от
примесных
атмосфер.
Сле
довательно,
вплоть
до
момента
достижения
верхнего
предела
те
кучести
заблокированные
дислокации
не
могут
начать
двигаться,
и
деформация
идет
упруго.
После
достижения
а
т
•
по
крайней
мере
часть
этих
дислокаций
(расположенных
в
плоскостях
действия
максимальных
касательных
напряжений)
отрывается
от
своих
атмосфер
и
начинает
перемещаться,
производя
пластическую
деформацию.
Последующий
спад
напряжений
-
образование
зуба
текучести
-
происходит
потому,
что
свободные
от
примесных
атмосфер
и
более
подвижные
дислокации
могут
скользить
неко
торое
время
под
действием
меньших
напряжений
а
тн
пока
их
тор
можение
не
вызовет
начала
обычного
деформационного
упроч
нения.
Подтверждением
правильности
теории
Коттрелла
служат
ре
зультаты
следующих
простых
опытов.
Если
продеформировать
железный
образец,
например
до
точки
А
(рис.
91),
разгрузить
его
и
тут
же
вновь
растянуть,
то
зуба
и
площадки
текучести
не
воз
никнет,
потому
что
после
предварительного
растяжения
в
новом
исходном
состоянии
образец
содержал
множество
подвижных,
свободных
от
примесных
атмосфер
дислокаций.
Если
теперь
пос
ле
разгрузки
от
точки
А
образец
выдержать
при
комнатной
или
слегка
повышенной
температуре,
т.
е.
дать
время
для
конденсации
примесей
на
дислокациях,
то
при
новом
растяжении
на
диаграм
ме
опять
появится
зуб
и
площадка
текучести.
175
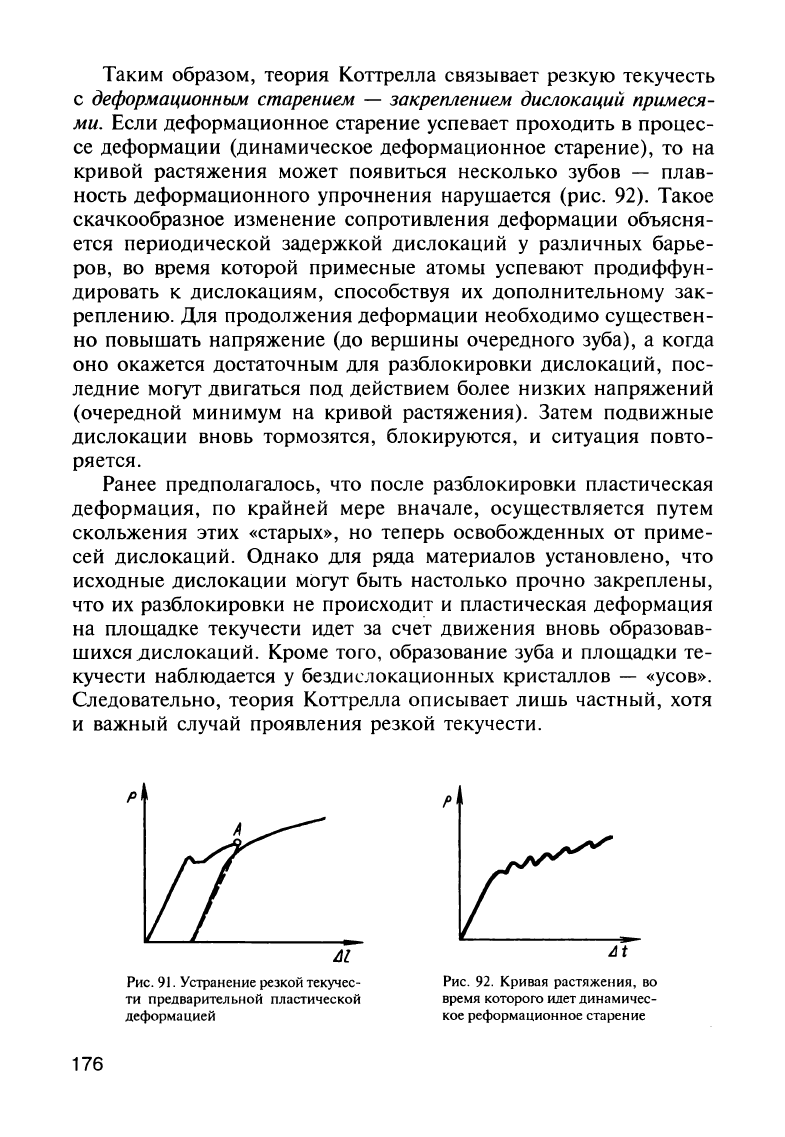
Таким
образом,
теория
Коттрелла
связывает
резкую
текучесть
с
деформационным
старением
-
закреплением
дислокаций
nрuмеся
ми.
Если
деформационное
старение
успевает
проходить
в
процес
се
деформации
(динамическое
деформационное
старение),
то
на
кривой
растяжения
может
появиться
несколько
зубов
-
плав
ность
деформационного
упрочнения
нарушается
(рис.
92).
Такое
скачкообразное
изменение
сопротивления
деформации
объясня
ется
периодической
задержкой
дислокаций
у
различных
барье
ров,
во
время
которой
примесные
атомы
успевают
продиффун
дировать
к
дислокациям,
способствуя
их
дополнительному
зак
реплению.
Для
продолжения
деформации
необходимо
существен
но
повышать
напряжение
(до
вершины
очередного
зуба),
а
когда
оно
окажется
достаточным
для
разблокировки
дислокаций,
пос
ледние
могут
двигаться
под
действием
более
низких
напряжений
(очередной
минимум
на
кривой
растяжения).
Затем
подвижные
дислокации
вновь
тормозятся,
блокируются,
и
ситуация
повто
ряется.
Ранее
предполагалось, что
после
разблокировки
пластическая
деформация,
по
крайней
мере
вначале,
осуществляется
путем
скольжения
этих
«старых»,
но
теперь
освобожденных
от
приме
сей
дислокаций.
Однако
для
ряда
материалов
установлено,
что
исходные
дислокации
могут
быть
настолько
прочно
закреплены,
что
их
разблокировки
не
происходит
и
пластическая
деформация
на
площадке
текучести
идет
за
счет
движения
вновь
образовав
шихся
дислокаций.
Кроме
того,
образование
зуба
и
площадки
те
кучести
наблюдается
у
бездислокационных
кристаллов
-
«усов».
Следовательно,
теория
Коттрелла
описывает
лишь
частный,
хотя
и
важный
случай
проявления
резкой
текучести.
176
р
Рис.
91.
Устранение
резкой
текучес
ти
предварительной
пластической
деформацией
р
Рис.
92.
Кривая
растяжения,
во
время
которого
идет
динамичес
кое
реформационное
старение
Основой
современной
общей
теории
резкой
текучести,
кото
рую
еще
нельзя
считать
окончательно
установившейся,
является
все
то
же
положение,
ВЬЩВИНУ'гое
Коттреллом:
зуб
и
площадка
текучести
обусловлены
резким
увеличением
числа
подвижных
дислокаций
в
начале
пластического
течения.
Это
значит,
что
для
их
появления
требуется
выполнение
двух
условий:
1)
в
исходном
образце
число
свободных
дислокаций
должно
быть
очень
малым,
и
2)
оно
должно
иметь
возможность
быстро
увеличиться
по
тому
или
иному
механизму
в
самом
начале
пластической
деформации.
Недостаток
подвижных
дислокаций
в
исходном
образце
мо
жет
быть
связан
либо
с
высоким
совершенством
его
субструкту
ры
(например,
в
усах)
либо
с
закреплением
большинства
имею
щихся
дислокаций.
По
Коттреллу,
такое
закрепление
может
быть
достигнуто
образованием
примесных
атмосфер.
Возможны
и
дру
гие
способы
закрепления,
например
частицами
второй
фазы.
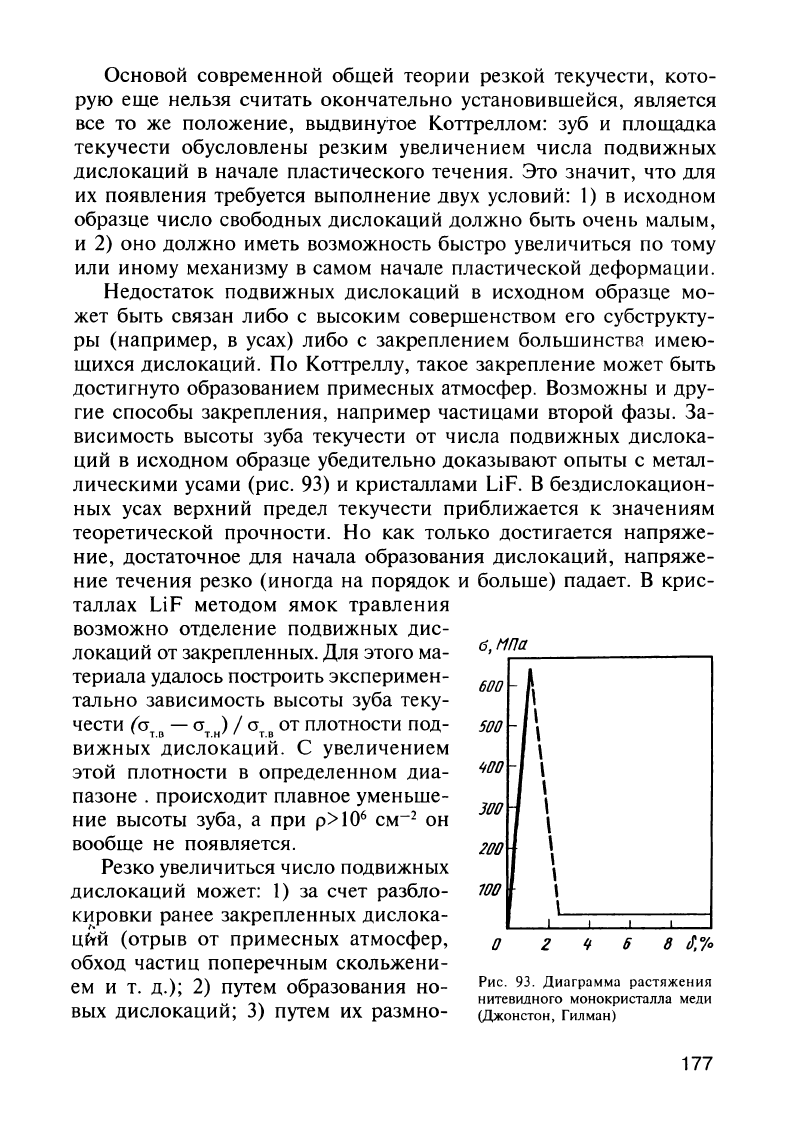
За
висимость
высоты
зуба
текучести
от
числа
подвижных
дислока
ций
в
исходном
образце
убедительно
доказывают
опыты
с
метал
лическими
усами
(рис.
93)
и
кристаллами
LiF.
В
бездислокацион
ных
усах
верхний
предел
текучести
приближается
к
значениям
теоретической
прочности.
Но
как
только
достигается
напряже
ние,
достаточное
для
начала
образования
дислокаций,
напряже
ние
течения
резко
(иногда
на
порядок
и
больше)
падает.
В
крис
таллах
LiF
методом
ямок
травления
возможно
отделение
подвижных
дис
локаций
от
закрепленных.
для
этого
ма
териала
удалось
построить
эксперимен
тально
зависимость
высоты
зуба
теку
чести
(а
т
.• -
а
т
) /
а
т
.•
от
плотности
под
вижных
дислокаций.
С
увеличением
этой
плотности
в
определенном
диа
пазоне
.
происходит
плавное
уменьше
ние
высоты
зуба,
а
при
р>
106
см-
2
он
вообще
не
появляется.
Резко
увеличиться
число
подвижных
дислокаций
может:
1)
за
счет
разбло
к~ровки
ранее
закрепленных
дислока
цhй
(отрыв
от
примесных
атмосфер,
обход
частиц
поперечным
скольжени
ем
и
т.
д.);
2)
путем
образования
но
вых
дислокаций;
3)
путем
их
размно-
б,I1.r-'ПО
_______
---,
БОО
1-
~
500 '
,
'100
JOO
20В
100
,
,
,
,
\
\
,
,
\
L
О
2 * 5 8
tf.'Yo
Рис.
93.
Диаграмма
растяжения
нитевидного
монокристалла
меди
(Джонстон,
Гилман)
177

жения
в
результате
взаимодействия.
Последние
два
способа
уве
личения
плотности
подвижных
дислокаций
могут
реализоваться
по
всем
известным
механизмам:
генерированием
источниками
Франка-Рида,
границами
зерен,
частицами
второй
фазы,
раз
множением
путем
двойного
поперечного
скольжения,
рекомби
нацией
и
т.
д.
В
общем
виде
возможность
возникновения
резкой
текучести
в
материале
с
малой
исходной
плотностью
подвижных
дислокаций
и
быстрым
ее
увеличением
в
начале
пластического
течения
опи
сывается
теорией
Гана.
Предположим,
что
наш
образец
растяги
вается
с
постоянной
скоростью
деформации.
Его
удлинение
е
со
стоит
из
упругой
е
у
и
пластической
е
п
составляющих.
Скорость
упругой
составляющей
удлинения
е
у
=
SjE,
где
S -
скорость
изменения
напряжения;
Е
-
модуль
упругости.
Скорость
пластической
составляющей
удлинения
е
п
=
bLv,
где
L -
общая
длина
подвижных
дислокаций
в
единице
объема,
v -
средняя
скорость
их
движения.
Величина
v
сильно
зависит
от
действующего
напряжения:
v =
KS",
причем
постоянная
n
для
металлов
имеет
порядок
101-102
(К
-
коэффициент).
С
учетом
деформационного
упрочнения
v = K(S - qe)",
где
q =
dS/dе
п
-
коэффициент
деформационного
упрочнения,
а
qе
п
характеризует
величину
напряжений,
действующих
на
сколь
зящую
дислокацию
в
результате
упругого
взаимодействия
с
дру
гими
дислокациями.
По
экспериментальным
данным,
L=K'e~+
L
o
•
где
К'
и
а
-
постоянные;
L
o
-
длина
подвижных
дислокаций
в
объеме
образца
до
начала растяжения.
В
результате
скорость
деформации
178
е
=
е
у
+
е
п
=
S/E+
bK(K'e~
+ L
o
}
(S-
qe)".
При
упругой
деформации
SJ::::Ee
y
,
а
при
пластической
SJ::::qe+
[e/Kb(L
o
+
K'e~}]I/II.
(54)
(55)
На
рис.
94
показаны
кривые,
соответствующие
уравнениям
(54)
и
(55),
а
также
суммарная
диаграмма
растяжения.
Зуб
текучести
образуется
на
ней
из-за
первоначального
сни
жения
S
в
соответствии
с
формулой
(55),
если
минимум
этой
кривой
лежит
правее
прямой
S=Ee
y
(см.
рис.
94),
Чем
меньше
n
и
длина
(плотность)
подвижных
дислокаций
L
o
в
исходном
состоя
нии,
тем
выше
будет
зуб
текучести.
При
типичных
для
железа
значениях
величин,
входящих
в
уравнения
(54)
и
(55),
резкая
текучесть
должна
быть
заметна
при
L
o
<103
см-
2
(n=35),
т.
е.
при
очень
низкой
плотности
подвижных
дислокаций.
До
сих
пор,
анализируя
природу
резкой
текучести,
мы
рас
сматривали
только
дислокационные
процессы
внутри
кристал
лов,
не
учитывая
влияния
границ
зерен
в
поликристаллах
и
та
кую
важную
особенность
деформации
на
площадке
текучести,
как
распространение
полос
Чернова-Людерса.
Эти
полосы
по
являются
в
результате
выхода
на
поверхность
образца
областей,
е
Рис.
94.
Кривые
напряжение
-
деформация,
соответствующие
уравнениям
(54)
и
(55)
Рис.
95.
Пластическая
деформация
в
полосе
Чернова
-
Людерса
(по
Мак
Лину)
179
