Зінченко О.П., Степанюк Я.В. Біометрія. Частина ІІ. Основи варіаційної статистики

Подождите немного. Документ загружается.

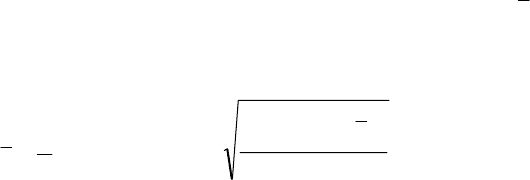
Оцінка істотності належності експериментального розподілу

частот у класах до теоретично відомого стандарту.

В біології є багато випадків, коли експериментатор має підстави

очікувати в досліді певного відомого теоретичного розподілу даних.

Наприклад, при моногібридному схрещуванні у другому поколінні генетик

має підстави очікувати розщеплення ознак, згідно з законом Менделя, у

пропорції 3 : 1, а при дигібридному

схрещуванні – в пропорції 9 : 3 : 3 : 1.

Зрозуміло, що ідеального співвідношення ознак або явищ у реальному

експерименті ми не дістаємо. Отже, постає питання, чи можна прийняти дану

теоретичну пропорцію як типову характеристику нашого експерименту, чи,

може, слід запропонувати іншу. Типовим статистичним апаратом такого

дослідження є обчислення критерію оцінки гіпотез хі-квадрат.

Оцінка істотності гіпотези

про нормальний тип розподілу варіант в

експериментальній вибірці.

Задачі цього типу принципово важливі в біометрії, оскільки на

практиці часто виходять з апріорного припущення, що добуті

експериментальні дані відповідають нормальному закону. Насправді таке

твердження потребує доведення, причому з достатньою імовірністю, не

меншою за 0,95.

Першим етапом доведення нормальної гіпотези (після групування

експериментальних даних

на класи) є розрахунок теоретично передбачених

частот у класах для ідеального випадку нормального розподілу – так звана

нормальна апроксимація експериментальних даних. Для проведення

нормальної апроксимації даних треба, щоб обсяг експериментальної вибірки

був великий (

n >

).Середнє арифметичне

і середнє квадратичне

відхилення

обчислюємо за формулами:

i ц

=⋅

∑

(

)

fx x

x ц

−

∑

де

частота в класах (фактично отримані в експерименті частоти ми

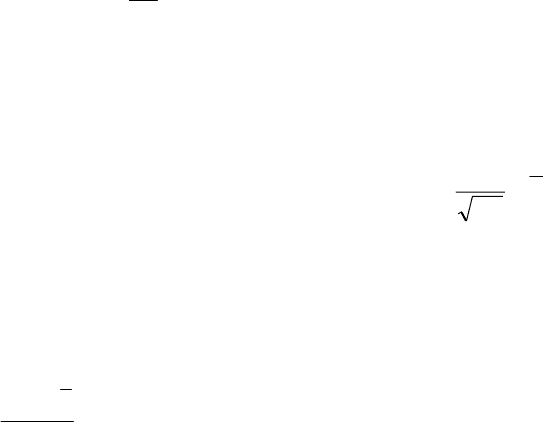
будемо позначати буквою , а теоретично розраховані при гіпотезі нормаль-

ного розподілу – буквою

′

); – центральні значення відповідних класів.

Теоретично передбачені частоти

′

у кожному –му класі

обчислюють за формулою

()

tff

′

, де – обсяг вибірки;

– класовий інтервал;

середнє квадратичне відхилення;

(

)

– функція, яка встановлює орди-

нати нормальної кривої. Для відповідних значень нормованого відхилення

Ця функція, яка має вигляд

()

etf

−

і називається нормованою функцією нормальної густини ймовірності.

Величина

є нормованим відхиленням центрального значення

–го класу від

середнього арифметичного, вираженим у середніх квадратичних відхиленнях:

−

Робота 1. Оцінка істотності належності експериментального розподілу

частот у класах до теоретично відомого стандарту.

Розгляньте приклад і запишіть його у зошит.

Приклад. При схрещуванні двох сортів помідорів, які мали жовті й

червоні плоди, в другому поколінні спостерігали розщеплення ознак у такій

пропорції – 312 червоних і 88 жовтих. Всього було обстежено 400 гібридів.

Чи

відповідає це розщеплення класичному законові Менделя, згідно з яким

ознаки в другому поколінні розщеплюються за пропорцією 3 : 1?

Складемо таблицю з графами, необхідними для обчислення критерію

хі-квадрат (табл. 13). Кількість ступенів вільності

, бо кількість класів

у даному випадку 2, а

−

Таблиця 13

Гібриди

Фактична

кількість

(

)

Теоретично

обчислена

кількість (

′

)

для

співвідношення

3 : 1

ff−

′

(

)

ff−

′

()

−

′

Червоні 312 300 12 144 0,48

Жовті 88 100 12 144 1,44

n = 400 n

400

∑

192,

У табл. 12 [1] знаходимо, що для

граничне значення ,

яке свідчить про істотну різницю в розподілах фактичних (

) і теоретично

очікуваних (

95,0.,

=pтабл

′

) даних, дорівнює 3,84. У нашому випадку .

Гіпотеза про належність характеру розщеплення гібридів в експерименті до

теоретично передбаченого законом Менделя підтвердилась, бо

, а отже різниця в розподілах неістотна.

92,1

експ

95,0.,

pексптабл

χχ

Робота 2. Оцінка істотності належності експериментального розподілу

до нормального.

Розгляньте приклад і запишіть його у зошит.

Приклад. Досліджували діаметри стовбурів сосни (в см) одного віку на

експериментальній ділянці. Проведено 200 обстежень і після вибору

класового інтервалу

дані згрупували у 8 класів

) з частотами , як

це показано в гр. 1–3 (табл. 14).

У гр. 4–7 наведено елементи формул для обчислення середнього

арифметичного

і середнього квадратичного відхилення . Обчислення

елементів для визначення теоретичних частот

′

у класах подано у гр. 8–10.

Для кожного класу обчислюють нормоване відхилення

(гр. 8), за табл. 1 [1]

для кожного

визначають ординати функції густини нормального розподілу

(

)

(гр. 9) і за формулою обчислюють для кожного класу теоретичні частоти

(гр. 10). Для зручності підрахунків емпіричні частоти наводяться у гр. 11

(гр. 11 дублює гр. 3). В тих класах, де кількість частот менша за 5, частоти

′

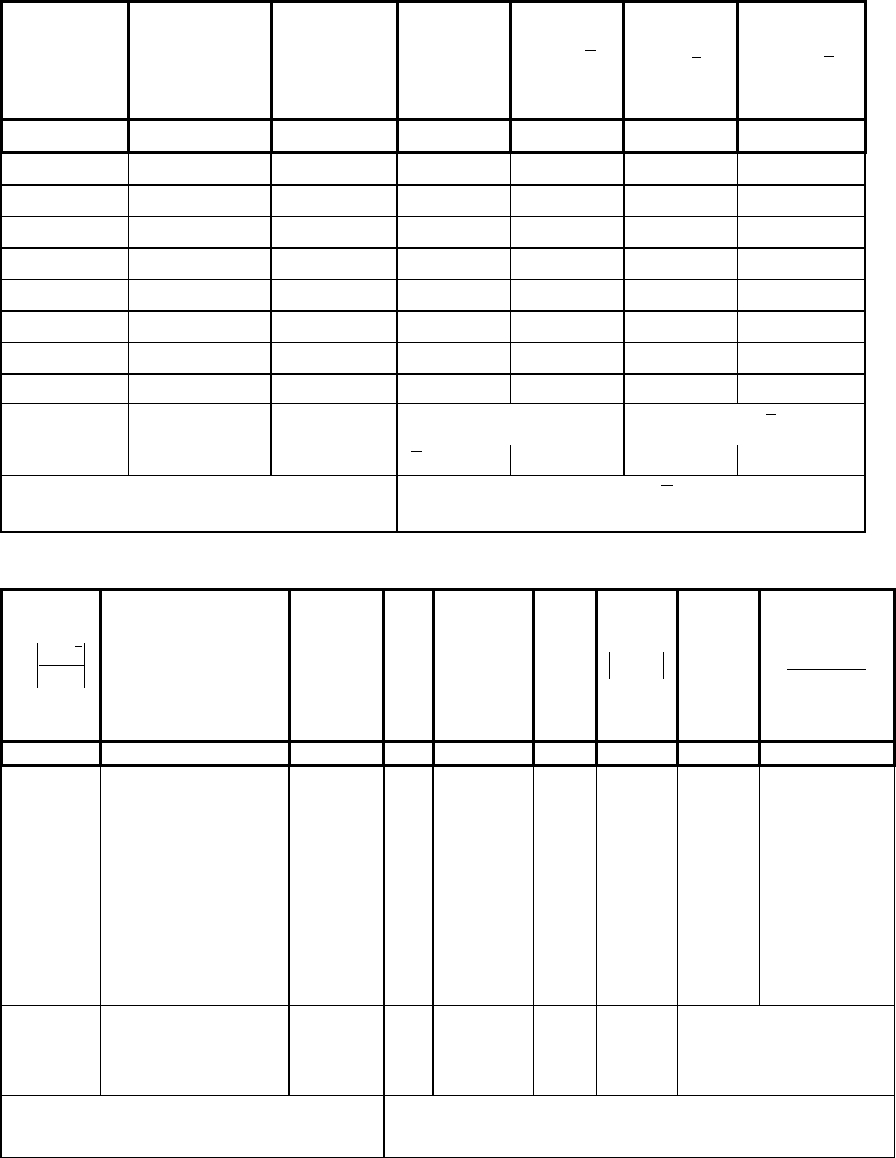
об’єднують з частотами сусідніх класів (гр.10* і 11*), кількість класів за

рахунок об’єднання при цьому зменшується.

Таблиця 14

Класи

Центральні

значення

класів (

)

Фактично

добуті

частоти

(

)

i ц

⋅

−

(

)

−

()

fx x

i ц

−

1 2 3 4 5 6 7

8,1–10,0 9 3 27 –6,76 45,7 137,1

10,1–12,0 11 19 209 –4,76 22,7 431,3

12,1–14,0 1З З1 403 –2,76 7,6 235,6

14,1–16,0 15 49 735 –0,76 0,58 28,4

16,1–18,0 17 57 969 1,24 1,54 87,8

18,1–20,0 19 27 513 3,24 10,5 283,5

20,1–22,0 21 13 273 5,24 27,5 357,5

22,1–24,0 23 1 23 7,24 52,4 52,4

= 8

n = 200

i ц

⋅=

∑

3152

()

6,1613

=−

∑

xxf

љx

= 2

15 76,

= 285,

Класифікація експериментальних

даних

Обчислення

та

−

Функція

нормальної

густини

ймовірності

()

Теоре-

тичні

частоти

′

Емпірич-

ні

частоти

′

−

()

−

′

()

−

′

2,37

1,67

0,024

0,099

22 5 25 1,47

0,97 0,249 35 35 31 31 4 16 0,46

0,27 0,385 55 55 49 49 6 36 0,65

0,44 0,362 52 52 57 57 5 25 0,47

1,14 0,208 29 29 27 27 2 4 0,14

1,84

2,54

0,073

0,016

14 2 4 0,33

n = 200

200

52,3

експ

33 =−= k

Обчислення теоретичних частот у

класах (

)

′

Обчислення

У гр. 12–14 остаточно обчислюють елементи формули хі-квадрат. Сума

величин гр. 14 є значенням

експ

Таким чином, у розглянутому прикладі маємо: ; 52,3

експ

−

;

81,7

95,0.,

=pтабл

, . Отже, гіпотезу про нормальний

розподіл експериментальних вимірів сосни на досліджуваній ділянці

вважаємо доведеною. Відхилити її немає достатніх підстав.

95,0.,

pтаблексп

χχ

Завдання для самостійної роботи

1. У другому поколінні гібридного потомства одержано розщеплення ознак

у пропорції 3050 : 950. Чи відповідає це розщеплення ознак закону

Менделя (3 : 1)? Яка величина критерію

? Яка кількість ступенів

вільності

2. Як видно з наведеної нижче таблиці, теоретична лейкоцитарна формула

при захворюванні А і лейкоцитарна формула хворого дещо відрізняються:

Дані, % Базофіли Еозинофіли Нейтрофіли Лімфоцити Моноцити

Тип А – 10 50 25 15

Хворий 2 5 45 30 18

Чи можна віднести лейкоцитарну формулу хворого до типу хвороби А? Яка

величина критерію

? Яка кількість ступенів вільності

3. У другому поколінні нового гібрида очікують розщеплення ознак згідно з

законом Менделя (3 : 1). В експерименті дістали розщеплення потомства

гібрида в частотній пропорції 72 : 48. Чи підтверджує цей дослід закон

Менделя? Яке значення критерію

4. Теоретично передбачається, що вага кроликів породи А розподіляється за

біноміальним законом так, як це показано в наведеній нижче таблиці.

Фактичний розподіл дещо відрізняється від теоретично передбаченого.

Одержані дані унормовано за загальною кількістю (n

теор.

= n

експ.

)

Класи,

кг

Частоти 1,0—1,9 2,0—2,9 3,0—3,9 4,0—4,9 5,0–5,9 6,0–6,9 7,0—7,9

Теор. ( ).

′

3 21 52 69 52 21 3

Експ. ( )

1 13 60 73 42 30 2

Чи відповідає експериментальне одержаний розподіл частот теоретично

передбаченому? Чому дорівнює величина

? Яка кількість ступенів

вільності

5. У другому поколінні гібрида при дигібридному схрещуванні одержано

розщеплення ознак за такою пропорцією частот (кількість гібридних

рослин з відповідними ознаками):

Ознака

+ + + — — + — —

Частота

92 26 35 7

Чи відповідає це розщеплення законові Менделя (теоретичне розщеплення

9 : 3 : 3 : 1)? Яка величина критерію

? Яка кількість ступенів вільності

6. При схрещуванні довгошерстих овець із звичайними вівцями в другому

поколінні було одержано 180 овець, з яких 82 були довгошерстими, а 98

мали звичайну шерсть. Чи відповідає це відношенню 1 : 1? Чому дорівнює

7. При проведенні серії визначень віку популяції полівок в дослідному

регіоні були одержані такі дані щодо розподілу особин у вікових класах:

Класи

1–2 3–4 5–6 7–8 9–10 11–12 13–14 15–16 17–18 19–20

Частота ( )

6 4 10 18 25 16 9 4 2 1

Чи можна віднести цей розподіл до типу нормального? Яке значення при

гіпотезі нормального розподілу?

Література

1. Зінченко О. П. Методичні матеріали для проведення лабораторних і

практичних занять з курсу “Математичні методи в біології (Статистичні

таблиці) / О. П. Зінченко, В. П. Бенедь.– Луцьк: ВДУ, 1995.– Ч. 1.– 39 с.

2. Лакин Г. Ф. Биометрия / Г. Ф. Лакин.– М.: Высш. школа, 1990.– C. 138-145.

3. Терентьев П. В. Практикум по

биометрии / П. В. Терентьев, Н. С. Ростова.–

Л.: Изд-во Ленингр. ун-та, 1977.– C. 50-57.

Лабораторна робота №13

Тема: Оцінка характеру розподілу. Розв'язання прикладів на

біноміальний закон розподілу, закон розподілу Пуассона. Порівняння за

характером розподілу.

Мета: Навчитись оцінювати характер розподілу за даними вибірки.

Оволодіти методикою розв’язання прикладів на біноміальний закон

розподілу, закон розподілу Пуассона та за характером розподілу.

Матеріал і обладнання: калькулятори,

комп’ютери, розрахункові

таблиці.

Контрольні питання:

1. Біноміальний розподіл.

2. Розподіл Пуассона

3. Порівняльна оцінка істотності різниці в характері двох

експериментальних розподілів.

Інформаційний матеріал

Біноміальний розподіл.

Нормальний розподіл неперервний за своїм характером, тобто окремі

варіанти у варіаційному ряді, наприклад значення зросту або ваги, можуть

набувати будь-яких значень у межах

біологічної мінливості даної ознаки.

Біноміальний розподіл перервний (дискретний) за своєю природою, отже,

його застосовують при статистичній обробці дискретних сукупностей і

біологічних явищ. Для наочності можна сказати, що біноміальний розподіл

спостерігається тоді, коли підраховують кількості поодиноких подій, а

нормальний – коли беруть відліки з вимірювального приладу.

Якщо позначити ймовірність здійснення поодинокої дискретної

події

буквою

, а ймовірність її нездійснення – буквою (очевидно, що

p q

−

1 ),

то залежно від того, наскільки близькі

і , біноміальний розподіл

p q

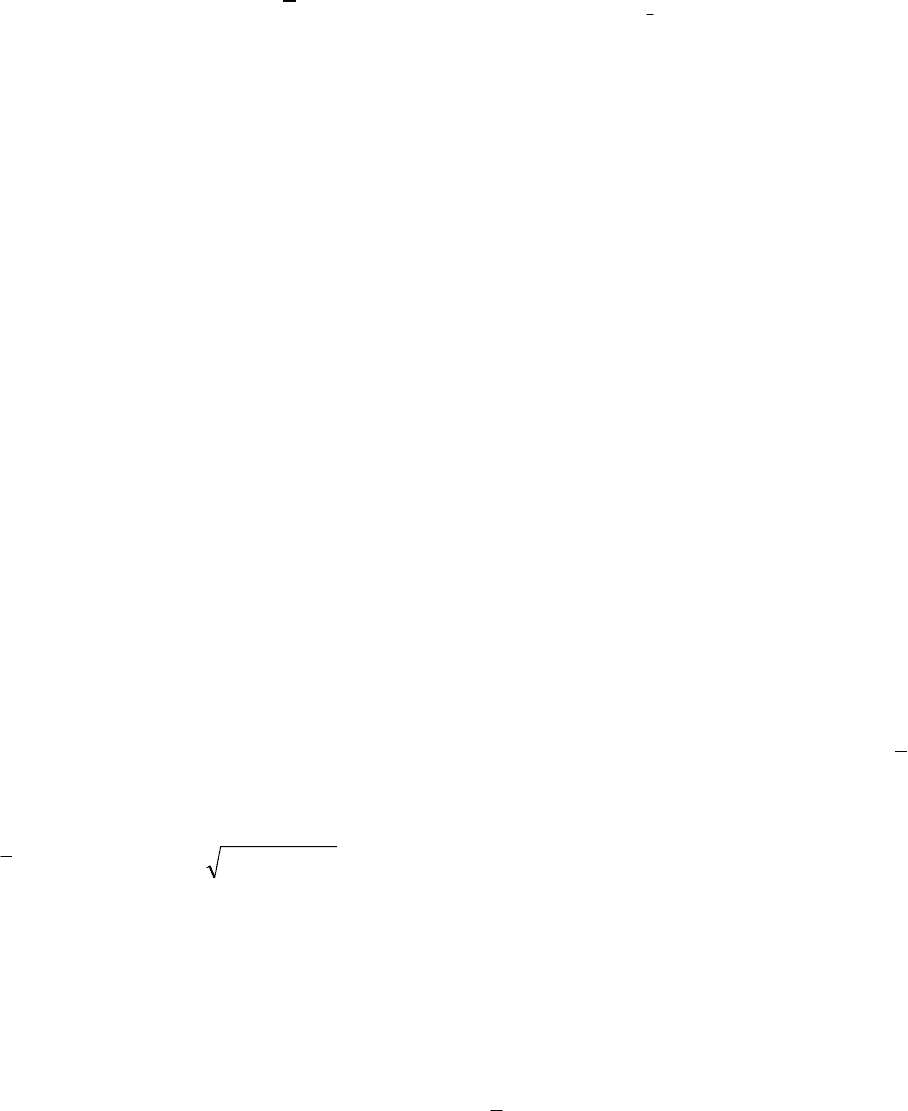
проявлятиме більшу або меншу симетрію. Для біологів особливо цікавий

біноміальний розподіл подій, коли

≈

Як і нормальний розподіл, він тоді буде симетричним відносно

середнього значення. Аналогічний зміст для обох розподілів мають середнє

арифметичне значення

, його стандартна похибка

і середнє квадратичне

відхилення

Наведемо приклад. Ймовірності позитивного і негативного ефекту під

час запліднення яйцеклітин у самок гризунів близькі

(

)

pq≈

. Отже, кількість

народжених малят у сукупності пар мишей розподіляється за біноміальним

законом. Ймовірність формування жіночої й чоловічої статей під час

запліднення яйцеклітин однакова

(

)

pq≈

, тому кількість самок у сукупності

однакових (наприклад по 10 шт.) серій яєць курей також підлягає

біноміальному закону. До біноміального розподілу належать розподіли

кількостей дітей за статтю в сім'ях, зерен у колосках злаків, клітин у полі

зору мікроскопа тощо. В усіх згаданих явищах класами є кількості певних

дискретних (неподільних) подій або

ознак – дітей, яєць, листків, зерен,

ікринок, клітин, вакуолей тощо.

Для біноміального розподілу існує свій математичний апарат

обчислення статистичних показників. Зокрема, якщо кількість класів, на які

розпадається сукупність, позначити буквою

, то середнє арифметичне

середнє квадратичне відхилення

можна обчислити за формулами

()

xk=−1 p

та

()

Skp

=−⋅⋅1 q

Розподіл називається біноміальним, оскільки пропорції частот у класах,

на які розпадається сукупність, тобто ймовірності появи подій даного класу,

відповідають співвідношенню коефіцієнтів при розкладенні бінома Ньютона.

Ці коефіцієнти (

бні .

) – наведено в табл. 4 [1]. Треба звернути увагу, що в

посібниках статистики в обох формулах

і стоїть величина

, а не (

−

1).

Насправді розбіжності тут немає, оскільки в літературі прийнято буквою

позначати так зване число незалежних випадкових явищ, що збігається з

показником ступеня бінома Ньютона, а у нас

– це кількість класів, тобто

величина, яку легше зрозуміти при вивченні матеріалу.

Розподіл Пуассона.

Біноміальний розподіл справедливий для явищ, у яких імовірності

здійснення і нездійснення події близькі; ця властивість зумовлює його

симетричність. Коли досліджують рідкісні події в сукупності тривіальних

(звичайних) подій, а отже, ймовірності перших дуже малі порівняно з

другими

(

, то біноміальний розподіл стає істотно асиметричним. Серед

такого роду асиметричних розподілів найбільше значення має розподіл

Пуассона.

)

pq<<

Розподіл Пуассона, як і біноміальний, є розподілом дискретних подій.

Він трапляється, наприклад, у статистичному аналізі вимірів радіоактивності

(кількість ядер, що розпадаються за одиницю часу, значно менша порівняно з

кількістю ядер, які не розпалися

), смертності в статистичних колективах

(імовірність смерті в мікрорайоні – відносно рідкісна подія), народження

близнят у пологовому будинку за певний проміжок часу, кількості мутантних

клітин у колонії опромінених мікроорганізмів тощо.

Схема досліду полягає в тому. що фіксують певний інтервал часу або

простору і на цьому проміжку реєструють кількість появи досліджуваних

подій. Кількість

проведених дослідів повинна бути достатньо великою

(

). Розподіл Пуассона характеризується рядом властивостей, які дають

змогу розпізнати його серед інших статистичних розподілів:

n > 50

1) дискретність подій;

2) рідкісність появи досліджуваних подій;

3) середнє арифметичне

і дисперсія рівні або близькі за своїми

числовими значеннями:

Sx =

Коли ці властивості спостерігаються в експерименті, є всі підстави

висунути гіпотезу про те, що сукупність підлягає закону – розподілу

Пуассона і перевірити статистичну істотність цієї гіпотези методом хі-

квадрат.

Перевірку гіпотези про належність експериментальної вибірки до типу

розподілу Пуассона починаємо з обчислення теоретично передбачених

частот у класах

. Їх обчислюємо для кожного класу за формулою

′

⋅

−

де

– основа натуральних логарифмів (

2 7183, ...

);

– середнє

арифметичне;

– число класів досліджуваної події (

, а для класів з

значення v!.=⋅⋅⋅ v...

⋅

122 ). Величину

xv−

⋅

називають функцією

Пуассона; позначимо її

Пуас.

. Отже,

′

⋅

i Пуас

Перевірка гіпотез для порівняння між собою двох

експериментальних розподілів.

Метод хі-квадрат можна застосовувати не тільки для перевірки гіпотез

про належність експериментального розподілу частот до певного

теоретичного типу (еталонного розподілу частот), але також і для порівняння

між собою двох експериментальних розподілів.

Формула критерію хі-квадрат при порівнянні між собою двох

експери-

ментальних розподілів має такий вигляд:

(

)

12 21

⋅

−

∑

nf nf

, де і f

частоти в класах першої і другої експериментальних серій:

і відповідно

обсяг сукупності в кожній із серій.

Для того щоб стверджувати, що розподіли в обох серіях різні, обчислене

експериментальне значення хі-квадрат повинно бути більшим за граничне

значення хі-квадрат у табл. 12 [1] для

095, .

Робота №1. Оцінка істотності належності експериментального

розподілу частот до біноміального розподілу.

Розгляньте приклад і запишіть його у зошит.

Приклад. Було обстежено 100 приплодів свиней породи А (табл. 15).