Журнал - Проблемы криобиологии 2010 №4

Подождите немного. Документ загружается.

419

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

Такой же вид имеет зависимость для расчета

плотности водных растворов NaCl и CaCl

, а

также смесей криопротекторов. Значения коэф-

фициентов b

÷b

полинома (2) для водных раст-

воров NaCl и CaCl

, водных растворов ряда крио-

протекторов и их смесей представлены в табл.

2–5. Коэффициенты b

÷b

имеют размерность

кг/м

Кроме коэффициентов полиномов в таблицах,

представлены дисперсии аппроксимации, диапа-

зоны применимости уравнений (температура или

концентрация) и источники литературы, из ко-

торых взяты экспериментальные данные. Диа-

пазон применимости уравнений показывает, при

каких температурах или при каких концентрациях

были получены экспериментальные данные,

приведенные в статьях. При вычислениях этот

диапазон может быть расширен без сущест-

венной потери точности, особенно для линейных

уравнений, описываемых полиномом первой

степени. В таблицах приняты следующие услов-

ные обозначения:

БД – бутандиол;

ГОЭК – гидроксиэтилкрахмал;

ДМАц – диметилацетамид;

ДМСО – диметилсульфоксид;

ДМФА – диметилформамид;

ДЭГ – диэтиленгликоль;

М – мальтодекстрин;

МАц – метилацетамид;

МФА – метилформамид;

МХГГ – монохлоргидрин глицерина;

ОЭГ – оксиэтилированный глицерин;

ПВП – поливинилпирролидон;

ПД – пропандиол;

ПЭГ – полиэтиленгликоль;

ПЭО – полиэтиленоксид;

ТЭГ – триэтиленгликоль;

ФА – формамид;

ЭГ – этиленгликоль.

Данных по кинематической вязкости криопро-

текторов и их растворов в доступной литературе

чрезвычайно мало. Однако кинематическая вяз-

кость ν может быть определена как отношение

динамической вязкости µ жидкости к плотности

ρ этой жидкости: ν = µ/ρ.

Данные по динамической вязкости криопро-

текторов и их водных растворов можно получить

из [20], а данные по плотности приведены выше.

Кинематическая вязкость ν имеет размерность

сантистокс (1 сСт = 10

–6

/с).

Для воды и чистых криопротекторов зависи-

мость кинематической вязкости от температуры

описывается полиномом:

ν = c

+ c

t + c

. (3)

cryoprotectant solutions on temperature has the same

dependence, described only with the polynomial of the

second degree.

To determine the density of cryoprotectant aque-

ous solutions depending on their mass concentration

there is used the polynomial equation:

ρ = b

+ b

C + b

, (2)

where C – mass concentration of the cryoprotective

agent, %.

The same appearance has the dependence for cal-

culation density of aqueous solutions of NaCl and

CaCl

, as well as the mixtures of cryoprotective agents.

The values of coefficients b

÷b

of polynomial (2) for

aqueous solutions of NaCl and CaCl

, aqueous solu-

tions of some cryoprotective agents and their mixtures

are given in the Tables 2–5. Coefficients b

÷b

have

the dimensions of kg/m

Except the polynomial coefficients there are pre-

sented in tables the approximation dispersion, applica-

tion range of equations (temperature and concentra-

tion) and literature sources wherefrom the experimental

data are derived. The application range of equations

shows under what temperatures and concentrations

the experimental data, presented in the papers were

obtained. During calculation this range may be extended

without significant loss of accuracy, especially for lin-

ear equations, described with the polynomial of the

first degree.

The following symbols are shown in the tables:

BD – butane diol

HES – hydroxiethyl starch

DMAc – dimethyl acetamide

DMSO – dimethyl sulfoxide

DMFA – dimethyl formamide

DEG – diethylene glycol

M – maltodextrin

MAc – methyl acetamide

MFA – methyl formamide

MChHG – monochlohydrin glycerol

OEG – oxyethylated glycerol

PVP – polyvinylpyrrolidone

PD – propane diol

PEG – polyethylene glycol

PEO – polyethylene oxide

TEG – triethylene glycol

FA – formamide

EG – ethylene glycol.

The data for kinematic viscosity of cryoprotective

agents and their solutions in the available literature is

extremely insufficient. However kinematic viscosity ν

may be determined as ratio between of dynamic vis-

cosity of fluid, µ, and its density: ν = µ/ρ.

The data for dynamic viscosity of cryoprotective

agents and their aqueous solutions can be obtained from

овтсещеВ

ecnatsbuS

,арутарепмеТ

C°

,erutarepmeT

C°

, × 01

нозапаиД

йицартнецнок

%.ссам,С

noitartnecnoC

)w/w(%,egnar

кинчотсИ

ecnerefeR

lCaC

6,510886,4339,71,9999999,00÷ 03]53[

020 637,45820,83,89910÷ 04]45[

lCaN

51369,33065,0963,71,99910÷ 52

,84,71,01[

]06,95,25

020 643,220,72,89910÷ 03

52818,1-153,3355,71,79910÷ 06

овтсещеВ

ecnatsbuS

,яицартнецноK

%.ссам

,noitartnecnoC

)w/w(%

, × 01

нозапаиД

C°,рутарепмет

erutarepmeT

C°,egnar

кинчотсИ

ecnerefeR

нирецилГ

lorecylG

05614,4-556,4-63113649,003- ÷ 06

,44,61,41,21,01[

]28,47,37

лонатеМ

lonahteM

040 884,5-98,5499999,00÷ 021]21[

ГЭ

0577,51-839,5-57012899,002- ÷ 52]56,3[

лонатЭ

lonahtE

02497,6-219,4-2,879999,00÷ 021

]21[

04193,1-1,6-2,7499999,00÷ 021

06288,4-814,6-4098999,00÷ 021

08406,0-124,7-7,7587999,00÷ 021

420

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

Значения коэффициентов c

÷c

полинома (3)

для воды и ряда криопротекторов представлены

в табл. 6. Для соблюдения размерности прини-

мается: с

– сСт×°С

–5

, с

– сСт×°С

–4

, с3 –

сСт×°С

–3

, с

– сСт×°С

–2

, с

– сСт×°С

–1

, с

– сСт.

Подобную зависимость, определяемую полино-

мом третьей степени, имеет кинематическая вяз-

кость водных растворов NaCl и раствора Ринге-

ра-Локка (табл. 7).

Кинематическая вязкость водных растворов

криопротекторов в зависимости от их массовой

концентрации описывается полиномиальным

уравнением:

ν = d

+ d

C + d

, (4)

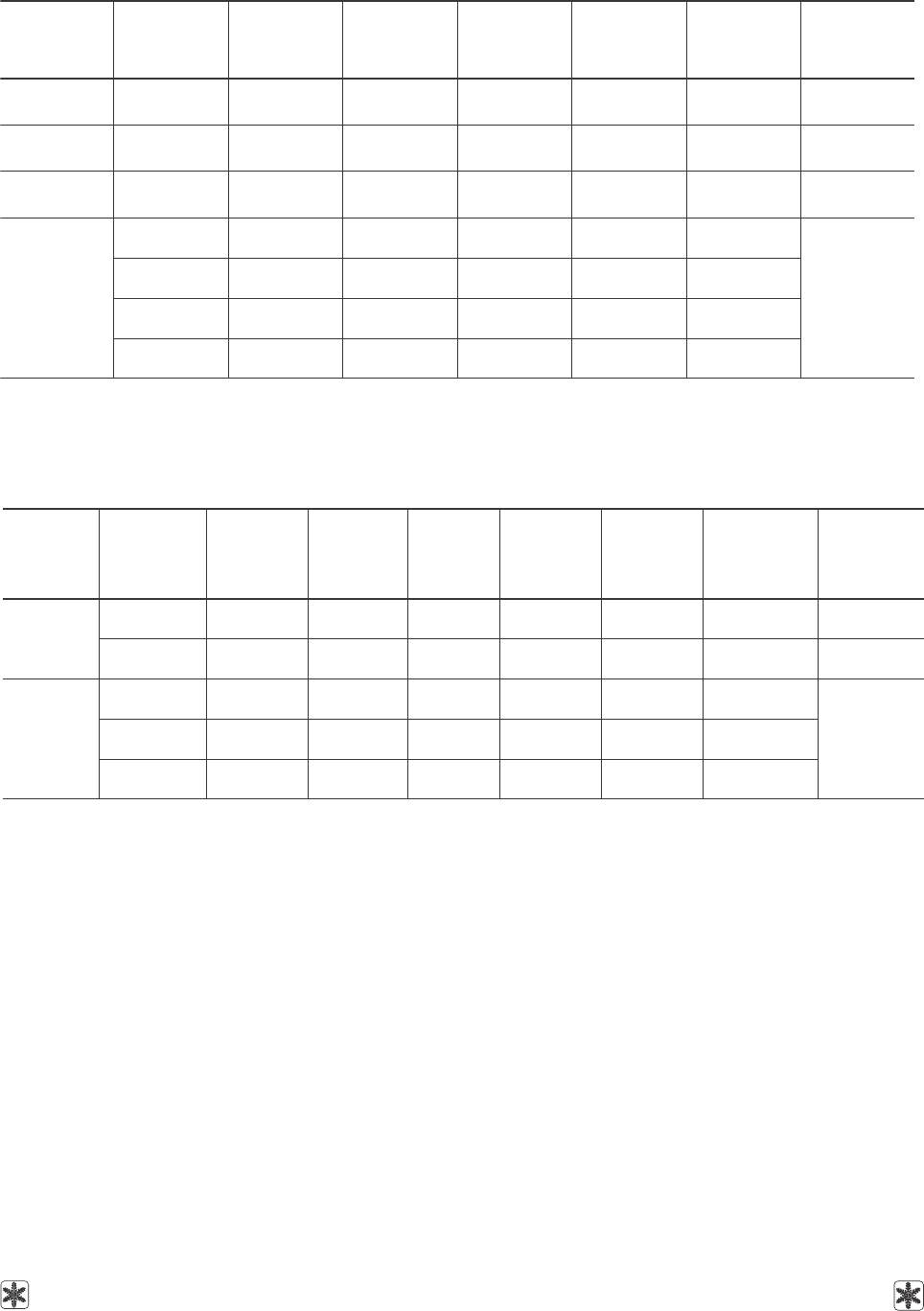
Таблица 3. Коэффициенты уравнения (2) для расчета плотности водных растворов NaCl

и CaCl

в зависимости от концентрации при заданной температуре; дисперсии

аппроксимаций и диапазоны концентраций применения уравнения

Table 3. Coefficients of equation (2) to calculate the density of NaCl and CaCl

aqueous solutions depending on

concentration at given temperature; approximation dispersion and concentration ranges of equation application

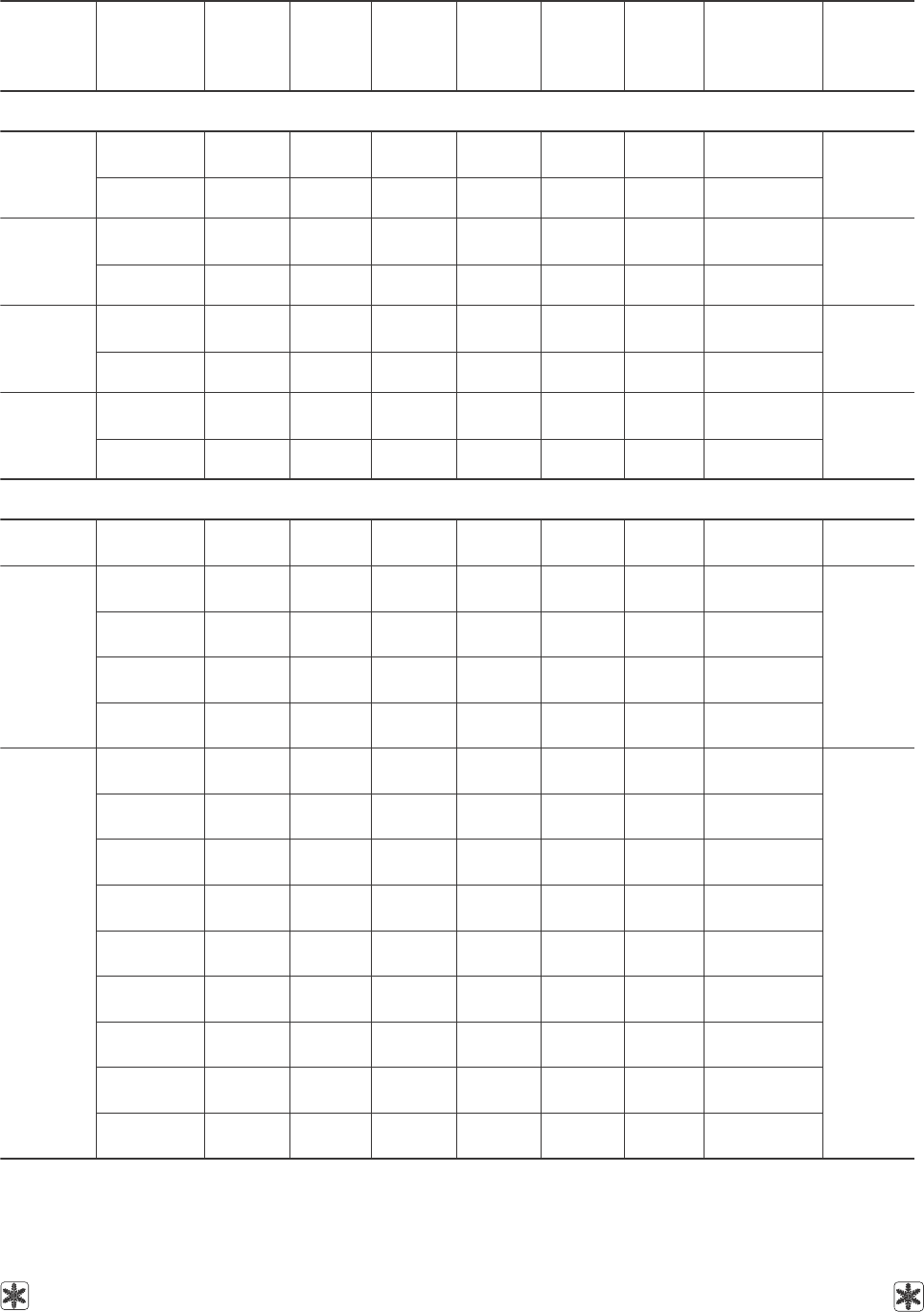
Таблица 2. Коэффициенты уравнения (1) для расчета плотности ряда водных растворов криопротекторов

при заданной концентрации в зависимости от температуры; дисперсии аппроксимаций

и диапазоны температур применения уравнения

Table 2. Coefficients of equation (1) to calculate the density of cryoprotective agents’ some aqueous solutions at given

concentration depending on temperature; approximation dispersion and temperature ranges of equation application

[20], but the data for density are shown above. The ν

kinematic viscosity has centistoke dimension (1 cSt =

–6

/s)

The dependence of kinematic viscosity on tempera-

ture for water and pure cryoprotective agents is de-

scribed with polynomial:

ν = c

+ c

t + c

. (3)

The values of c

÷c

polynomial coefficients (3) for

water and some cryoprotective agents are presented

in Table 6. To keep the dimensions it is assumed that:

– cSt×°С

–5

, с

– cSt×°С

–4

, с3 – cSt×°С

–3

, с

–

cSt×°С

–2

, с

– cSt×°С

–1

, с

– cSt. Kinematic viscosity

of NaCl aqueous solutions and Ringer-Lock solution

has the same dependence, determined only with the

polynomial of the third degree (Table 7).

овтсещеВ

ecnatsbuS

,арутарепмеТ

C°

,erutarepmeT

C°

, × 01

нозапаиД

йицартнецнок

%.ссам,С

noitartnecnoC

)w/w(%,egnar

кинчотсИ

ecnerefeR

sedimAыдимА

цАМД

cAMD

52562,3-25,32838,0-890,2-1,7998999,00÷ 001

]74[

53191,3-185,3910,1-733,3-1,4999999,00÷ 001

АФМД

AFMD

525605,0382,2-205,168,52-1,7997999,00÷ 001

]74,11[

532951,0425,1-830,12,72-4998999,00÷ 001

анивечоМ

aerU

02004555,05,0622,8999999,00÷ 05

]67,86,45[

52005534,05,2621,7990,10÷ 04

АФМ

AFM

521096,0427,1-4386,084,631,7995999,00÷ 001

]74,11[

536507,0638,1-5948,019,321,4992999,00÷ 001

sremylopelbulosretaWыремилопеымировтсародоВ

нартскеД

nartxeD

020008,7831,8997999,00÷ 01]45[

ПВП

)00001.в.м(

PVP

)00001.w.m(

520 721,2-558,17,4811,799999,00÷ 05

]06,73[

530421,9893,5-7,8721,4994299,00÷ 05

540187,8443,5-2,4723,0991899,00÷ 05

5501,21713,7-1,0927,5899699,00÷ 05

ГЭП - 004

GEP - 004

520 462,1-220,12,8411,7998999,00÷ 001

]86,24,43[

720 291,1-779,01,5415,6999999,00÷ 001

030 161,1-9888,09,8417,5998999,00÷ 001

530 541,1-1788,01,5411,4998999,00÷ 001

730 932,1-750,13,7313,3998999,00÷ 001

040 951,1-8139,07,9312,2999999,00÷ 001

540 301,1-2578,08,7313,0998999,00÷ 001

050 860,1-8938,01,6311,8898999,00÷ 001

550 880,1-988,09,2317,5898999,00÷ 001

421

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

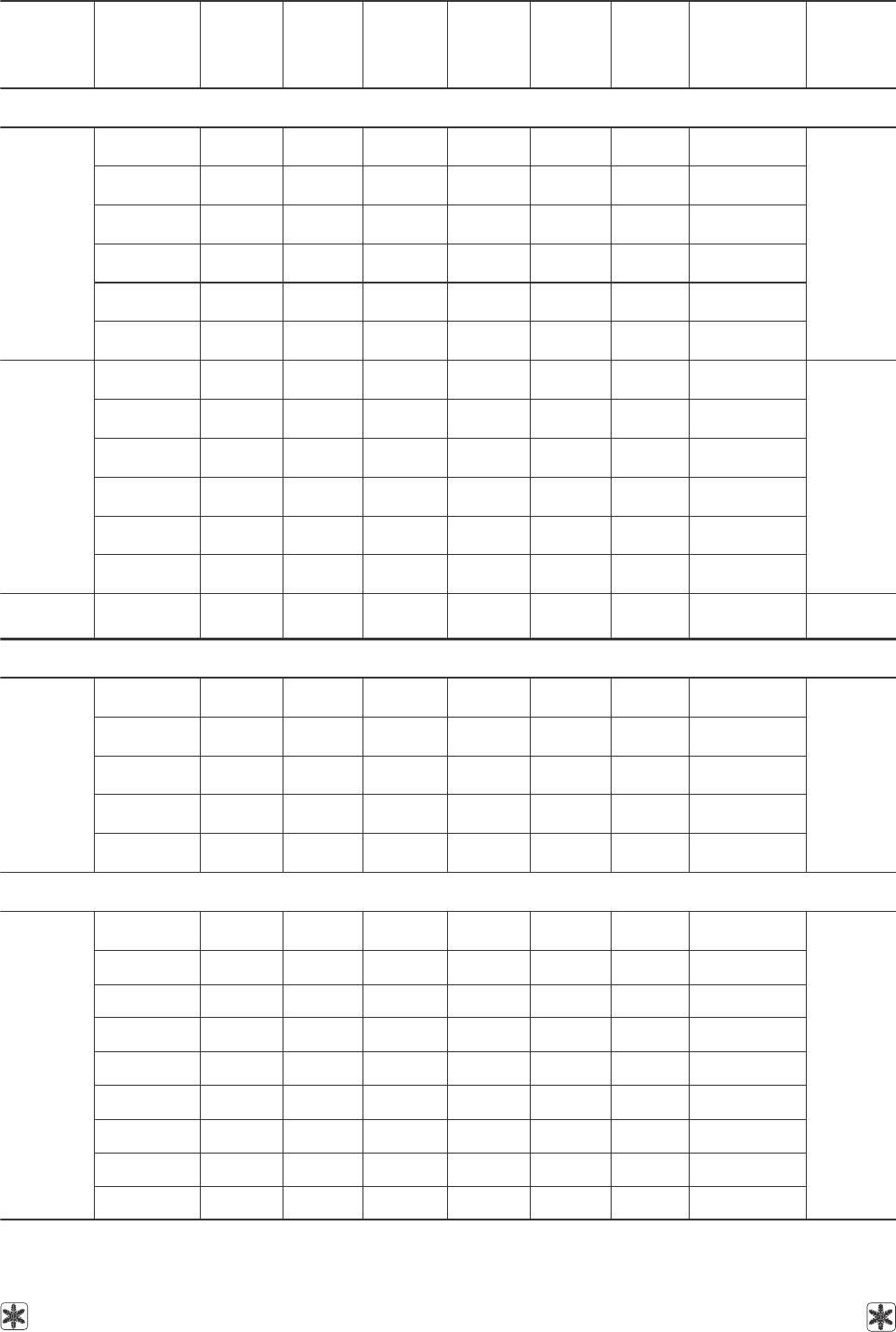
Таблица 4. Коэффициенты уравнения (2) для расчета плотности ряда водных растворов

криопротекторов в зависимости от концентрации при фиксированных температурах;

дисперсии аппроксимаций и диапазоны концентраций применения уравнения

Table 4. Coefficients of equation (2) to calculate the density of some aqueous cryoprotective agents depending on

concentration at fixed temperatures; approximation dispersion and concentration ranges of equation application

Продолжение на следующей странице.

Next page to be continued.

овтсещеВ

ecnatsbuS

,арутарепмеТ

C°

,erutarepmeT

C°

, × 01

нозапаиД

йицартнецнок

%.ссам,С

noitartnecnoC

)w/w(%,egnar

кинчотсИ

ecnerefeR

sremylopelbulosretaWыремилопеымировтсародоВ

ГЭП - 0004

GEP - 0004

7200198,09,0415,6995499,00÷ 04

]43[

73002037,03,9313,399699,00÷ 04

04008995,01,3412993599,00÷ 04

5400585,08,9313,0998599,00÷ 04

05004554,01,2417,7899599,00÷ 04

55002914,00417,5893599,00÷ 04

ГЭП - 0006

GEP - 0006

72008473,07,0615,6996999,00÷ 04

]43[

73007123,02,6513,3998999,00÷ 04

04008952,02,7512996999,00÷ 04

54004452,09,25152,0995999,00÷ 04

05007402,05,1518,7896899,00÷ 04

55003934,01,9317,5897799,00÷ 04

ГЭП - 0008

GEP - 0008

5200 610,0-9,4711,7999999,00÷ 04]86[

sedixOыдискО

ОСМД

OSMD

02088,1-577,16,8012,8992799,00÷ 001

,26,15,23,72[

]09,38,47,66

4200 744,0-3,64123,7993989,00÷ 001

520 917,1-736,12,6011,7996999,00÷ 001

540 565,1-644,197,6952,0997999,00÷ 001

560 32,41-172,169,986,0896999,00÷ 001

slohoclAытрипС

нирецилГ

lorecylG

03-00 367,0-3,2739,3895999,003 ÷ 07

,44,41,21,01[

]67,76,45,84

02-00 231,0-3,0136,3995799,002 ÷ 08

01-00 80,0-2,2921,8995899,001 ÷ 08

5-00 8660,07,3723,9996999,003 ÷ 08

000 2839,01,62258,9994599,00÷ 06

51007971,09,9421,9998999,00÷ 001

02001902,06,4422,8995999,00÷ 001

52006132,03,0421,7998899,00÷ 001

03001902,08,0426,5998999,00÷ 001

422

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

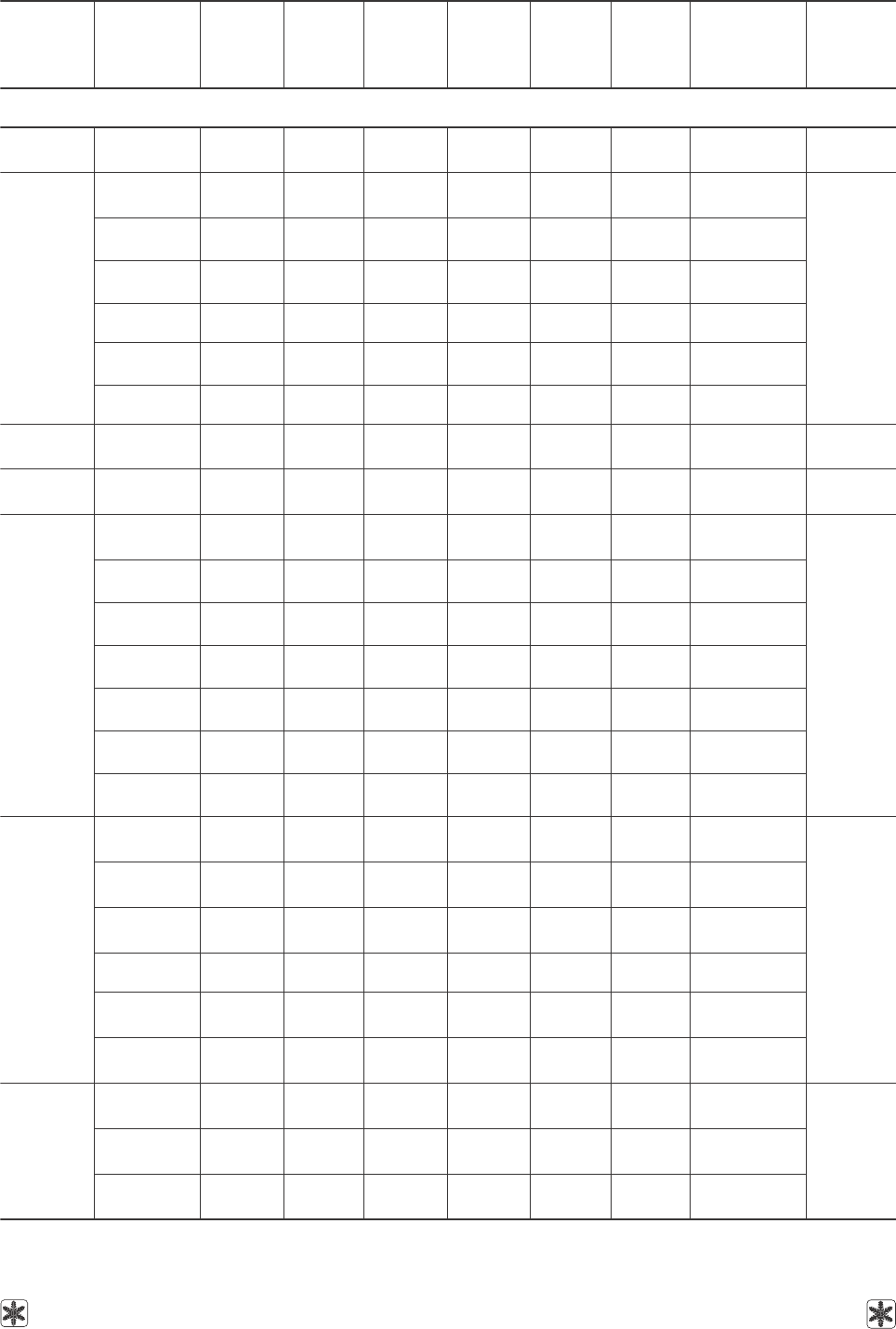
Продолжение табл. 4

Table 4. (Continued from the previous page)

Продолжение на следующей странице.

Next page to be continued.

овтсещеВ

ecnatsbuS

,арутарепмеТ

C°

,erutarepmeT

C°

, × 01

нозапаиД

йицартнецнок

%.ссам,С

noitartnecnoC

)w/w(%,egnar

кинчотсИ

ecnerefeR

slohoclAытрипС

тиннаМ

etinnaM

0200430,12,7432,8999999,00÷ 51]45[

лонатеМ

lonahteM

00 815,0-241,0-8,421-8,9994999,00÷ 001

,85,45,63,21[

]98,88,57

01094,0-21,0-6,831-6,9997999,00÷ 001

510 845,0-620,0-5,741-1,9997999,00÷ 001

02064,0-580,0-7,151-2,8996999,00÷ 001

520 724,0-01,0-7,951-1,7996999,00÷ 001

030 913,0-892,0-8,551-6,5998999,00÷ 001

лонапорП

lonaporP

52053,86393,1-121-1,7996999,00÷ 001]98[

тиброС

lotibroS

5200 986,0-4,5731,7999999,00÷ 04]19[

ГЭТ

GET

8,71-0084,0-94,4719,03010,105 ÷ 09

]28[

010092,0-23,2511,11010,101 ÷ 001

8,730055,0-57110,1990,101 ÷ 001

6,560044,0-59,35124,9790,101 ÷ 001

3,390053,0-45,04147,1690,101 ÷ 001

1,1210082,0-29,13163,0490,101 ÷ 001

9,8410012,0-89,42187,6190,101 ÷ 001

ГЭ

01-00 455,0-5,4911,8999899,00÷ 05

45,25,52,3[

]86,56

5-00 63,0-8,6713,9993999,00÷ 05

6,5100703,0-2,2713,4996999,052 ÷ 56

0200 932,0-9,9312,8999799,00÷ 001

5200 66310,07,8211,7997999,00÷ 05

7,62002,0-0,6512,5996999,052 ÷ 56

лонатЭ

lonahtE

6,5100838,0-5,221-1,9993999,00÷ 001

,05,63,21,01[

,38,57,47,65

]98

0200 287,0-8,031-2,899999,00÷ 001

5200 637,0-9,531-1,7998899,00÷ 001

423

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

Продолжение табл. 4

Table 4. (Continued from the previous page)

Продолжение на следующей странице.

Next page to be continued.

овтсещеВ

ecnatsbuS

,арутарепмеТ

C°

,erutarepmeT

C°

, × 01

нозапаиД

йицартнецнок

%.ссам,С

noitartnecnoC

)w/w(%,egnar

кинчотсИ

ecnerefeR

slohoclAытрипС

2,1 - ДП

2,1 - DP

4,4045,1-847,06,21100018899,002 ÷ 56

]29,45,62[

6,510890,1-726,026,199995899,002 ÷ 56

02058,0-974,04,472,8996899,00÷ 001

030 807,0-972,072,577,5992799,00÷ 001

040 107,0-472,015,172,2999699,00÷ 001

050 386,0-252,035,761,8892699,00÷ 001

06076,0-7932,053,462,3897599,00÷ 001

070 166,0-432,070,268,7793599,00÷ 001

080 646,0-22,021,958,1797499,00÷ 001

setardyhobraCыдовелгУ

азокюлГ

esoculG

0203264,0441,14,2832,8990,10÷ 06

]86,95,45,01[

520080,36,2531,7998999,00÷ 52

азолисK

esolyX

520043,1-6,5631,7990,10÷ 04]68[

азоткаЛ

esotcaL

020 963,3-184,15,3932,899899,00÷ 62

]45,35[

5200079,0931,7993599,00÷ 51

азотьлаМ

esotlaM

0200966,11,0832,8990,10÷ 06

]68,45[

5200 272,1-3,9831,7990,10÷ 08

азорахаС

esorcuS

5100383,22531,9998899,00÷ 001

,84,14,01[

,65-45

]67,86

020988,1431,0-3,4142,899999,00÷ 001

5200223,16,0931,7998999,00÷ 04

0300287,17,2736,5991999,00÷ 06

0600 770,1-6,3666,5093289,005 ÷ 001

азолагерТ

esolaherT

02048,2816,03-8,6962,8999639,00÷ 52]78[

азоткурФ

esotcurF

0201282,0213,18,9832,8990,10÷ 56]45[

424

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

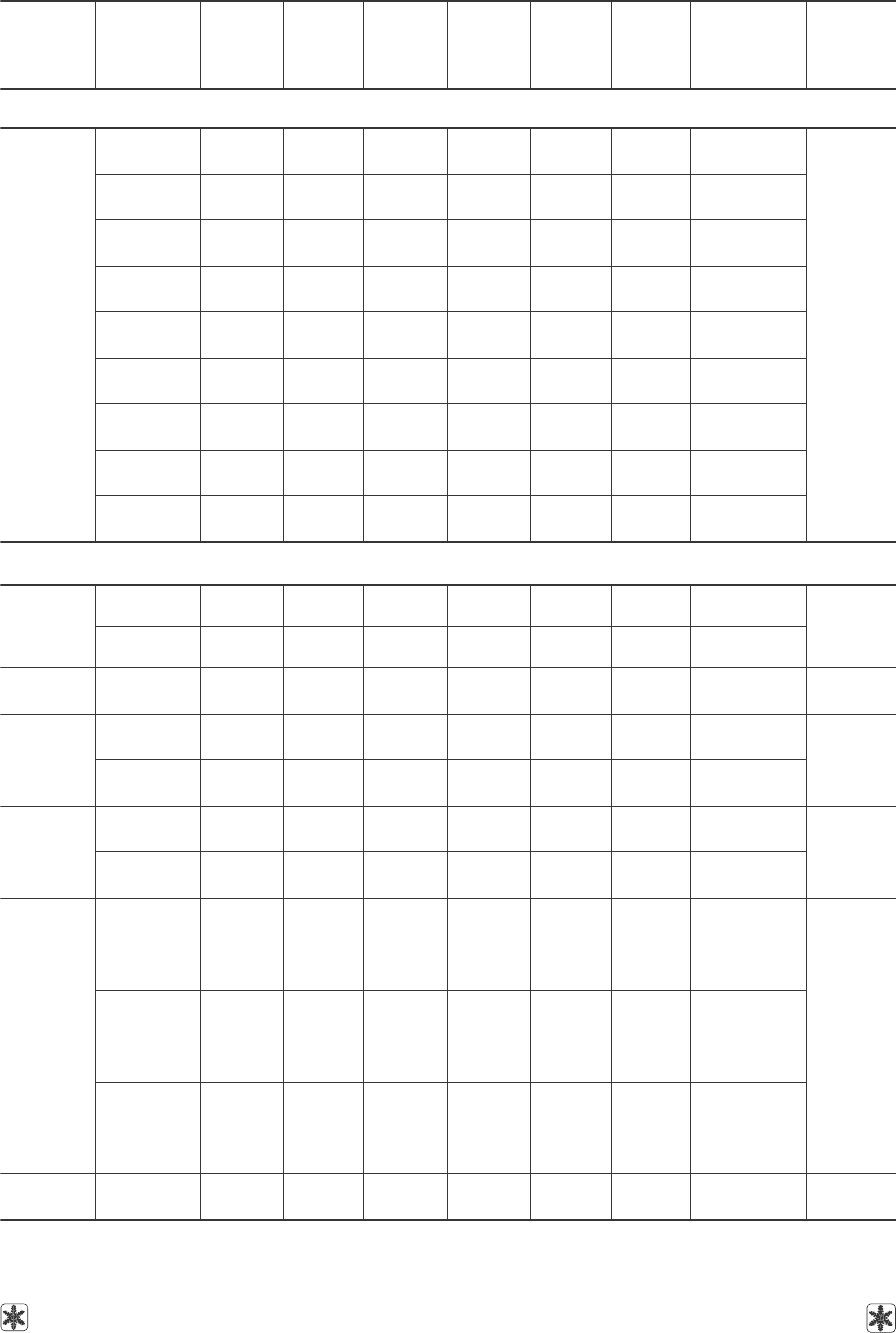
Продолжение табл. 4

Table 4. (Continued from the previous page)

овтсещеВ

ecnatsbuS

C°,арутарепмеТ

C°,erutarepmeT

, × 01

нозапаиД

йицартнецнок

%.ссам,С

noitartnecnoC

)w/w(%,egnar

кинчотсИ

ecnerefeR

азокюлГ

esoculG

52760,5547,35,59010,10÷ 53

]07[

53266,3118,35,58010,10÷ 53

54852,5797,37,57010,10÷ 53

55363,4648,37,56010,10÷ 53

азорахаС

esorcuS

52414,8776,35,59010,10÷ 04

]07[

53901,996,35,58010,10÷ 04

54992,9807,37,57010,10÷ 04

55725,8577,37,56010,10÷ 04

азоткурФ

esotcurF

52642,6335,35,59010,10÷ 04

]07[

53326,6445,35,58010,10÷ 04

54911,6685,37,57010,10÷ 04

5594,6295,37,56010,10÷ 04

овтсещеВ

ecnatsbuS

, × 01

нозапаиД

C°,рутарепмет

erutarepmeT

C°,egnar

кинчотсИ

ecnerefeR

адоВ

retaW

09213,0978,0-5769,094,5-487,17999,00÷ 001]17,94,81[

нирецилГ

lorecylG

07117472466-0105335248-9,13386199,00÷ 05]77,25,3[

ГЭД

GED

813,1-87,068,801-6069,05,734-18,099899,00÷ 051]52[

ГЭП - 004

GEP - 004

00 3,653-3,1644412-2,7838899,052 ÷ 05]24[

ГЭТ

GET

662,1-99,062,511-1,8018,325-1,4117999,04÷ 051]52[

ГЭ

62,6-7,5917,732-8,2414,744-26,760,10÷ 001]48,87,25,3[

2,1 - ДП

2,1 - DP

4,293-86361983-57113802-6,722999,021- ÷ 06]52[

425

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

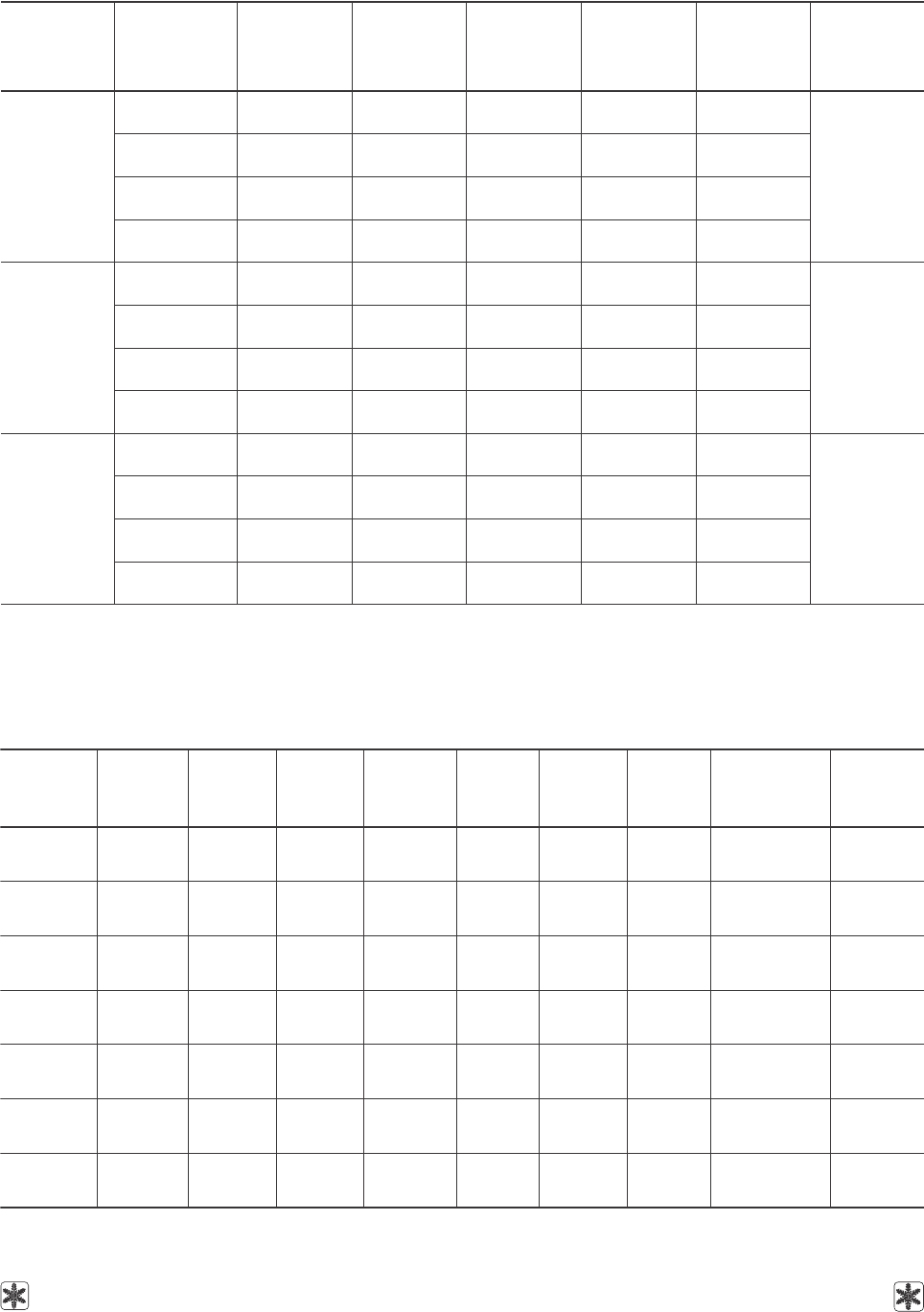
Таблица 5. Коэффициенты уравнения (2) для расчета плотности растворов ряда сахаров в ДМСО в зависимости

от концентрации сахаров при фиксированных температурах; дисперсии аппроксимаций и диапазоны

концентраций применения уравнения

Table 5. Coefficients of equation (2) to calculate the density of some sugars in DMSO depending on sugars’

concentration at fixed temperatures; approximation dispersion and concentration ranges of equation application

Таблица 6. Коэффициенты уравнения (3) для расчета кинематической вязкости воды

и ряда чистых криопротекторов в зависимости от температуры; дисперсии

аппроксимаций и диапазоны температур применения уравнения

Table 6. Coefficients of equation (3) to calculate the kinematic viscosity of water and some pure cryoprotective agents

depending on temperature; approximation dispersion and concentration ranges of equation application

ровтсаР

noituloS

,яицартнецноK

%.ссам

%,noitartnecnoC

)w/w(

, × 01

нозапаиД

C°,рутарепмет

erutarepmeT

C°,egnar

кинчотсИ

ecnerefeR

lCaN

9,2972,1-773,3163,3-565,17999,002 ÷ 001

]94[

8,582,1-293,3393,3-795,17999,002 ÷ 001

7,8203,1-154,364,3-46,17999,002 ÷ 001

6,11433,1-45,3655,3-396,17999,002 ÷ 001

5,41973,1-66,386,3-657,17999,002 ÷ 001

4,71434,1-808,3138,3-928,17999,002 ÷ 001

3,02405,1-199,3210,4-319,17999,002 ÷ 001

2,32865,1-171,4402,4-500,27999,002 ÷ 001

1,6276,1-924,4744,4-11,27999,002 ÷ 001

92277,1-296,4407,4-422,27999,002 ÷ 001

9,13248,1-209,4939,4-143,27999,002 ÷ 001

8,43299,1-172,5472,5-974,27999,002 ÷ 001

арегниР -

аккоЛ

regniR - kcoL

-352,5-978,8846,5-488,12899,05÷ 04]5[

426

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

Таблица 7. Коэффициенты уравнения (3) для расчета кинематической вязкости водных растворов NaCl при

заданной концентрации и раствора Рингера-Локка в зависимости от температуры; дисперсии аппроксимаций и

диапазоны температур применения уравнения

Table 7. Coefficients of equation (3) to calculate the kinematic viscosity of NaCl aqueous solutions

at given concentration and Ringer-Lock solution depending on temperature; approximation

dispersion and temperature ranges of equation application

где коэффициенты d

÷d

имеют размерность сСт

и представлены в табл. 8.

В связи с тем, что для ряда криопротекторов

и их растворов имеется недостаточно экспери-

ментальных данных для построения эмпири-

ческих формул, мы приводим конкретные значе-

ния кинематической вязкости некоторых веществ

и их водных растворов (табл. 9).

Наряду с приведенными выше данными по

плотности и кинематической вязкости для моде-

лирования, например процессов криоконсерви-

рования мелкодисперсных систем, необходимо

учитывать поверхностное натяжение внеклеточ-

ных сред. Поэтому нами были обработаны лите-

ратурные данные по поверхностному натяжению

воды, чистых криопротекторов и их водных раст-

воров.

Поверхностное натяжение σ имеет размер-

ность дин/см (1 дин/см = 10

–3

Н/м).

Для воды и чистых криопротекторов зависи-

мость поверхностного натяжения от температуры

определяется полиномом:

Kinematic viscosity of aqueous solutions of cryo-

protective agents depending on their mass concentra-

tion is described with polynomial equation:

ν = d

+ d

C + d

, (4)

where d

÷d

coefficients have cSt dimension and are

presented in Table 8.

Due to the fact that for some cryoprotective agents

and their solutions there are insufficient experimental

data for derivation of empirical equations we present

the certain values of kinematic viscosity of some sub-

stances and their aqueous solutions (Table 9).

In addition to the presented above data for density

and kinematic viscosity to simulate, for example the

cryopreservation of finely divided systems, it is neces-

sary to consider the surface tension of extracellular

media. Therefore the literature data about surface ten-

sion of water, pure cryoprotective agents and their

aqueous solutions were processed also.

The surface tension σ has a dyne/cm dimension

(1 dyne/cm = 10

–3

n/m).

ровтсаР

noituloS

,арутарепмеТ

C°

,erutarepmeT

C°

, × 01

нозапаиД

йицартнецнок

%.ссам,С

noitartnecnoC

)w/w(%,egnar

кинчотсИ

ecnerefeR

sremylopelbulosretaWыремилопеымировтсародоВ

ГЭП - 0004

GEP - 0004

520255,163,6-760,2324,1-398,05999,00÷ 54]55[

ГЭП - 0006

GEP - 0006

520633,81,03-738,652,51-398,00,10÷ 54]55[

slohoclAытрипС

ГЭ

02-003,4220,03-0821371-0,153 ÷ 05

]3[

51-00872,2268,276,38-89,214999,052 ÷ 05

01-00 789,0-142,134,62-475,55899,002 ÷ 05

0 000 8221,0421,4297,17899,00÷ 05

0100 29,0-24,0101,0803,1989,00÷ 52

02 000 8660,0925,1500,12499,00÷ 05

0500931,0950,0-437,17355,04199,00÷ 05

2,1 - ДБ

2,1 - DB

020743,0268,4-792,235,42-400,11899,00÷ 001

]63[

040870,0540,1-6605,0579,3-556,01999,00÷ 001

3,1 - ДБ

3,1 - DB

020247,04,01-748,468,85-400,19699,00÷ 001

]63[

040381,0215,2-991,113,31-556,01699,00÷ 001

4,1 - ДБ

4,1 - DB

020 6141,0-66,3859,1-15,33400,11499,00÷ 001

]63[

04080,0157,0-8382,0753,0-556,09999,00÷ 001

setardyhobraCыдовелгУ

азорахаС

esorcuS

02640,7400,8-18,23973,5-50,23500,18999,00÷ 06

]18,64,14[

03761,1360,1-218,3684,0-250,4108,00,10÷ 05

427

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

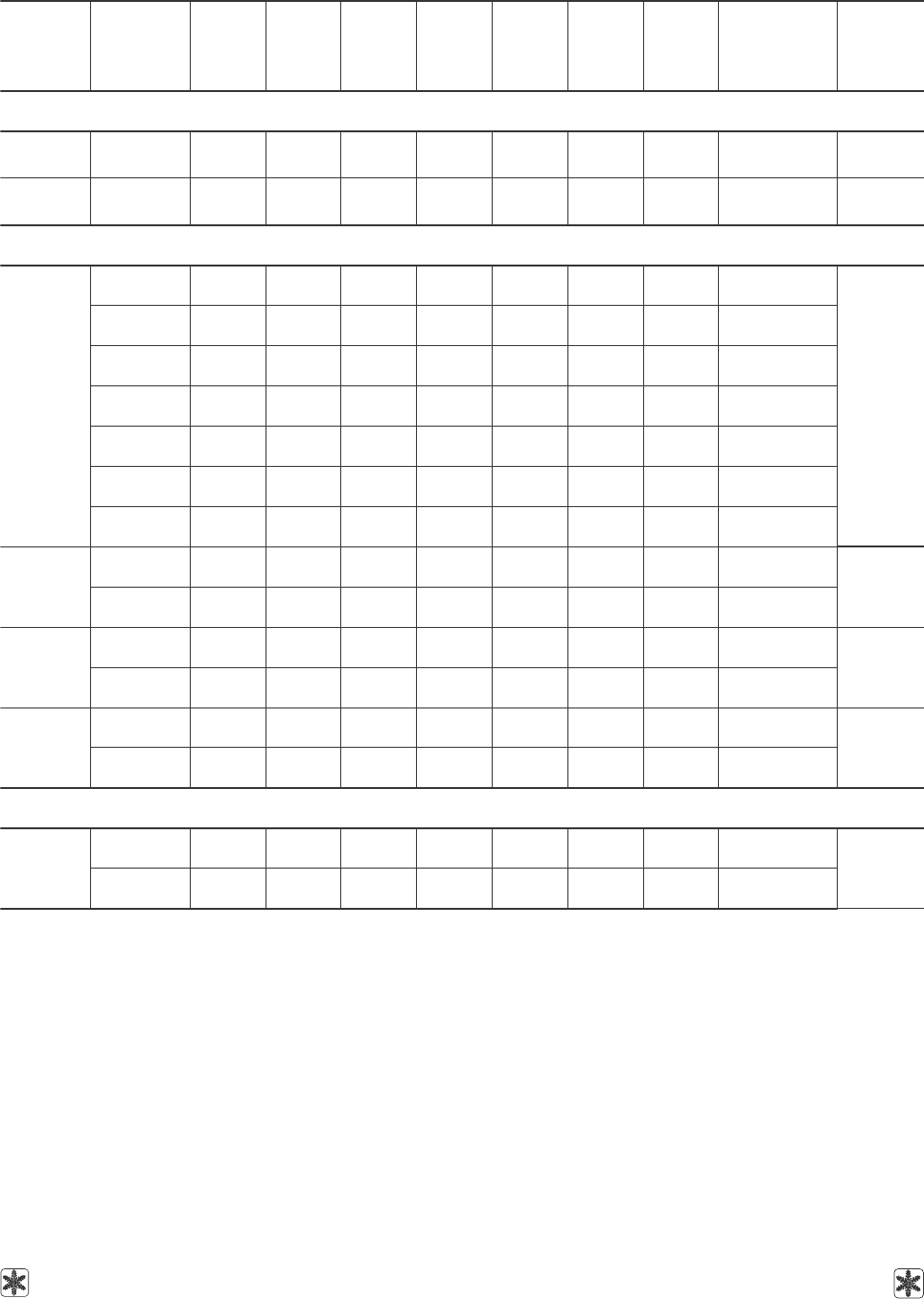
Таблица 8. Коэффициенты уравнения (4) для расчета кинематической вязкости ряда водных растворов

криопротекторов в зависимости от концентрации при фиксированных температурах; дисперсии

аппроксимаций и диапазоны концентраций применения уравнения

Table 8. Coefficients of equation (4) to calculate the kinematic viscosity of some aqueous solutions

of cryoprotective agents depending on concentration at fixed temperatures; approximation

dispersion and concentration ranges of equation application

σ = e

+ e

t + e

. (5)

Значения коэффициентов e

÷e

полинома (5)

для воды и ряда криопротекторов представлены

в табл. 10. Для соблюдения размерности прини-

мается e

– (дин/см)×°С

–4

; e

– (дин/см)°С

–3

;

– (дин/см)°С

–2

; e

– (дин/см)°С

–1

; e

– дин/см.

Подобную зависимость, только описываемую по-

линомом первой степени, имеют водные раст-

воры глицерина, концентрация которых задана в

объемных %. Значения коэффициентов e

и e

представлены в табл. 11.

The dependence of surface tension on tempera-

ture for water and pure cryoprotective agents is deter-

mined with polynomial expression:

σ = e

+ e

t + e

. (5)

Coefficients e

÷e

for polynomial (5) for water and

some cryoprotectants are presented in Table 10. For

keeping the dimension we assumed: e

– (dyn/cm)×°С

–4

;

– (dyn/cm)°С

–3

; e

– (dyn/cm)°С

–2

; e

– (dyn/cm)°С

–1

;

– dyn/cm. The similar dependence described only

with a polynomial of the first degree is characteristc to

овтсещеВ

ecnatsbuS

%.ссам,яицартнецноK

)w/w(%,noitartnecnoC

С°,арутарепмеТ

C°,erutarepmeT

яаксечитамениK

тСс,ьтсокзяв

itameniKc tSc,ytisocsiv

кинчотсИ

ecnerefeR

ГЭД

GED

0011,1223]87[

ГЭТ

GET

0011,1204]87[

нирецилГ

lorecylG

050292,5]87[

лонатЭ

lonahtE

080252,1]04[

lCaN526,514,2]87[

lCaC

53,81651,1]87[

lCaC

526,510,4]87[

овтсещеВ

ecnatsbuS

, × 01

нозапаиД

C°,рутарепмет

erutarepmeT

C°,egnar

кинчотсИ

ecnerefeR

адоВ

retaW

753,3844,7-5810,27841,0-386,571999,004- ÷ 031

,23,22,81,31,7,4[

]26,05

нирецилГ

lorecylG

00 49,733724,0-15,966817,051 ÷ 06

,97,25,84,12,01[

]58

лонатеМ

lonahteM

000 2380,0-272,426199,00÷ 06

,25,51,31,01,6[

]58,97,26

лонапорП

lonaporP

000 3870,0-603,527999,002 ÷ 09]51,31[

ГЭТ

GET

000 880,0-33,74999,002 ÷ 051]28[

ГЭ

00 131-5374,048,345467,051 ÷ 03

,48,08,97,15[

]58

лонатЭ

lonahtE

000 7190,0-231,428979,00÷ 06]97,96,25,01,6[

428

problems

of cryobiology

Vol. 20, 2010, №4

проблемы

криобиологии

Т. 20, 2010, №4

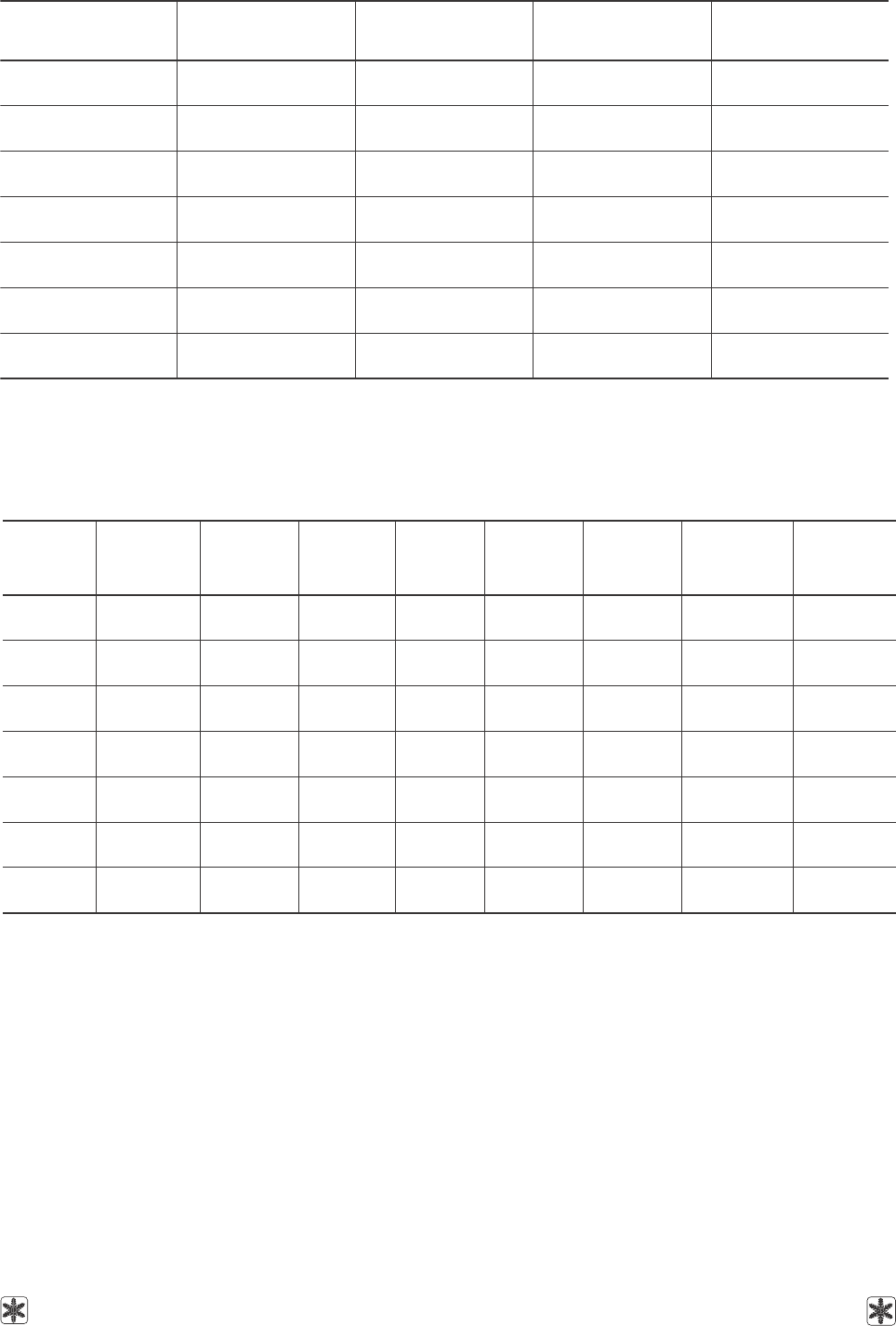
Таблица 9. Кинематическая вязкость некоторых веществ и их растворов

Table 9. Kinematic viscosity of some substances and their solutions

Таблица 10. Коэффициенты уравнения (5) для расчета поверхностного натяжения воды и ряда

чистых криопротекторов в зависимости от температуры; дисперсии аппроксимаций

и диапазоны температур применения уравнения

Table 10. Coefficients of equation (5) to calculate the surface tension of water and some pure cryoprotective agents

depending on temperature; approximation dispersion and temperature ranges of equation application

Для определения поверхностного натяжения

водных растворов криопротекторов в зависимос-

ти от их массовой концентрации используется по-

линомиальное уравнение:

σ = f

+ f

C + f

, (6)

где коэффициенты f

÷f

имеют размерность

дин/см и представлены в табл. 12.

Дополнительно к расчетным данным приво-

дятся средние значения поверхностного натяже-

ния различных криопротекторов и их растворов

(табл. 13).

aqueous solutions of glycerol, which concentration is

gven in % (vol/vol). Table 11 represents e

and e

values.

To determine the surface tension of aqueous solu-

tions of cryoprotective agents depending on their mass

concentration the polynomial equation is used:

σ = f

+ f

C + f

, (6)

where f

÷f

coefficients have dyne/cm dimension and

are presented in the Table 12.

Additionally to the calculated data the average val-

ues of surface tension for different cryoprotective

agents and their solutions are given (Table 13).