Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств

Подождите немного. Документ загружается.

Для косинус-квадратного распределения, имеющего раз-

рывную вторую производную, уровень боковых лепестков

уменьшается как и~

Представляют значительный практический интерес

так называемые оптимальные антенны, распреде-

ление поля в которых таково, что оно обеспечивает за-

данную ширину ДН при минимально возможном уровне

боковых лепестков или же заданный уровень боковых

лепестков при минимально возможной ширине ДН. Для

антенн, состоящих из дискретных излучателей, этот во-

прос рассмотрен в гл. 5. Ниже приводятся результаты

по расчету оптимальных по величине боковых лепестков

линейных антенн с непрерывным распределением тока.

Эти результаты могут быть непосредственно использова-

ны и для антенн с плоским прямоугольным раскрывом,

имеющим независимое по осям распределение поля вида

(2-61).

Выражение для оптимальной по |бок ДН линейной

антенны с непрерывным распределением тока имеет сле-

дующий вид [Л. 1]:

(8)

= cos

тг

}/u

=Af

(2 -65)

где

L .

L — размер раскрыва;

М — параметр, связанный с уровнем боковых лепест-

ков £бок соотношением

сптгМ = т^-. (2-66)

Такая ДН имеет все боковые лепестки одинакового уров-

ня.

Ширина основного лепестка ДН на уровне 0,5 по

мощности однозначно связана с уровнем боковых лепест-

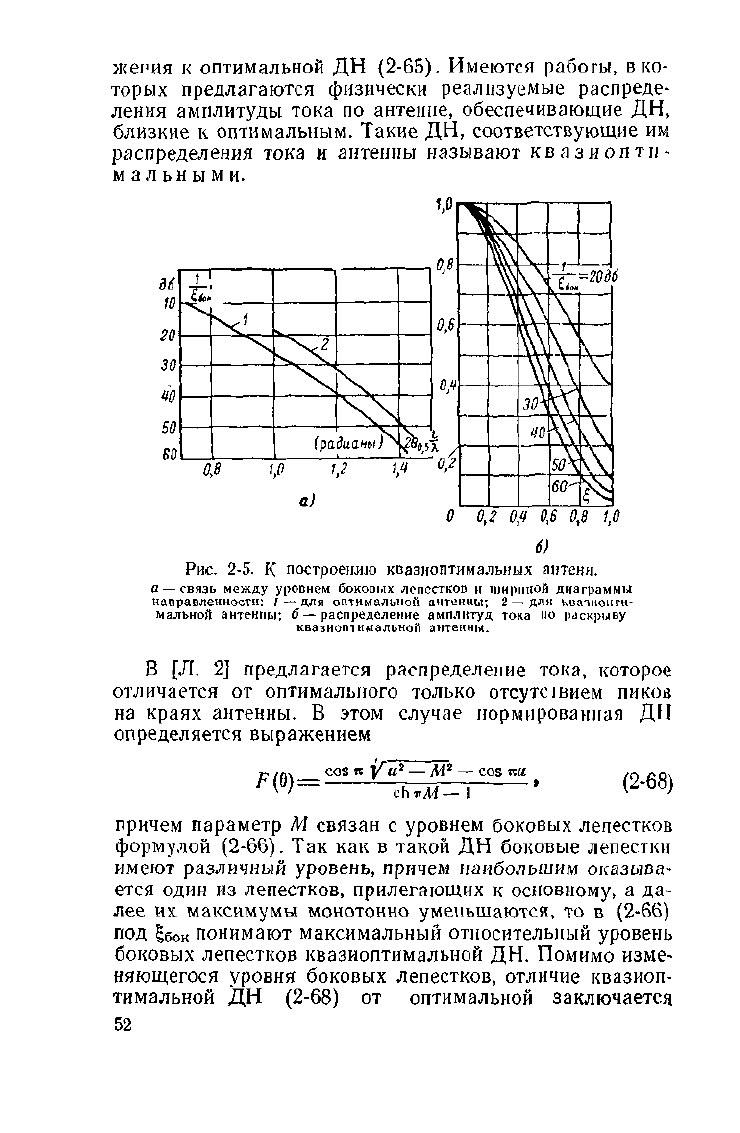
ков (рис. 2-5,а):

20,..

= г l/

arch2

E7-

arch2

^i-'

)

К сожалению, физически реализовать оптимальную ДН

невозможно, так как требуемое распределение тока по

антенне имеет на ее концах бесконечные пики. Поэтому

на практике можно достичь только некоторого прибли-

жения

оптимальной

ДН

(2-65). Имеются работы,

ко-

торых предлагаются физически реализуемые распреде-

ления амплитуды тока

по

антенне, обеспечивающие

ДН,

близкие

оптимальным. Такие ДН, соответствующие

им

распределения тока

антенны называют квазиопти-

мальными.

1.0

ВО

во

Nr'

>ч

ч5

(радианы)^-

=годб

1,0 1,2 1,4

а)

0,2

О 0,2 0,4 0,6 0,8 1,0

Рис.

2-5. К построению квазиоптимальных антенн.

а — связь между уровнем боковых лепестков

шириной диаграммы

направленности:

—

для

оптимальной антенны; 2—дли квазиоиги-

мальной антенны; б—распределение амплитуд тока

по

раскрыву

квазиошимальной антенны.

[Л. 2]

предлагается распределение тока, которое

отличается

от

оптимального только отсутс1вием пиков

на краях антенны.

этом случае нормированная

ДН

определяется выражением

Р(б):

cos

те у и

— М

—

cos

па

chvM—1

(2-68)

причем параметр

связан

уровнем боковых лепестков

формулой (2-66).

Так как в

такой

ДН

боковые лепестки

имеют различный уровень, причем наибольшим оказыва-

ется один

из

лепестков, прилегающих

основному,

а да-

лее

их

максимумы монотонно уменьшаются,

то в

(2-66)

под |бок понимают максимальный относительный уровень

боковых лепестков квазиоптимальной ДН. Помимо изме-

няющегося уровня боковых лепестков, отличие квазиоп-

тимальной

ДН

(2-68)

от

оптимальной заключается

в некотором расширении основного лепестка.

Так же

как

для оптимальной ДН, ширина основного лепестка

при заданной относительной длине антенны связана

с максимальным уровнем боковых лепестков (рис. 2-5,а).

Квазиоптимальной

ДН

(2-68) соответствует следую-

щее распределение тока вдоль антенны, расположенной

по оси:

f(-i-)=

; г-

(ch ir [77W

—

£r

— cos пи)

Xcos(Tiu~)du.

(2-69)

Так

как

интеграл, входящий

(2-69),

общем виде

не

берется,

то

для определения распределения тока

по ан-

тенне используют приближенные методы. Вычисления,

проведенные

в [Л. 2] для

различных значений £бок

(рис.

2-5,6), показали,

что для

понижения бокового

из-

лучения приходится жертвовать величиной КИП.

Другой метод построения квазиоптимальной

ДН

предложен

работе Тейлора

[Л.

3], поэтому соответст-

вующие распределения иногда называют распределения-

ми Тейлора. Квазиоптимальные ДН этого типа характе-

ризуются тем,

что

постоянный уровень боковых лепесг-

1\ов сохраняется

ограниченном секторе углов б вблизи

основного лепестка.

За

пределами этого сектора макси-

мумы боковых лепестков постепенно уменьшаются.

Об-

ласть,

которой боковые лепестки однородны, опреде-

ляются условием

w>M

ysin6, т

= \,2,

. . .

(2-70)

ДН этого типа определяется выражением

т—\

{

—

^М*

(п

—

0,5)

F(«)=ch,Af

i^=L__

;

71)

П[-5]

П-1

При

рассмотрении

ДН

(2-71) масштаб

по оси §

выбран

та-

ким, чтобы размер раскрыва был равен

я.

здесь параметр Y связан с т и М соотношением

1/М

+ (м —0,5)

2 v ;

Рассматриваемые ДН отличаются от оптимальных, кро-

ме особенностей, связанных с боковыми лепестками, и

несколько более широким основным лепестком. Расши-

рение происходит почти точно в у раз, поэтому у назы-

вают коэффициентом расширения ДН:

20...

- 72С- (2-73)

Необходимое для получения ДН типа (2-71) распределе-

ние тока по антенне может быть вычислено по формуле

т—\

f(?f)=F

(0,

m,M) + J*F (п, т, М) cos

-£\,

(2-74)

п=1

где F(n, т, М) определяется выражением (2-71).

Для того чтобы произвести расчет квазиоптимальной

антенны и ее ДН, надо выбрать число т, т. е. установить

границу области однородных боковых лепестков. Чем

больше т, тем ближе ДН к оптимальной, однако значи-

тельно увеличивать т нецелесообразно, так как ширина

основного лепестка при этом уменьшается незначитель-

но.

Для

|бок

= 0'05 значение т должно быть больше трех,

а для

0,01

— больше шести. Основные данные ква-

зиоптимальных ДН этого вида приведены в табл. 2-2.

Таблица 2-2

^бок

дб

м*

0,00000

0,14067

0,33504

0,58950

0,90777

1,29177

1,74229

2,25976

2,84428

0,5

град

28,65

34,49

40,33

45,93

51,17

56,04

60,55

64,78

68,76

Коэффициент расширения ДН f

для разных т

т=2

1,333

1,293

1,244

1,187

1,125

т=3

1,200

1,187

1,159

1,147

1,121

1,092

т=4

1,143

1,136

1,127

1,116

1,103

1,087

1,069

т=5

1,111

1,107

1,102

1,095

1,087

1,077

1,066

1,054

т=6

1,091

1,088

1,085

1,080

1,075

1,068

1,061

1,052

1,043

т=7

1,077

1,075

1,073

1,069

1,065

1,061

1,055

1,049

1,042

т=8

1,067

1,065

1,063

1,061

1,058

1,054

1,050

1,046

1,041

Распределения Тейлора, как правило, имеют всплески

тока на краях антенны, и их реализация оказывается

затруднительной. Поэтому обычно стараются использо-

вать непрерывные системы, имеющие ДН со спадающим

уровнем бокового излучения, которые создаются распре-

делениями без всплесков на краях антенны.

Удобна для реализации ДН вида

slnfrW-M')

75)

где параметр М связан с максимальным уровнем пер-

вого бокового лепестка соотношением

—п~=тг

те

-н—• (2-76)

Этот параметр может быть определен также по задан-

ной ширине основного лепестка ДН из трансцендентного

уравнения

П7П7'Л^-—

(

Кд5

Л<,)

. (2-77)

где

"•..=х

пв

».«-

Амплитудное распределение, соответствующее ДН (2-75),

имеет вид:

/И

(**Л*]Л -

);

(2-78)

здесь /о — функция Бесселя нулевого порядка от мни-

мого аргумента.

Данные ДН вида (2-75) приведены в табл. 2-3. Вид-

но,

что такие ДН уступают рассмотренным выше квази-

оптимальным ДН, но все же достаточно близки к опти-

мальным, причем КИП антенн с ДН вида (2-75) оказы-

вается довольно высоким. Из (2-75) следует, что боко-

вые лепестки с увеличением и уменьшаются как и-

, т. е.

как и у антенн с равномерным распределением. Отличие

от последнего случая

заключавICH

в возможности выбо-

ра уровня первого бокового лепестка.

Таблица 2-3

Об

0,0000

0,1266

0,5455

1,0464

1,6286

2,2011

3,0328

ОПТ J-

0,5 \

град

50,9

52,9

58,7

63,9

68,8

73,2

77,4

1,153

1,151

1,146

1,141

1,136

1,131

1,125

1,000

0,993

0,933

0,863

0,801

0,751

0,709

Получаемые на практике функции распределения по-

ля в раскрыве бывают обычно такими, что определение

ДН оказывается весьма сложной задачей. Для облегче-

ния расчета прибегают к аппроксимации получаемых

функций распределений с помощью более простых функ-

ций, приведенных в табл. 2-1, или их комбинаций. В по-

следнем случае результирующая ДН гюлучае1ся nyieM

простого сложения двух функций, определяющих ДН.

Так, например, для распределения, представляющею

собой сумму постоянного и косинус-квадратного распре-

деления:

/'(*) =

cos

*f.

(2-79)

ДН определяется следующим выражением:

г,, . „sintt , sin и я

Г (и) —С

Г"ТГГ~

~Гг 2V-

(2-80)

Следует иметь в виду, что боковые лепестки, ширина ДН

и другие характеристики ее должны определяться уже

из выражения (2-80), а не с помощью

табл.2-1.

Инте-

ресно, что некоторые типы суммарных распределений

имеют лучшие характеристики, чем характеристики ДН,

определяемой отдельными слагаемыми. Так, для распре-

деления (2-79) при

0,071

максимальный уровень бо-

ковых лепестков равен 43 дб, т. е. значительно ниже,

чем для равномерного и косинус-квадратного распреде-

лений. Ширина же ДН па уровне половинной мощноеiи

равна 76,5 X/L, т. е. тоже лучше, чем у косинус-квадрат-

ного распределения поля,

Приведем критерий, с помощью которого подбирается

аппроксимирующая функция. Если функция распределе-

ния симметрична относительно центра раскрыва, что

обычно выполняется на практике, то ДН может быть

представлена в виде

F(U):

_РоА_

(1-рг

2цо

(2-81)

где ц,

—

момент, характеризующий распределения поля в

раскрыве, определяемый как

—1

(2-82)

—

постоянный коэффициент.

Так как ц

убывает с увеличением т, то в пределах

главного и первых боковых лепестков ДН в основном

определяется первыми членами ряда (2-81). Отсюда сле-

дует, что для того, чтобы

аппроксимирующая функ-

ция обеспечивала хорошее

приближение к истинной

ДН антенны, квадратич-

ный момент ее площади

относительно центральной

оси должен быть равен

квадратичному моменту

площади реальной функ-

ции распределения. Так

как кривая истинного рас-

пределения поля в рас-

крыве обычно задана в

виде графика, то аппро-

ксимацию наиболее удоб-

но проводить графиче-

ским путем. Следует

иметь в виду, что особен-

ностью данного метода аппроксимации является измене-

ние величины скачка Л на краю раскрыва.

Круглый раскрыв. На практике часто встречаются ан-

тенны, имеющие круглый раскрыв (рис. 2-6). Так, на-

пример, зеркальные и линзовые антенны, создающие

игольчатые ДН, имеют обычно круглые раркрывы. Век-

Рис.

2-G К расчету напряженности

поля, создаваемого плоским син-

фазным круглым раскрывоч

в дальней зоне.

торная функция

(2-56), определяющая ДИ,

случае

плоского круглого раскрыва

линейной поляризации,

параллельной плоскости xoz, имеет вид:

{

[ExirW'le'^'^^^^'Vdr'df,

(2-83)

где

б,

ф —

угловые координаты точки наблюдения;

r'q/

—

координаты точек раскрыва;

D=2R

—

диаметр раскрыва.

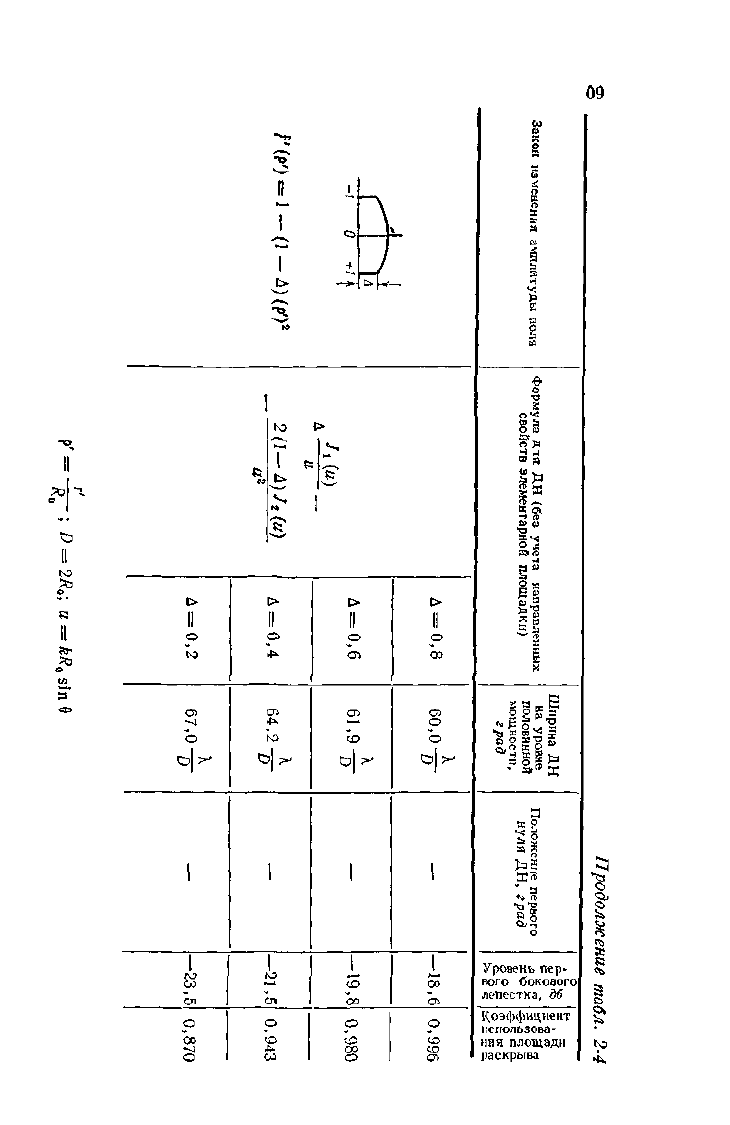
ДН плоских синфазных круглых раскрывов при раз-

личных распределениях амплитуды поля даны

в табл. 2-4.

Интересно распределение, равномерное

по

окружно-

сти,

т. е.

не зависящее от угла q/,

спадающее

краям

по закону

/'(p')

(l-A)cos

^, (2-84)

где

Р=ТГ-

Функция (2-84) очень хорошо описывает распределение

поля

зеркальных антеннах

зеркалом

виде парабо-

лоида вращения, особенно при равномерном облучении

его

азимутальной плоскости.

ДН круглого синфазного раскрыва

указанным рас-

пределением поля определяется следующим выраже-

нием:

F(u)

= b^ + (1-A)x

(u),

(2-85)

где и

(и)

— функция, рассчитываемая

помощью соотно-

шения

и.

(и)

= j

Р'Л (ир')

cos

dp', (2-86)

£/?„

sin б.

Приводимые ниже формулы для круглого раскрыва получены

А. С. Лавровым.

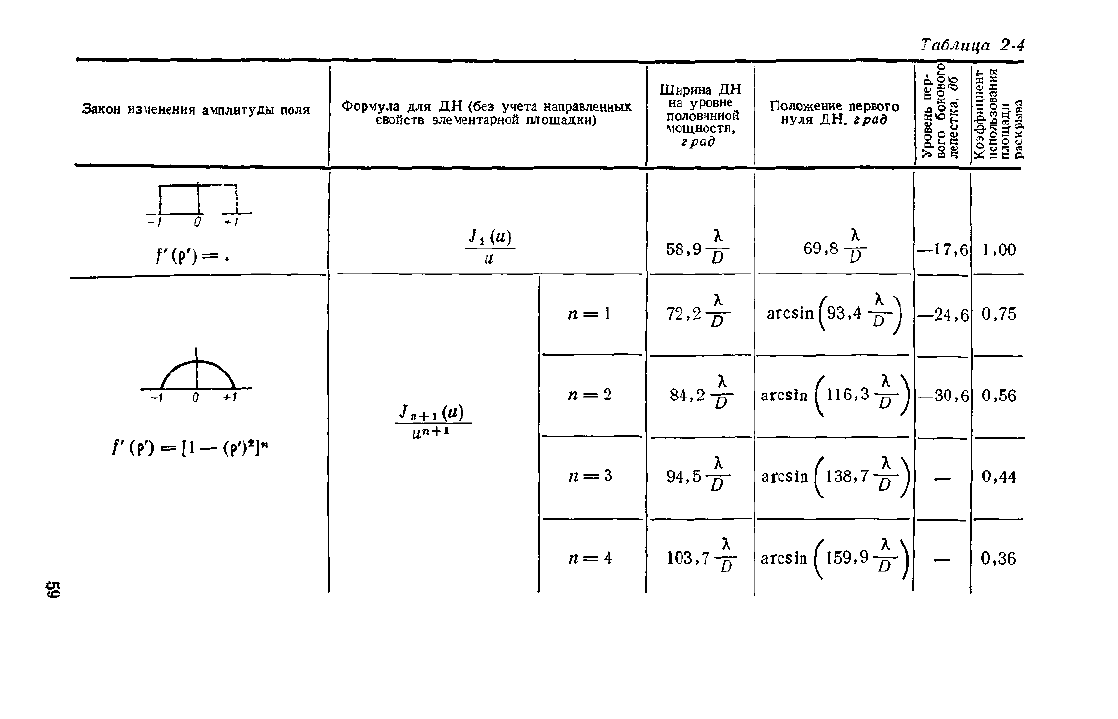
Таблица 2-4

Закон изменения амплитуды поля

Г(Р')=-

к_

-1 0 +1

/'(p') = [i-(p'№

Формула для ДН (без учета направленных

свойств элементарной площадки)

1,(4)

Jn+i(u)

цП+1

= \

п = 2

и = 3

п = 4

Ширина ДН

на уровне

половинной

ЛЮЩНОСТИ,

град

58,9-д-

72,2 ^

84,2^

94,5-^

103,7-р-

Положение первого

нуля ДН, град

69,8 -у-

arcsinf 93,4-ту-

arcsin ( 116,3 -ту- 1

arcsin ( 138,7-ту- 1

arcsin f 159,9-^-J

i°»

к _-

л о S

«о

£g§

— 17,6

—24,6

—30,6

—

Коэффициент

использования

площади

раскрыва

1,00

0,75

0,56

0,44

0,36

из

о]

СС

оо

•а

о^

а й

л Я

«г

•а

я^

гя,Е

Ja3

Уровень

пер-

вого бокового

лепестка,

дб

СО

Коэффициент

использова-

ния

площади

раскрыва