Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств

Подождите немного. Документ загружается.

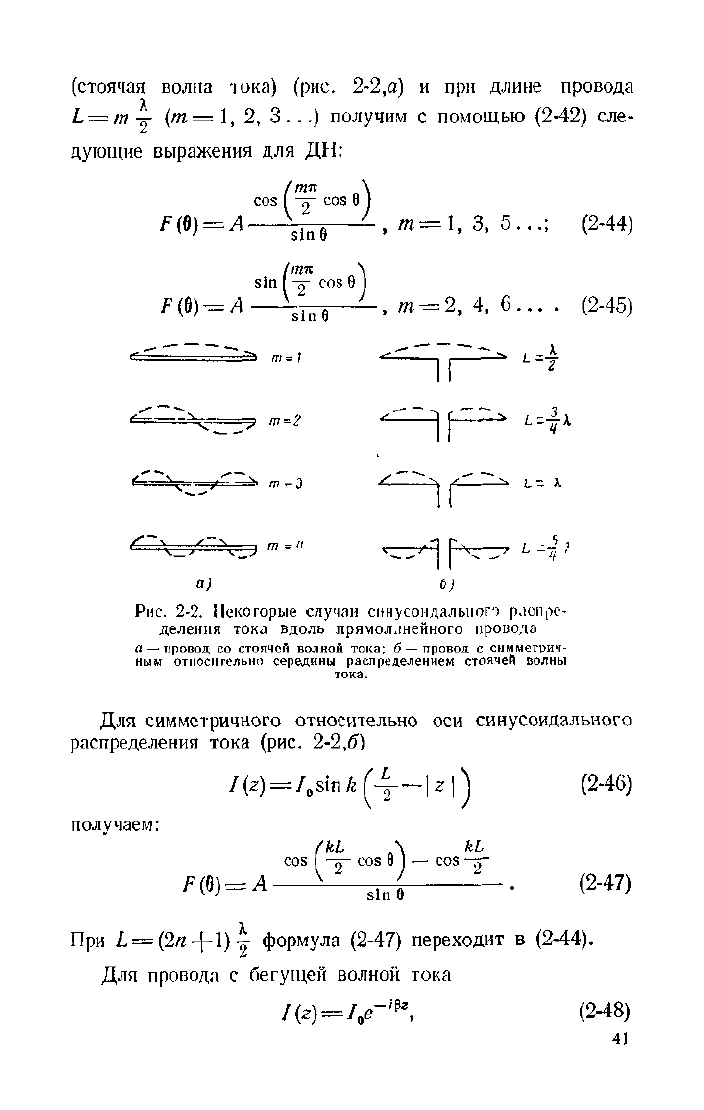
(стоячая волна тока) (рис. 2-2,а) и при длине провода

= т

-п-

(т=1, 2, 3. ..) получим с помощью (2-42) сле-

дующие выражения для ДН:

cos

-s" cos

$) =

A-

We -,«=1,3,5...; (2-44)

Inm \

sin

-„- cos

b)^A—\

-^-, ni = 2, 4, 6... . (2-45)

=s>

^_^^i^

=? m = 2

*- -j

[—

* t^fA

^ m

3 ^— 1=, f" ~~-> Lt A.

1Г

f"~\ /~X

" < +3, P-\ , i, ^4

a) 6)

Рис.

2-2. Некоторые случаи синусоидального распре-

деления тока вдоль прячоллнейного провода

—-

провод со стоячей волной тока; б — провод с симметрич-

ным относительно середины распределением стоячей волны

тока.

Для симметричного относительно оси синусоидального

распределения тока (рис. 2-2,6)

/(z)

= /

sin/«(4-|

(246

получаем:

'kL \ kL

cos I -р- cos

I — cos -х-

F(9) = A ^ ^ • (2-47)

При

= (2«4-l)-2 формула (2-47) переходит в (2-44).

Для провода с бегущей волной тока

/(г) = 1

е-

, (2-48)

где

ю/и,

a v

—

фазовая скорость волны вдоль провода,

получается следующая формула для ДН:

sin

F(i) = A

f „

-~- cos

—

(co.0—J-)

•sin 6.

(2-49)

В формулах (2-44), (2-46), (2-47) и (2-49)

—норми-

рующий множитель.

2-3.

РАСЧЕТ ДИАГРАММ НАПРАВЛЕННОСТИ АНТЕНН

С ИЗЛУЧАЮЩИМ РАСКРЫВОМ

Большое количество антенн, особенно на сверхвысо-

ких частотах, имеет излучающий раскрыв, т. е. поверх-

ность, через которую происходит излучение. Такой рас-

крыв представляет собой не-

которое отверстие (аперту-

ру) в проводящей поверхно-

сти,

на которой первичные

источники возбуждают высо-

кочастотные токи. Так как

•проводящая поверхность,

как правило, имеет весь-

ма сложную форму, то

метод определения поля из-

лучения по токам, которые

к тому же еще нужно найти

на проводящей поверхности,

оказывается малопригодным.

Для расчета антенн с из-

лучающим раскрывом обыч-

но применяют приближен-

ный метод, который, как

правило, вполне удовлетворяет требованиям практики.

Сущность этого метода заключается в следующем.

Все пространство разбивают на две области. Одна из

областей является внутренней, а вторая

—

внешней

(рис.

2-3). Внутренняя и внешняя области связаны толь-

ко через поверхность раскрыва, так как вся остальная

граничная поверхность между этими областями пред-

ставляет собой проводник. В соответствии с таким раз-

биением пространства решают две задачи

—

внутреннюю

и внешнюю. При решении первой задачи в болынинст-

^ca

Рис.

2-3. К определению напря-

женности поля, создаваемою

излучающим раскрывом в даль-

ней зоне.

—

источник электромагнитного по-

ля;

—>

внутренняя сторона поверх-

ности; 3

—

внешняя сторона поверх-

ности, 4 -~ поверхность раскрыва;

—

внутренняя область (объем);

—

внешняя область (объем).

ве практических случаев используют приближенные ме-

тоды и находят поле в объеме Vi независимо от внеш-

него объема V

. Например, для определения поля в рас-

крыве зеркальных и линзовых антенн используют мето-

ды геометрической оптики. В результате становится из-

вестным распределение поля на поверхности, совпадаю-

щей с поверхностью раскрыва реальной антенны.

Так как поверхность раскрыва является общей для

обеих областей, то, следовательно, известно поле для

части поверхности, ограничивающей внешнюю область.

На остальной поверхности внешней области поле обыч-

но полагают равным нулю и считают, что на ней отсут-

ствуют также токи и заряды. Во многих практических

случаях такие допущения вполне оправданы, особенно

когда интересуются только основным и первыми боко-

выми лепестками ДН, максимум которой ортогонален

поверхности раскрыва. Таким образом, внешняя задача

сводится к нахождению поля во всей внешней области

по известным значениям поля на части поверхности, ог-

раничивающей область. Для решения этой задачи удоб-

но воспользоваться принципом эквивалентности, кото-

рый позволяет использовать для нахождения поля во

внешней области формулы (2-20).

Принцип эквивалентности заключается в том, что

электромагнитное поле в области V, не содержащей

внутри себя источников поля и ограниченной поверхно-

стью S с заданными на ней значениями векторов поля

Е и Н, тождественно совпадает с полем, возбуждаемым

в этой же области поверхностными электрическими и

магнитными токами, распределенными на поверхности

S с поверхностной плотностью, равной соответственно:

К = НХп, К^ — ЕХп. (2-50)

Напомним, что п — единичная нормаль к поверхности

S, внешняя по отношению к объему V.

Как это следует из (2-50), на поверхности S доста-

точно знать только тангенциальные составляющие век-

торов поля Е и Н. Векторы Е и Н в (2-50) являются

векторами некоторого электромагнитного поля и не мо-

гут быть взяты произвольно. Заметим также, что вне

объема V поля токов К и К^ равны нулю.

Зная поле на части поверхности, ограничивающей

внешний объем (раскрыв антенны), и пользуясь принци-

пом эквивалентности, иоле в этом объеме можно

определить по формулам (2-20), которые принимают

вид:

= 4^7 j 1№Хп) VI grad / + V (НХп) / +

+ io.e[(EXn)Xgrad/]}ds;

где

4ягц>е

j{[(EXn)V]grad/ + ft

(EXn)/-

• (2-51)

t«|i[(HXn)xgrad/]}ds,

—ikR>

f=-

R'—

расстояние между точкой интегрирования на 5

и точкой наблюдения.

В общем случае поле в объеме V может создавать-

ся как излучающим раскрывом, так и сторонними то-

ками других источников. Поле в объеме будет представ-

лять собой в этом случае сумму полей, определяемых

формулами (2-17) и (2-51). Формулы (2-51) являются

обобщением скалярных формул Кирхгофа на случай

уравнений Максвелла и являются математическим вы-

ражением принципа Гюйгенса.

Для дальней зоны формулы (2-51) упрощаются:

h n-lkR

№

Л+л

„.К +

|л<р

где

$(ЕХп)е'

kpcos &

ds.

(2-53)

В (2-53) p, как и раньше, — расстояние от начала си-

стемы координат до текущей точки раскрыва. Обычно

предполагают, что векторы поля в раскрыве связаны со-

отношением

=a(H,Xn), (2-54)

где Е

(

и Н

(

— касательные составляющие векторов по-

ля в раскрыве;

—

некоторый постоянный коэффициент, на-

зываемый волновым сопротивлением рас-

крыва.

Этот коэффициент нужно определять в каждом от-

дельном случае, однако для синфазных раскрывов мож-

но считать, что

= j/-£ = 120ir,

т. е. таким, как и для свободного пространства.

При выполнении (2-54) формулы (2-52) для плоско-

го раскрыва упрощаются:

Е =

4га R

где

«х(

-т/т

«)х

(2-55)

N= f Ete'

cos

*ds. (2-56)

Магнитное поле определяется с помощью второго соот-

ношения (2-52).

В случае определения поля остронаправленной ан-

тенны, в плоском раскрыве которой a~|/ju/e, формула

для определения поля вблизи основного лепестка ДН

еще более упрощается:

Е=

^-Х-"

[е

^Хп)],

(2-57)

где N определяется формулой (2-56). Подчеркнем еще

раз,

чго последняя формула справедлива для плоских

синфазных раскрывов с большими размерами по отно-

шению к длине волны, излучающих нормально раскрыву.

Существуют и другие методы определения электро-

магнитного поля, например, методы вспомогательных

источников, стационарной фазы, скалярного интеграла

Кирхгофа. Все они каких-либо существенных пре-

имуществ перед изложенным методом нахождения поля

не имеют.

Однако метод скалярного интеграла Кирхгофа часто

находит применение на практике. Учитывая это, приве-

дем формулу Кирхгофа, позволяющую вычислить значе-

ние скалярной функции и

, удовлетворяющей волновому

уравнению, в точке наблюдения М, если известны зна-

чения самой функции v

и ее производных по нормали

dvs/dn на поверхности S, ограничивающей рассматри-

ваемый объем:

-=Hj(»s£-t£)*•

58)

где

p-lkR

Скалярная функция v

соответствует одной из состав-

ляющих векторов Ей Н, каждая из которых удовлетво-

ряет волновому уравнению.

На практике интегрирование в (2-58) производят

только по поверхности раскрыва антенны, полагая, что

на остальной поверхности, примыкающей к раскрыву,

функция а и ее производная по нормали равны нулю.

Если также считать, что фронт волны в раскрыве бли-

зок к синфазному, а амплитуда поля по раскрыву изме-

няется медленно, то для дальней зоны (2-58) можно

преобразовать к виду

Ум

= % ~^- \ ve

ik рГГ

(s е

+ cos

ds, (2-59)

где р— радиус-вектор точки в плоскости раскрыва

(рис.

2-4);

R° —

единичный вектор, направленный из начала ко-

ординат в точку наблюдения;

s — единичный вектор, ортогональный фронту вол-

ны в раскрыве.

Интегрирование в (2-59) выполняется только по пло-

щади раскрыва. Если фронт волны в раскрыве плоский

(s||e

а ДН достаточно узкая (cos6«d), то (2-59)

упрощается и принимает вид:

™

= 2l-

,—lkR

(vdS. (2-60)

Приведенные выше векторные формулы ненамного

сложнее формулы Кирхгофа, но более правильно отра-

жают картину поля антенны в дальней зоне.

Достаточно подробно метод Кирхгофа, а также дру-

гие методы расчета полей антенн рассмотрены в [ЛО. 30].

2-4. ДИАГРАММЫ НАПРАВЛЕННОСТИ ПЛОСКИХ

СИНФАЗНЫХ РАСКРЫВОВ

Прямоугольный раскрыв. ДН прямоугольного раскры-

ва со сторонами А и В (рис. 2-4), имеющего поле с ли-

нейной поляризацией, обычно определяют в предположе-

нии, что амплитудное рас-

пределение поля по рас-

крыву можно представить

в виде

f'(x,y)=f\(x)f',(y).

(2-61)

В этом случае двойные

интегралы по поверхности

раскрыва в формулах для

определения поля превра-

щаются в произведение

однократных интегралов,

каждый из которых опре-

деляет поле некоторого

линейного источника с распределением

f'i(x)

и /'г(у)-

Если поле в раскрыве линейно поляризовано и плоскость

поляризации параллельна оси ох, то ДН в £-плоскости

будет определяться только распределением

f'i(x),

а в Н-

плоскости

—

Гг(у). так как интеграл, определяющий поле

антенны, например (2-56), принимает вид:

Рис.

2 4. К расчету напряжен.юсти

поля, создаваемого плоским сич-

фазным прямоугольным раскры-

воч в дальней зоне.

А/2

в/2

f J

Е'

(х)

Е"

(у)

—А/2 -В/2

Ik sin 9

(*"cos

<f—u

sin (f)

dxdy.

(2-62)

Отсюда видно, что ДН в ^-плоскости

(ср

= 0) описывается

функцией

+ i

(2-63)

—1

где

+ i

— i

В //-плоскости

(<р

= те/2) ДН соответствуе

выражению

+ i

= e

C'J£"

,(S')e"''*'<#; (2-64)

-i

здесь

+ i

W = ~ sin

C'= f £\(!=)Л.

-l

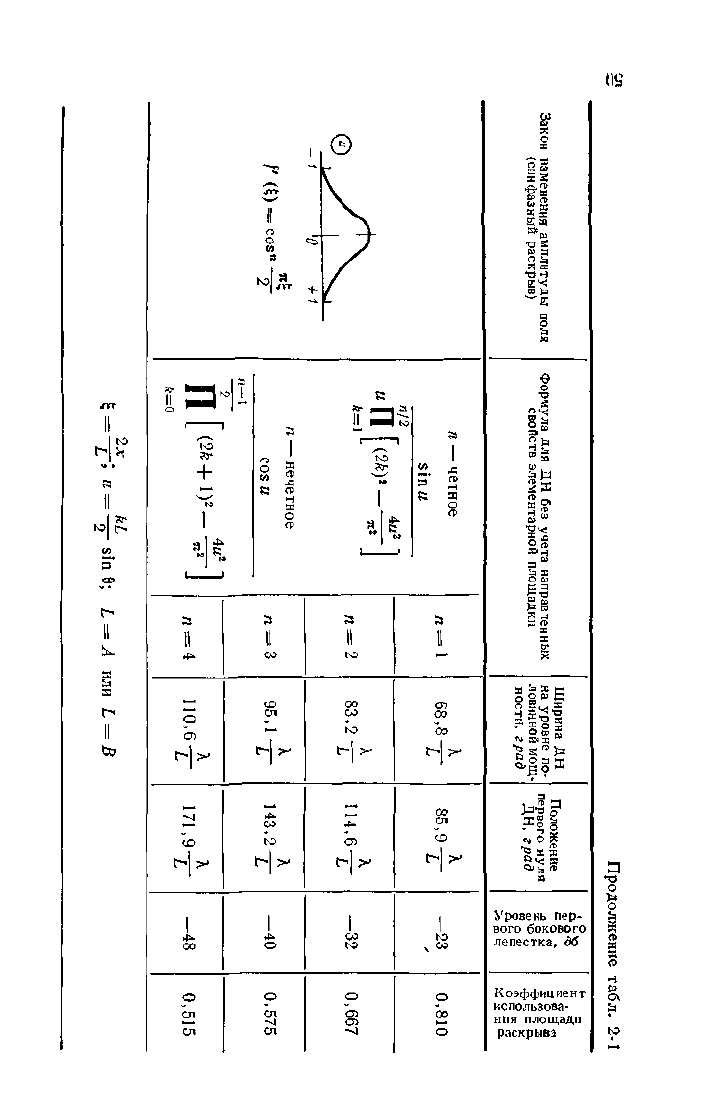
Результаты расчета ДН синфазного плоского рас-

крыва для некоторых функций распределения амплиту-

ды поля приведены в табл. 2-1.

На практике значительное внимание уделяется умень-

шению величины боковых лепестков Как видно из

табл. 2-1, величина первого бокового лепестка зависит

от вида функции распределения амплитуды поля, и она

тем меньше, чем меньше уровень поля на краю раскры-

ва. При этом следует отметить, что величина первого

бокового лепестка зависит и от распределения поля

у края раскрыва, что хорошо видно из сравнения уров-

ня бокового лепестка для распределений

/(A:) = COS™ и /(л) =

соь

Уровень боковых лепестков, соответствующих большим

углам 6 (большее значение и), уменьшается, причем ин-

тенсивность уменьшения зависит опять-таки

о г

вида рас-

пределения. Так, для равномерною распределения, когда

функция распределения и ее первая производная терпят

разрыв на краю раскрыва, уровень боковых лепестков

уменьшается как и

-1

. Для треугольного и косинусоидаль-

ного распределения, которые имеют непрерывные функ-

ции распределения, но первая производная терпит раз-

рыв,

уровень боковых лепестков уменьшается как w

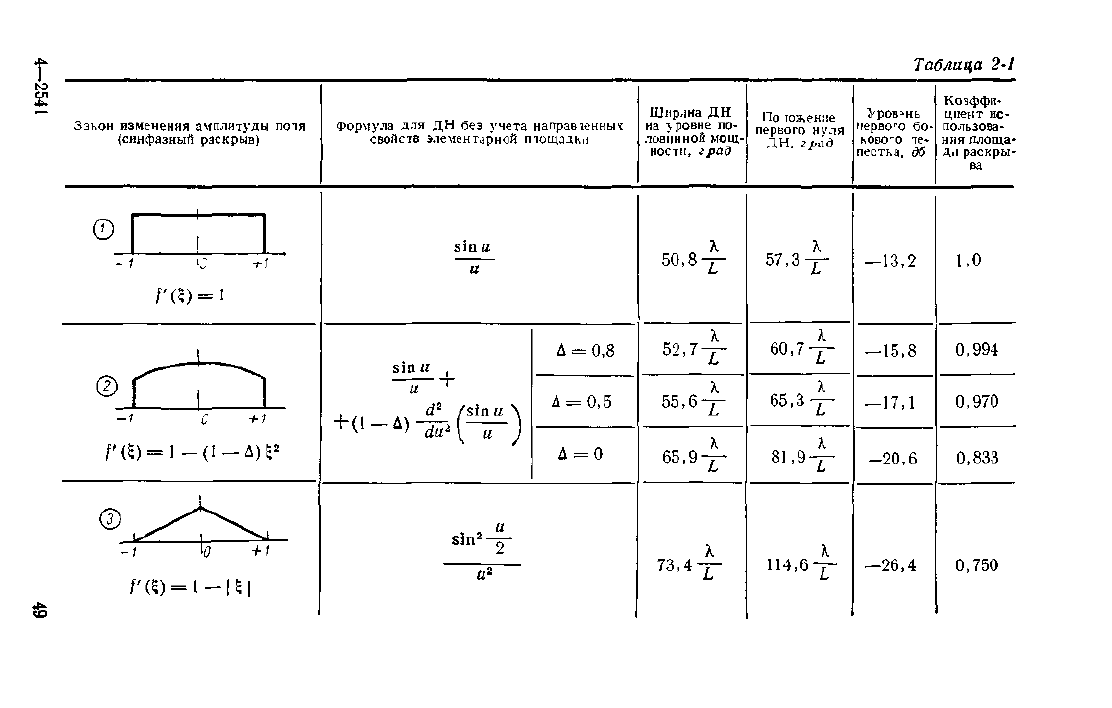
Таблица 2-1

JakOH изменения амплитуды потя

(синфазный раскрыв)

Формула для ДН без учета направченны^

свойств элементарной тощадкп

Ширина ДН

на \ ровне по-

ловинной мощ-

ности, град

По юженпе

первого нуля

ДН, град

\ров^нь

первого бо-

ково"0 те-

пестка, дб

Коэффи-

циент ис-

пользова-

ния площа-

ди раскры-

ва

/'(?)

-1 С +1

<5)

—

А>

sin

, d

/sin и

)-5Р

sin

= 0,5

= 0

50,8-^

т-

55,6-

65,9-

73,4^

57,3-

60,7-

65,3-

81,9-

114,

6т

— 13,2

—15,8

17,1

-20,6

—26,4

1,0

0,994

0,970

0,833

0,750

I tO

so-

. ©

•—n "-*•

JTlf

О CD

H- i-

„

_1.

о • 1

t 1

Кг тщ а

э»

3 -

1 ' - '

ft О)

— i-j

ft-

1 1

к я

(Р

О)

t-]

t-l

>•

ел

СЛ

СО

ел

с-|

t-|

ел

—i

ел

оо

г-| >•

t—J

г-"

со

Сл

ел

-I

СП

со

[

f- р-

со

ел

со

t-l >•

ч "

со

G w

Е а

•о £

•а н

"""" Е

•о

ге

гт.

ffi

_ и

О си

£3

я и

ГО

<М

н« a

и о a •г

- ^ о

Си ^

Уровень

пер-

вого бокового

лепестка,

дб

Коэффициент

использова-

ния

площади

раек

рыв а

•о

)а