Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств
Подождите немного. Документ загружается.


поля Е и Н, то построенные графики показывают изме-
нение в зависимости
о г
углов 8 и у соответствующих
компонент векторов напряженности электрического и маг-
нитного полей в некотором масштабе. Поскольку функции
N
6
\
и \N | являются функциями [двух переменных, то в
пространстве ДН представляет собой [некоторую замкну-
тую поверхнось, радиус-вектор которой равен в некото-
ром
масш 1 абе
величине | N | или
|
N |. В общем случае
Рис.
1-1. Диаграмма направленности
антенны
/ — главный (основной) лепесгок диаграммы
направленности; 2 — боковые (побочные) ле-
пестки диаграммы направленности. 3 — задний
лепесток диаграммы направленности
эта поверхность представляет собой несколько объемных
лепестков различной формы. Наибольший из них называют
главным или основным лепестком ДН, остальные
—
боко-
выми или побочными лепестками (рис. 1-1). Если ДН имеет
лепесток, направление коюрого противоположно основному,
то его называют задним лепестком.
На практике обычно интересуются не пространствен-
ной ДН, а ее сечениями какими-либо характерными
плоскостям,!. В качестве таких плоскостей часто выби-
рают две взаимно перпендикулярные плоскости, линия
пересечения которых совпадает с направлением макси-
мума ДН. Одну из этих плоскостей обычно совмещают
с вектором Е и называют ^-плоскостью. Очевидно, что
в силу ортогональности векторов поля в дальней зоне
другая плоскость будет совпадать с вектором Н и назы-
вается Я-плоскостью. Сечение ДН /^-плоскостью назы-
вают ДН в ^-плоскости, а Я-плоскостыо
—
ДН в Я-пло-
скости.
Легко видеть, что сечение ДН какой-либо плоскостью
будет представлять собой кривую на плоскости, изобра-
11
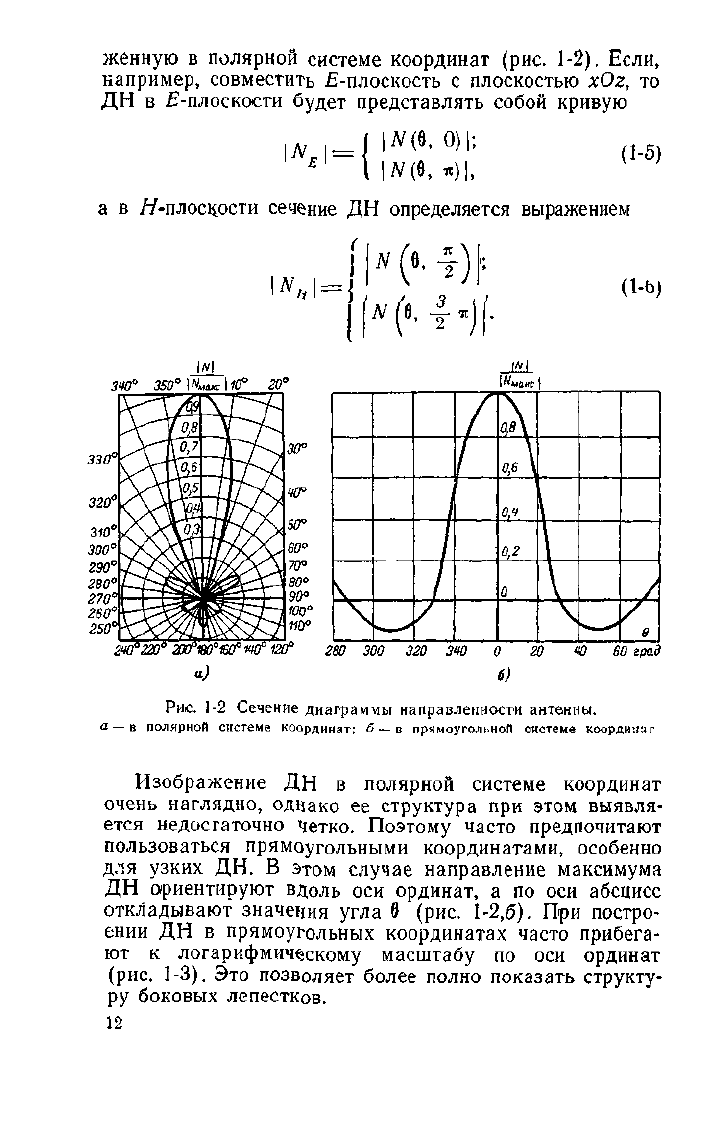
женную
в
полярной системе координат
(рис. 1-2).
Если,
например, совместить ^-плоскость
с
плоскостью
хОг, то
ДН
в
^-плоскости будет представлять собой кривую
1*
£
1
=
iV(6,
0)|;
JV(6,
IT)
|,
а
в
//-плоскости сечение
ДН
определяется выражением
Г
(1-5)
N
Ь
>-т)
"*1=Ч,
/ з
240°220°
200°180°160°
ПГ
а)
280 300 320 340
20
6)
(1-b)
А
0,6 1
0,*
о, г
0
9
«0 60 гра<?
Рис.
1-2 Сечение диаграммы направленности антенны.
в полярной системе координат; б —в прямоугольной системе координат
Изображение ДН в полярной системе координат
очень наглядно, однако ее структура при этом выявля-
ется недосгаточно Четко. Поэтому часто предпочитают
пользоваться прямоугольными координатами, особенно
для узких ДН. В этом случае направление максимума
ДН ориентируют вдоль оси ординат, а по оси абсцисс
откладывают значения угла б (рис.
1-2,6).
При постро-
ении ДН в прямоугольных координатах часто прибега-
ют к логарифмическому масштабу по оси ординат
(рис.
1-3). Это позволяет более полно показать структу-
ру боковых лепестков.
12
В некоторых случаях, например при построении ДН
с учетом влияния земли, удобнее направить ось z вер-
тикально и строить сечения ДН плоскостями
ф
=
<р^
л
,
Ф
,:
=
=
Фгл
+ я и конической поверхностью
8
—6
ГЛ
:
где углы
(рис.
1-4).
\N
B
\ =
I^V(8,
?гл
)|;
>(9
1?1Л
+
«)|;
|^| =
|^(в
гл>
?)|,
^гл и <р
гл
соответствуют максимуму
0-7)
(1-8)
ДН
Itl
'с
/
маис
Л
\
1
_А
А
\
V
г\
\
г
\г
S
в
О
-10
-го
-
-зо -
-ад
О 20 НО SO 80 100 120 ШО
КО
град
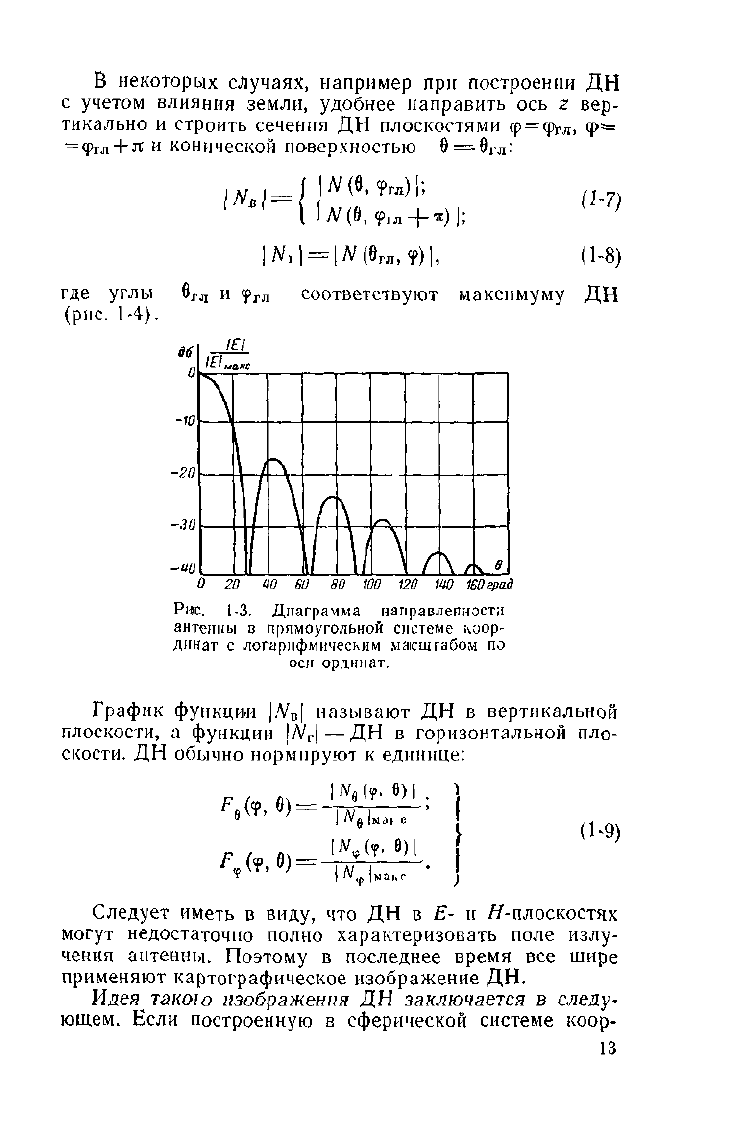
Рис.
1-3. Диаграмма направленности
антенны в прямоугольной системе коор-
динат с логарифмическим масштабом по
оси ординат.
График функции |/V
E
| называют ДН в вертикальной
плоскости, а функции \N
r
\—ДН в горизонтальной пло-
скости. ДН обычно нормируют к единице:
FAvJy-
\N
t
(
v
,
9)| . )
F,(?J)-
I J*Q (МЛ С
IV?-
9
)l
}
(Щ
Следует иметь в виду, что ДН в Е- и Я-плоскостях
могут недостаточно полно характеризовать поле излу-
чения антенны. Поэтому в последнее время все шире
применяют картографическое изображение ДН.
Идея такого г^зображенпя ДН заключается в следу-
ющем. Если построенную в сферической системе коор-
13
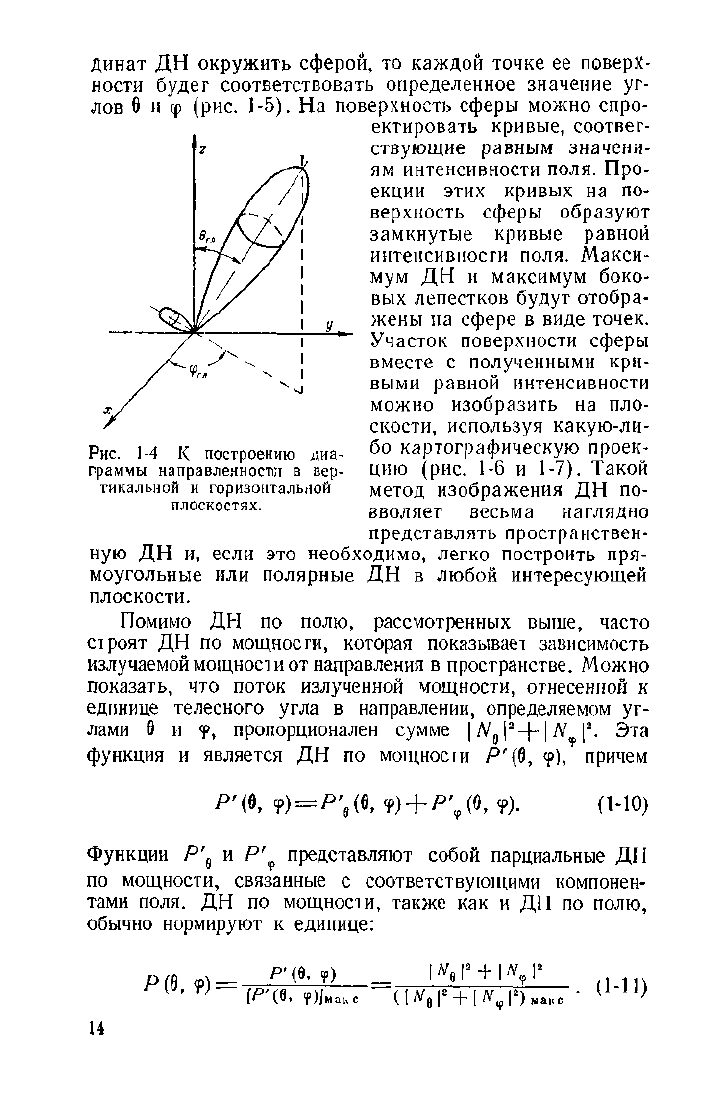
Динат ДН окружить сферой, то каждой точке ее поверх-
ности будет соответствовать определенное значение уг-
лов 6 и ф (рис. 1-5). На поверхность сферы можно спро-
ектировать кривые, соответ-
ствующие равным значени-
ям интенсивности поля. Про-
екции этих кривых на по-
верхность сферы образуют
замкнутые кривые равной
интенсивности поля. Макси-
мум ДН и максимум боко-
вых лепестков будут отобра-
жены па сфере в виде точек.
Участок поверхности сферы
вместе с полученными кри-
выми равной интенсивности
можно изобразить на пло-
скости, используя какую-ли-
бо картографическую проек-
цию (рис. 1-6 и 1-7). Такой
метод изображения ДН по-
зволяет весьма наглядно
представлять пространствен-
ную ДН и, если это необходимо, легко построить пря-
моугольные или полярные ДН в любой интересующей
плоскости.
Помимо ДН по полю, рассмотренных выше, часто
строят ДН по мощности, которая показывает зависимость
излучаемой мощности от направления в пространстве. Можно
показать, что поток излученной мощности, отнесенной к
единице телесного угла в направлении, определяемом уг-
лами 8 и «р» пропорционален сумме
17V
Q
j
2
—|— |
Л''
|
2
. Эта
функция и является ДН по мощное!и Я'(б, <р), причем
Рис.
1-4 К построению диа-
граммы направленности в вер-
тикальной и горизонтальной
плоскостях.
Р'(9,
?) = Р'
9
(6, ?) + Я;(0, ?).
(1-10)
Функции Р'
9
и Р' представляют собой парциальные ДП
по мощности, связанные с соответствующими компонен-
тами поля. ДН по мощности, также как и ДП по полю,
обычно нормируют к единице:
Р(6,
9) =
Р'(в. ?)
ItfJ'
+ IAU"
[/"(в,
?)]«аьо (|Лд
2
+
[^,(,[
2
)ма„с
• (Ml)
14
Построение различных сечений ДН по мощности совер-
шенно аналогично рассмотренным выше построениям
сечений ДН по полю.
Направленные свойства антенны оценивают по вели-
чине угла раствора ДН в какой-либо плоскости на за-
данном уровне напряженности или мощности поля. Ве-
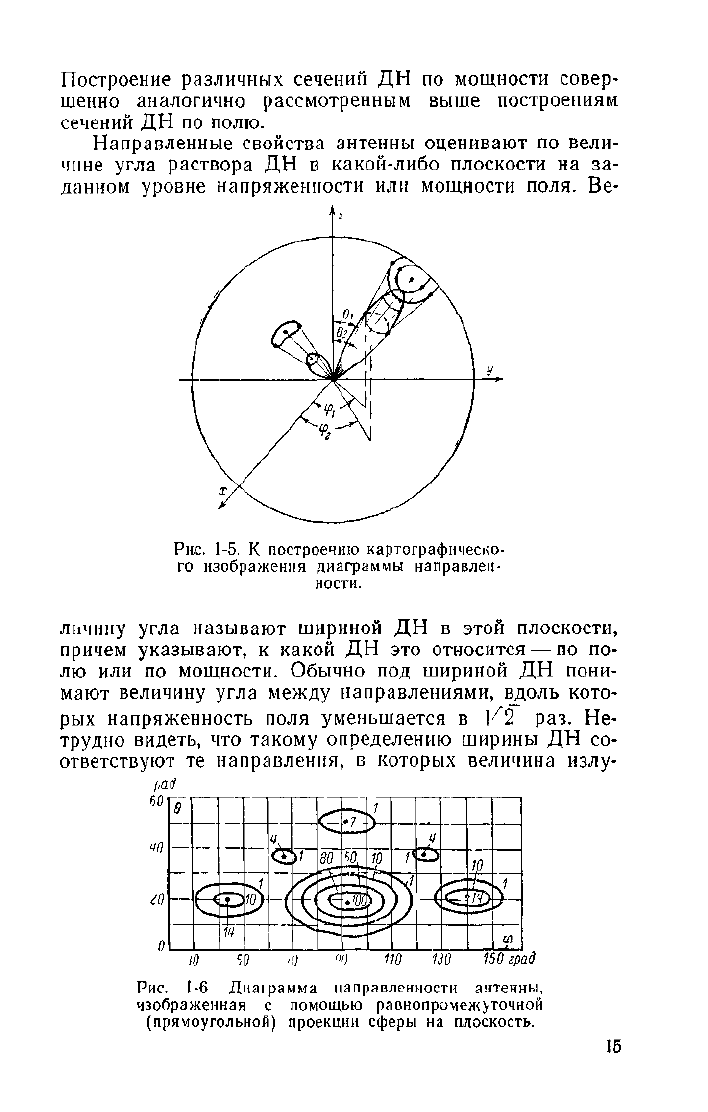
Рис.
1-5. К построению картографическо-
го изображения диаграммы направлен-
ности.
личину угла называют шириной ДН в этой плоскости,
причем указывают, к какой ДН это относится — по по-
лю или по мощности. Обычно под шириной ДН пони-
мают величину угла между направлениями, вдоль кото-
рых напряженность поля уменьшается в V
е
! раз. Не-
трудно видеть, что такому определению ширины ДН со-
ответствуют те направления, в которых величина излу-
f,ad
Рис.
1-6 Диа1рамма направленности антенны,
изображенная с помощью равнопромежуточной
(прямоугольной) проекции сферы на плоскость.
15
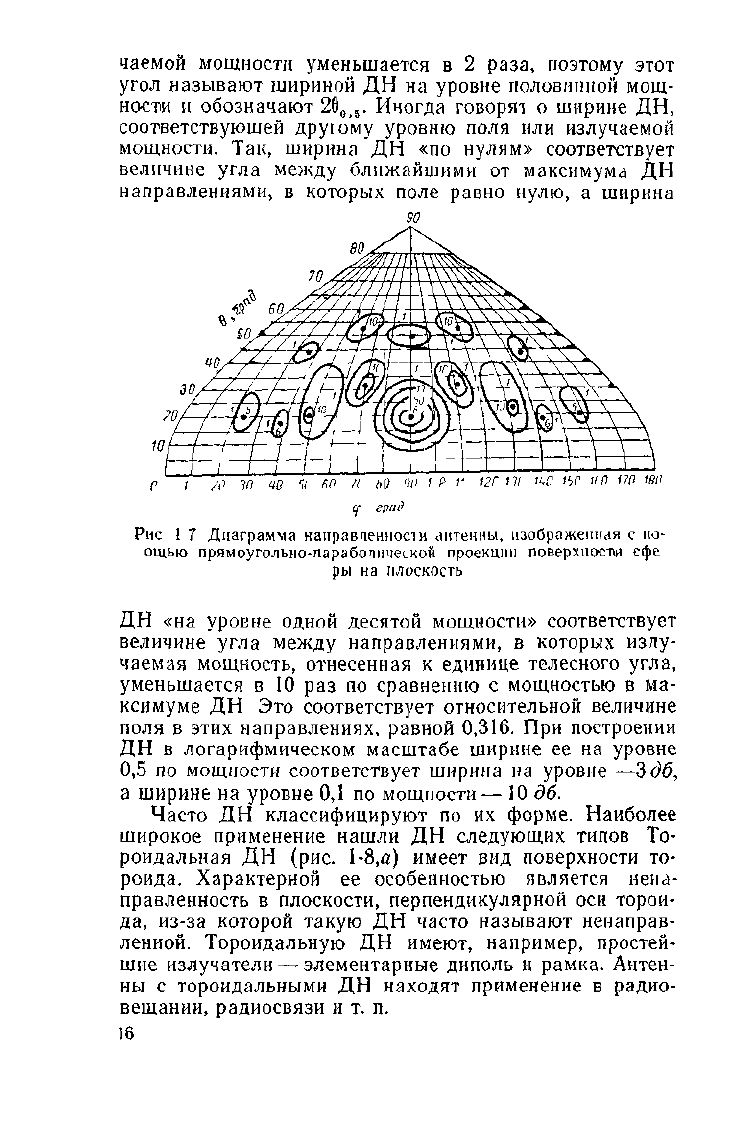
чаемой мощности уменьшается в 2 раза, поэтому этот
угол называют шириной ДН на уровне половинной мощ-
ности и обозначают
26
0)5
.
Иногда говорят о ширине ДН,
соответствующей другому уровню поля или излучаемой
мощности. Так, ширина ДН «по нулям» соответствует
величине угла между ближайшими от максимума ДН
направлениями, в которых поле равно нулю, а ширина
if град
Рис 1 7 Диаграмма направценности антенны, изображенная с по-
ощью прямоугольно-параболической проекции поверхности сфе
ры на плоскость
ДН «на уровне одной десятой мощности» соответствует
величине угла между направлениями, в которых излу-
чаемая мощность, отнесенная к единице телесного угла,
уменьшается в 10 раз по сравнению с мощностью в ма-
ксимуме ДН Это соответствует относительной величине
поля в этих направлениях, равной 0,316. При построении
ДН в логарифмическом масштабе ширине ее на уровне
0,5 по мощности соответствует ширина на уровне —Здб,
а ширине на уровне 0,1 по мощности— 10 дб.
Часто ДН классифицируют по их форме. Наиболее
широкое применение нашли ДН следующих типов То-
роидальная ДН (рис.
1-8,а)
имеет вид поверхности то-
роида. Характерной ее особенностью является нена-
правленность в плоскости, перпендикулярной оси торои-
да, из-за которой такую ДН часто называют ненаправ-
ленной. Тороидальную ДН имеют, например, простей-
шие излучатели — элементарные диполь и рамка. Антен-
ны с тороидальными ДН находят применение в радио-
вещании, радиосвязи и т. п.
16
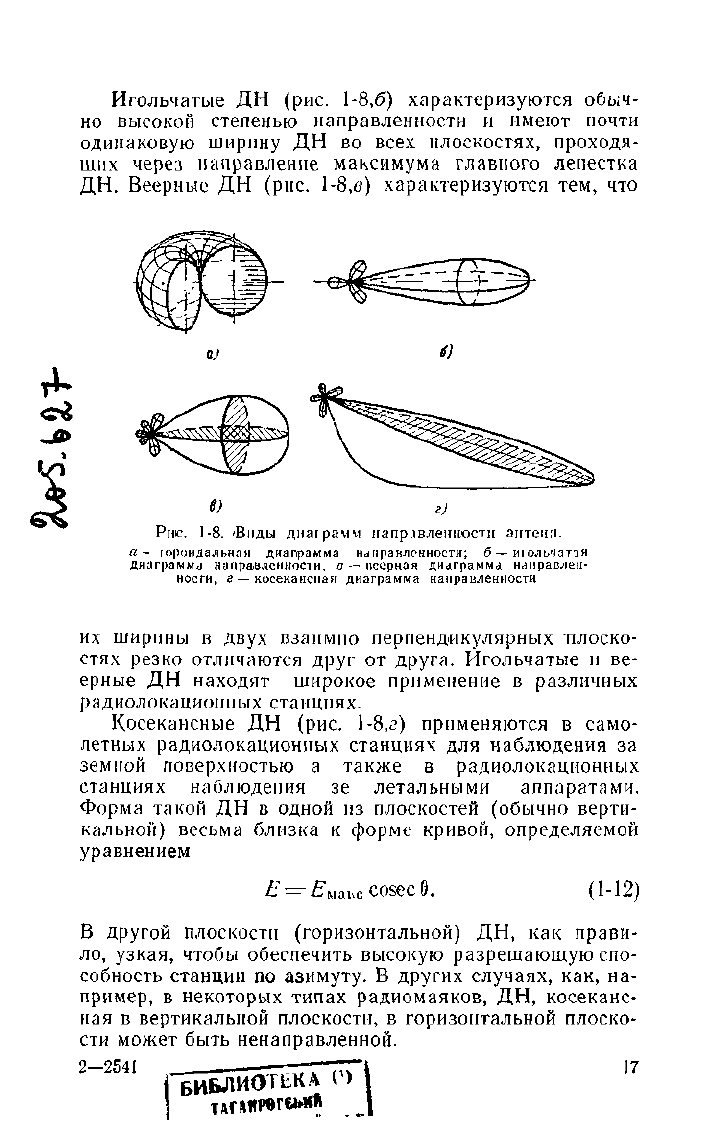
Игольчатые
ДН (рис. 1-8,6)
характеризуются обыч-
но высокой степенью направленности
и
имеют почти
одинаковую ширину
ДН во
всех плоскостях, проходя-
щих через направление максимума главного лепестка
ДН. Веерные
ДН (рпс. 1-8,в)
характеризуются
тем, что
в)
г)
Ршс.
1-8.
Виды диаграмм направленности антенн.
а- юроидальнан диапрамма направленности;
б
— июльчаття
диаграмма направленности,
в
— веерная диаграмма направлен-
ности,
г —
косекансная диаграмма направленности
их ширины
в
двух взаимно перпендикулярных 'плоско-
стях резко отличаются друг
от
друга. Игольчатые
и ве-
ерные
ДН
находят широкое применение
в
различных
радиолокационных станциях.
Косекансные
ДН (рис. 1-8,г)
применяются
в
само-
летных радиолокационных станциях
для
наблюдения
за
земной поверхностью
а
также
в
радиолокационных
станциях наблюдения
зе
летальными аппаратами.
Форма такой
ДН в
одной
из
плоскостей (обычно верти-
кальной) весьма близка
к
форме кривой, определяемой
уравнением
Е
=
Е
ыаъс
cosecS.
(1-12)
В другой плоскости (горизонтальной)
ДН, как
прави-
ло,
узкая, чтобы обеспечить высокую разрешающую спо-
собность станции
по
азимуту.
В
других случаях,
как, на-
пример,
в
некоторых типах радиомаяков,
ДН,
косеканс-
ная
в
вертикальной плоскости,
в
горизонтальной плоско-
сти может быть ненаправленной.
2—2541
БИБЛИОТЕКА
П \
тАгаярвгемс*
\
17

Помимо амплитудной ДН, отображающей изменение
модуля функций М
в
и
JV^
В пространстве, для более пол-
ной характеристики поля излучения антенны строят гра-
фики изменения аргументов этих функции, которые на-
зывают фазовыми диаграммами антенны
Для многих антенн фазовая диаграмма в пределах
главного лепестка остается постоянной при изменении
углов б и ф, а при переходе от лепестка к лепестку ме-
няется скачком на угол л Следует отметить, что в об-
щем случае фазовая диаграмма может иметь сложную
форму Так, например, фазовая диаграмма некоторых
рупорных антенн имеет форму, близкую к форме по-
верхности второго порядка
Если поверхность равных фаз (фронт волны) пред-
ставляет собой поверхность сферы, то центр этой сферы
называют ф азов ы м центром антенны Для того
чтобы антенна имела фазовый центр, функция arg./V
должна иметь вид
arg
yv
=
a.
sin
б
cos
tp
-J-
p
sin
6
sin
<p
-[-
Y
cos
6
f- S, (1-13)
где a, p\ у и
б —
постоянные коэффициенты
Координаты фазового центра при этом будут
-
Многие типы антенн не имеют фазового центра, и в этом
случае на практике обычно подбирают сферу, ко-
торая в некотором секторе углов излучения (обычно
только в пределах главного лепестка) наилучшим обра-
зом аппроксимирует фронт волны Центр этой сферы
называют центром излучения антенны
Коэффициент направленного действия (КНД), как и
ширина ДП, является мерой концентрации электромаг-
нитной энергии в пространстве, которое осуществляется
антенной В литературе часто встречаются два совер-
шенно эквивалентных друг другу определения КНД
Первое определение КНД —это число, показывающее,
во сколько раз необходимо увеличить мощность излуче-
ния антенны при переходе от направленной антенны
к абсолютно ненаправленной ', при условии сохранения
1
Абсолютно ненаправленный излучатель элсктромапшгных
волн имеющий ДН в виде поверхности сферы, в природе существо
вать не может Простейший ичлучатсль, которым является ^темен-
тарный вибратор, уже имеет направленность
18

одинаковой напряженности поля в точке приема при
прочих равных условиях:
i-nanp
при условии
-Епршпр
=
£папр
в точке приема.
Второе определение: КНД
—
это число, показываю-
щее,
во сколько раз мощность, излучаемая антенной
в данном направлении, отнесенная к единице телесного
угла, больше мощности излучения абсолютно ненаправ-
ленной антенны, отнесенной к единице телесного угла,
при условии равенства полных мощностей, излучаемых
обеими антеннами:
D(f,b) = ^L.
t
(Мб,
471
здесь Я (0,
<р) —
мощность, излученная антенной в направ-
лении, определяемом уигами 6 и <?, и
от
несенная к единице
телесного угла, Р
ь
— полная мощность, излученная антен-
ной.
Иногда при определении КНД сравнение производят
не с ненаправленным излучателем, а с некоторой антен-
ной, принятой за эталон:
Я
А
(9,у)
^[РЖ!)}'
(М7)
где Р
А
—
мощность, излученная антенной в направле-
нии 6, ф, отнесенная к единице телесного угла;
Р
0
—
мощность излучения эталонной антенны, также
отнесенная к единице телесного угла.
КНД антенны £>ль определенный по отношению
к эгалонной антенне 1, может быть пересчитан в КНД
антенны D
A
2, определяемый по отношению к эталонной
антенне 2, по формуле
где D
2
\ — КНД второй эталонной антенны относительно
первого эталона.
Из (1-16) видно, что график изменения КНД в про-
странстве отличается от ДН по мощности лишь посто-
янным множителем, не зависящим от координат. Ма-.
2*
19

ксимальная величина КНД достигает значений от еди-
ниц (слабонаправленные антенны) до нескольких десят-
ков и даже сотен тысяч (антенны с очень узкой ДН).
Коэффициент полезного действия антенны (к. п. д.).
Не вся подводимая к антенне мощность излучается в ви-
де энергии электромагнитных волн. Часть подводимой
мощности будет теряться в антенне. Для характеристи-
ки потерь в антенне вводят коэффициент полезного дей-
ствия антенны (ц), равный отношению мощности, излу-
ченной антенной в пространство (PJ, к мощности, ко-
торая к ней подводится
{РА)'-
1
=
5
L
-
(MS)
Коэффициент усиления антенны (КУ). Две антенны,
имеющие одинаковые ДН, а следовательно, и одинако-
вый КНД, при равной подводимой мощности могут соз-
давать в одинаково расположенных относительно антенн
точках приема различные напряженности поля. Это обу-
словлено различной величиной потерь энергии в антен-
нах. Чтобы учесть при наличии потерь изменение напря-
женности поля в точке приема, вводят понятие коэффи-
циента усиления антенны— КУ. Определение КУ ана-
логично определению КНД, только рассматривается
полная излучаемая мощность реальной антенны и пол-
ная излучаемая мощность эталонной антенны, имеющей
к. п. д., равный 100%.
Таким образом, можно дать КУ следующее опреде-
ление: КУ
—
это число, показывающее, во сколько раз
мощность, излучаемая реальной антенной в данном на-
правлении, отнесенная к единице телесного угла, боль-
ше мощности, излучаемой в единице телесного угла, аб-
солютно ненаправленной антенны, с к. п. д., равным
100%,
при условии равенства подводимых к антеннам
мощностей. Из этого определения сразу следует, что КУ
равен:
G(6,
?)^ф(Ь,
?
). (1-20)
Обычно, если нет специальных оговорок, под КНД и
КУ понимается их максимальное значение, т. е.
u
=
L)
м шс
;
"
=
-^мш(с'П-
20
(1-21)
