Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч.

Подождите немного. Документ загружается.

297

Отже,

),(

ttK

′′′

є невипадковою функцією двох аргументів t

),(

ttK

′′′

зменшується зі збільшенням різниці t

– t

для випад-

кового процесу X

(t) повільніше, ніж для випадкового процесу X

(t).

При цьому:

1) )()(),(

tDtKttK

xxxx

′′′

; при ttt

;

),(),(

1221

ttKttK

xxxx

′′′′′′

= ;

3) 0),(

≥

′′′

ttK

Тісноту лінійної залежності двох перерізів випадкового про-

цесу X(t) вимірюють нормованою кореляційною функцією, яка

дорівнює

)()(

),(

);(

ttK

ttr

σ⋅σ

= . (583)

При цьому:

1) 1),( =ttr

при ttt

;

),(),(

1221

ttrttr

= ;

1),(

≤ttr

Приклад 1. Випадкова функція має такий вигляд:

0, >⋅=

λ−

teXY

де Х — випадкова величина, що має закон розподілу

),;( σaN

де a > 0.

Визначити:

);(),,(),(),(),(

2121

ttrttKttDtM

yyyyy

Розв’язання. Випадкова величина Х має загальний нормальний закон

розподілу зі значеннями параметрів

0)( >

axM

)(x

ttt

aeXMeXeMtM

λ−λ−λ−

=== )()()(

;

ttt

eXDeXeDtD

λ−λ−λ−

σ===

)()()(

;

etDt

λ−

⋅σ==σ )()(

;

′

−

′

−

′

= )))())((((),(

YMYYMYMttK

=−−=

λ−λ−λ−

λ−

))())(((

2211

XMeXeXMeXeM

ttt

=−=−−=

+λ−+λ−

)()(

))(())())(((

2121

XMXMeXMXXMXMe

tttt

298

)(

+λ−

σ=

Отже,

=),(

ttK

)(

+λ−

Оскільки

,)(

λ−

⋅σ=σ

,)(

λ−

=σ

то

)()(

);(

)(

⋅σ⋅⋅σ

σ⋅σ

λ−λ−

+λ−

ttK

ttr

Отже,

1);(

=ttr

3. Марковські випадкові процеси.

Ланцюги Маркова

Серед випадкових процесів, що широко застосовуються для

створення стохастичних (імовірних) моделей, котрі описують

процеси функціонування певних систем технічного, економічно-

го, екологічного та соціального профілю, центральне місце нале-

жить марковським.

Випадковий процес X(t) називають марковським, якщо за

будь-якого можливого значення часу t = t

значення випадкової

величини x(t

) не залежить від того, яких значень ця величина

набувала для t < t

, тобто, процес у момент часу t = t

не залежить

від його поведінки в більш ранні моменти часу t < t

Марковський процес X(t) називають однорідним, якщо зако-

номірності його поведінки на будь-якому проміжку часу

∆

T не

залежать від розміщення цього інтервалу на часовій осі.

Нехай X(t) — однорідний марковський процес із обмеженим,

або зліченним, числом можливих станів і = 0, 1, 2, 3, ..., n, ...

Якщо аргумент t набуває лише значення 0, 1, 2, 3, ..., то в

цьому разі матимемо послідовність переходів

→→ )1()0( xx

.....)3()2( →→→ xx

Такий процес послідовностей переходів називають ланцюгом

Маркова.

При розробленні теорії ланцюгів Маркова часто дотримують-

ся іншої термінології, а саме: розглядається певна фізична систе-

ма S, яка в кожний момент часу може перебувати в одному з не-

сумісних станів A

, A

, ..., A

, ... і змінювати свій стан лише в

моменти часу t

, t

, ..., t

, ...

Процес переходу систем S утворює ланцюг Маркова, якщо

ймовірність перейти в стан A

в момент часу t (t

< t < t

k+1

) зале-

жить лише від того, в якому стані система перебувала в момент

299

часу t

′

k–1

< t

′

< t

), і не залежить від стану системи в більш раніш-

ні моменти часу.

Імовірності переходу зі стану A

в стан A

в момент часу t поз-

начають через p

(t).

Повна ймовірна картина всіх можливих переходів систем із

одного стану в інший за умови, що число всіх станів дорівнює N,

безпосередньо описується матрицею ймовірностей переходу

⎟

⎠

⎞

⎜

⎝

⎛

=π

)(........)()(

....................................

)(........)()(

)(.......)()(

22221

11211

tptptp

NNNN

. (584)

Якщо p

(t) не залежить від часу, то ланцюг Маркова називають

однорідним і тоді p

(t) = p

= const. А тому для однорідних ланцюгів

Маркова матриця ймовірностей переходу набуває такого вигляду

⎟

⎠

⎞

⎜

⎝

⎛

=π

NNNN

ppp

........

..............................

........

.......

22221

11211

. (585)

Для кожного рядка матриць (584), (585) виконується рівність

∑∑

ijij

ptp

1)(

. (586)

Це свідчить про те, що, перебуваючи в будь-якому можли-

вому стані A

у фіксований момент часу t, cистема обов’язково

перейде з певною ймовірні-

стю в будь-який інший мо-

жливий стан A

або зали-

шиться в цьому самому

стані. А ці події є несуміс-

ними й утворюють повну

групу.

Матрицю

(585) назива-

ють ще матрицею ймовірнос-

тей однокрокового переходу

системи. Якщо позначимо

множину всіх можливих ста-

нів системи через

Ω

= (

,...,

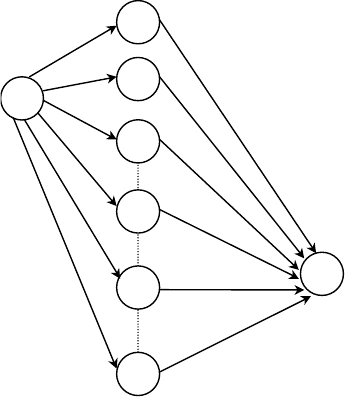
), то ймо-

вірність переходу системи зі

стану

у стан

за два кро-

і1

і2

і3

іі

іj

іN

Рис. 162

300

ки можна схематично показати на рисунку 162.

Отже, ймовірність того, що система зможе перейти за два

кроки зі стану

до стану

, дорівнюватиме:

()

=++++++=

NjiNjjijjijijiij

ppppppppppP ......

332211

∑

kjik

для

NjNi ,1,,1 ==

. (587)

Вираз (587) є елементом матриці

, який дістанемо при мно-

жині i-го рядка матриці

на її j-й стовпчик.

Імовірність переходу системи зі стану

у стан

за n кроків

обчислюється за формулою:

∑

−

kjik

ppp

)1()(

, (588)

де

)(n

— елемент матриці

Матрицю

називають n-кроковою матрицею переходу з од-

ного стану в інший.

Імовірну картину переходу системи з одного стану в інший

наочно можна зобразити з допомогою так званих орієнтованих

імовірнісних графів, де кожний стан системи показано точкою

(вершина графа), а можливі переходи з цього стану — ймовірніс-

ними ребрами. Число станів на

графі дорівнює числу вершин.

Приклад 2. За заданою матрицею ймовірностей переходу

деякої системи

⎟

⎠

⎞

⎜

⎝

⎛

=π

5,01,04,0

2,05,03,0

7,02,01,0

побудувати орієнтований імовірний граф.

Розв’язання. За умовою задачі система має три стани ω

, ω

, от-

же, граф матиме три вершини. Ймовірності переходу системи з одного

стану в інший наведені в кожному

рядку матриці π.

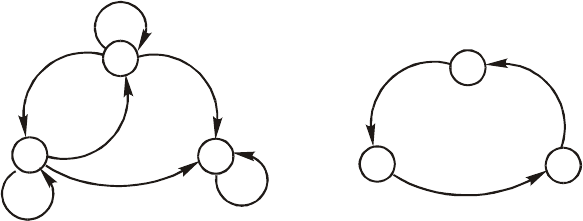
Імовірний граф матиме такий ви-

гляд (рис. 163).

Використання ймовірних графів

можливе лише у тому разі, коли кіль-

кість станів систем є невеликою.

Уже за числа вершин (станів) 10 і

більше рисунок

набуває складної

структури.

0,1

0,5

0,3

0,2

0,4

0,2

0,1

0,7

0,5

Рис. 163

301

4. Класифікація ланцюгів Маркова

Якщо серед можливих станів систем, що описує ланцюг Мар-

кова, є хоча б один, в якому система залишиться, коли перейде в

нього на певному кроці функціонування, то такий ланцюг нази-

вають поглинальним ланцюгом Маркова.

Матриця однокрокового переходу для поглинаючої системи з

трьох станів, наприклад, може мати такий вигляд:

⎟

⎠

⎞

⎜

⎝

⎛

=π

100

4,02,04,0

5,03,01,0

Імовірний граф цієї матриці зображено на рис. 164.

0,2

0,3

0,4

0,5

Рис. 164

Рис. 165

Тут

є поглинаючим станом цієї системи.

Якщо в кожний можливий стан система може перейти через

певний інтервал часу, то такий ланцюг Маркова, що моделює цей

процес, називають циклічним.

Матриця циклічного ланцюга Маркова може мати для випад-

ку трьох можливих станів системи такий вигляд:

⎟

⎠

⎞

⎜

⎝

⎛

=π

001

100

010

Граф цієї матриці буде таким (рис. 165).

Ланцюг Маркова називається регулярним, якщо існує таке ціле

число k (k > 0), що перехід системи з будь-якого можливого ста-

ну в інший може здійснитися за k кроків.

302

Так, наприклад, для чотирьох можливих станів системи мат-

риця однокрокового переходу може мати такий вигляд:

⎟

⎠

⎞

⎜

⎝

⎛

=π

1,04,01,04,0

2,02,05,01,0

4,01,02,03,0

2,05,01,02,0

Графом для цієї матриці буде рис. 166.

0,2

0,4

0,1

0,3

0,4 0,2

0,2

0,1

0,5

0,1

Рис. 157

Циклічні та регулярні матриці називають ергодичними.

Найширшого використання для розв’язування прикладних за-

дач набули регулярні ланцюги Маркова.

5. Регулярні ланцюги Маркова.

Стаціонарні ймовірності.

Матриця вартостей

Для регулярних ланцюгів Маркова було доведено, що незале-

жно від початкового стану, в якому перебувала система, ймовір-

ність перебування її в певному можливому стані прямує до де-

якої сталої величини при збільшенні кількості кроків k.

Тобто, при k

→

∞

const

)(

=→

bp .

Імовірності b

(j = 1, 2, ..., N) називають стаціонарними.

Отже,

303

⎟

⎠

⎞

⎜

⎝

⎛

==π

∞→

bbb

...

............

...

lim

Тут

∑

, В — матриця стаціонарних імовірностей.

Таким чином, можна зробити висновок: якщо відомі

, В і при

цьому

)...,,,(

21 N

bbbb =

, а також задано

)...,,,(

21 N

aaaa

— век-

тор початкових можливих станів системи, то виконуються рівності:

.limlim bBaaa

==π=π

∞→∞→

Можна довести, що коли

є регулярною матрицею і

— ве-

ктор стаціонарних імовірностей, то

=π . (589)

І справді, оскільки

→π

, то

π=ππ=π⋅π=π

−

∞→

−

∞→∞→

limlimlim

бо

,lim

=π

−

∞→

=π

∞→

lim

Отже, маємо

В = π В. (590)

Таким чином, для будь-якого рядка рівняння (590) виконува-

тиметься рівність

=π . (591)

Отже, для визначення стаціонарних імовірностей регулярного

ланцюга Маркова необхідно розв’язати систему рівнянь

⎪

⎩

⎪

⎨

⎧

π=

∑

(592)

Приклад. Знайти стаціонарні ймовірності для регулярної

матриці

⎟

⎠

⎞

⎜

⎝

⎛

=π

5,04,01,0

3,05,02,0

6,01,03,0

Розв’язання. Використовуючи систему (650), дістаємо:

304

→

⎪

⎩

⎪

⎨

⎧

=++

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

5,04,01,0

3,05,02,0

6,01,03,0

321

bbb

→

⎪

⎩

⎪

⎨

⎧

=++

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

5,04,01,0

3,05,02,0

6,01,03,0

321

bbb

→

⎪

⎩

⎪

⎨

⎧

=++

++=

→

,5,04,01,0

,3,05,02,0

,6,01,03,0

321

3213

3212

3211

bbb

bbbb

⎪

⎩

⎪

⎨

⎧

=++

=−+

=+−

−

,05,04,01,0

,03,05,02,0

,06,01,07,0

321

bbb

Розв’язуючи одержану систему, маємо:

⎟

⎠

⎞

⎜

⎝

⎛

, тобто

При переході системи з одного стану в інший за один крок її

функціонування, а також у разі, коли система залишиться в тому

самому стані, в якому вона перебувала, вводиться так званий ко-

ефіцієнт вартості

, що інформує про витрати, які пов’язані при

переході системи зі стану

у стан ω

за один крок.

Щоб визначити загальні витрати, які можна очікувати за

кроків роботи системи, використовується матриця вартостей

⎟

⎠

⎞

⎜

⎝

⎛

NNNNN

rrrr

...

.......................

...

321

2232221

1131211

. (593)

Елементи матриці

R можуть набувати додатних, нульових та

від’ємних числових значень. Якщо умовно позначимо через

(n)

сумарні витрати після

n кроків переходів системи, починаючи із ω

стану, тоді

()

))(...,),(,)(()(

nvnvnvnv

′

буде вектором сумарних

витрат за

n кроків для кожного з ω

станів (i = 1, 2, ..., N) системи.

Якщо система досягла

стану, то очікувану винагороду після

всіх переходів можна подати як

)1(

−

nvr

iij

, де

— винагорода,

яку дістанемо при переході системи із

стану в ω

стан за один

крок, а

)1( −nv

— очікувана винагорода, яку матимемо за решту

n – 1 кроків.

305

Ураховуючи те, що ймовірність переходу системи зі стану ω

до

стану

за один крок дорівнює p

, то сумарна очікувана вартість

(винагорода) за

n переходів системи, починаючи зі стану ω

, буде

∑

−+

∑

ijj

ijiji

pnvprnv

)1()(

(594)

або

∑

−+=

ijjii

pnvgnv

)1()(

, (595)

де

∑

ijiji

prg

Оскільки рівняння (594), (595) виконується для всіх

Ni ,1= , то

(595) можна записати у векторно-матричній формі

)1()(

−

nvgnv

, (596)

тут )...,,,(

21 N

gggg

′

, де g

— елементи головної діагоналі мат-

риці

′

⋅

;

′

— транспонована матриця вартостей R.

Компоненти вектора )(nv

визначають із векторно-матричного

рівняння

)0()...()(

)()1(32

vgEnv

π+π++π+π+π+=

−

, (597)

де Е — одинична матриця,

)0(v

— вектор винагороди за n = 0

кроків.

Приклад. Фермер придбав новий трактор, який може пе-

ребувати в одному з трьох несумісних станів: ω

— трак-

тор працює добре, тобто не потребує жодних втручань,

пов’язаних із витратами; ω

— трактор може бути викори-

станий у роботі, але потребує дрібного ремонту, який, у

свою чергу, вимагає певних витрат; ω

— трактор перебу-

ває в нероботоздатному стані, що відбивається на прибут-

ках фермера.

Матриця ймовірностей переходу трактора з одного стану в

інший за один крок (за 1 місяць) має такий вигляд:

⎟

⎠

⎞

⎜

⎝

⎛

=π

78,002,02,0

1,06,03,0

04,006,09,0

За заданою матрицею вартостей

306

⎟

⎠

⎞

⎜

⎝

⎛

−

5010100

2040150

1050200

Оцінити ефективність роботи трактора за три робочих

місяці. Елементи матриці вартостей r

вимірюються в

гривнях.

При цьому

)000())0((

′

Розв’язання. З рівняння (597) для n = 3 дістанемо

)0()()3(

vgEv

π+π+π+=

. (598)

Визначимо координати вектора

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−−−

⎟

⎠

⎞

⎜

⎝

⎛

′

8,182,152,33

316789

6,886,1366,182

502010

104050

100150200

78,002,02,0

1,06,03,0

04,006,09,0

Таким чином,

маємо:

⎟

⎠

⎞

⎜

⎝

⎛

−

8,18

6,182

Рівняння (598) перепишемо в такому вигляді

⎟

⎠

⎞

⎜

⎝

⎛

−

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

8,18

6,182

78,002,02,0

1,06,03,0

04,006,09,0

78,002

,02,0

1,06,03,0

04,006,09,0

100

010

001

)3(

→

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

78,002,02,0

1,06,03,0

04,006,09,0

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

→

9,47

6,268

81,507

5,43

5,108

6,157

2,23

1,93

61,167

8,18

6,182

)3(

Таким чином, маємо:

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

9,47

6,268

81,507

)3(

Жлуктенко В. І., Наконечний С. І., Савіна С.С. Теорія ймовірностей і математична статистика: У 2-х ч. - Ч. ІІ. Математична статистика

Подождите немного. Документ загружается.