Жиркин Ю.В. Надежность, эксплуатация и ремонт металлургических машин. Учебник. Часть 1
Подождите немного. Документ загружается.

σ
µ
−
=
t
u
где
ϕ
(u) - табличное значение (см. табл.2).
1
=
µ
)(tP
5.0
=
σ
1
=
σ
2=
σ
0
a
t
)(tf
5.0
1
=
σ
1
=
µ
1
2
=
σ
2
3
=
σ
0
б
πσ
2*
1
1
σ
2
σ
3
σ
1
σ
2
σ
3
σ
1
=
µ
2
=
µ
)(t
λ
0t
5.0
=
σ
1
=
σ
2
=
σ
1
=
σ
в
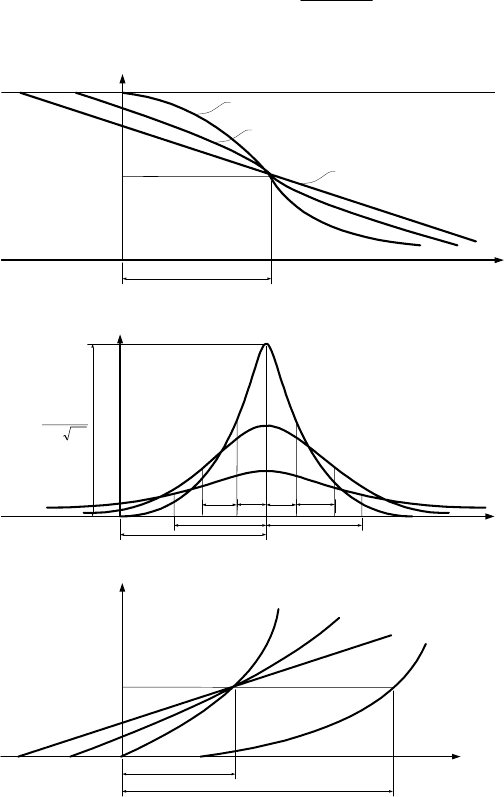
Рис.4.3. Нормальное распределение:
а – вероятность безотказной работы;
б – плотность вероятности отказов;
в – интенсивность отказов
31
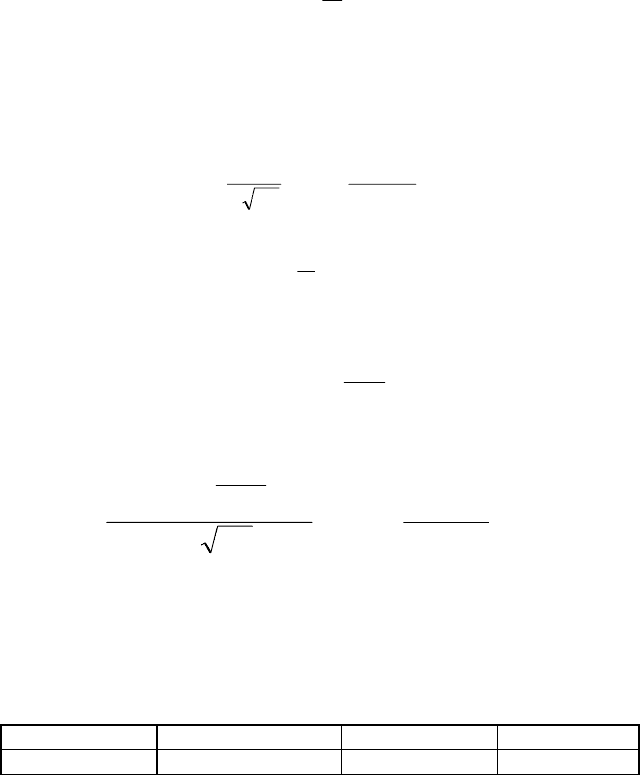
средняя наработка
фициент вариации
Числовые характеристики распределения:
T=M
ξ=µ;
дисперсия
D=
σ
2
;
коэф
;
µ
σ
ν
=
коэффициент асимметрии А =0;
эксце E =0.
говоря, в теории надежности должен использоваться
усеченный (слева) нормальный закон (рис.4.4) с плотностью
сс
Строго
ft
ct
() exp
()
,=⋅−
−
⎡
⎣
⎢
⎦
⎥
σπ
σ
2
2
2
так как наработки являются неотрицательными величинам, где
⎤
µ
2
(4.9)
1C Ф .
µ
⎡
⎤
⎛⎞
σ
=− −
⎜⎟
⎢
⎥
⎝⎠
⎣
⎦
Вероятность безотказной работы
(4.10)
⎥
⎤
⎢
⎡
⎟
⎞
⎜
⎛
−
Φ−⋅=
σ
µ
t
CtP 5,0)(
⎦
⎣
⎠⎝
; (4.11)
отказов Интенсивность
()
()
;exp
-t
Ф50
2
1
⎟
⎞
⎜
⎛
−
−⋅
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−
=
−
µ
σ
µ
λ
t
t
2
2
2
⎠
⎝
⋅
σ
πσ
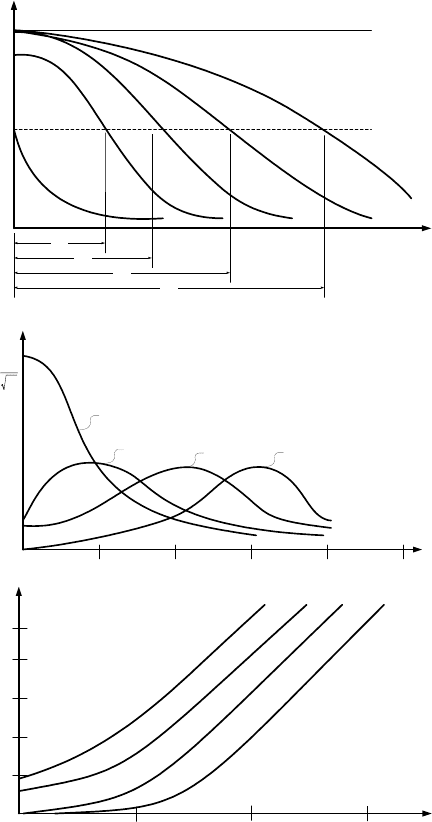
На графике рис.4.4 видно, что с увеличением срока эксплуа-
тации интенсивность отказов растет
,
⎟
⎜
. (4.12)
, т.е. снижается надежность
издел
µ
рактически совпадают с нормальным распределе-
нием
µ/σ 1 2 3
ия.
Для усеченного нормального распределения при (
/σ)>3 ха-
рактеристики п
C 1,189 ,023 1,001 1
32
P(t)
t
0
1
0,5
µ=1
µ=2
µ=3
µ=4
f(t)
π
2
С
t
1234
µ=0
µ=1
µ=2
µ=3
5
t
0
2
4
)( t
λ
1
3
6
5
4
2
µ=0 µ=1 µ=2 µ=3
Рис.4.4. Усеченное (слева) нормальное распределение:
а - вероятность безотказной работы;
б – плотность вероятности отказов;
в – интенсивность отказов
33

Поэтому широко используются более простые зависимости
нормального распределения для стареющих элементов.
Пример 4.3. Ролики транспортного рольганга имеют наработ-
ки, распределенные по нормальному закону с математическим ожи-
данием
µ =350 сут и средним квадратичным отклонением σ=50 сут.
1. Найти вероятность безотказной работы роликов на 300
сут.
2. Построить график интенсивности отказов.
3. Если вероятность появления отказов в процессе эксплуа-
тации не должна превышать 20%, то через какой период времени
необходимо проводить их замену?
Решение.
Вероятность безотказной работы находим по формуле (4.6).
()
841,0341,05,0
50
350300
5,0300 =+=
⎟
⎠
⎞
⎜
⎝
⎛
−
−==
ФtP
.
Функцию Лапласа
Φ((t-µ)/σ) находим из табл. 1 прил. Б для
функции нормированного нормального распределения. Построе-
ние графика интенсивности отказов осуществляем, используя
формулу (4.8).
Так =0,2, то
нормального рас-
прил.Б. Следовательно, за-
мену
рнира универсального шпинделя
альным распределением с математическим
ожиданием
µ=40 сут и средним квадратичным
Определить, при какой величине
µ (σ=const) и при какой ве-
личине
σ (µ=const) будет обеспечена в меж
сут вероятность отказа Q (t=30)=0 .
анной вероятности отказа
=q
u
(табл.3, прил.Б), тогда
как из условия задачи вероятность отказа Q(t)
вероятность безотказной работы P(t)=0,8.
Тогда табличное значение квантили
8,0
u
пределения равно (-0,842) из табл.3.
роликов необходимо проводить через
08
350 50 350 0 842 50 308
,
tu , сут.=−⋅=− ⋅=
Пример 4.4. Наработки ша
описываются норм
отклонением σ=20
сут.
ремонтный период t
p
=30
,1
Решение.
Для обеспечения зад
28,1
9,0
−=
34

128
t
.,
µ
σ
−
=−
отсюда
6,552028,13028,1t
=
×
+
=
+
=
σ
µ
сут;
8,7
28,1
4030t
28,1
=
−
=
−
−=
µ
σ
сут.
довательно, для обеспечения вероятности безотказной
работы P(t=30)=0,9 необходимо выполнить мероприятия либо по
повышению средней наработки шарнира универсального шпинде-
ля в 1,4 раза, либо по снижению стандарта до 7,8 сут.
логического процесса получения
материала, процесса изго-
товления изделия и правил его технической эксплуатации.
значений среднего квад-
ратич о чисто технических, но и
орган
4.4. Логарифмически нормальный закон
Логарифмически нормальное распределение – распределе-
ние двухпараметрическое (рис.4.5) с плотностью распределения
Сле
Как правило, повышение средней наработки связано с суще-
ственными затратами, направленными на повышение износостой-
кости.
Величина среднего квадратичного связана с нарушениями
техно
Поэтому достижение более низких
ного является следствием не тольк
изационных мероприятий.
()
;
2
)(
2
⎥
⎤
××
=
σ
πσ
t
tf
(4.13)
пределения.
Вероятность безотказной работы
ln
exp
1
2
⎢
⎡
−
−
mt
⎦⎣
где
σ и m - параметры рас
ln
5,0)(
⎟
⎞
⎜
⎛
−
Φ−=
mt
tP
.
⎠
⎝
σ
(4.14)
Интенсивность отказов
)(
ln
)(
tPt
mt
t
××
⎟
⎠
⎞
⎜
⎝
⎛
−
=
σ
σ
ϕ
λ
. (4.15)
35
P(t)
0
1
а
0,8
0,6
0,4
0=
µ
1
=
µ
2
=
µ
3
=
µ
0,2
t
f(t)
t
0
б
0
=
µ
5,0
=
µ
1
=
µ
t
0
в
0
=
µ
5,0
=
µ
1
=
µ
)(t
λ
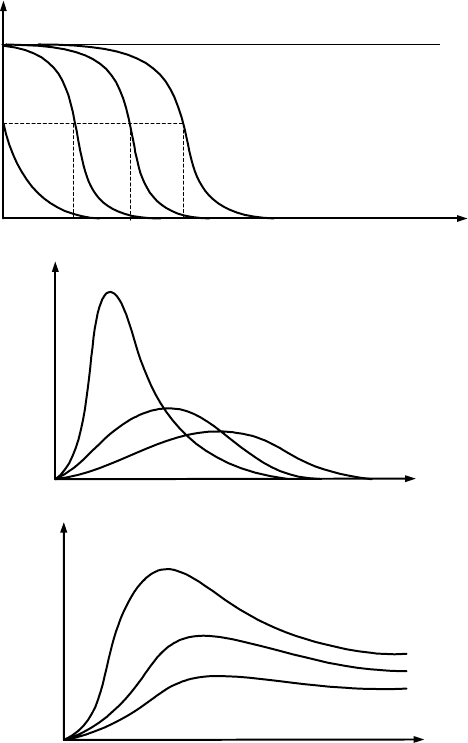
Рис.4.5. Логарифмически нормальное распределение:
а – вероятность отказов;
б – пл
в ин
Для ло ри ия характер-
но возраста е интенси ением срока экс-
плуатации.
отность вероятности отказов;
– тенсивность отказов
пределенга фмически нормального рас
и вности отказов с увеличн
36

Числовые характеристики:
средняя наработка
;
2
exp
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
σ
mT
(4.16)
дисперсия
2
(
)
;1
22
2
−=
+
σσ
eeD
m
(4.17)
коэффициент вариации
1
2
−=
σ
ν
e .
Пример 4.5. Наработка до отказа подшипника скольжения
механизма уравновешивания шпинделей имеет логарифмически
нормальное распределение с параметрами m=4,
σ=1.
1. Найти вероятность безотказной работы и интенсивность
отказов при наработке t =60 сут.
2. Определить величину средней наработки.
ные значения m,
σ и t,
получ
Решение.
Подставляя в формулу (4.14) числен
им
,464,0036,05,0
1
460ln
⎞⎛
−
5,0)60( =−=
⎟⎜
Φ−==tP
нормаль-
ного распределения.
Используя выражение (4.15), ходим интенсивность отка-
зов.
⎠⎝
где Ф
(0,04)
=0,036 из табл.1 прил.Б нормированного
на
014,0
3973,0
1
)( ==
⎠
⎝
=
λ
t
,
464,060464,0160
460ln
×××
⎟
⎞
⎜
⎛
−
ϕ
е Ф
=0,3973 из табл прил.Б.
гд
(0,04)
.2
Значение величины средней наработки находим по формуле
(4.16)
2
1
490
2
⎝⎠
T exp сут.
⎛⎞
=+=
⎜⎟
⎜⎟
37
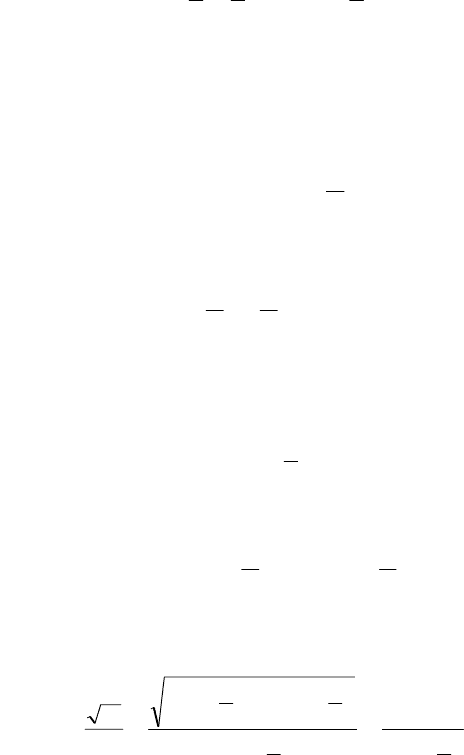
4.5. Закон Вейбулла
Закон Вейбулла - это двухпараметрическое распределение
(рис.4.6) с плотностью отказов
,exp)(
⎥
⎥
⎦
⎢
⎢
⎣
⎟
⎠
⎜
⎝
−
⎟
⎠
⎜
⎝
×=
aaa
tf
(4.18)
1
⎞
⎛
− bb
tb
⎤
⎡
⎞
⎛
t
где b - параметр формы; a - ресурсная характеристика.
Вероятность безотказной работы
.exp)(
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−=
b
a
t
tP
(4.19)
Интенсивность отказов
.)(
1−
⎟
⎞
⎜
⎛
×=
b
t
a
b
t
λ
(4.20)
⎠⎝
a
характеристики:
средн
Числовые
яя наработка
;
1
1
⎟
⎞
⎜
⎛
+Γ×= aT
(4.21)
⎠⎝
b
дисперсия
;
1
1
2
1
22
⎥
⎤
⎢
⎣
⎡
⎟
⎞
⎜
⎛
+Γ−
⎟
⎞
⎜
⎛
+Γ= aD
(4.22)
⎦
⎠
⎝
⎠
⎝
bb
коэфф
ициент вариации
.
1
1
1
1
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
=
⎟
⎠
⎞
⎜
⎝
⎛
+Γ
⎠
⎝
⎠
⎝
==
b
C
b
bb
T
D
12
1
2
⎞
⎛
⎞
⎜
⎛
+Γ
1
⎟
⎜
+Γ−
⎟
V
b
(4.23)
ν
38
)(tP
t
0
а
2
=
b
5,0
=
b
1
=
b
0,8
1
0,3
0,4
0,6
68
0,2
4
=
b
1
2
а=1
)(tf
t
0
б
1
2
⎩
⎨
⎧
=
=
4
1
b
a
⎩
⎨
⎧
=
=
2
1
b
a
⎩
= 2b
⎨
⎧
= 2a
)(t
λ
t
0
в
2>b
2
=
b
12 >> b
1
=
b
5.0
=
b
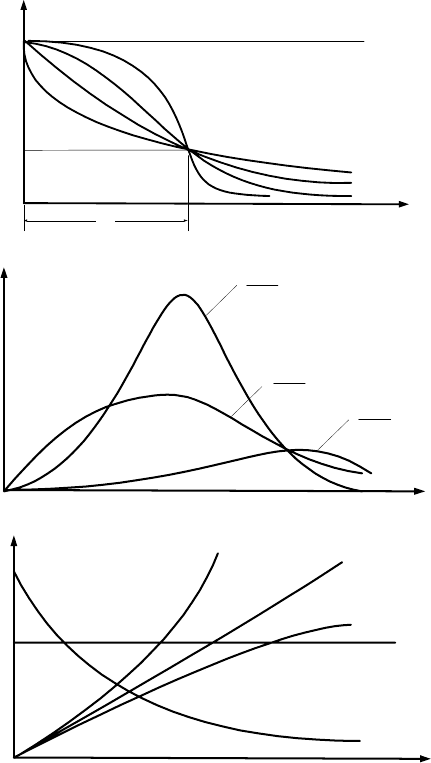
Рис.4.6. Распределение Вейбулла:
а – вероятность безотказной работы;
в; б – плотность вероятности отказо
– в интенсивность отказов
39

Для закона Вейбулла интенсивность отказов имеет различ-
ный характер изменения с течением времени в зависимости от па-
раметра b.
ая и
аспределение Вейбулла переходит в экспоненциальное распре-
делен
ние Р
При b =1 интенсивность отказов есть величина постоянн
р
ие.
Для b=2 распределение Вейбулла переходит в распределе-
елея, и интенсивность отказов описывается уравнением пря-
мой
2
)(
2
tt ×=
σ
λ
. (4.24)
Для b>2 интенсивность отказов растет с течением времени.
Если же b<1, интенсивность с течением времени снижается, что,
как указывалось выше, характерно для начального периода экс-
плуатации новых изделий.
Пример 4.6. Наработка 7 секции транспортного рольганга
имеет
1
сут.
где Г(1+1/1,9 из
абл.6. прил.Б.
распределение Вейбулла с параметрами a=60 сут, b =l,9.
Найти вероятность безотказной работы и интенсивность от-
казов при наработке t= 40 сут.
Найти среднюю
наработку на отказ.
Решение.
Подставляя исходные данные в формулу (4.19), получим
.
Интенсивность отказов находим по формуле (4.20)
629,0
60
exp)40( =
⎥
⎥
⎦
⎢
⎢
⎣
⎟
⎠
⎜
⎝
tP
40
⎞⎛
9,1
⎤⎡
−==
022,0
19,1
=
−
.
Средняя наработка на отказ в соответствии с формулой
(4.21)
6040
⎠
⎝
409,1
)40(
⎟
⎞
⎜
⎛
×==
t
λ
22,53887,060
1
160
9,1
с
T =×=
⎟
⎞
⎜
⎛
+Γ×=
⎠
⎝
) - гамма-функция, значение которой находится
т
4.6. Непараметрические классы распределений наработки
40
