Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

II.3. Stable and unstable invariant manifolds 71

(i) W

.0; '/ D j.E

(ii) j is injective, that is, x

¤ x

H) j.x

/ ¤ j.x

(iii) dim dj .x

D dim E

for all x

2 E

In precisely the same way, the unstable invariant manifold W



.0; '/ is parametrized

by E



The subsets W

and W



are immersed manifolds without boundary and without

self intersections, and in general, they are not submanifolds of R

. The tangent space

of W

.0; '/ in the point p D j.x

/ is equal to

.0; '/ D dj.x

;

so that dim T

.0; '/ D dim E

Proof of Theorem II.11 [Constructive]. Theorem II.11 is an easy consequence of

Theorem II.8 and its proof, from which we also adopt the notation. We consider

the diffeomorphism ' and the modiﬁed diffeomorphism Q' from the proof of Theo-

rem II.7 and recall the following facts:

Q'.x/ D '.x/; x 2 Q; (1)

.0; '/ Dfx j '

.x/ ! 0; j ! C1g

[

n0

n

loc

.Q//;

(2)

´ W

loc

; Q'/

Dfx jQ'

.x/ ! 0; j ! C1g (3)

Dfx j x D .x

; h.x

//; x 2 E

loc

.Q/ D

\ Q; (4)

Q'.

/ D

; (5)

Q'.

\ Q/  Q: (6)

Remark. For a given point x D .x

; h.x

// 2

, there exists, due to (3) and

(4) an integer s  0 satisfying

.x/ 2

\ Q D W

loc

.Q/:

We deﬁne the point y

.s/

2 R

.s/

´ '

s

BQ'

.x/ 2 W

.0; '/;

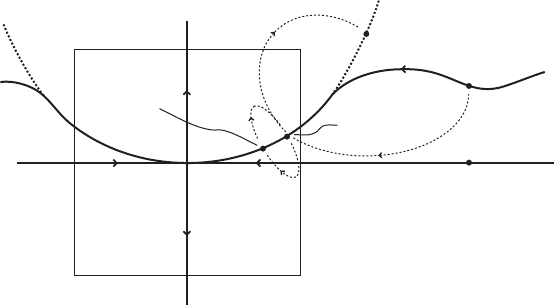
72 Chapter II. Invariant manifolds of hyperbolic ﬁxed points



.0; '/

.s/

.x/

sC1

.x/

1

s

Figure II.9. Illustrating the proof of the theorem by S. Smale.

where we have used the deﬁnition (2) of the stable manifold. As long as Q'

.x/ lies

in Q the point y

.s/

does not depend on the choice of the integer s. Indeed, using

(1), (2) and (6) we conclude for s C 1 that

.sC1/

D '

.sC1/

BQ'

sC1

.x/

D '

s

B '

1

BQ' BQ'

.x/

D '

s

B '

1

B ' BQ'

.x/

D '

s

BQ'

.x/

D y

.s/

;

where, in view of (1), we have used that Q' BQ'

.x/ D ' BQ'

.x/ if Q'

.x/ 2 Q.

We now deﬁne the map j W E

! R

.Givenx

2 E

, we choose by means

of (3) an integer s  0 so large that Q'

; h.x

// 2 Q and set

j.x

/ ´ '

s

BQ'

; h.x

// 2 W

.0; '/:

According to the above remark, j.x

/ does not depend on the choice of the integer

s, as long as Q'

.x/ 2 Q. We check the properties of this map j .

(i) The equation W

.0; '/ D j.E

/ follows from the statements (2)–(5).

(ii) In order to prove the injectivity of the map j , namely that x

¤ x

implies

j.x

/ ¤ j.x

/, we take two points x

2 E

. Then, there exists, due to (3)

and (6) a large integer s  0 such that simultaneously Q'

; h.x

// 2 Q and

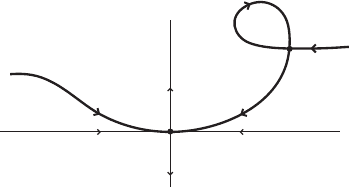
II.3. Stable and unstable invariant manifolds 73



Figure II.10. Does not happen according to the theorem by Smale: W

having a self

intersection.

; h.x

// 2 Q and hence by deﬁnition,

j.x

/ D '

s

BQ'

; h.x

//;

j.x

/ D '

s

BQ'

; h.x

//:

We assume now that j.x

/ D j.x

/. Since '

s

and Q'

are diffeomorphisms,

in particular bijective, it follows that .x

; h.x

// D .x

; h.x

//, and therefore

D x

(iii) It remains to show that dim dj .x

D dim E

for all x

2 E

. With

the injection map j

W E

! R

deﬁned by j

/ ´ .x

; h.x

// we can write

j.x

/ D '

s

BQ'

B j

and conclude by the chain rule for the derivative dj .x

/ 2 L.E

; R

/ that

dj .x

/ D d'

s

. Q'

B j

// B d Q'

// B dj

/;  2 E

Due to dj

/ D .; dh.x

//,

dim dj

D dim E

Since d'

s

.p/, d Q'

.p/ 2 L.R

/ are linear isomorphisms in every point p 2 R

it follows that dim dj .x

D dim E

and the theorem of S. Smale is proved.



In the following we shall abbreviate the stable and unstable invariant manifolds

issuing from the hyperbolic ﬁxed point 0 D '.0/ by simply writing

.0/ Dfx j '

.x/ ! 0; j !1g;



.0/ Dfx j '

j

.x/ ! 0; j !1g:

74 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

We recall that these two immersed manifolds are invariant under the diffeomor-

phism,

'.W

/ D W

;'.W



/ D W



;

contain the ﬁxed point 0 and intersect transversally in 0, so that with the tangent

spaces T

D E

and T



D E



we have

˚ T



D T

The stable and unstable invariant manifolds cannot intersect themselves but they

can intersect each other in points other than the ﬁxed point, namely in so-called

homoclinic points, discovered by H. Poincaré in the restricted 3-body problem of

celestial mechanics.

Deﬁnition. A point of intersection

 2 W



.0/ \ W

.0/ nf0g

is called a homoclinic point (to the ﬁxed point 0).

In view of the invariance of the stable and unstable invariant manifolds the

orbit O./ of such a homoclinic point consists of homoclinic points, and every

homoclinic point converges to the hyperbolic ﬁxed point under the iterates of the

diffeomorphism as well as under the iterates of the inverse diffeomorphism. Hence

the homoclinic orbit converges in forward and backward direction to the ﬁxed point.

./ ! 0; j !C1;

./ ! 0; j !1;

./ 2 W

.0/ \ W



.0/; j 2 Z:

The closure of the homoclinic orbit O./ is the set

ƒ ´

[

j 2Z

./ [f0g:

It consists of two orbits, namely O./ and O.0/ Df0g. The set ƒ is compact and

invariant, '.ƒ/ D ƒ.

Deﬁnition. The homoclinic point  is called transversal (or nondegenerate), if the

manifolds W

.0/ and W



.0/ intersect transversally in , i.e.,



.0/ ˚ T





.0/ D T



Since the immersed manifolds are invariant and cannot intersect themselves,

the transversal homoclinic orbit forces them to oscillate faster and faster as they

approach the hyperbolic ﬁxed point, doubling back and piling up on themselves

as illustrated in Figure II.11 and one expects quite a complicated orbit structure

nearby.

II.3. Stable and unstable invariant manifolds 75



1

./

2

./

.0/



.0/



.0/

Figure II.11. Stable and unstable invariant manifolds possessing a transversal homoclinic

point.

Example. As an illustration we shall describe a simple example of a diffeomor-

phism in the plane exhibiting homoclinic points. An effective way to produce

diffeomorphisms is to take ﬂow maps of vector ﬁelds and so we start with the

differential equation of second order on the real line,

Rx D x  x

D

V.x/;

where the potential function is given by

V.x/ D

This differential equation is equivalent to the system of ﬁrst-order differential

equations









V.x/



μ X.x; y/;

deﬁned by the smooth time independent vector ﬁeld X in the plane. The vector

ﬁeld possesses the integral H W R

! R, deﬁned as the function

H.x;y/ D

C V.x/:

As a consequence, the solution curves of the vector ﬁeld lie on the compact level

sets f.x; y/ 2 R

j H.x;y/ D const.g and hence do exist for all times. The level

sets are illustrated in Figure II.12.

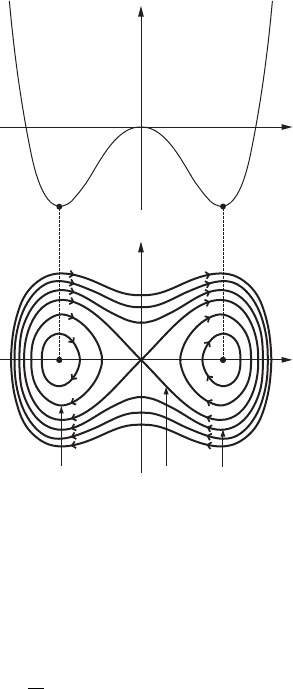
76 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

H D 0

H<0 H>0

V.x/

Figure II.12. The potential V and the level lines of the integral H .

The ﬂow '

of the vector ﬁeld X is deﬁned by the unique solutions of the Cauchy

initial value problem,

.z/ D X.'

.z//; t 2 R;

.z/ D z;

where we have abbreviated the points of the plane by z D .x; y/. Foragiven

point z, the continuously differentiable curve t 7! '

.z/ in the plane is the unique

solution of the vector ﬁeld X passing through the point '

.z/ D z (called the initial

condition) at the time t D 0. For ﬁxed time t D T>0the time T map

z 7! '

.z/

is a diffeomorphism of the plane R

The equilibrium points (or rest points) of the vector ﬁeld are the points z



which the vector ﬁeld vanishes, X.z



/ D 0. In view of the uniqueness of the

Cauchy initial value problem the solution through the rest point is constant, that

is, '



/ D z



for all times t so that the equilibrium point is a ﬁxed point of all

II.3. Stable and unstable invariant manifolds 77

the time T -maps, '



/ D z



. How do we know whether such a ﬁxed point is a

hyperbolic point?

Lemma II.12. Let '

be the ﬂow of the time independent vector ﬁeld

Pz D Y.z/

where Y W R

! R

is of class C

. Then the equilibrium point z



of Y (i.e.,

Y.z



/ D 0) is a hyperbolic ﬁxed point of the time T -map '

of the ﬂow for T>0,

if the linearized vector ﬁeld dY.z



/ at the equilibrium point possesses eigenvalues

whose real part is >0as well as eigenvalues with real part <0, but no eigenvalue

having real part equal to 0.

Proof. Differentiating the Cauchy initial value problem in the space variable at the

equilibrium point z



while keeping the time t ﬁxed, we see that the linearized ﬂow



/ μ ˆ.t/ is the unique solution of the Cauchy initial value problem

ˆ.t/ D dY.'



//ˆ.t/; ˆ.0/ D 1:

Since z



is an equilibrium point, '



/ D z



and hence dY.'



// D dY.z



is time independent, so that the solution is given by the exponential function

ˆ.t/ D d'



/ D e

t:dY.z



For the spectrum we conclude

.d'



// D exp



.t  .d Y.z



///



;

as is readily veriﬁed by looking at the Jordan normal forms of the linear maps.

Hence the result follows if we choose t D T ¤ 0, and the proof is complete. 

Using this lemma one veriﬁes immediately that the origin 0 D .0; 0/ in our

example above is a hyperbolic ﬁxed point of the ﬂow map '

belonging to the

vector ﬁeld X on R

. Looking at the level set containing this ﬁxed point, one sees

that the stable invariant manifold coincides with the unstable invariant manifold, so

that

.0/ D W



.0/ DfH.x;y/ D 0g:

In this example the stable manifold W

.0/ is a compact set in R

and, in view of

Smale’s theorem, an injective immersion of the real line (see Figure II.13). Every

point  2 W

.0/ nf0gDW



.0/ nf0g is a homoclinic point, but clearly not a

transversal one, since



.0/ D T





.0/:

These tangent spaces are spanned by the vector X./ ¤ 0. We observe that, in

general, a diffeomorphism D '

which is the time T -map of a ﬂow generated

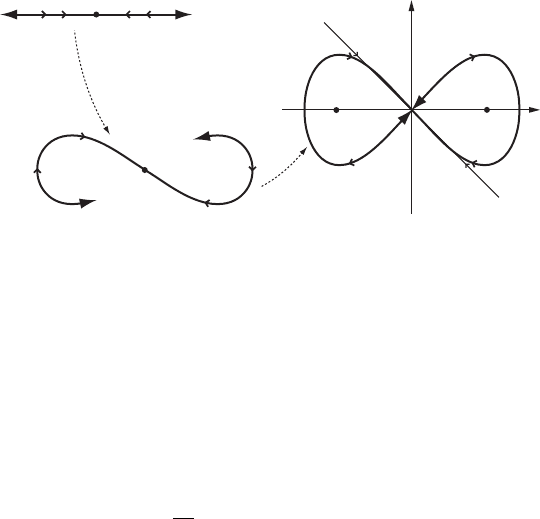
78 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

1

D R

 R

.0; '

/ D j.E

Figure II.13. The injective immersion j in the example.

by a time independent vector ﬁeld, can only admit degenerate homoclinic points.

Indeed, if possesses the hyperbolic ﬁxed point 0 giving rise to the homoclinic

point  2 W

.0/ \ W



.0/ we take the unique solution '

./ passing through the

point  and deﬁned on an open interval containing t D 0. It consists of homoclinic

points, because

.// D '

.// ! '

.0/ D 0 converges to the ﬁxed

point as n !˙1. Consequently,

./

tD0

D X./

is a tangent vector in T



and also in T





and since X./ ¤ 0 we obtain



\ T





¤f0g;

so that the homoclinic point  is not transversal, as claimed.

In order to create transversal homoclinic points we shall take in the next chapter

a time dependent perturbation of our time independent vector ﬁeld X in the plane

and start off from the equation

Rx D x  x

C "f .t; x; Px/;

where f is a smooth function that is periodic in time of period T>0, such that

f.t C T; x; Px/ D f.t;x; Px/ for all t;x; Px. The associated vector ﬁeld X.t; z; "/

is now time periodic and depends on the parameter ". The hyperbolic ﬁxed point



D 0 for " D 0 has a continuation to a hyperbolic ﬁxed point z



."/ of the time

T -ﬂow map '

.z; "/ of the perturbed system, if " ¤ 0 is small. This follows

immediately from the implicit function theorem. Indeed, we consider the smooth

function F W R

 R ! R deﬁned as

F.z;"/ ´ '

.z; "/  z;

II.3. Stable and unstable invariant manifolds 79



.0/



.0/



.0/

Figure II.14. Two possible scenarios after perturbation: transversal homoclinic point  (left)

and W

.0/ \ W



.0/ Df0g (right).

so that F.z;"/ D 0, if and only if '

.z; "/ D z is a ﬁxed point. In order to apply

the implicit function theorem we observe that for " D 0 we have the ﬁxed point

z D 0, so that F .0; 0/ D 0. Denoting by D

the partial derivative in the variable

z, we obtain

F .0; 0/ D D

.0; 0/  1:

If " D 0, the linear map D

.0; 0/ is hyperbolic, as we know, and hence does not

admit an eigenvalue equal to 1. Therefore, D

F .0; 0/ is a linear isomorphism and

the implicit function theorem guarantees a unique differentiable function " ! z



."/

deﬁned for small " and satisfying z



.0/ D 0 and F.z



."/; "/ D '



."// 



."/ D 0. The ﬁxed point z



."/ remains hyperbolic if " is small, since the

eigenvalues of the Jacobi matrix D



."/; "/ depend continuously on ". In the

next chapter, we will see that under additional assumptions on the perturbation these

ﬁxed points z



."/ can give rise to transversal homoclinic points for small " ¤ 0.

Deﬁnition. We assume that x



and y



are two different hyperbolic ﬁxed points of

the diffeomorphism '. A point  is called heteroclinic to x



and y



 2 W



/ \ W





A heteroclinic point  is called transversal if





/ ˚ T







/ D T



The orbit of a heteroclinic point  satisﬁes

./ ! x



;j!C1

and

./ ! y



;j!1

in view of the deﬁnitions of W



/ and W





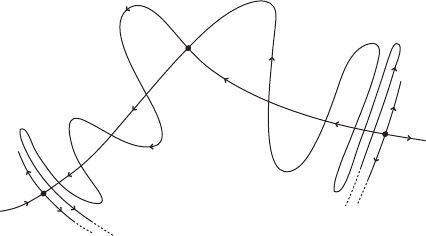
80 Chapter II. Invariant manifolds of hyperbolic ﬁxed points











Figure II.15. Transversal heteroclinic point  associated with the hyperbolic ﬁxed points



and the invariant manifolds.

Literature. The above theorem about local invariant manifolds is named after

J. Hadamard, in view of[47] (1910) and after O. Perron in view of [82] (1928). The

purpose of the paper [29] (1976) by J. J. Duistermaat is to show that “the results of

Perron on perturbed linear systems imply without much effort most of the geometric

results on stable manifolds and hyperbolic sets …”. Proofs of invariant manifolds

can be found in almost all books on dynamical systems and ordinary differential

equations, for example (apart from the references in Chapter I) in the books [53]by

M. Irwin, and [5] by H. Amann. For more recent proofs we refer to M. Chaperon

in [15] and in [16] and the references therein. Our proofs of the invariant mani-

fold theorem and Smale’s theorem make use of the lectures [119] by J. C. Yoccoz.

Homoclinic points were discovered by H. Poincaré in [87] in the restricted 3-body

problem of celestial mechanics. This interesting discovery is described in [6]by

K. Anderson. “Homoclinic trajectories: from Poincaré to the present” is the title of

the article [102] by L. P. Shil’nikov. As for recent existence results of homoclinic

points and further references we refer to [118] by J. Xia. He demonstrates that for

a generic area preserving diffeomorphism on a compact surface, homotopic to the

identity, every hyperbolic ﬁxed point possesses a transversal homoclinic point. On

the other hand, an old result by E. Zehnder [120] shows that generically even an

elliptic ﬁxed point of an area preserving diffeomorphism in two dimensions is a

cluster point of transversal homoclinic points.