Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

I.5. Measure preserving maps and the ergodic theorem 41

Then

fdm 0; for all n  1:

Proof. From the deﬁnition of S

it follows that

f.x/C S

.T x/  f.x/C S

.T x/ D S

kC1

.x/; 0  k  n:

If x 2 A

, then there exists an integer 1  k  n for which S

.x/>0. Conse-

quently,

f.x/C S

.T x/  max

1kn

.x/ D max

0kn

.x/ D S

.x/

and hence f.x/  S

.x/ S

.T x/. By using that S

is equal to zero outside of

and S

.T x/  0 everywhere, we conclude from this inequality and from the

measure preservation of the map T that

f 

.x/ 

.T x/

.x/ 

.T x/



.x/ 

.T x/

.x/ 

.x/

D 0

and the lemma is proved. 

(2) For a<bwe deﬁne the subset Y of X by

Y D Y.a;b/ D

x 2 X j lim

.x/<a<b<lim

.x/

Lemma I.23. The set Y is measurable and invariant under the map T , i.e.,

1

.Y / D Y .

Proof. The statement Y 2 A follows from elementary measure theory, since the

functions S

are all measurable. To prove the invariance, we have to show that

lim

.x/ D lim

.T x/ and lim

.x/ D lim

.T x/: However, this fol-

lows immediately from the identity

.T x/ D

nC1

.x/ 

f.x/ D

n C 1

nC1

.x/

n C 1

„ƒ‚…



f.x/

„ƒ‚…

by taking the lim respectively lim, and the lemma is proved. 

42 Chapter I. Introduction

Lemma I.24. From m.X / < 1 it follows that m.Y / D 0.

Proof. We apply Lemma I.22 to the T -invariant set Y (instead of X) and to the

function g (instead of f ), deﬁned by

g.x/ ´ f.x/ b:

Since m.X / < 1 the function g 2 L.X; A;m/is integrable. Hence, setting

Dfx 2 Y j S

.g;x/>0g;

we have

.f  b/ D



.f  b/  0:

According to the deﬁnition of Y there exists for every point x 2 Y an integer j for

which

.g; x/ D

.f; x/  b>0

and hence S

.g;x/>0. Consequently every x 2 Y is contained in some set A

,so

that Y D

n1

. The monotonicity of the sequence of sets A

 A

nC1



implies lim 

.x/ D 

.x/. Using the convergence theorem of Lebesgue we

obtain in the limit as n !1,

.f  b/  0:

In exactly the same way one proves

.a  f/ 0. Addition of the inequalities

results in the inequality

.a  b/

dm D .a b/m.Y /  0:

Since a<b, one concludes m.Y / D 0 and the lemma is proved. 

(3) Pointwise convergence. In view of Lemma I.24 the set

x 2 X j lim

.x/ < lim

.x/

;

is the countable union of null sets

[

a<b

a;b2Q

Y.a;b/;

and hence a null set, so that m.N

/ D 0: For x … N

, hence for almost all x 2 X,

we abbreviate the limit

lim

.x/ D lim

n!1

.x/ μ '.x/;

I.5. Measure preserving maps and the ergodic theorem 43

where 1  '.x/ C1: Deﬁning '.x/ D 0 on the null set N

we show

next that '.x/ 2 R is a real number almost everywhere. This will follow once

we have proved that ' 2 L.X; A;m/. Since T is measure preserving, we have

jf.T

x/jdm D

jf jdm for every j  0 and therefore,

.x/

dm 

jf jdm:

Using the Lemma of Fatou we can estimate

j'jD

lim

.x/

 lim

.x/



jf j < 1:

Hence ' 2 L.X; A;m/and therefore, '.x/ 2 R almost everywhere. The set

N D N

[fx 2 X jj'.x/jD1g;

on which lim

n!1

.x/ does not exist in R, is therefore a null set. Since the limits

lim

, lim are invariant under T (due to Lemma I.23), the set N is also invariant under

T .Wenowdeﬁne the function f



W X ! R showing up in the statement of the

theorem as follows:



.x/ ´

lim

n!1

.f; x/; x … N;

0; x 2 N:

Then f



2 L.X; A;m/and one sees, as in Lemma I.23, that f



.T x/ D f



.x/ for

all x 2 X. So far, we have proved the statements (i) and (ii) of the ergodic theorem.

(4) It remains to show that

(a)

.f; x/ ! f



in L

(b)



f .

We begin by proving a special case. We assume that f is a bounded function

assuming that jf jK for a constant K>0. Then,

.x/

 K;

and the statement (a) follows by means of the dominated convergence theorem of

Lebesgue. Since the map T is measure preserving,

.x/ D

f; n  1;

and the statement (b) follows, again using the convergence theorem of Lebesgue,

f D lim

n!1

.x/ D

lim

n!1

.x/ D



44 Chapter I. Introduction

(5)We next prove the general case by approximation with the truncated functions

of f 2 L.X; A;m/, deﬁned by

.x/ D

f.x/; jf.x/jN;

0; jf.x/j >N:

Then, jf

jN , and in view of the special case we have the pointwise convergence

;x/ ! f



.x/; n !1

almost everywhere and also the convergence in L

. Let ">0. By the triangle

inequality one estimates

.f /  f



dm 

.f / 

/  f



dmC



 f



jdm;

and we are going to estimate each term on the right-hand side by "=3 if N and n

are sufﬁciently large.

Since f 2 L we have jf j < 1 almost everywhere, and since f

.x/ D

f.x/

jf jN

.x/ ! f.x/ we conclude by the convergence theorem of Lebesgue

that

! f in L

Therefore, choosing N large enough,

 f j"=3:

Using that the map T is measure preserving we can now estimate the ﬁrst term as

follows.

/ 

.f /

dm D

n1

j D0

 f /.T



n1

j D0

j.f

 f /.T

x/jdm

n1

j D0

j.f

 f /.x/jdm

 f jdm

 "=3:

I.5. Measure preserving maps and the ergodic theorem 45

This holds true for all n and the ﬁrst term is taken care of. We now apply the Lemma

of Fatou to the ﬁrst term to obtain as n !1,



 f



jdm  "=3;

which is the desired estimate of the third term. For the second term we conclude

/  f



dm  "=3

for n large enough, from the convergence statement in the special case. Altogether,

.f /  f



 "

for n large enough. This is true for every ">0. Therefore,

.f / ! f



in L

and the proof of the statement (a) in the general case is completed. As for the

statement (b) we recall that, because of the measure preservation of the map T ,

.f / d m D

for all n  1, and using the L

-convergence we ﬁnally obtain

f D lim

n!1

.f / D



Herewith, the ergodic theorem of Birkhoff is proved. 

Literature. There are several monographs on dynamical systems which cover most

of the topics treated in the ﬁrst four chapters. Among them [49] by B. Hasselblatt

and A. Katok, [113] by W. Szlenk, [63] by R. Mañé and [91] by C. Robinson. The

special topic of ergodic theory is treated, for example, in the monographs [23]by

I. Cornﬁeld, S. V. Fomin and Ya. G. Sinai, [108] and [109] by Ya. G. Sinai, [ 88]by

M. Pollicott, [60] by U. Krengel, [37] H. Fuerstenberg and [115] by P. Walters. For

surveys about speciﬁc problems in dynamical systems including historical infor-

mation and many references we recommend the Handbooks of Dynamical Systems

[50] and [35].

Chapter II

Invariant manifolds of hyperbolic ﬁxed points

In this chapter we shall study a diffeomorphism ' W R

! R

of class C

for k  1,

near a ﬁxed point which, by translation, can be assumed to be the origin so that

'.0/ D 0. The orbit through the origin is the set O.0/ Df0g consisting of the

origin. The diffeomorphism ' is of the form

'.x/ D '.0/ C d'.0/x CO'.x/

D d'.0/x CO'.x/

D Ax CO'.x/;

where A 2 L.R

/ is a linear isomorphism and where the remainder satisﬁes

O'.0/ D 0 and d O'.0/ D 0. We shall assume in the following that the ﬁxed point

is hyperbolic. From a dynamical point of view such a ﬁxed point is completely

unstable and we shall ﬁrst demonstrate that near such a ﬁxed point, the orbits of

the diffeomorphism behave topologically like the orbits of the linearized map at the

ﬁxed point (theorem of Hartman–Grobman). There exist two distinguished sets,

called the stable, respectively the unstable invariant manifold, issuing from the hy-

perbolic ﬁxed point. The stable manifold consists of the set of all points in the space

that under the iterates of the map converge to the ﬁxed point, while the unstable

manifold is the set of points that converge under the iterates of the inverse map to the

ﬁxed point. Considering only those points of these sets that stay under the iterates

of the map, respectively under the iterates of the inverse map in the neighborhood

of the ﬁxed point, we shall show that the stable and unstable invariant manifolds

are, locally near the ﬁxed point, embedded submanifolds represented by graphs

of functions (theorem of Hadamard–Perron). Globally, however, these stable and

unstable invariant manifolds are the images of injective immersions of Euclidean

spaces (theorem of S. Smale) which away from the ﬁxed point can intersect each

other, giving rise to so-called homoclinic points. Homoclinic points considerably

complicate the orbit structure of the diffeomorphism nearby and imply the exis-

tence of orbits with quite unpredictable long-time behavior, as the next chapter

will show.

In the following we shall denote by L.X; Y / the vector space of the linear

and continuous maps between the two normed spaces X and Y and abbreviate

L.X/ D L.X; X/.

II.1. Hyperbolic ﬁxed points 47

II.1 Hyperbolic ﬁxed points

We shall give two equivalent deﬁnitions of a hyperbolic ﬁxed point.

Deﬁnition. A linear isomorphism A 2 L.R

/ of R

is called hyperbolic, if it leaves

a splitting

D E

˚ E



invariant so that

A D







with respect to E

˚ E



where E

¤f0g and A

2 L.E

/ and A



2 L.E



/. These linear maps satisfy

the inequalities

xjc#

jxj for all j  0; x 2 E

;

j



xjc#



jxj for all j  0; x 2 E



;

with a constant c  0 and with constants

0<#

<1;

0<#



<1:

The ﬁxed point 0 of the above diffeomorphism ' W R

! R

is called hyperbolic

if the linearization of the diffeomorphism at the ﬁxed point A ´ d'.0/ 2 L.R

is a hyperbolic isomorphism.

It is easily veriﬁed that the dynamical behavior of the hyperbolic map A char-

acterizes the spaces E

and E



as follows:

Dfx 2 R

j A

x ! 0; j ! C1g

Dfx 2 R

j sup

j 0

xj < 1g;



Dfx 2 R

j A

x ! 0; j ! 1g

Dfx 2 R

j sup

j 0

j

xj < 1g:

We shall use the following notation with respect to the splitting R

D E

˚E



x D .x



/ D x

˚ x



;

Ax D .A



/ D A

˚ A



An alternative deﬁnition of the hyperbolicity of an isomorphism A in terms of

its spectrum .A/ consisting of the set of eigenvalues of A is the following.

48 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

Deﬁnition. An isomorphism A 2 L.R

/ is called hyperbolic if its spectrum has

the properties

jj¤1;  2 .A/;

and there exist points  in the spectrum satisfying jj <1and also points satisfying

jj >1.

Figure II.1. Spectrum of a hyperbolic isomorphism.

The two deﬁnitions of a hyperbolic linear isomorphism are equivalent. Indeed, if

A is hyperbolic according to the second deﬁnition, we denote by E

the generalized

eigenspace of all eigenvalues  satisfying jj <1and by E



the generalized

eigenspace of all eigenvalues with jj >1and obtain the invariant splitting R

˚ E



The restricted maps A

D Aj

W E

! E

(and analogously for A



)have

the spectra

.A

/ D .A/ \fjzj <1g;

.A



/ D .A/ \fjzj >1g:

In order to verify the desired estimates for jA

xj and jA

j



xj on E

and E



we recall that the spectral radius r

´ maxfjjj 2 .A

/g of A

satisﬁes

lim

j !1

D r

<1;

where kkdenotes the operator norm. Therefore, we ﬁnd an integer j

such that

for all j  j

the estimates kA

 # hold true for a constant #<1and the

inequalities jA

xj#

jxj follow from the deﬁnition of the operator norm. To

ensure the desired estimate also for the ﬁnitely many j<j

, one simply puts a

sufﬁciently large constant c in front of the previous estimates on the right-hand side.

The estimates for jA

j



xj follow by the same argument applied to the linear map

1



. Therefore, the two deﬁnitions of hyperbolicity are equivalent.

II.1. Hyperbolic ﬁxed points 49

Example. The linear map A 2 L.R

/, in the canonical basis fe

g represented

by the matrix

A D



0

0



; 0<<1<;

has the spectrum .A/ Df; g. Moreover, E

D R f0g and E



Df0gR.

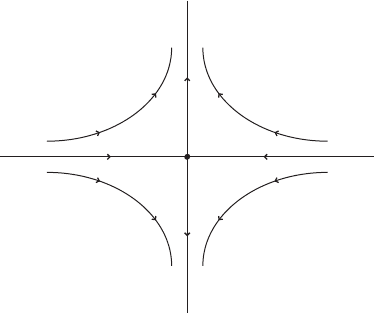
The orbits are sketched in Figure II.2.



Figure II.2. Schematic representation of the orbits of A 2 L.R

/ in the example.

It is convenient for the arguments later on to introduce new and equivalent norms

with respect to which the constant c in the deﬁnition of the hyperbolicity is equal

to 1.

Proposition II.1 (Adapted norms). Assume that the map A 2 L.R

/ is hyperbolic.

Then, there exist equivalent norms jj



on E

and E



such that



 ˛jxj



;x2 E

;

1





 ˇjxj



;x2 E



;

with constants #

<˛<1and #



<ˇ<1.

With respect to these norms the linear maps A

and A

1



are contractions, so

that kA



<1and kA

1





<1.

Proof. In order to construct the new norm in the space E

we choose #

<˛<1

and then choose the integer N so large that

c.#

=˛/

 1:

50 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

For x 2 E

we deﬁne the new norm on E

jxj



N 1

j D0

j

xj:

It satisﬁes

jxjjxj



 C jxj

with the constant C D cN, so that the two norms are equivalent. It remains to

verify that A

is a contraction satisfying kA



 ˛<1. To see this, we estimate



N 1

j D0

j

j C1

D ˛



N 1

j D1

j

xjC˛

N



 ˛



N 1

j D1

j

xjCjxj



D ˛

N 1

j D0

j

D ˛jxj



;

where we have used, in view of our choice of the integer N , that

N

xjc˛

N

jxjjxj:

On the subspace E



one carries out the same construction taking A

1



instead

of A

. The proposition is proved. 

As already mentioned at the beginning of the chapter, a hyperbolic ﬁxed point

gives rise to the so-called stable manifold and the unstable manifold. The stable

manifold consists of all the points in the space that converge under the iterates of

the map to the ﬁxed point, while the unstable manifold consists of all those points

that converge to the ﬁxed point under the iterates of the inverse map.

Deﬁnition. The stable, respectively unstable, invariant manifold of a hyperbolic

ﬁxed point x



of the diffeomorphism ' are the sets

.'; x



/ ´fx 2 R

j '

.x/ ! x



;j!1g;



.'; x



/ ´fx 2 R

j '

j

.x/ ! x



;j!1g: