Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities

Подождите немного. Документ загружается.

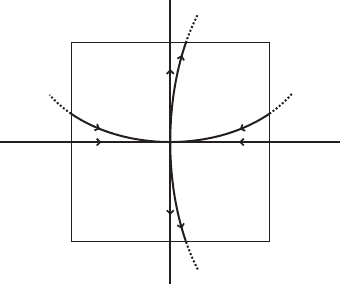
II.1. Hyperbolic ﬁxed points 51



D T





D E



.'; x





.'; x



Figure II.3. Hyperbolic ﬁxed point x



with W

.'; x



/ and W



.'; x



/ in a neighborhood Q.

These sets contain the ﬁxed point x



and are clearly invariant under the map,

'.W

/ D W

;

'.W



/ D W



Example. If x



D 0 and ' D A 2 L.R

/ is a hyperbolic linear isomorphism, then

.A; 0/ D E



.A; 0/ D E



This is the dynamical characterization of the spaces E

and E



In order to study the topological behavior of a diffeomorphism locally near the

hyperbolic ﬁxed point we start with a technical preparation.

Proposition II.2. If X is a Banach space and A 2 L.X; X / a linear isomorphism

and ' W X ! X a map of the form

'.x/ D Ax C g.x/;

where g W X ! X is a Lipschitz-continuous map whose Lipschitz constant " satisﬁes

"kA

1

k <1;

then the map ' is a homeomorphism of X and the inverse map '

1

is Lipschitz-

continuous.

Proof. (1) We ﬁrst prove that the map ' is bijective. Let y 2 X . Since A is

bijective, there exists a unique x

2 X solving Ax

D y and we show that there

52 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

exists a unique solution x 2 X of the equation y D Ax

D Ax C g.x/, and hence

solving the equation

x D x

 A

1

g.x/:

Deﬁning f W X ! X by f.x/ ´ x

 A

1

g.x/ it follows from the assumptions

of the proposition that

jf.x/ f.y/jDjA

1

g.x/  A

1

g.y/jkA

1

k"jx  yj;

so that f is a contraction. The contraction principle guarantees a unique ﬁxed

point x D f.x/ D x

 A

1

g.x/. This ﬁxed point x is the unique solution of the

equation y D '.x/ and we see that ' is bijective.

(2) Next we shall verify the Lipschitz continuity of the inverse. From jx yjD

1

Ax  A

1

Ay jkA

1

kjAx  Ay j we conclude

jAx  Ay jkA

1

jx  yj;

and so, using the triangle inequality, we can estimate

j'.x/  '.y/jDjAx  Ay C g.x/  g.y/j

jAx  Ay jjg.x/  g.y/j

 .kA

1

 "/jx  yj:

Using our assumption "<kA

1

, one obtains

jx  yj

j'.x/  '.y/j

1

 "

and therefore,

1

.u/  '

1

.v/j

ju  vj

1

 "

for all u; v 2 X. We see that the inverse map '

1

is Lipschitz-continuous with

Lipschitz constant equal to

1

1

 "

1

1  "kA

1

;

and the proposition is proved. 

Our next result describes the local behavior of a diffeomorphism ' near a

hyperbolic ﬁxed point. The diffeomorphism behaves in an open neighborhood of

the ﬁxed point topologically like the linearized map at the ﬁxed point.

II.1. Hyperbolic ﬁxed points 53

Theorem II.3 (Hartman–Grobman). Let 0 be a hyperbolic ﬁxed point of the dif-

feomorphism ' W R

! R

so that

'.x/ D Ax CO'.x/;

O'.x/

jxj

! 0; x ! 0;

with a linear hyperbolic isomorphism A. Then, there exist open neighborhoods U

and V of 0 and a homeomorphism h W U ! V satisfying h.0/ D 0 and

h B '.x/ D A B h.x/

if x 2 U and '.x/ 2 U . Consequently, if deﬁned,

h B '

B h

1

.y/ D A

y; j 2 Z:

The proof of this local theorem is based on the following global perturbation

theorem of a hyperbolic map A 2 L.R

Theorem II.4. Let A 2 L.R

/ be a hyperbolic isomorphism and let ', W R

be two mappings of the form

'.x/ D Ax CO'.x/; .x/ D Ax C

.x/

where the mappings O' and

are bounded and Lipschitz-continuous,

jO'j

´ sup

x2R

jO'.x/j < 1;

jO'.x/ O'.y/j"jx  yj for all x; y 2 R

;

and the same for the map

with the same Lipschitz constant ". Then, if " is

sufﬁciently small, the maps ' and are homeomorphisms of R

and there exists a

unique homeomorphism hW R

! R

of the form

h.x/ D x C

h.x/; j

< 1



Figure II.4. The theorem by Hartman and Grobman.

54 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

satisfying

' B h.x/ D h B .x/; x 2 R

Moreover, h.0/ D 0 if we assume, in addition, that '.0/ D 0 D .0/.

Proof [Contraction principle]. According to Proposition II.2, the maps ' and are

homeomorphisms for small ". Moreover, they are Lipschitz-continuous and their

inverse maps are also Lipschitz-continuous.

If ' D A CO' and D A C

are the two given maps, we look for a mapping

u D Id COu, which solves the functional equation ' Bu D u B or, more explicitly,

the equivalent equation

A C A Ou CO' B u D A C

COu B :

Hence, we ﬁrst look for a continuous and bounded map OuW R

! R

that solves

the functional equation

A Ou.x/ Ou. .x// D

.x/ O'.u.x//; x 2 R

We denote by X ´ C

; R

/ the Banach space of continuous and bounded

mappings v W R

! R

, equipped with the sup-norm

jvj

D sup

x2R

jv.x/j;

where in R

we choose for x D .x



/ 2 E

˚ E



the maximum norm jxjD

maxfjx

j; jx



jg. The norms jx

j, jx



j are the adapted norms on E

and E



introduced in Proposition II.1.

We now introduce the linear and continuous map L 2 L.X/ as follows:

LW X ! X; v 7! Lv;

.Lv/.x/ ´ Av.x/  v. .x//; x 2 R

;

or in short,

Lv D Av  v B :

Lemma II.5. If A 2 L.R

/ is a hyperbolic isomorphism, then the map L W X ! X

is also a continuous linear isomorphism of the Banach space and so the inverse

map has a ﬁnite operator norm kL

1

k < 1.If .0/ D 0, it follows for v 2 X

satisfying v.0/ D 0 that also .L

1

v/.0/ D 0.

Proof [Hyperbolicity of A]. Foragiveng 2 X we look for a solution v 2 X of

the equation

Av  v B D g:

According to the splitting R

D E

˚ E



, we decompose the hyperbolic isomor-

phism A D A

˚ A



satisfying, with respect to the adapted norms, the estimates

k#; kA

1



k#; 0<#<1:

II.1. Hyperbolic ﬁxed points 55

Decomposing the images, we set

v.x/ D v

.x/ ˚ v



.x/;

g.x/ D g

.x/ ˚ g



.x/;

for functions v

W R

! E

and v



W R

! E



which are elements of the Banach

spaces X

D C

/. We wish to solve the system of equations

 v

B D g

;



 v



B D g



Rewriting these equations by composing the ﬁrst equation from the right with B

1

and applying the linear map A

1



B from the left to the second equation we obtain

the equivalent system

 A

1

Dg

1

;



 A

1



B D A

1



Introducing the linear operators G

2 L.X

/ by

/.x/ ´ A

1

.x//;



/.x/ ´ A

1



. .x//;

we can rewrite the previous equations in X

.1  G

Dg

1

;

.1  G



D A

1



From the hyperbolicity of the isomorphism A we deduce the following estimates

in the sup-norm:

kA

kjv

 #jv

;



kA

1



kjv



 #jv



For the operator norms we therefore obtain the estimates kG



k, kG

k#<1.

Thus the inverse maps are given by the well-known Neumann series, namely

.1  G

1

j 0

2 L.X

Therefore the desired unique solution v, given by

D .1  G

1

.g

1

//;



D .1  G



1



56 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

satisﬁes the estimates in the sup-norm:



1  #

;





1  #





1  #



We have solved the equation Lv D g in the Banach space X for a unique v. From

1

=jgj

Djvj

=jgj

 1=.1  #/ for every 0 ¤ g 2 X we conclude

that the operator norm of the inverse map satisﬁes kL

1

k1=.1  #/ < 1. The

proof of the lemma is complete. 

It is instructive to look at the explicit formulas for the inverse maps v

1

/. They are as follows:

.x/ D

j 0

.j C1/

.x//;



.x/ D

j 0

.j C1/



.x//:

Coming back to the proof of Theorem II.4, we want to solve the functional

equation A Ou.x/ Ou. .x// D

.x/ O'.u.x//. The left-hand side of the equation

is equal to L Ou (x), and we have to solve the equation

Ou D L

1

O' B .Id COu/ μ F.Ou/;

where, on the right-hand side, we also have deﬁned the map F W X ! X , which is

a contraction if " is small enough. Indeed,

F.Ou/  F.Ov/ DL

1

Œ O' B .Id COu/ O' B .Id COv/;

and according to the Lipschitz assumption in Theorem II.4,

jO'.x COu.x// O'.x COv.x//j"jOu.x/ Ov.x/j"jOu Ovj

;

so that

jO' B .Id COu/ O' B .Id COv/j

 "jOu Ovj

Hence, in view of Lemma II.5,

jF.Ou/  F.Ov/j

kL

1

k"jOu Ovj

< 1

for all Ou, Ov 2 X. Choosing " small enough, the map F W X ! X is a contraction.

Consequently, there exists a unique ﬁxed point

h of F , and the map h ´ Id C

is the unique solution of the functional equation from Theorem II.4 in the class of

the maps hW R

! R

satisfying h  Id 2 X.

II.1. Hyperbolic ﬁxed points 57

It remains to show that h D Id C

h is a homeomorphism. We shall conclude

this from the uniqueness of the solution of the functional equation ' B h D h B .

If we exchange ' and , there exists again a unique map g D Id COg satisfying

jOgj

< 1 and solving the functional equation B g D g B '. We then get

' B .h B g/ D h B B g;

h B B g D .h B g/ B ';

and therefore, ' B .h B g/ D .h B g/ B '. On the other hand, ' B Id D Id B'. Since

h B g D Id Cw satisﬁes jwj

< 1, it follows from the uniqueness of the solution

of the functional equations in this class that h B g D Id. In exactly the same way,

one sees that also g B h D Id. Since the inverse map h

1

D g is continuous, the

map hW R

! R

is a homeomorphism. The proof of Theorem II.4 is complete.



Lemma II.6. Let X be a Banach space and B

the closed ball in X centered at 0

and of radius r. Then the map f W X ! B

deﬁned by

f.x/ D

x; jxjr;

jxj

; jxjr

is Lipschitz-continuous with a Lipschitz constant equal to 2.

Proof. Let x; y 2 X.Forx; y 2 B

the statement is obvious. Assuming that

jxj; jyj >rwe estimate, using the triangle inequality,

jf.x/ f.y/jDr

jxj



jyj

jxj

x 

jxj

jyj



jxj



jx  yjC

y 

jxj

jyj



jxj



jx  yjC

jyjjxj





jxj

.jx  yjCjx  yj/

 2jx  yj:

The remaining cases are veriﬁed similarly. 

After these preparations, we shall prove the Hartman–Grobman theorem.

Proof of Theorem II.3. We consider the diffeomorphism

'.x/ D Ax CO'.x/

58 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

of Theorem II.3 possessing the origin as a hyperbolic ﬁxed point. Fix ı>0and

let B

be the closed ball centered at 0 with radius r. According to the assumption,

O'.0/ D 0 and O'

.0/ D 0, where O'

denotes the derivative d O'. Since O'

is continuous,

we can choose the radius r D r.ı/>0so small that jO'

.x/j <ıon B

. Then, the

map O' is Lipschitz-continuous on B

and has a Lipschitz constant <ı.Wenow

modify the given diffeomorphism outside of B

in such a way that the modiﬁed

map meets the assumptions of the technical Theorem II.4. For this purpose, we

take the map f introduced in Lemma II.6 and deﬁne the map ˆ by

ˆ.x/ ´ Ax C

ˆ.x/ ´ Ax CO'.f .x//; x 2 R

Thus, ˆ D ' on B

and

ˆ is, according to the above lemma, Lipschitz-continuous

with a Lipschitz constant <2ı. Since O' is bounded on B

, we also have j

ˆj

< 1.

Finally we can apply Theorem II.4 (in this theorem we take A instead of ' and

ˆ instead of ). If ">0is the smallness constant occurring in Theorem II.4,we

choose ı>0so small that 2ı < ". Then Theorem II.4 guarantees a homeomor-

phism h satisfying h.0/ D 0 and solving the functional equation h Bˆ D A Bh.By

choosing U  B

and introducing V ´ h.U / and restricting h on U , we conclude

that h B' D A Bh on U \ '

1

.U /, as claimed in the theorem. This completes the

proof of the theorem of Hartman–Grobman. 

II.2 Local invariant manifolds

Having looked at the behavior of orbits near the unstable ﬁxed point from a topo-

logical point of view, we shall look at it next from a differentiable point of view and

come back to the diffeomorphism ' W R

! R

of class C

, for k  1 possessing

the hyperbolic ﬁxed point 0 D '.0/, so that it is of the form

'.x/ D Ax C g.x/;

where g is a function satisfying g.0/ D 0, g

.0/ D 0 and where A 2 L.R

/ is the

linearized map having the representation

A D







with respect to E

˚ E



D R

and satisfying kA

k˛ and kA

1



k˛ for a constant 0<˛<1.

Deﬁnition. For the neighborhood Q of the ﬁxed point 0, deﬁned by

Q ´fx D .x



/ 2 E

˚ E



jjx

jr; jx



jrg;

r>0, the local invariant manifolds of the ﬁxed point 0 are deﬁned as the sets

loc

.Q/ ´fx 2 Q j '

.x/ 2 Q for all j  0g;



loc

.Q/ ´fx 2 Q j '

j

.x/ 2 Q for all j  0g:

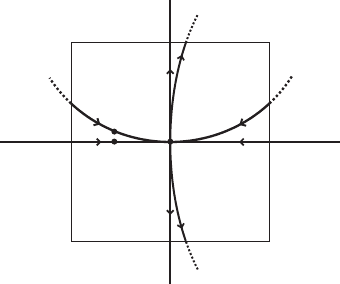
II.2. Local invariant manifolds 59

These sets are clearly invariant under ' resp. '

1

'.W

loc

/  W

loc

1



loc

/  W



loc

It turns out that these distinguished sets consist of those points in Q which do

converge under the iterates of the map, resp. under the iterates of the inverse map to

the ﬁxed point. Moreover, the sets are embedded manifolds represented by graphs

of differentiable functions.

Theorem II.7 (Hadamard–Perron). We assume that the diffeomorphism ' belongs

to the differentiability class C

for some k  1. Then if r>0is sufﬁciently small,

loc

.Q/ Dfx 2 Q j '

.x/ 2 Q; j  0 and '

.x/ ! 0; j !1g

Dfx 2 Q j x D .x

; h.x

// 2 E

˚ E



where h W E

! E



is a function of class C

satisfying h.0/ D 0 and h

.0/ D 0,

so that the tangent space at the point 0 is given by

loc

.Q/ D E

x D .x

; h.x



loc

.Q/



loc

.Q/

Figure II.5. The theorem of Hadamard and Perron.

Similarly,



loc

.Q/ Dfx 2 Q j '

j

.x/ 2 Q; j  0 and '

j

.x/ ! 0; j !1g

Dfx 2 Q j x D .k.x



/; x



/ 2 E

˚ E



with a function k W E



! E

from C

satisfying k.0/ D 0 and k

.0/ D 0, so that



loc

.Q/ D E



60 Chapter II. Invariant manifolds of hyperbolic ﬁxed points

The theorem of Hadamard–Perron is of local nature but will be deduced from a

global perturbation theorem of the linear map A. To do so we assume, in addition,

that the map '.x/ D Ax C g.x/ satisﬁes

jgj

< 1; jg

 ı;

so that g can be considered as a small perturbation of the linear map A 2 L.R

The locally stable and unstable manifolds of this map are now deﬁned as the sets

loc

/ Dfx 2 R

j sup

j 0

.x/j < 1g;



loc

/ Dfx 2 R

j sup

j 0

j

.x/j < 1g:

The sets consist of bounded half orbits of the map ' and we are going to prove that

these half orbits converge under the iterates of the map, resp. under the iterates of

the inverse map to the hyperbolic ﬁxed point. We shall also see that these sets are

embedded submanifolds.

Theorem II.8. Let ' W R

! R

be a C

-diffeomorphism (k  1) possessing the

hyperbolic ﬁxed point x D 0 and let ' be of the form '.x/ D Ax C g.x/ with a

map satisfying g.0/ D 0, jgj

< 1 and jg

 ı. Then, if ı is small enough,

loc

/ Dfx 2 R

j '

.x/ ! 0; j !1g

Dfx D .x



/ j x



D h.x

for a function h W E

! E



from C

satisfying h.0/ D 0 and h

.0/ D 0, so that

loc

D E

is the tangent space at the ﬁxed point. Similarly,



loc

/ Dfx 2 R

j '

j

.x/ ! 0; j !1g

Dfx D .x



/ j x

D k.x



for a function k W E



! E

from C

satisfying k.0/ D 0 and k

.0/ D 0 and



loc

D E



Proof [Contraction principle, implicit function theorem]. (1)We ﬁrst show that for

every a D x

2 E

there exists a unique point x

2 R

of the form

D a ˚ h.a/ 2 E

˚ E



;

whose orbit converges to the ﬁxed point, i.e., '

/ ! 0 as j !1.