Zehnder E. Lectures on Dynamical Systems: Hamiltonian Vector Fields and Symplectic Capacities
Подождите немного. Документ загружается.

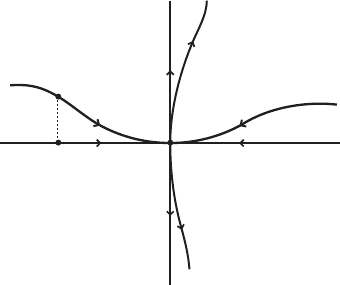
II.2. Local invariant manifolds 61
0
x
C
.x
C
; h.x
C
//
E
C
E
W
C
loc
.R
n
/
W
loc
.R
n
/
Figure II.6. Theorem II.8: W
C
loc
.R
n
/ as graph of h.
We denote in the following by P
˙
2 L.R
n
/ the projections onto E
˙
, defined
by
P
˙
.x
C
;x
/ D x
˙
for .x
C
;x
/ 2 E
C
˚ E
:
According to the postulated A-invariance of the splitting,
AP
˙
D P
˙
A D P
˙
AP
˙
D A
˙
P
˙
:
Moreover, the estimates
kAP
C
k˛; kA
1
P
k˛
hold true for a constant ˛<1.
The sequence .x
j
/
j 0
is a half orbit of the map ',ifx
j C1
D '.x
j
/ for every
j 0, or explicitly, if
x
j C1
D Ax
j
C g.x
j
/; j 0:
We shall next derive successively equivalent but more convenient conditions for a
sequence to be a half orbit of '. In the first step (a) we use the splitting x
j C1
D
P
C
x
j C1
C P
x
j C1
, in order to get two equations. Then we use in step (b) the
commutativity relation P
˙
A D AP
˙
. Then in step (c) we apply A
1
to the second
equation and, finally, in step (d) we use x
j
D P
C
x
j
C P
x
j
and an index-shift to
62 Chapter II. Invariant manifolds of hyperbolic fixed points
come back to a single equation.
x
j C1
D Ax
j
C g.x
j
/
.a/
()
´
P
C
x
j C1
D P
C
Ax
j
C P
C
g.x
j
/;
P
x
j C1
D P
Ax
j
C P
g.x
j
/;
.b/
()
´
P
C
x
j C1
D AP
C
x
j
C P
C
g.x
j
/;
P
x
j C1
D AP
x
j
C P
g.x
j
/;
.c/
()
´
P
C
x
j C1
D AP
C
x
j
C P
C
g.x
j
/;
P
x
j
D A
1
P
x
j C1
A
1
P
g.x
j
/;
.d/
()
8
ˆ
<
ˆ
:
x
j
D AP
C
x
j 1
C P
C
g.x
j 1
/;
CA
1
P
x
j C1
A
1
P
g.x
j
/; j 1;
x
0
D P
C
x
0
C A
1
P
x
1
A
1
P
g.x
0
/; j D 0:
In order to reformulate the last representation of a half orbit as a fixed point of
a functional in a sequence space, we introduce the Banach space X of the bounded
half sequences in R
n
,
X ´fx D .x
j
/
j 0
;x
j
2 R
n
j sup
j 0
jx
j
j < 1g
equipped with the norm
kxk´sup
j 0
jx
j
j:
The norm of the point x
j
D x
C
j
˚ x
j
2 E
C
˚ E
D R
n
is the maximum norm
jx
j
jDmaxfjx
C
j
j; jx
j
jg;
where jx
C
j
j, jx
j
j are the adapted norms on E
C
and E
guaranteed by Proposi-
tion II.1. We shall characterize the bounded half orbits as fixed points of maps. For
this purpose, we introduce the following family of maps. For every a 2 E
C
we
define the map F
a
by
F
a
W X ! X; x D .x
j
/
j 0
7! F
a
.x/ D .F
a
.x/
j
/
j 0
;
where the bounded sequence .F
a
.x/
j
/
j 0
is defined by the formula
F
a
.x/
j
D
´
AP
C
x
j 1
C P
C
g.x
j 1
/ C A
1
P
x
j C1
A
1
P
g.x
j
/; j 1;
a C A
1
P
x
1
A
1
P
g.x
0
/; j D 0:
In view of the above characterization (d) of a half orbit we conclude for the sequence
x D .x
j
/
j 0
2 X that
F
a
.x/ D x ()
´
x
j C1
D Ax
j
C g.x
j
/; j 0;
P
C
x
0
D a:
II.2. Local invariant manifolds 63
We see that the fixed points of F
a
are the bounded half orbits satisfying P
C
x
0
D a.
In order to achieve convergence of the half sequence, we introduce weighted
norms.For 1 we define the subspace X
X by
X
´fx 2 X jkxk
´ sup
j 0
j
jx
j
j < 1g:
If x 2 X
, then
j
jx
j
jkxk
in view of the definition of the norm. Therefore,
jx
j
j
j
kxk
. Hence if we choose >1, it follows that x
j
! 0 as j !1.In
the following we shall choose, recalling that kA
C
k; kA
1
k˛<1, the parameter
in the interval
1 < 1=˛:
Lemma II.9. Every map F
a
maps the space X
into itself,
F
a
W X
! X
;
and satisfies the estimates
kF
a
.x/ F
a
.y/k
.˛ Cı/kx yk
for all x; y 2 X
.
Proof. Let x;y 2 X
. For every j 1 we have
j
ŒF
a
.x/
j
F
a
.y/
j
D
j
AP
C
.x
j 1
y
j 1
/ C
j
P
C
Œg.x
j 1
/ g.y
j 1
/
C
j
A
1
P
.x
j 1
y
j 1
/
j
A
1
P
Œg.x
j
/ g.y
j
/
2 E
C
˚ E
;
while if j D 0, then
F
a
.x/
0
F
a
.y/
0
D A
1
P
.x
1
y
1
/ A
1
P
Œg.x
0
/ g.y
0
/:
We estimate in the max-norm jxjDmaxfjx
C
j; jx
jg for x D .x
C
;x
/. Then,
the operator norms of the projections are equal to 1, kP
C
kD1 and kP
kD1.
According to the assumption of the theorem, jg
0
j
1
ı, and it follows by the mean
value theorem that
jg./ g./jıj j
for all ; 2 R
n
. Therefore, we obtain for the E
C
part of
j
ŒF
a
.x/
j
F
a
.y/
j
if
j 1, using the (a-priori estimates) of the linear map A,
j
jP
C
F
a
.x/
j
P
C
F
a
.y/
j
jkAP
C
k
j 1
jx
j 1
y
j 1
j
C ı
j 1
jx
j 1
y
j 1
j
.˛ Cı/ sup
j 0
j
jx
j
y
j
j
D .˛ Cı/kx yk
:
64 Chapter II. Invariant manifolds of hyperbolic fixed points
Similarly, we find for the E
part the estimates
j
jP
F
a
.x/
j
P
F
a
.y/
j
j.˛ C ı/kx yk
:
For j D 0 the same estimate holds true, in view of the following computation:
jF
a
.x/
0
F
a
.y/
0
jDjA
1
P
.x
1
y
1
/ A
1
P
Œg.x
0
/ g.y
0
/j
˛jx
1
y
1
jC˛ıjx
0
y
0
j
˛jx
1
y
1
jC˛ıjx
0
y
0
j
.˛ C˛ı/kx yk
.˛ Cı/kx yk
.˛ Cı/kx yk
:
Altogether,
j
jF
a
.x/
j
F
a
.y/
j
jDmax
˚
j
jP
C
F
a
.x/
j
P
C
F
a
.y/
j
j;
j
jP
F
a
.x/
j
P
F
a
.y/
j
j
.˛ Cı/kx yk
for every j 0. Consequently, taking on the left-hand side the supremum over
j 0, we have proved the desired inequality
kF
a
.x/ F
a
.y/k
.˛ Cı/kx yk
:
The statement F
a
.X
/ X
follows from this inequality. Indeed, in view of
F
a
.0/ D .a;0;0;:::/we can estimate
kF
a
.x/k
DkF
a
.x/ F
a
.0/ C .a;0;0;:::/k
kF
a
.x/ F
a
.0/k
Ck.a;0;0;:::/k
.˛ Cı/kxk
Cjaj
< 1:
This finishes the proof of Lemma II.9.
Continuing with the proof of Theorem II.8, we recall that 0<˛<1and choose
the smallness parameter ı>0occurring in this theorem, so small that
˛ C ı μ <1
for all parameter values 1 which are contained in the closed interval whose
upper bound is strictly larger than 1 and whose lower bound is equal to 1. For these
parameter values the maps F
a
W X
! X
are contractions in view of Lemma II.9

II.2. Local invariant manifolds 65
so that we can apply the contraction principle. Because of X
X, there exists a
unique fixed point x.a/ D .x.a/
j
/
j 0
2 X satisfying
F
a
.x.a// D x.a/
and belonging to all these spaces X
.
We have proved so far that there exists a unique bounded half orbit satisfying
P
C
x
0
D a. Since x.a/ lies in a space X
with >1, this half orbit converges
automatically to the fixed point 0 of the map '.
The zero component of our fixed point sequence satisfies
x.a/
0
D P
C
x.a/
0
˚ P
x.a/
0
D a ˚ h.a/ 2 E
C
˚ E
D R
n
;
where the map h W E
C
! E
is defined by
h.a/ ´ P
x.a/
0
:
In view of our construction, the half orbit is the sequence
x.a/
j
D '
j
.x.a/
0
/; j 0:
In the case that a D 0 we already have a fixed point of F
0
. Indeed, in view
of g.0/ D 0 the zero sequence 0 D .0/
j 0
is a fixed point. Therefore, by the
uniqueness, x.0/
0
D .0; 0/ 2 E
C
˚ E
and hence h.0/ D 0.
(2) Lipschitz continuity of h. If x.a/ and x.b/ are the two fixed points of the
maps F
a
and F
b
we obtain, using Lemma II.9, the estimate
kx.a/ x.b/k
DkF
a
.x.a// F
b
.x.b//k
kF
a
.x.a// F
a
.x.b//k
CkF
a
.x.b// F
b
.x.b//k
kx.a/ x.b/k
Cja bj:
We therefore conclude kx.a/ x.b/k
1
1
ja bj, and hence, recalling the
definition of the norm in the sequence space, jx.a/
j
x.b/
j
j
j
1
ja bj for
every j 0. In particular, the following estimate holds true for j D 0:
jx.a/
0
x.b/
0
j
1
1
ja bj:
Consequently, recalling h.a/ ´ P
x.a/
0
,
jh.a/ h.b/j
1
1
ja bj
for all a; b 2 E
C
, so that the function h W E
C
! E
is Lipschitz-continuous.

66 Chapter II. Invariant manifolds of hyperbolic fixed points
So far we have proved that the stable invariant manifold is the graph of a
Lipschitz-continuous function and that, moreover, the half orbits of all its points
converge to the fixed point. Using the implicit function theorem we are going to
verify that the function h is differentiable.
(3) Differentiability of h. We define the functions F and G by
F W X E
C
! X; F.x; a/ ´ F
a
.x/
and
G W X E
C
! X; G.x; a/ ´ x F.x;a/;
and observe that if g 2 C
k
for an integer k 1, then also the maps F and G are
of class C
k
.The solution set, consisting of the points .x; a/ 2 X E
C
which solve
the equation G.x; a/ D 0, is known to us, namely,
G.x; a/ D 0 () .x; a/ D .x.a/; a/;
where x.a/ 2 X is the fixed point of the map F
a
. Therefore,
G.x.a/; a/ D 0; a 2 E
C
:
We now use the implicit function theorem as a regularity theorem. We denote
by D
1
D
@
@x
the derivative in the first variable. If D
1
G.x; a/ 2 L.X; X / is a
continuous isomorphism of the Banach space X , then the implicit function theorem
guarantees that the function a 7! x.a/W E
C
! X belongs to C
k
.Wehave
D
1
G.x; a/ D 1 D
1
F.x;a/ 2 L.X/
and we show that the operator norm satisfies kD
1
F.x;a/k<1. From the
theorem of Neumann it then follows that the bounded linear map D
1
G.x; a/ is a
continuous isomorphism of the Banach space.
In order to estimate this operator norm we take an element y D .y
j
/
j 0
2 X
and express D
1
F.x;a/y 2 X in components. This means for j 1 that
ŒD
1
F.x;a/y
j
D AP
C
y
j 1
C P
C
g
0
.x
j 1
/y
j 1
C A
1
P
y
j C1
A
1
g
0
.x
j
/y
j
and for j D 0,
ŒD
1
F.x;a/y
0
D A
1
P
y
1
A
1
P
g
0
.x
0
/y
0
:
As in the proof of Lemma II.9 one proves (now D 1) the estimates
ˇ
ˇ
ŒD
1
F.x;a/y
j
ˇ
ˇ
.˛ Cı/kykkyk
for j 0. Taking the supremum over j 0, we obtain kD
1
F.x;a/ykkyk.
This holds true for every y 2 X. Therefore, taking the supremum over all y
satisfying kyk1, we obtain the desired estimate of the operator norm:
kD
1
F.x;a/k<1:
II.2. Local invariant manifolds 67
(4) We finally prove that h
0
.0/ D 0 2 L.E
C
;E
/. Recalling the definition
h.a/ ´ P
Œx.a/
0
, the differentiation of the function h at the point a gives, for
every b 2 E
C
,
h
0
.a/b D P
D
a
Œx.a/
0
b
D P
ŒD
a
x.a/b
0
:
In view of the fixed point property of x.a/ we have the identity
x.a/ D F .x.a/; a/; a 2 E
C
:
Differentiating this identity in the variable a we obtain by the chain rule,
D
a
x.a/b D D
1
F.x.a/;a/D
a
x.a/b C D
2
F.x.a/;a/b; b 2 E
C
;
where D
2
denotes the derivative in the second argument. Writing for simplicity D
instead of D
a
for the derivative in a,wehaveDx.a/ 2 L.E
C
;X/.Ifa D 0 in
E
C
, then x.0/ D 0 2 X, so that x.0/
j
D 0 for all j 0. Using the assumption
g
0
.0/ D 0 2 L.R
n
/, one concludes
ŒDx.0/b
j
D AP
C
ŒDx.0/b
j 1
C A
1
P
ŒDx.0/b
j C1
for j 1, and for j D 0,
ŒDx.0/b
0
D A
1
P
ŒDx.0/b
1
C b:
Applying the projection operator P
to both sides and observing P
P
C
D 0 we
obtain the equations
P
ŒDx.0/b
j
D A
1
P
ŒDx.0/b
j C1
;j 0;
from which we deduce the estimates
jP
ŒDx.0/b
j
j˛jP
ŒDx.0/b
j C1
j;j 0;
so that
kP
Dx.0/bk˛kP
Dx.0/bk:
Since ˛<1, this means that P
Dx.0/b D 0 and so
h
0
.0/b D P
ŒDx.0/b
0
D 0
for all b 2 E
C
, hence h
0
.0/ D 0, as claimed.
We have proved the statement of the theorem for the local stable invariant mani-
fold. The analogous statement for the local unstable invariant manifold W
loc
.R
n
/
is proved the same way. Hence, the proof of Theorem II.8 is complete.

68 Chapter II. Invariant manifolds of hyperbolic fixed points
After these preparations, we shall prove the theorem of Hadamard and Perron.
Proof of Theorem II.7. The proof of the local Theorem II.7 will be a consequence of
Theorem II.8. We modify the diffeomorphism ' of Theorem II.7 outside of an open
neighborhood of the origin. For this, we take the cut-off function 2 C
1
.R; Œ0; 1/
satisfying
.t/ D 1; t 1=2;
.t/ D 0; t 1
and define the modified maps
Q'.x/ ´ Ax CQg.x/ ´ Ax C
jxj
"
g.x/:
Then,
Q'.x/ D
´
'.x/; jxj"=2;
Ax; jxj":
Foragivenı>0we can, due to our assumptions g.0/ D 0 and g
0
.0/ D 0, find an
">0sufficiently small such that
jQg
0
.x/j <ı; x2 R
n
:
Therefore, for a suitable ı>0, the modified diffeomorphism Q' meets the assump-
tions of Theorem II.8. Next, we choose the neighborhood Q of the origin as in
Theorem II.7 so small that
Q'.x/ D '.x/; x 2 Q:
Lemma II.10. For the neighborhood Q ´fx D .x
C
;x
/ 2 E
C
˚ E
jjx
C
j
r; jx
jrg the following holds true:
W
C
loc
.Q/ D W
C
loc
.R
n
; Q'/ \ Q;
if r>0is sufficiently small.
.t/
t
0
1
1
2
Figure II.7. The cut-off function .
II.3. Stable and unstable invariant manifolds 69
Proof. Due to Q' D ' in Q we clearly have the inclusion
W
C
loc
.Q/ W
C
loc
.R
n
; Q'/ \ Q:
In order to prove the opposite inclusion we take x 2 W
C
loc
. Q'/ \Q and show that its
image y D .y
C
;y
/ ´ '.x/ lies in Q. By repeating the argument it then follows
that the positive orbit of x lies in Q and the lemma follows. Recall now that the
map '.x/ D Ax C g.x/ is of the form
y
C
D A
C
x
C
C g
C
.x/;
y
D A
x
C g
.x/:
Since x 2 W
C
loc
. Q'/, we know from Theorem II.8 that x
D h.x
C
/. Because the
maps h; h
0
;g;g
0
all vanish in 0, there exists for every ">0an r>0such that
jg.x/j"r and jh.x
C
/j"r
if jxjr (note that from jxjr, it follows that jx
C
jr). Since ˛<1, we can
choose " so small that
jy
C
jkA
C
kjx
C
jCjg
C
.x/j˛r C "r < r
and
jy
jkA
kjh.x
C
/jCjg
.x/jkA
k"r C "r < r:
Hence, y 2 Q, and the lemma follows.
In view of this lemma we finally obtain from Theorem II.8,
W
C
loc
.Q/ D W
C
loc
.R
n
; Q'/ \ Q
D graph.h/ \ Q
Dfx 2 Q j x D .x
C
; h.x
C
// 2 E
C
˚ E
g:
This is the statement of Theorem II.7 for the stable local invariant manifold. The
proof for the unstable local invariant manifold W
loc
is analogous. This completes
the proof of Theorem II.7.
II.3 Stable and unstable invariant manifolds
Theorem II.7 demonstrates that locally the stable and unstable manifolds of the dif-
feomorphism ' W R
n
! R
n
issuing from the hyperbolic fixed point 0 are embedded
submanifolds in an open neighborhood of the fixed point. Globally, this is not nec-
essarily true anymore. Indeed, in contrast to the statement of Theorem II.8 the stable
and unstable invariant manifolds can globally pile up on themselves, as we shall see
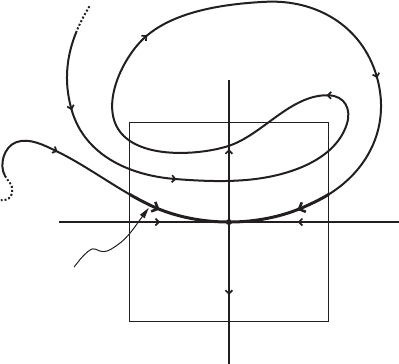
70 Chapter II. Invariant manifolds of hyperbolic fixed points
0
E
C
E
W
C
.'; 0/
W
C
loc
.Q/
Q
Figure II.8. The stable invariant manifold W
C
.'; 0/.
later on. Let us first recall the definitions of the stable invariant manifold W
C
.0; '/
and the unstable invariant manifold W
.0; '/ making use of Theorem II.7,
W
C
.0; '/ ´fx 2 R
n
j '
j
.x/ ! 0; j ! C1g
D
[
n0
'
n
.W
C
loc
.Q//;
W
.0; '/ ´fx 2 R
n
j '
j
.x/ ! 0; j ! C1g
D
[
n0
'
n
.W
loc
.Q//:
It turns out that these two sets can be parametrized globally by their tangent
spaces at the hyperbolic fixed point, hence, in the notation of Theorem II.7, by the
Euclidean spaces E
C
and E
. This is the statement of the following theorem of
S. Smale in which we make use of the notation of Theorem II.7.
Theorem II.11 (S. Smale). Assume 0 to be a hyperbolic fixed point of the C
k
-
diffeomorphism ' W R
n
! R
n
, for k 1. Then, the stable invariant manifold
W
C
.0; '/ R
n
is the image of an injective C
k
-immersion j of the tangent space
E
C
´ T
0
W
C
loc
.Q/ into R
n
, i.e., there exists a map
j W E
C
! R
n
of class C
k
having the following properties:
