Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.

82 | I. Motivation and Foundation
so that ∂
μ
ϕ(x) is a vector field. Given two vector fields A
μ
(x) and B
ν
(x), we can contract
them with g
μν
(x) to form g
μν
(x)A
μ
(x)B
ν
(x), which, as you can immediately check, is
a scalar. In particular, g
μν
(x)∂
μ
ϕ(x)∂
ν
ϕ(x) is a scalar. Thus, if we simply replace the
Minkowski metric η
μν
in the Lagrangian L =
1
2
[(∂ϕ)
2
−m
2
ϕ
2
] =
1
2
(η
μν
∂
μ
ϕ∂
ν
ϕ − m
2
ϕ
2
) by
the Einstein metric g
μν
, the Lagrangian is invariant under coordinate transformation.
The action is obtained by integrating the Lagrangian over spacetime. Under a coordinate
transformation d
4
x
= d
4
x det(∂x
/∂x). Taking the determinant of (1), we have
g ≡ det g
μν
= det g
λσ
∂x
λ
∂x
μ
∂x
σ
∂x
ν
= g
det
∂x
∂x
2
(2)
We see that the combination d
4
x
√
−g =d
4
x
−g
is invariant under coordinate transfor-
mation.
Thus, given a quantum field theory we can immediately write down the theory in curved
spacetime. All we have to do is promote the Minkowski metric η
μν
in our Lagrangian to the
Einstein metric g
μν
and include a factor
√
−g in the spacetime integration measure.
2
The
action S would then be invariant under arbitrary coordinate transformations. For example,
the action for a scalar field in curved spacetime is simply
S =
d
4
x
√
−g
1
2
(g
μν
∂
μ
ϕ∂
ν
ϕ − m
2
ϕ
2
) (3)
(There is a slight subtlety involving the spin
1
2
field that we will talk about in part II. We
will eventually come to it in chapter VIII.1.)
There is no essential difficulty in quantizing the scalar field in curved spacetime. We
simply treat g
μν
as given [e.g., the Schwarzschild metric in spherical coordinates: g
00
=
(1 − 2GM/r), g
rr
=−(1 − 2GM/r)
−1
, g
θθ
=−r
2
, and g
φφ
=−r
2
sin
2
θ] and study the
path integral
Dϕe
iS
, which is still a Gaussian integral and thus do-able. The propagator
of the scalar field D(x, y) can be worked out and so on and so forth. (see exercise I.11.1).
At this point, aside from the fact that g
μν
(x) carries Lorentz indices while ϕ(x) does not,
the metric g
μν
looks just like a field and is in fact a classical field. Write the action of the
world S =S
g
+S
M
as the sum of two terms: S
g
describing the dynamics of the gravitational
field g
μν
(which we will come to in chapter VIII.1) and S
M
describing the dynamics of all
the other fields in the world [the “matter fields,” namely ϕ in our simple example with S
M
as given in (3)]. We could quantize gravity by integrating over g
μν
as well, thus extending
the path integral to
DgDϕe
iS
.
Easier said than done! As you have surely heard, all attempts to integrate over g
μν
(x)
have been beset with difficulties, eventually driving theorists to seek solace in string theory.
I will explain in due time why Einstein’s theory is known as “nonrenormalizable.”
2
We also have to replace ordinary derivatives ∂
μ
by the covariant derivatives D
μ
of general relativity, but acting
on a scalar field ϕ the covariant derivative is just the ordinary derivative D
μ
ϕ = ∂
μ
ϕ.
I.11. Field Theory in Spacetime | 83
What the graviton listens to
One of the most profound results to come out of Einstein’s theory of gravity is a funda-
mental definition of energy and momentum. What exactly are energy and momentum any
way? Energy and momentum are what the graviton listens to. (The graviton is of course
the particle associated with the field g
μν
.)
The stress-energy tensor T
μν
is defined as the variation of the matter action S
M
with
respect to the metric g
μν
(holding the coordinates x
μ
fixed):
T
μν
(x) =−
2
√
−g
δS
M
δg
μν
(x)
(4)
Energy is defined as E =P
0
=
d
3
x
√
−gT
00
(x) and momentum as P
i
=
d
3
x
√
−gT
0i
(x).
Even if we are not interested in curved spacetime per se, (4) still offers us a simple (and
fundamental) way to determine the stress energy of a field theory in flat spacetime. We
simply vary around the Minkowski metric η
μν
by writing g
μν
=η
μν
+h
μν
and expand S
M
to first order in h. According to (4), we have
3
S
M
(h) = S
M
(h = 0) −
d
4
x
1
2
h
μν
T
μν
+ O(h
2
)
. (5)
The symmetric tensor field h
μν
(x) is in fact the graviton field (see chapters I.5 and
VIII.1). The stress-energy tensor T
μν
(x) is what the graviton field couples to, just as the
electromagnetic current J
μ
(x) is what the photon field couples to.
Consider a general S
M
=
d
4
x
√
−g(A + g
μν
B
μν
+ g
μν
g
λρ
C
μνλρ
+
...
). Since −g =
1 + η
μν
h
μν
+ O(h
2
) and g
μν
= η
μν
− h
μν
+ O(h
2
), we find
T
μν
= 2(B
μν
+ 2C
μνλρ
η
λρ
+
...
) − η
μν
L (6)
in flat spacetime. Note
T ≡ η
μν
T
μν
=−(4A + 2η
μν
B
μν
+ 0
.
η
μν
η
λρ
C
μνλρ
+
...
) (7)
which we have written in a form emphasizing that C
μνλρ
does not contribute to the trace
of the stress-energy tensor.
We now show the power of this definition of T
μν
by obtaining long-familiar results
about the electromagnetic field. Promoting the Lagrangian of the massive spin 1 field
to curved spacetime we have
4
L = (−
1
4
g
μν
g
λρ
F
μλ
F
νρ
+
1
2
m
2
g
μν
A
μ
A
ν
) and thus
5
T
μν
=
−F
μλ
F
λ
ν
+ m
2
A
μ
A
ν
− η
μν
L.
3
I use the normal convention in which indices are summed regardless of any symmetry; in other words,
1
2
h
μν
T
μν
=
1
2
(h
01
T
01
+ h
10
T
10
+
...
) = h
01
T
01
+
...
.
4
Here we use the fact that the covariant curl is equal to the ordinary curl D
μ
A
ν
−D
ν
A
μ
=∂
μ
A
ν
−∂
ν
A
μ
and
so F
μν
does not involve the metric.
5
Holding x
μ
fixed means that we hold ∂
μ
and hence A
μ
fixed since A
μ
is related to ∂
μ
by gauge invariance.
We are anticipating (see chapter II.7) here, but you have surely heard of gauge invariance in a nonrelativistic
context.

84 | I. Motivation and Foundation
For the electromagnetic field we set m = 0. First, L =−
1
4
F
μν
F
μν
=−
1
4
(−2F
2
0i
+F
2
ij
) =
1
2
(
E
2
−
B
2
). Thus, T
00
=−F
0λ
F
λ
0
−
1
2
(
E
2
−
B
2
) =
1
2
(
E
2
+
B
2
). That was comforting, to
see a result we knew from “childhood.” Incidentally, this also makes clear that we can
think of
E
2
as kinetic energy and
B
2
as potential energy. Next, T
0i
=−F
0λ
F
λ
i
= F
0j
F
ij
=
ε
ij k
E
j
B
k
= (
E ×
B)
i
. The Poynting vector has just emerged.
Since the Maxwell Lagrangian L =−
1
4
g
μν
g
λρ
F
μλ
F
νρ
involves only the C term with
C
μνλρ
=−
1
4
F
μν
F
λρ
, we see from (7) that the stress-energy tensor of the electromagnetic
field is traceless, an important fact we will need in chapter VIII.1. We can of course check
directly that T =0 (exercise I.11.4).
6
Appendix: A concise introduction to curved spacetime
General relativity is often made to seem more difficult and mysterious than need be. Here I give a concise review
of some of its basic elements for later use.
Denote the spacetime coordinates of a point particle by X
μ
. To construct its action note that the only
coordinate invariant quantity is the “length”
7
of the world line traced out by the particle (fig. I.11.1), namely
ds =
g
μν
dX
μ
dX
ν
, where g
μν
is evaluated at the position of the particle of course. Thus, the action for a
point particle must be proportional to
ds =
g
μν
dX
μ
dX
ν
=
g
μν
[X(ζ)]
dX
μ
dζ
dX
ν
dζ
dζ
where ζ is any parameter that varies monotonically along the world line. The length, being geometric, is
manifestly reparametrization invariant, that is, independent of our choice of ζ as long as it is reasonable. This
is one of those “more obvious than obvious” facts since
g
μν
dX
μ
dX
ν
is manifestly independent of ζ .Ifwe
insist, we can check the reparametrization invariance of
ds. Obviously the powers of dζ match. Explicitly, if
we write ζ = ζ(η), then dX
μ
/dζ = (dη/dζ )(dX
μ
/dη) and dζ = (dζ /dη)dη.
Let us define
K ≡ g
μν
[X(ζ)]
dX
μ
dζ
dX
ν
dζ
for ease of writing. Setting the variation of
dζ
√
K equal to zero, we obtain
dζ
1
√
K
(2g
μν
dX
μ
dζ
dδX
ν
dζ
+ ∂
λ
g
μν
dX
μ
dζ
dX
ν
dζ
δX
λ
) = 0
which upon integration by parts (and with δX
λ
= 0 at the endpoints as usual) gives the equation of motion
√
K
d
dζ
1
√
K
2g
μλ
dX
μ
dζ
− ∂
λ
g
μν
dX
μ
dζ
dX
ν
dζ
= 0 (8)
To simplify (8) we exploit our freedom in choosing ζ and set dζ = ds, so that K =1. We have
2g
μλ
d
2
X
μ
ds
2
+ 2∂
σ
g
μλ
dX
σ
ds
dX
μ
ds
− ∂
λ
g
μν
dX
μ
ds
dX
ν
ds
= 0
6
We see that tracelessness is related to the fact that the electromagnetic field has no mass scale. Pure
electromagnetism is said to be scale or dilatation invariant. For more on dilatation invariance see S. Coleman,
Aspects of Symmetry,p.67.
7
We put “length” in quotes because if g
μν
had a Euclidean signature then
ds would indeed be the length
and minimizing
ds would give the shortest path (the geodesic) between the endpoints, but here g
μν
has a
Minkowskian signature.
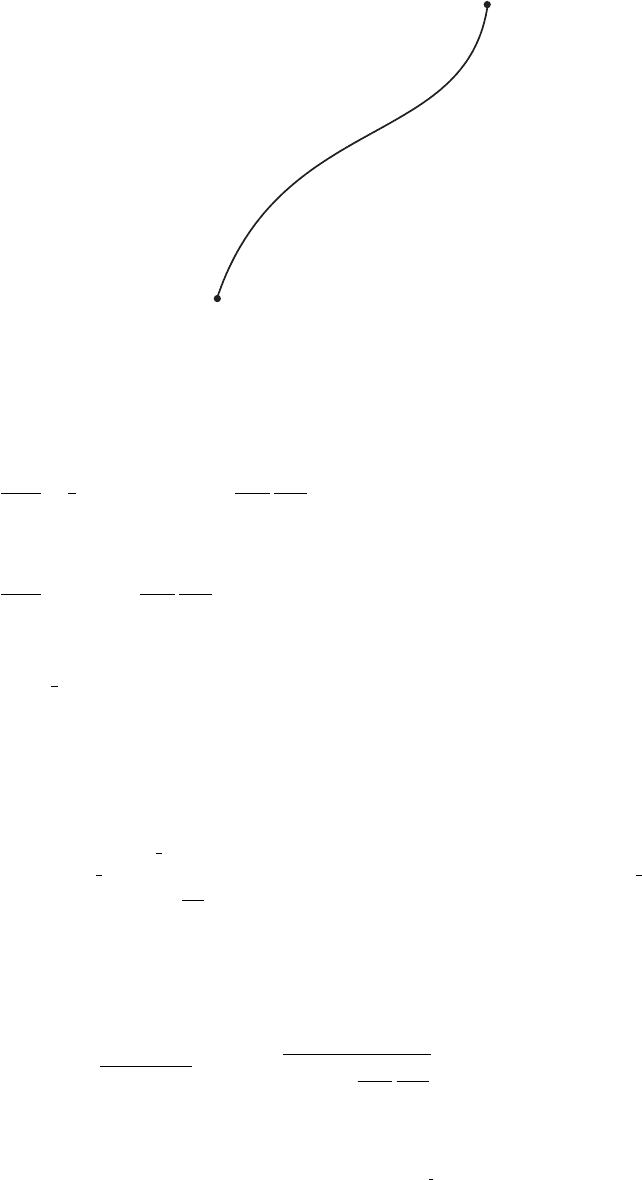
I.11. Field Theory in Spacetime | 85
X
μ
(ζ)
Figure I.11.1
which upon multiplication by g
ρλ
becomes
d
2
X
ρ
ds
2
+
1
2
g
ρλ
(2∂
ν
g
μλ
− ∂
λ
g
μν
)
dX
μ
ds
dX
ν
ds
= 0
that is,
d
2
X
ρ
ds
2
+
ρ
μν
[X(s)]
dX
μ
ds
dX
ν
ds
= 0 (9)
if we define the Riemann-Christoffel symbol by
ρ
μν
≡
1
2
g
ρλ
(∂
μ
g
νλ
+ ∂
ν
g
μλ
− ∂
λ
g
μν
) (10)
Given the initial position X
μ
(s
0
) and velocity (dX
μ
/ds)(s
0
) we have four second order differential equations (9)
determining the geodesic followed by the particle in curved spacetime. Note that, contrary to the impression
given by some texts, unlike (8), (9) is not reparametrization invariant.
To recover Newtonian gravity, three conditions must be met: (1) the particle moves slowly dX
i
/ds dX
0
/ds;
(2) the gravitational field is weak, so that the metric is almost Minkowskian g
μν
η
μν
+ h
μν
; and (3) the
gravitational field does not depend on time. Condition (1) means that d
2
X
ρ
/ds
2
+
ρ
00
(dX
0
/ds)
2
0, while (2)
and (3) imply that
ρ
00
−
1
2
η
ρλ
∂
λ
h
00
. Thus, (9) reduces to d
2
X
0
/ds
2
0 (which implies that dX
0
/ds is a constant)
and d
2
X
i
/ds
2
+
1
2
∂
i
h
00
(dX
0
/ds)
2
0, which since X
0
is proportional to s becomes d
2
X
i
/dt
2
−
1
2
∂
i
h
00
. Thus,
we obtain Newton’s equation
d
2
X
dt
2
−
∇φ if we define the gravitational potential φ by h
00
= 2φ:
g
00
1 + 2φ (11)
Referring to the Schwarzschild metric, we see that far from a massive body, φ =−GM/r, as we expect. (Note
also that this derivation depends neither on h
ij
nor on h
0j
, as long as they are time independent.)
Thus, the action of a point particle is
S =−m
g
μν
dX
μ
dX
ν
=−m
g
μν
[X(ζ)]
dX
μ
dζ
dX
ν
dζ
dζ (12)
The m follows from dimensional analysis.
A slick way of deriving S (which also allows us to see the minus sign) is to start with the nonrelativistic action
of a particle in a gravitational potential φ, namely S =
Ldt =
(
1
2
mv
2
− m − mφ)dt . Note that the rest mass
86 | I. Motivation and Foundation
m comes in with a minus sign as it is part of the potential energy in nonrelativistic physics. Now force S into a
relativistic form: For small v and φ,
S =−m
(1 −
1
2
v
2
+ φ)dt −m
1 − v
2
+ 2φdt
=−m
(1 + 2φ)(dt)
2
− (d x)
2
We see
8
that the 2 in (11) comes from the square root in the Lorentz-Fitzgerald quantity
√
1 − v
2
.
Now that we have S we can calculate the stress energy of a point particle using (4):
T
μν
(x) =
m
√
−g
dζK
−
1
2
δ
(4)
[x − X(ζ)]
dX
μ
dζ
dX
ν
dζ
Setting ζ to s (which we call the proper time τ in this context) we have
T
μν
(x) =
m
√
−g
dτδ
(4)
[x − X(τ)]
dX
μ
dτ
dX
ν
dτ
In particular, as we expect the 4-momentum of the particle is given by
P
ν
=
d
3
x
√
−gT
0ν
= m
dτδ[x
0
− X
0
(τ )]
dX
0
dτ
dX
ν
dτ
= m
dX
ν
dτ
The action (12) given here has two defects: (1) it is difficult to deal with a path integral
DXe
−im
dζ
√
(dX
μ
/dζ )(dX
μ
/dζ )
involving a square root, and (2) S does not make sense for a massless particle.
To remedy these defects, note that classically, S is equivalent to
S
imp
=−
1
2
dζ
1
γ
dX
μ
dζ
dX
μ
dζ
+ γm
2
(13)
where (dX
μ
/dζ )(dX
μ
/dζ ) = g
μν
(X)(dX
μ
/dζ )(dX
ν
/dζ ). Varying with respect to γ(ζ) we obtain m
2
γ
2
=
(dX
μ
/dζ )(dX
μ
/dζ ). Eliminating γ in S
imp
we recover S.
The path integral
DXe
iS
imp
has a standard quadratic form.
9
Quantum mechanics of a relativistic point parti-
cle is best formulated in terms of S
imp
, not S. Furthermore, for m =0, S
imp
=−
1
2
dζ[γ
−1
(dX
μ
/dζ )(dX
μ
/dζ )]
makes perfect sense. Note that varying with respect to γ now gives the well-known fact that for a massless particle
g
μν
(X)dX
μ
dX
ν
= 0.
The action S
imp
will provide the starting point for our discussion on string theory in chapter VIII.5.
Exercises
I.11.1 Integrate by parts to obtain for the scalar field action
S =−
d
4
x
√
−g
1
2
ϕ(
1
√
−g
∂
μ
√
−gg
μν
∂
ν
+ m
2
)ϕ
8
We should not conclude from this that g
ij
= δ
ij .
The point is that to leading order in v/c, our particle is
sensitive only to g
00
, as we have just shown. Indeed, restoring c in the Schwarzschild metric we have
ds
2
= (1 −
2GM
c
2
r
)c
2
dt
2
− (1 −
2GM
c
2
r
)
−1
dr
2
− r
2
dθ
2
− r
2
sin
2
θdφ
2
→ c
2
dt
2
− d x
2
−
2GM
r
dt
2
+ O(1/c
2
)
9
One technical problem, which we will address in chapter III.4, is that in the integral over X(ζ) apparently
different functions X(ζ) may in fact be the same physically, related by a reparametrization.

I.11. Field Theory in Spacetime | 87
and write the equation of motion for ϕ in curved spacetime. Discuss the propagator of the scalar field
D(x, y) (which is of course no longer translation invariant, i.e., it is no longer a function of x − y).
I.11.2 Use (4) to find E for a scalar field theory in flat spacetime. Show that the result agrees with what you
would obtain using the canonical formalism of chapter I.8.
I.11.3 Show that in flat spacetime P
μ
as derived here from the stress energy tensor T
μν
when interpreted as
an operator in the canonical formalism satisfies [P
μ
, ϕ(x)] =−i∂
μ
ϕ(x), and thus does exactly what you
expect the energy and momentum operators to do, namely to be conjugate to time and space and hence
represented by −i∂
μ
.
I.11.4 Show that for the Maxwell field T
ij
=−(E
i
E
j
+ B
i
B
j
) +
1
2
δ
ij
(
E
2
+
B
2
) and hence T =0.
I.12 Field Theory Redux
What have you learned so far?
Now that we have reached the end of part I, let us take stock of what you have learned.
Quantum field theory is not that difficult; it just consists of doing one great big integral
Z(J) =
Dϕ e
i
d
D+1
x[
1
2
(∂ϕ)
2
−
1
2
m
2
ϕ
2
−λϕ
4
+Jϕ]
(1)
By repeatedly functionally differentiating Z(J) and then setting J = 0 we obtain
Dϕ ϕ(x
1
)ϕ(x
2
)
...
ϕ(x
n
)e
i
d
D+1
x[
1
2
(∂ϕ)
2
−
1
2
m
2
ϕ
2
−λϕ
4
]
(2)
which tells us about the amplitude for n particles associated with the field ϕ to come into
and go out of existence at the spacetime points x
1
, x
2
,
...
, x
n
, interacting with each other
in between. Birth and death, with some kind of life in between.
Ah, if we could only do the integral in (1)! But we can’t. So one way of going about it is
to evaluate the integral as a series in λ :
∞
k=0
(−iλ)
k
k!
Dϕ ϕ(x
1
)ϕ(x
2
)
...
ϕ(x
n
)[
d
D+1
yϕ(y)
4
]
k
e
i
d
D+1
x[
1
2
(∂ϕ)
2
−
1
2
m
2
ϕ
2
]
(3)
To keep track of the terms in the series we draw little diagrams.
Quantum field theorists try to dream up ways to evaluate (1), and failing that, they invent
tricks and methods for extracting the physics they are interested in, by hook and by crook,
without actually evaluating (1).
To see that quantum field theory is a straightforward generalization of quantum me-
chanics, look at how (1) reduces appropriately. We have written the theory in (D + 1)-
dimensional spacetime, that is, D spatial dimensions and 1 temporal dimension. Consider
(1) in (0 + 1)-dimensional spacetime, that is, no space; it becomes
Z(J) =
Dϕ e
i
dt[
1
2
(
dϕ
dt
)
2
−
1
2
m
2
ϕ
2
−λϕ
4
+Jϕ]
(4)
I.12. Field Theory Redux | 89
where we now denote the spacetime coordinate x just by time t . We recognize this as the
quantum mechanics of an anharmonic oscillator with the position of the mass point tied
to the spring denoted by ϕ and with an external force J pushing on the oscillator.
In the quantum field theory (1), each term in the action makes physical sense: The first
two terms generalize the harmonic oscillator to include spatial variations, the third term
the anharmonicity, and the last term an external probe. You can think of a quantum field
theory as an infinite collection of anharmonic oscillators, one at each point in space.
We have here a scalar field ϕ. In previous and future chapters, the notion of field was
and will be generalized ever so slightly: The field can transform according to a nontrivial
representation of the Lorentz group. We have already encountered fields transforming as
a vector and a tensor and will presently encounter a field transforming as a spinor. Lorentz
invariance and whatever other symmetries we have constrain the form of the action. The
integral will look more complicated but the approach is exactly as outlined here.
That’s just about all there is to quantum field theory.
This page intentionally left blank

Part II Dirac and the Spinor
