Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.

62 | I. Motivation and Foundation
and
dq
dt
= i[H , q] = p (3)
In other words, operators constructed out of p and q evolve according to O(t) =
e
iHt
O(0)e
−iHt
. In (1) p and q are understood to be taken at the same time. We obtain
the operator equation of motion ¨q =−V
(q) by combining (2) and (3).
Following Dirac, we invite ourselves to consider at some instant in time the operator
a ≡ (1/
√
2ω)(ωq + ip) with some parameter ω. From (1) we have
[a, a
†
] =1 (4)
The operator a(t) evolves according to
da
dt
= i[H ,
1
√
2ω
(ωq +ip)] =−i
ω
2
ip +
1
ω
V
(q)
which can be written in terms of a and a
†
. The ground state |0is defined as the state such
that a |0=0.
In the special case V
(q) = ω
2
q we get the particularly simple result
da
dt
=−iωa. This is
of course the harmonic oscillator L =
1
2
˙q
2
−
1
2
ω
2
q
2
and H =
1
2
(p
2
+ω
2
q
2
) = ω(a
†
a +
1
2
).
The generalization to many particles is immediate. Starting with
L =
a
1
2
˙q
a
2
− V(q
1
, q
2
,
...
, q
N
)
we have p
a
= δL/δ ˙q
a
and
[p
a
(t), q
b
(t)] =−iδ
ab
(5)
The generalization to field theory is almost as immediate. In fact, we just use our handy-
dandy substitution table (I.3.6) and see that in D−dimensional space L generalizes to
L =
d
D
x{
1
2
( ˙ϕ
2
−(
∇ϕ)
2
− m
2
ϕ
2
) − u(ϕ)} (6)
where we denote the anharmonic term (the interaction term in quantum field theory) by
u(ϕ). The canonical momentum density conjugate to the field ϕ(x, t) is then
π(x, t) =
δL
δ ˙ϕ(x, t)
= ∂
0
ϕ(x, t) (7)
so that the canonical commutation relation at equal times now reads [using (I.3.6)]
[π(x, t), ϕ(x
, t)] =[∂
0
ϕ(x, t), ϕ(x
, t)] =−iδ
(D)
(x −x
) (8)
(and of course also [π(x, t), π(x
, t)] = 0 and [ϕ(x, t), ϕ(x
, t)] = 0.) Note that δ
ab
in (5)
gets promoted to δ
(D)
(x −x
) in (8). You should check that (8) has the correct dimension.
Turning the canonical crank we find the Hamiltonian
H =
d
D
x[π(x, t)∂
0
ϕ(x, t) −L]
=
d
D
x{
1
2
[π
2
+ (
∇ϕ)
2
+ m
2
ϕ
2
] +u(ϕ)} (9)
I.8. Quantizing Canonically | 63
For the case u = 0, corresponding to the harmonic oscillator, we have a free scalar field
theory and can go considerably farther. The field equation reads
(∂
2
+ m
2
)ϕ = 0 (10)
Fourier expanding, we have
ϕ(x, t) =
d
D
k
(2π)
D
2ω
k
[a(
k)e
−i(ω
k
t−
k
.
x)
+ a
†
(
k)e
i(ω
k
t−
k
.
x)
] (11)
with ω
k
=+
k
2
+ m
2
so that the field equation (10) is satisfied. The peculiar looking factor
(2ω
k
)
−
1
2
is chosen so that the canonical relation
[a(
k), a
†
(
k
)] =δ
(D)
(
k −
k
) (12)
appropriate for creation and annihilation operators implies the canonical commutation
[∂
0
ϕ(x, t), ϕ(x
, t)] =−iδ
(D)
(x −x
) in (8 ). You should check this but you can see why the
factor (2ω
k
)
−
1
2
is needed since in ∂
0
ϕ a factor ω
k
is brought down from the exponential.
As in quantum mechanics, the vacuum or ground state ||0 is defined by the condition
a(
k)|0=0 for all
k and the single particle state by |
k≡a
†
(
k)|0. Thus, for example,
using (12) we have 0|ϕ(x , t)|
k=(1/
(2π)
D
2ω
k
)e
−i(ω
k
t−
k
.
x)
, which we could think of
as the relativistic wave function of a single particle with momentum
k. For later use, we
will write this more compactly as (1/ρ(k))e
−ik
.
x
, with ρ(k) ≡
(2π)
D
2ω
k
a normalization
factor and k
0
= ω
k
.
To make contact with the path integral formalism let us calculate 0|ϕ(x, t)ϕ(
0, 0) |0
for t>0. Of the four terms a
†
a
†
, a
†
a, aa
†
, and aa in the product of the two fields
only aa
†
survives, and thus using (12) we obtain
[d
D
k/(2π)
D
2ω
k
]e
−i(ω
k
t−
k
.
x)
. In other
words, if we define the time-ordered product T [ϕ(x)ϕ(y)] =θ(x
0
−y
0
)ϕ(x)ϕ(y) +θ(y
0
−
x
0
)ϕ(y)ϕ(x),wefind
0|T [ϕ(x, t)ϕ(
0, 0)]|0=
d
D
k
(2π)
D
2ω
k
[θ(t)e
−i(ω
k
t−
k
.
x)
+ θ(−t)e
+i(ω
k
t−
k
.
x)
] (13)
Go back to (I.3.23). We discover that 0|T [ϕ(x)ϕ(0)]|0=iD(x), the propagator for a
particle to go from 0 to x we obtained using the path integral formalism. This further
justifies the iε prescription in (I.3.22). The physical meaning is that we always create
before we annihilate, not the other way around. This is a form of causality as formulated
in quantum field theory.
A remark: The combination d
D
k/(2ω
k
), even though it does not look Lorentz invariant,
is in fact a Lorentz invariant measure. To see this, we use (I.2.13) to show that (exercise I.8.1)
d
(D+1)
kδ(k
2
− m
2
)θ(k
0
)f (k
0
,
k) =
d
D
k
2ω
k
f(ω
k
,
k) (14)
for any function f(k). Since Lorentz transformations cannot change the sign of k
0
, the step
function θ(k
0
) is Lorentz invariant. Thus the left-hand side is manifestly Lorentz invariant,
and hence the right-hand side must also be Lorentz invariant. This shows that relations
such as (13) are Lorentz invariant; they are frame-independent statements.
64 | I. Motivation and Foundation
Scattering amplitude
Now that we have set up the canonical formalism it is instructive to see how the invariant
amplitude M defined in the preceding chapter arises using this alternative formalism. Let
us calculate the amplitude
k
3
k
4
|e
−iHT
|
k
1
k
2
=
k
3
k
4
|e
i
d
4
xL(x)
|
k
1
k
2
for meson scatter-
ing
k
1
+
k
2
→
k
3
+
k
4
in order λ with u(ϕ) =
λ
4!
ϕ
4
. (We have, somewhat sloppily, turned
the large transition time T into
dx
0
when going over to the Lagrangian.) Expanding in
λ, we obtain (−i
λ
4!
)
d
4
x
k
3
k
4
|ϕ
4
(x) |
k
1
k
2
.
The calculation of the matrix element is not dissimilar to the one we just did for the
propagator. There we have the product of two field operators between the vacuum state.
Here we have the product of four field operators, all evaluated at the same spacetime point
x, sandwiched between two-particle states. There we look for a term of the form a(
k)a
†
(
k),
Here, plugging the expansion (11) of the field into the product ϕ
4
(x), we look for terms of
the form a
†
(
k
4
)a
†
(
k
3
)a(
k
2
)a(
k
1
), so that we could remove the two incoming particles and
produce the two outgoing particles. (To avoid unnecessary complications we assume that
all four momenta are different.) We now annihilate and create. The annihilation operator
a(
k
1
) could have come from any one of the four ϕ fields in ϕ
4
, giving a factor of 4, a(
k
1
)
could have come from any one of the three remaining ϕ fields, giving a factor of 3, a
†
(
k
3
)
could have come from either of the two remaining ϕ fields, giving a factor of 2, so that we
end up with a factor of 4!, which cancels the factor of
1
4!
included in the definition of λ.
(This is of course why, for the sake of convenience, λ is defined the way it is. Recall from
the preceding chapter an analogous step.)
As you just learned and as you can see from (11), we obtain a factor of 1/ρ(k)e
−ik
.
x
for
each incoming particle and of 1/ρ(k)e
+ik
.
x
for each outgoing particle, giving all together
4
α=1
1
ρ(k
α
)
d
4
xe
i(k
3
+k
4
−k
1
−k
2
)
.
x
=
4
α=1
1
ρ(k
α
)
(2π)
4
δ
4
(k
3
+ k
4
− k
1
− k
2
)
It is conventional to refer to S
fi
=f |e
−iHT
|i, with some initial and final state, as
elements of an “S-matrix” and to define the “transition matrix” T -matrix by S = I + iT ,
that is,
S
fi
= δ
fi
+ iT
fi
(15)
In general, for initial and final states consisting of scalar particles characterized only by
their momenta, we write (using an obvious notation, for example
i
k is the sum of the
particle momenta in the initial state), invoking momentum conservation:
iT
fi
= (2π)
4
δ
4
⎛
⎝
f
k −
i
k
⎞
⎠
α
1
ρ(k
α
)
M(f ← i) (16)
In our simple example, iT (
k
3
k
4
,
k
1
k
2
) = (−i
λ
4!
)
d
4
x
k
3
k
4
|ϕ
4
(x) |
k
1
k
2
, and our little cal-
culation showed that M =−iλ, precisely as given in the preceding chapter. But this con-
nection between T
fi
and M, being “merely” kinematical, should hold in general, with the
invariant amplitude M determined by the Feynman rules. I will not give a long boring for-

I.8. Quantizing Canonically | 65
mal proof, but you should check this assertion by working out some more involved cases,
such as the scattering amplitude to order λ
2
, recovering (I.7.23), for example.
Thus, quite pleasingly, we see that the invariant amplitude M determined by the
Feynman rules represents the “heart of the matter” with the momentum conservation
delta function and normalization factors stripped away.
My pedagogical aim here is merely to make one more contact (we will come across
more in later chapters) between the canonical and path integral formalisms, giving
the simplest possible example avoiding all subtleties and complications. Those readers
into rigor are invited to replace the plane wave states |
k
1
k
2
with wave packet states
d
3
k
1
d
3
k
2
f
1
(
k
1
)f
2
(
k
2
) |
k
1
k
2
for some appropriate functions f
1
and f
2
, starting in the
far past when the wave packets were far apart, evolving into the far future, so on and so
forth, all the while smiling with self-satisfaction. The entire procedure is after all no differ-
ent from the treatment of scattering
1
in elementary nonrelativistic quantum mechanics.
Complex scalar field
Thus far, we have discussed a hermitean (often called real in a minor abuse of terminology)
scalar field. Consider instead (as we will in chapter I.10) a nonhermitean (usually called
complex in another minor abuse) scalar field governed by L = ∂ϕ
†
∂ϕ − m
2
ϕ
†
ϕ.
Again, following Heisenberg, we find the canonical momentum density conjugate to
the field ϕ(x, t), namely π(x , t) = δL/[δ ˙ϕ(x, t)] = ∂
0
ϕ
†
(x , t), so that [π(x, t), ϕ(x
, t)] =
[∂
0
ϕ
†
(x , t), ϕ(x
, t)] =−iδ
(D)
(x −x
). Similarly, the canonical momentum density conju-
gate to the field ϕ
†
(x , t) is ∂
0
ϕ(x, t).
Varying ϕ
†
we obtain the Euler-Lagrange equation of motion (∂
2
+m
2
)ϕ = 0. [Similarly,
varying ϕ we obtain (∂
2
+ m
2
)ϕ
†
= 0.] Once again, we could Fourier expand, but now the
nonhermiticity of ϕ means that we have to replace (11) by
ϕ(x, t) =
d
D
k
(2π)
D
2ω
k
a(
k)e
−i(ω
k
t−
k
.
x)
+ b
†
(
k)e
i(ω
k
t−
k
.
x))
(17)
In (11) hermiticity fixed the second term in the square bracket in terms of the first. Here
in contrast, we are forced to introduce two independent sets of creation and annihilation
operators (a, a
†
) and (b, b
†
). You should verify that the canonical commutation relations
imply that these indeed behave like creation and annihilation operators.
Consider the current
J
μ
= i(ϕ
†
∂
μ
ϕ − ∂
μ
ϕ
†
ϕ) (18)
Using the equations of motion you should check that ∂
μ
J
μ
= i(ϕ
†
∂
2
ϕ − ∂
2
ϕ
†
ϕ). (This
follows immediately from the fact that the equation of motion for ϕ
†
is the hermitean
1
For example, M. L. Goldberger and K. M. Watson, Collision Theory.

66 | I. Motivation and Foundation
conjugate of the equation of motion for ϕ.) The current is conserved and the corresponding
time-independent charge is given by (verify this!)
Q =
d
D
xJ
0
(x) =
d
D
k[a
†
(
k)a(
k) −b
†
(
k)b(
k)].
Thus the particle created by a
†
(call it the “particle”) and the particle created by b
†
(call it
the “antiparticle”) carry opposite charges. Explicitly, using the commutation relation we
have Qa
†
|0=+a
†
|0 and Qb
†
|0=−b
†
|0.
We conclude that ϕ
†
creates a particle and annihilates an antiparticle, that is, it produces
one unit of charge. The field ϕ does the opposite. You should understand this point
thoroughly, as we will need it when we come to the Dirac field for the electron and positron.
The energy of the vacuum
As an instructive exercise let us calculate in the free scalar field theory the expectation
value 0|H |0=
d
D
x
1
2
0|(π
2
+(
∇ϕ)
2
+m
2
ϕ
2
) |0, which we may loosely refer to as the
“energy of the vacuum.” It is merely a matter of putting together (7), (11), and (12). Let us
focus on the third term in 0|H |0, which in fact we already computed, since
0|ϕ(x, t)ϕ(x , t)|0=0|ϕ(
0, 0)ϕ(
0, 0) |0
= lim
x , t→
0, 0
0|ϕ(x, t)ϕ(
0, 0) |0= lim
x , t→
0, 0
d
D
k
(2π)
D
2ω
k
e
−i(ω
k
t−
k
.
x)
=
d
D
k
(2π)
D
2ω
k
The first equality follows from translation invariance, which also implies that the factor
d
D
x in 0|H |0 can be immediately replaced by V , the volume of space. The calculation
of the other two terms proceeds in much the same way: for example, the two factors of
∇
in (
∇ϕ)
2
just bring down a factor of
k
2
. Thus
0|H |0=V
d
D
k
(2π)
D
2ω
k
1
2
(ω
2
k
+
k
2
+ m
2
) = V
d
D
k
(2π)
D
1
2
ω
k
(19)
upon restoring .
You should find this result at once gratifying and alarming, gratifying because we recog-
nize it as the zero point energy of the harmonic oscillator integrated over all momentum
modes and over all space, and alarming because the integral over
k clearly diverges. But we
should not be alarmed: the energy of any physical configuration, for example the mass of a
particle, is to be measured relative to the “energy of the vacuum.” We ask for the difference
in the energy of the world with and without the particle. In other words, we could simply
define the correct Hamiltonian to be H −0|H |0 . We will come back to some of these
issues in chapters II.5, III.1, and VIII.2.
Nobody is perfect
In the canonical formalism, time is treated differently from space, and so one might worry
about the Lorentz invariance of the resulting field theory. In the standard treatment given
I.8. Quantizing Canonically | 67
in many texts, we would go on from this point and use the Hamiltonian to generate the
dynamics, developing a perturbation theory in the interaction u(ϕ). After a number of
formal steps, we would manage to derive the Feynman rules, which manifestly define a
Lorentz-invariant theory.
Historically, there was a time when people felt that quantum field theory should be
defined by its collection of Feynman rules, which gives us a concrete procedure to calculate
measurable quantities, such as scattering cross sections. An extreme view along this line
held that fields are merely mathematically crutches used to help us arrive at the Feynman
rules and should be thrown away at the end of the day.
This view became untenable starting in the 1970s, when it was realized that there
is a lot more to quantum field theory than Feynman diagrams. Field theory contains
nonperturbative effects invisible by definition to Feynman diagrams. Many of these effects,
which we will get to in due time, are more easily seen using the path integral formalism.
As I said, the canonical and the path integral formalism often appear to be complemen-
tary, and I will refrain from entering into a discussion about which formalism is superior.
In this book, I adopt a pragmatic attitude and use whatever formalism happens to be easier
for the problem at hand.
Let me mention, however, some particularly troublesome features in each of the two
formalisms. In the canonical formalism fields are quantum operators containing an in-
finite number of degrees of freedom, and sages once debated such delicate questions as
how products of fields are to be defined. On the other hand, in the path integral formal-
ism, plenty of sins can be swept under the rug known as the integration measure (see
chapter IV.7).
Appendix 1
It may seem a bit puzzling that in the canonical formalism the propagator has to be defined with time ordering,
which we did not need in the path integral formalism. To resolve this apparent puzzle, it suffices to look at
quantum mechanics.
Let A[q(t
1
)] be a function of q , evaluated at time t
1
. What does the path integral
Dq(t) A[q(t
1
)]e
i
T
0
dtL(˙q , q)
represent in the operator language? Well, working backward to (I.2.4) we see that we would slip A[q(t
1
)] into the
factor q
j+1
|e
−iHδt
|q
j
, where the integer j is determined by the condition that the time t
1
occurs between the
times jδt and (j + 1)δt . In the resulting factor q
j+1
|e
−iHδt
A[q(t
1
)]|q
j
, we could replace the c-number A[q(t
1
)]
by the operator A[ ˆq], since A[ ˆq]|q
j
=A[q
j
]|q
j
A[q(t
1
)]|q
j
to the accuracy we are working with. Note that ˆq is
evidently a Schr
¨
odinger operator. Thus, putting in this factor q
j+1
|e
−iHδt
A[ ˆq]|q
j
together with all the factors of
q
i+1
|e
−iHδt
|q
i
, we find that the integral in question, namely
Dq(t) A[q(t
1
)]e
i
T
0
dtL(˙q , q)
, actually represents
q
F
|e
−iH(T−t
1
)
A[ ˆq]e
−iHt
1
|q
I
=q
F
|e
−iHT
A[ ˆq(t
1
)]|q
I
where ˆq(t
1
) is now evidently a Heisenberg operator. [We have used the standard relation between Heisenberg
and Schr
¨
odinger operators, namely, O
H
(t) = e
iHt
O
S
e
−iHt
.] I find this passage back and forth between the Dirac,
Schr
¨
odinger, and Heisenberg pictures quite instructive, perhaps even amusing.
We are now prepared to ask the more complicated question: what does the path integral
Dq(t) A[q(t
1
)]B[q(t
2
)]e
i
T
0
dtL(˙q , q)
represent in the operator language? Here B[q(t
2
)] is some other function of
q evaluated at time t
2
. So we also slip B[q(t
2
)] into the appropriate factor in (I.2.4) and replace B[q(t
2
)]byB[ ˆq].
But now we see that we have to keep track of whether t
1
or t
2
is the earlier of the two times. If t
2
is earlier, the
operator A[ ˆq] would appear to the left of the operator B[ ˆq], and if t
1
is earlier, to the right. Explicitly, if t
2
is earlier

68 | I. Motivation and Foundation
than t
1
,we would end up with the sequence
e
−iH(T−t
1
)
A[ ˆq]e
−iH(t
1
−t
2
)
B[ ˆq]e
−iHt
2
= e
−iHT
A[ ˆq(t
1
)]B[ ˆq(t
2
)] (20)
upon passing from the Schr
¨
odinger to the Heisenberg picture, just as in the simpler situation above. Thus we
define the time-ordered product
T [A[ ˆq(t
1
)]B[ ˆq(t
2
)]] ≡ θ(t
1
− t
2
)A[ ˆq(t
1
)]B[ ˆq(t
2
)] +θ(t
2
− t
1
)B[ ˆq(t
2
)]A[ ˆq(t
1
)] (21)
We just learned that
q
F
|e
−iHT
T [A[ ˆq(t
1
)]B[ ˆq(t
2
)]] |q
I
=
Dq(t) A[q(t
1
)]B[q(t
2
)]e
i
T
0
dtL(˙q , q)
(22)
The concept of time ordering does not appear on the right-hand side, but is essential on the left-hand side.
Generalizing the discussion here, we see that the Green’s functions G
(n)
(x
1
, x
2
,
...
, x
n
) introduced in the
preceding chapter [see (I.7.13–15)] is given in the canonical formalism by the vacuum expectation value of a time-
ordered product of field operators 0|T {ϕ(x
1
)ϕ(x
2
)
...
ϕ(x
n
)}|0. That (13) gives the propagator is a special case
of this relationship.
We could also consider 0|T {O
1
(x
1
)O
2
(x
2
)
...
O
n
(x
n
)}|0, the vacuum expectation value of a time-ordered
product of various operators O
i
(x) [the current J
μ
(x), for example] made out of the quantum field. Such objects
will appear in later chapters [ for example, (VII.3.7)].
Appendix 2: Field redefinition
This is perhaps a good place to reveal to the innocent reader that there does not exist an international commission
in Brussels mandating what field one is required to use. If we use ϕ, some other guy is perfectly entitled to use
η, assuming that the two fields are related by some invertible function with η = f(ϕ). (To be specific, it is often
helpful to think of η = ϕ + αϕ
3
with some parameter α.) This is known as a field redefinition, an often useful
thing to do, as we will see repeatedly.
The S-matrix amplitudes that experimentalists measure are invariant under field redefinition. But this is
tautological trivia: the scattering amplitude
k
3
k
4
|e
−iHT
|
k
1
k
2
, for example, does not even know about ϕ and η.
The issue is with the formalism we use to calculate the S-matrix.
In the path integral formalism, it is also trivial that we could write Z(J) =
Dη e
i[S(η)+
d
4
xJη]
just as well
as Z(J) =
Dϕ e
i[S(ϕ)+
d
4
xJϕ]
. This result, a mere change of integration variable, was known to Newton and
Leibniz. But suppose we write
˜
Z(J) =
Dϕ e
i[S(ϕ)+
d
4
xJη]
. Now of course any dolt could see that
˜
Z(J) = Z(J),
and a fortiori, the Green’s functions (I.7.14,15) obtained by differentiating
˜
Z(J) and Z(J) are not equal.
The nontrivial physical statement is that the S-matrix amplitudes obtained from
˜
Z(J) and Z(J) are in fact
the same. This better be the case, since we are claiming that the path integral formalism provides a way to actual
physics. To see how this apparent “miracle" (Green’s functions completely different, S-matrix amplitudes the
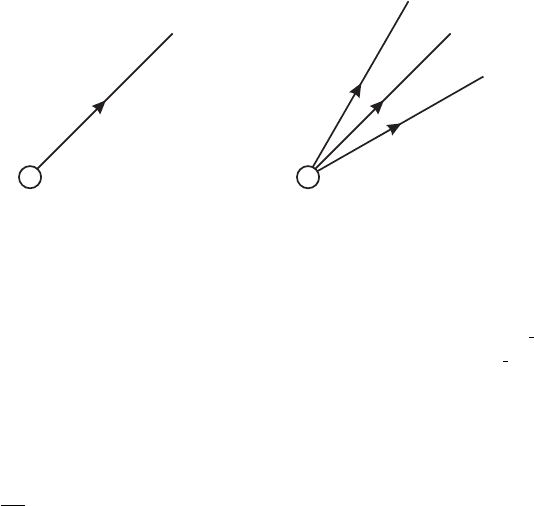
same) occurs, let us think physically. We set up our sources to produce or remove one single field disturbance,
as indicated in figure I.4.1. Our friend, who uses
˜
Z(J), in contrast, set up his sources to produce or remove
η = ϕ + αϕ
3
(we specialize for pedagogical clarity), so that once in a while (with a probability determined by α)
he is producing three field disturbances instead of one, as shown in figure I.8.1. As a result, while he thinks
that he is scattering four mesons, occasionally he is actually scattering six mesons. (Perhaps he should give his
accelerator a tune up.)
But to obtain S-matrix amplitudes we are told to multiply the Green’s functions by (k
2
−m
2
) for each external
leg carrying momentum k, and then set k
2
to m
2
. When we do this, the diagram in figure I.8.1a survives, since
it has a pole that goes like 1/(k
2
− m
2
) but the extraneous diagram in figure I.8.1b is eliminated. Very simple.
One point worth emphasizing is that m here is the actual physical mass of the particle. Let’s be precise when we
should. Take the single particle state |
k. Act on it with the Hamiltonian. Then H |
k=
k
2
+ m
2
|
k. The m that
appears in the eigenvalue of the Hamiltonian is the actual physical mass. We will come back to the issue of the
physical mass in chapter III.3.
In the canonical formalism, the field is an operator, and as we saw just now, the calculation of S-matrix
amplitudes involves evaluating products of field operators between physical states. In particular, the matrix
elements
k|ϕ |0 and 0|ϕ |
k(related by hermitean conjugation) come in crucially. If we use some other field η,
I.8. Quantizing Canonically | 69
(a) (b)
JJ
Figure I.8.1
what matters is merely that
k|η |0 is not zero, in which case we could always write
k|η |0=Z
1
2
k|ϕ |0 with
Z some c-number. We simply divide the scattering amplitude by the appropriate powers of Z
1
2
.
Exercises
I.8.1 Derive (14). Then verify explicitly that d
D
k/(2ω
k
) is indeed Lorentz invariant. Some authors prefer to
replace
2ω
k
in (11) by 2ω
k
when relating the scalar field to the creation and annihilation operators.
Show that the operators defined by these authors are Lorentz covariant. Work out their commutation
relation.
I.8.2 Calculate
k
|H |
k, where |
k=a
†
(
k)|0.
I.8.3 For the complex scalar field discussed in the text calculate 0|T [ϕ(x)ϕ
†
(0)]|0.
I.8.4 Show that [Q, ϕ(x)] =−ϕ(x).

I.9 Disturbing the Vacuum
Casimir effect
In the preceding chapter, we computed the energy of the vacuum 0|H |0 and obtained
the gratifying result that it is given by the zero point energy of the harmonic oscillator
integrated over all momentum modes and over space. I explained that the energy of any
physical configuration, for example, the mass of a particle, is to be measured relative to
this vacuum energy. In effect, we simply subtract off this vacuum energy and define the
correct Hamiltonian to be H −0|H |0.
But what if we disturb the vacuum?
Physically, we could compare the energy of the vacuum before and after we introduce
the disturbance, by varying the disturbance for example. Of course, it is not just our
textbook scalar field that contributes to the energy of the vacuum. The electromagnetic
field, for instance, also undergoes quantum fluctuation and would contribute, with its
two polarization degrees of freedom, to the energy density ε of the vacuum the amount
2
d
3
k/(2π)
3
1
2
ω
k
. In 1948 Casimir had the brilliant insight that we could disturb the
vacuum and produce a shift ε. While ε is not observable, ε should be observable since
we can control how we disturb the vacuum. In particular, Casimir considered introducing
two parallel “perfectly” conducting plates (formally of zero thickness and infinite extent)
into the vacuum. The variation of ε with the distance d between the plates would lead to
a force between the plates, known as the Casimir force. In reality, it is the electromagnetic
field that is responsible, not our silly scalar field.
Call the direction perpendicular to the plates the x axis. Because of the boundary
conditions the electromagnetic field must satisfy on the conducting plates, the wave vector
k can only take on the values (π n/d, k
y
, k
z
), with n an integer. Thus the energy per unit
area between the plates is changed to
n
dk
y
dk
z
/(2π)
2
(πn/d)
2
+ k
2
y
+ k
2
z
.
To calculate the force, we vary d , but then we would have to worry about how the energy
density outside the two plates varies. A clever trick exists for avoiding this worry: we
introduce three plates! See figure (I.9.1). We hold the two outer plates fixed and move
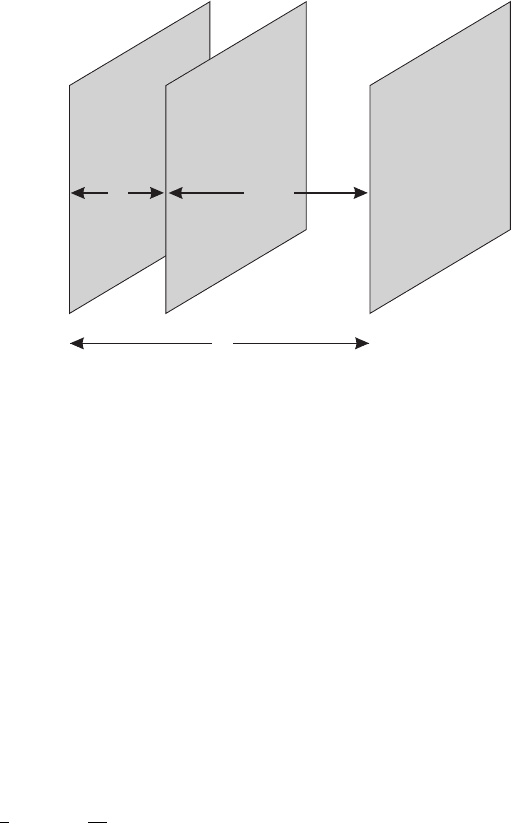
I.9. Disturbing the Vacuum | 71
L
d
L− d
Figure I.9.1
only the inner plate. Now we don’t have to worry about the world outside the plates. The
separation L between the two outer plates can be taken to be as large as we like.
In the spirit of this book (and my philosophy) of avoiding computational tedium as
much as possible, I propose two simplifications: (I) do the calculation for a massless scalar
field instead of the electromagnetic field so we won’t have to worry about polarization
and stuff like that, and (II) retreat to a (1 + 1)-dimensional spacetime so we won’t have
to integrate over k
y
and k
z
. Readers of quantum field theory texts do not need to watch
their authors show off their prowess in doing integrals. As you will see, the calculation is
exceedingly instructive and gives us an early taste of the art of extracting finite physical
results from seemingly infinite expressions, known as regularization, that we will study
in chapters III.1–3.
With this set-up, the energy E = f(d)+ f(L− d) with
f(d)=
1
2
∞
n=1
ω
n
=
π
2d
∞
n=1
n (1)
since the modes are given by sin(nπ x/d) (n = 1,
...
, ∞) with the corresponding energy
ω
n
= nπ/d .
Aagh! What do we do with
∞
n=1
n ? None of the ancient Greeks from Zeno on could tell us.
What they should tell us is that we are doing physics, not mathematics! Physical plates
cannot keep arbitrarily high frequency waves from leaking out.
1
To incorporate this piece of all-important physics, we should introduce a factor e
−aω
n
/π
with a parameter a having the dimension of time (or in our natural units, length) so
that modes with ω
n
π/a do not contribute: they don’t see the plates! The characteristic
1
See footnote 1 in chapter III.1.
