Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

72 | I. Motivation and Foundation

frequency π/a parametrizes the high frequency response of the conducting plates. Thus

we have

f(d)=

∞



n=1

−an/d

=−

∂

∂a

∞



n=1

−an/d

=−

∂

∂a

1 − e

−a/d

a/d

− 1)

Since we want a

−1

to be large, we take the limit a small so that

f(d)=

πd

−

24d

πa

480d

+ O(a

). (2)

Note that f(d)blows up as a → 0, as it should, since we are then back to (1). But the force

between two conducting plates shouldn’t blow up. Experimentalists might have noticed it

by now!

Well, the force is given by

F =−

∂E

∂d

=−{f



(d) − f



(L − d)}=−



2πa

24d

...



−

(

d → L − d

)



−→

a→0

−



−

(L − d)



−→

Ld

−

πc

24d

(3)

Behold, the parameter a we have introduced to make sense of the divergent sum in (1) has

disappeared in our final result for the physically measurable force. In the last step, using

dimensional analysis we restored  to underline the quantum nature of the force.

The Casimir force between two plates is attractive. Notice that the 1/d

of the force

simply follows from dimensional analysis since in natural units force has dimension of

an inverse length squared. In a tour de force, experimentalists have measured this tiny

force. The fluctuating quantum field is quite real!

To obtain a sensible result we need to regularize in the ultraviolet (namely the high

frequency or short time behavior parametrized by a) and in the infrared (namely the long

distance cutoff represented by L). Notice how a and L “work” together in (3).

This calculation foreshadows the renormalization of quantum field theories, a topic

made mysterious and almost incomprehensible in many older texts. In fact, it is perfectly

sensible. We will discuss renormalization in detail in chapters III.1 and III.2, but for now

let us review what we just did.

Instead of panicking when faced with the divergent sum in (1), we remind ourselves

that we are proud physicists and that physics tells us that the sum should not go all the

way to infinity. In a conducting plate, electrons rush about to counteract any applied tan-

gential electric field. But when the incident wave oscillates at sufficiently high frequency,

the electrons can’t keep up. Thus the idealization of a perfectly conducting plate fails. We

regularize (such an ugly term but that’s what field theorists use!) the sum in a mathemati-

cally convenient way by introducing a damping factor. The single parameter a is supposed

to summarize the unknown high frequency physics that causes the electron to fail to keep

up. In reality, a

−1

is related to the plasma frequency of the metal making up the plate.

I.9. Disturbing the Vacuum | 73

A priori, the Casimir force between the two plates could end up depending on the

parameter a. In that case, the Casimir force would tell us something about the response of a

conducting plate to high frequency electric fields, and it would have made for an interesting

chapter in a text on solid state physics. Since this is in fact a quantum field theory text, you

might have suspected that the Casimir force represents some fundamental physics about

fluctuating quantum fields and that a would drop out. That the Casimir force is “universal”

makes it unusually interesting. Notice however, as is physically sensible, that the O(1/d

)

correction to the Casimir force does depend on whether the experimentalist used copper

or aluminum plates.

We might then wonder whether the leading term F =−π/(24d

) depends on the

particular regularization we used. What if we suppress the higher terms in the divergent

sum with some other function? We will address this question in the appendix to this

chapter.

Amusingly, the 24 in (3) is the same 24 that appears in string theory! (The dimension

of spacetime the quantum bosonic string must live in is determined to be 24 + 2 = 26.)

The reader who knows string theory would know what these two cryptic statements are

about (summing up the zero modes of the string). Appallingly, in an apparent attempt to

make the subject appear even more mysterious than it is, some treatments simply assert

that the sum

∞



n=1

n is by some mathematical sleight-of-hand equal to −1/12. Even though

it would have allowed us to wormhole from (1) to (3) instantly, this assertion is manifestly

absurd. What we did here, however, makes physical sense.

Appendix

Here we address the fundamental issue of whether a physical quantity we extract by cutting off high frequency

contributions could depend on how we cut. Let me mention that in recent years the study of Casimir force for

actual physical situations has grown into an active area of research, but clearly my aim here is not to give a realistic

account of this field, but to study in an easily understood context an issue (as you will see) central to quantum

field theory. My hope is that by the time you get to actually regularize a field theory in (3 + 1)-dimensional

spacetime, you would have amply mastered the essential physics and not have to struggle with the mechanics of

regularization.

Let us first generalize a bit the regularization scheme we used and write

f(d)=

∞



n=1





∂

∂a

∞



n=1





≡

∂

∂a





(4)

Here g(v) = h



(v) is a rapidly decreasing function so that the sums make sense, chosen judiciously to allow

ready evaluation of H(a/d)≡

∞



n=1

h(na/d). [In (2), we chose g(v) = e

−v

and hence h(v) =−e

−v

.] We would like

to know how the Casimir force,

−F =

∂f (d)

∂d

− (d → L − d) =

∂

∂d∂a

) − (d → L − d) (5)

depends on g(v).

Let us try to get as far as we can using physical arguments and dimensional analysis. Expand H as follows:

πH (a/d) = ...+γ

−2

+γ

−1

d/a +γ

+γ

a/d + γ

...

. We might be tempted to just write a Taylor

series in a/d, but nothing tells us that H(a/d)might not blow up as a → 0. Indeed, the example in (3) contains

a term like d/a, and so we better be cautious.

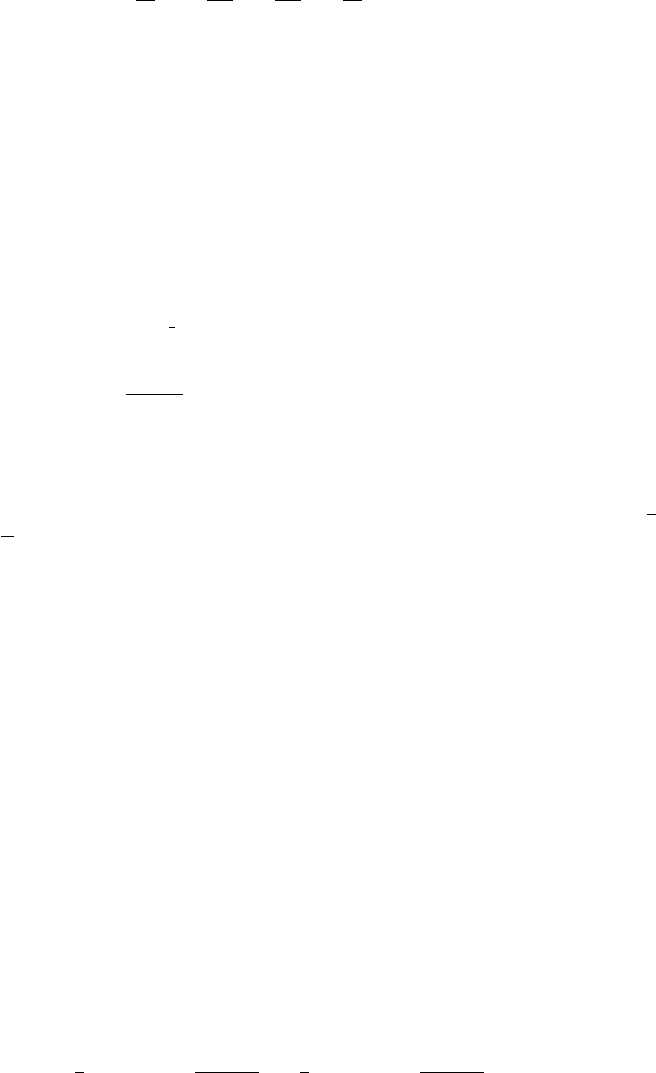
74 | I. Motivation and Foundation

We will presently argue physically that the series in fact terminate in one direction. The force is given by

F =



...+ γ

−2

+ γ

−1

+ γ

...



− (d → L − d) (6)

Look at the γ

−2

term: it contributes to the force a term like (d − (L − d))/a

. But as remarked earlier, the two

outer plates could be taken as far apart as we like. The force could not depend on L, and thus on physical grounds

−2

must vanish. Similarly, all γ

−k

for k>2 must vanish.

Next, we note that the γ

−1

, although definitely not zero, gets subtracted away since it does not depend on d.

(The γ

term has already gone away.) At this point, notice that, furthermore, the γ

terms with k>2 all vanish

as a → 0. You could check that all these assertions hold for the g(v) used in the text.

Remarkably, the Casimir force is determined by γ

alone: F = γ

/(2d

). As noted earlier, the force has to be

proportional to 1/d

. This fact alone shows us that in (6) we only need to keep the γ

term. In the text, we found

=−π/12. In exercise I.9.1 I invite you to go through an amusing calculation obtaining the same value for γ

with an entirely different choice of g(v).

This already suggests that the Casimir force is regularization independent, that it tells us more about the

vacuum than about metallic conductivity, but still it is highly instructive to study an entire class of damping or

regularizing functions to watch how regularization independence emerges. Let us regularize the sum over zero

point energies to f(d)=

∞



n=1

K(ω

) with

K(ω) =





ω + 

(7)

Here c

is a bunch of real numbers and 

(known as regulators or regulator frequencies) a bunch of high

frequencies subject to certain conditions but otherwise chosen entirely at our discretion. For the sum

∞



n=1

K(ω

)

to converge, we need K(ω

) to vanish faster than 1/ω

. In fact, for ω much larger than 

, K(ω) →





−





...

. The requirement that the 1/ω and 1/ω

terms vanish gives the conditions





= 0 (8)

and





= 0 (9)

respectively.

Furthermore, low frequency physics is not to be modified, and so we want K(ω) → 1 for ω<<

, thus

requiring



= 1 (10)

At this point, we do not even have to specify the set the index α runs over beyond the fact that the three conditions

(8),(9), and (10) require that α must take on at least three values. Note also that some of the c

’s must be negative.

Incidentally, we could do with fewer regulators if we are willing to invoke some knowledge of metals, for instance,

that K(ω) = K(−ω), but that is not the issue here.

We now show that the Casimir force between the two plates does not depend on the choices of c

and 

First, being physicists rather than mathematicians, we freely interchange the two sums in f(d)and write

f(d)=







+ 

=−









+ 

(11)

I.9. Disturbing the Vacuum | 75

where, without further ceremony, we have used condition (8). Next, keeping in mind that the sum





/(ω

+ 

) is to be put back into (11), we massage it (defining for convenience b

= π/

) as follows:

∞



n=1



+ 

∞



n=1



∞

dte

−t(1+n

)



∞

dte

−t



1 − e

−

− 1





∞

dte

−t

[

−

12d

+ O





] (12)

(To avoid clutter we have temporarily suppressed the index α.) All these manipulations make perfect sense since

the entire expression is to be inserted into the sum over α in (11) after we restore the index α. It appears that the

result would depend on c

and λ

. In fact, mentally restoring and inserting, we see that the 1/b term in (12) can

be thrown away since





= π





= 0 (13)

[There is in fact a bit of an overkill here since this term corresponds to the γ

−1

term, which does not appear in

the force anyway. Thus the condition (9) is, strictly speaking, not necessary. We are regularizing not merely the

force, but f(d)so that it defines a sensible function.] Similarly, the b

term in (12) can be thrown away thanks

to (8). Thus, keeping only the b term in (12), we obtain

f(d)=−

24d



∞

dte

−t





+ O





=−

24d

+ O





(14)

Indeed, f(d), and a fortiori the Casimir force, do not depend on the c

’s and 

’s. To the level of rigor enter-

tained by physicists (but certainly not mathematicians), this amounts to a proof of regularization independence

since with enough regulators we could approximate any (reasonable) function K(ω) that actually describes real

conducting plates. Again, as is physically sensible, you could check that the O(1/d

) term in f(d)does depend

on the regularization scheme.

The reason that I did this calculation in detail is that we will encounter this class of regularization, known as

Pauli-Villars, in chapter III.1 and especially in the calculation of the anomalous magnetic moment of the electron

in chapter III.7, and it is instructive to see how regularization works in a more physical context before dealing

with all the complications of relativistic field theory.

Exercises

I.9.1 Choose the damping function g(v) = 1/(1 +v)

instead of the one in the text. Show that this re-

sults in the same Casimir force. [Hint: To sum the resulting series, pass to an integral representation

H(ξ)=−

∞



n=1

1/(1 +nξ) =−

∞



n=1



∞

dte

−(1+nξ)t



∞

dte

−t

/(1 − e

ξt

). Note that the integral blows up

logarithmically near the lower limit, as expected.]

I.9.2 Show that with the regularization used in the appendix, the 1/d expansion of the force between two

conducting plates contains only even powers.

I.9.3 Show off your skill in doing integrals by calculating the Casimir force in (3 + 1)-dimensional spacetime.

For help, see M. Kardar and R. Golestanian, Rev. Mod. Phys. 71: 1233, 1999; J. Feinberg, A. Mann, and

M. Revzen, Ann. Phys. 288: 103, 2001.

I.10 Symmetry

Symmetry, transformation, and invariance

The importance of symmetry in modern physics cannot be overstated.

When a law of physics does not change upon some transformation, that law is said to

exhibit a symmetry.

I have already used Lorentz invariance to restrict the form of an action. Lorentz invari-

ance is of course a symmetry of spacetime, but fields can also transform in what is thought

of as an internal space. Indeed, we have already seen a simple example of this. I noted in

passing in chapter I.3 that we could require the action of a scalar field theory to be invariant

under the transformation ϕ →−ϕ and so exclude terms of odd power in ϕ, such as ϕ

from the action.

With the ϕ

term included, two mesons could scatter and go into three mesons, for

example by the diagrams in (fig. I.10.1). But with this term excluded, you can easily

convince yourself that this process is no longer allowed. You will not be able to draw

a Feynman diagram with an odd number of external lines. (Think about modifying the

integral in our baby problem in chapter I.7 to



+∞

−∞

dqe

−

−gq

−λq

+Jq

.) Thus the

simple reflection symmetry ϕ →−ϕ implies that in any scattering process the number

of mesons is conserved modulo 2.

Now that we understand one scalar field, let us consider a theory with two scalar fields

and ϕ

satisfying the reflection symmetry ϕ

→−ϕ

(a = 1or2) :

L =

(∂ϕ

)

−

(∂ϕ

)

−

(1)

We have two scalar particles, call them 1 and 2, with mass m

and m

. To lowest order,

they scatter in the processes 1 + 1 →1 + 1, 2 + 2 → 2 + 2, 1 + 2 → 1 +2, 1 + 1 → 2 + 2,

and 2 + 2 → 1 + 1 (convince yourself). With the five parameters m

, m

, λ

, and ρ

completely arbitrary, there is no relationship between the two particles.

A. Zee, Fearful Symmetry.

I.10. Symmetry | 77

Figure I.10.1

It is almost an article of faith among theoretical physicists, enunciated forcefully by

Einstein among others, that the fundamental laws should be orderly and simple, rather

than arbitrary and complicated. This orderliness is reflected in the symmetry of the action.

Suppose that m

and λ

=λ

; then the two particles would have the same mass and

their interaction, with themselves and with each other, would be the same. The Lagrangian

L becomes invariant under the interchange symmetry ϕ

←→ ϕ

Next, suppose we further impose the condition ρ = λ

= λ

so that the Lagrangian

becomes

L =



(∂ϕ

)

+ (∂ϕ

)



−



+ ϕ



−



+ ϕ



(2)

It is now invariant under the 2-dimensional rotation {ϕ

(x) → cos θϕ

(x) + sin θϕ

(x),

(x) →−sin θϕ

(x) + cos θϕ

(x)} with θ an arbitrary angle. We say that the theory

enjoys an “internal” SO(2) symmetry, internal in the sense that the transformation has

nothing to do with spacetime. In contrast to the interchange symmetry ϕ

←→ ϕ

the

transformation depends on the continuous parameter θ, and the corresponding symmetry

is said to be continuous.

We see from this simple example that symmetries exist in hierarchies.

Continuous symmetries

If we stare at the equations of motion (∂

+ m

)ϕ

=−λ ϕ

long enough we see that if

we define J

≡ i(ϕ

∂

− ϕ

∂

), then ∂

= i(ϕ

∂

− ϕ

∂

) = 0 so that J

is a

conserved current. The corresponding charge Q =



, just like electric charge, is

conserved.

Historically, when Heisenberg noticed that the mass of the newly discovered neutron

was almost the same as the mass of a proton, he proposed that if electromagnetism were

somehow turned off there would be an internal symmetry transforming a proton into a

neutron.

An internal symmetry restricts the form of the theory, just as Lorentz invariance restricts

the form of the theory. Generalizing our simple example, we could construct a field theory

containing N scalar fields ϕ

, with a =1,

...

, N such that the theory is invariant under the

transformations ϕ

→R

(repeated indices summed), where the matrix R is an element

of the rotation group SO(N) (see appendix B for a review of group theory). The fields ϕ

transform as a vector ϕ = (ϕ

...

, ϕ

). We can form only one basic invariant, namely the

78 | I. Motivation and Foundation

⫺2i␭(␦

␦

⫹ ␦

␦

⫹ ␦

␦

)

Figure I.10.2

scalar product ϕ

ϕ = ϕ

=ϕ

(as always, repeated indices are summed unless otherwise

specified). The Lagrangian is thus restricted to have the form

L =



(∂ ϕ)

− m

ϕ



−

( ϕ

)

(3)

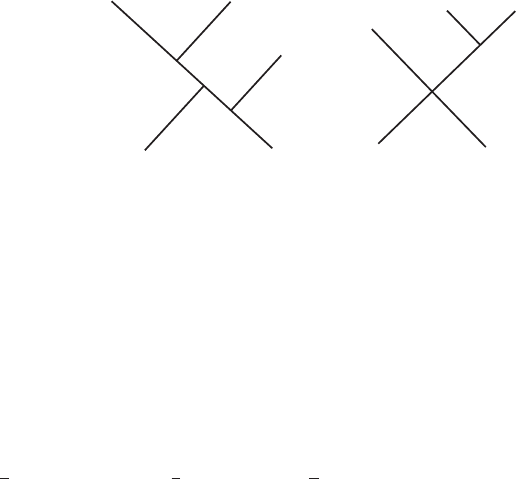
The Feynman rules are given in fig. I.10.2. When we draw Feynman diagrams, each line

carries an internal index in addition to momentum.

Symmetry manifests itself in physical amplitudes. For example, imagine calculating

the propagator iD

(x) =



D ϕe

(x)ϕ

(0). We assume that the measure D ϕ is in-

variant under SO(N ). By thinking about how D

(x) transforms under the symmetry

group SO(N ) you see easily (exercise I.10.2) that it must be proportional to δ

. You can

check this by drawing a few Feynman diagrams or by considering an ordinary integral



d qe

−S(q)

. No matter how complicated a diagram you draw (fig. I.10.3, e.g.) you al-

ways get this factor of δ

. Similarly, scattering amplitudes must also exhibit the symmetry.

Without the SO(N) symmetry, many other terms would be possible (e.g., ϕ

for

some arbitrary choice of a, b, c, and d) in (3).

We can write R =e

where θ

T =



is a real antisymmetric matrix. The group

SO(N ) has N(N − 1)/2 generators, which we denote by T

. [Think of the familiar case of

SO(3).] Under an infinitesimal transformation (repeated indices summed) ϕ

→R



(1 + θ

)

, or in other words, we have the infinitesimal change δϕ

= θ

Noether’s theorem

We now come to one of the most profound observations in theoretical physics, namely

Noether’s theorem, which states that a conserved current is associated with each generator

Figure I.10.3

I.10. Symmetry | 79

of a continuous symmetry. The appearance of a conserved current for (2) is not an acci-

dent.

As is often the case with the most important theorems, the proof of Noether’s theorem is

astonishingly simple. Denote the fields in our theory generically by ϕ

a .

Since the symmetry

is continuous, we can consider an infinitesimal change δϕ

. Since L does not change,

we have

0 = δL =

δL

δϕ

δL

δ∂

δL

δϕ

δL

δ∂

∂

δϕ

(4)

We would have been stuck at this point, but if we use the equations of motion δL/δϕ

∂

(δL/δ∂

) we can combine the two terms and obtain

0 = ∂



δL

δ∂

δϕ



(5)

If we define

≡

δL

δ∂

δϕ

(6)

then (5) says that ∂

= 0. We have found a conserved current! [It is clear from the

derivation that the repeated index a is summed in (6)].

Let us immediately illustrate with the simple scalar field theory in (3). Plugging δϕ

)

into (6) and noting that θ

is arbitrary, we obtain N(N − 1)/2 conserved

currents J

= ∂

)

, one for each generator of the symmetry group SO(N).

In the special case N =2, we can define a complex field ϕ ≡ (ϕ

+ iϕ

√

2. The La-

grangian in (3) can be written as

L = ∂ϕ

†

∂ϕ − m

†

ϕ − λ(ϕ

†

ϕ)

and is clearly invariant under ϕ → e

iθ

ϕ and ϕ

†

→ e

−iθ

†

. We find from (6) that J

i(ϕ

†

∂

ϕ − ∂

†

ϕ), the current we met already in chapter I.8. Mathematically, this is

because the groups SO(2) and U(1) are isomorphic (see appendix B).

For pedagogical clarity I have used the example of scalar fields transforming as a vector

under the group SO(N ). Obviously, the preceding discussion holds for an arbitrary group

G with the fields ϕ transforming under an arbitrary representation R of G. The conserved

currents are still given by J

= ∂

)

with T

the generators evaluated in the

representation R. For example, if ϕ transform as the 5-dimensional representation of

SO(3) then T

isa5by5matrix.

For physics to be invariant under a group of transformations it is only necessary that the

action be invariant. The Lagrangian density L could very well change by a total divergence:

δL = ∂

, provided that the relevant boundary term could be dropped. Then we would

see immediately from (5) that all we have to do to obtain a formula for the conserved

current is to modify (6) to J

≡ (δL/δ∂

)δϕ

− K

. As we will see in chapter VIII.4,

many supersymmetric field theories are of this type.

80 | I. Motivation and Foundation

Charge as generators

Using the canonical formalism of chapter I.8, we can derive an elegant result for the charge

associated with the conserved current

Q ≡



δL

δ∂

δϕ

Note that Q does not depend on the time at which the integral is evaluated:



x∂

=−



x∂

= 0 (7)

Recognizing that δL/δ∂

is just the canonical momentum conjugate to the field ϕ

,we

see that

i[Q, ϕ

] =δϕ

(8)

The charge operator generates the corresponding transformation on the fields. An impor-

tant special case is for the complex field ϕ in SO(2)  U(1) theory we discussed; then

[Q, ϕ] = ϕ and e

iθQ

ϕe

−iθQ

= e

iθ

ϕ.

Exercises

I.10.1 Some authors prefer the following more elaborate formulation of Noether’s theorem. Suppose that the

action does not change under an infinitesimal transformation δϕ

(x) = θ

[with θ

some parameters

labeled by A and V

some function of the fields ϕ

(x) and possibly also of their first derivatives with

respect to x]. It is important to emphasize that when we say the action S does not change we are not

allowed to use the equations of motion. After all, the Euler-Lagrange equations of motion follow from

demanding that δS = 0 for any variation δϕ

subject to certain boundary conditions. Our scalar field

theory example nicely illustrates this point, which is confused in some books: δS = 0 merely because S

is constructed using the scalar product of O(N) vectors.

Now let us do something apparently a bit strange. Let us consider the infinitesimal change written

above but with the parameters θ

dependent on x . In other words, we now consider δϕ

(x) = θ

(x)V

Then of course there is no reason for δS to vanish; but, on the other hand, we know that since δS does

vanish when θ

is constant, δS must have the form δS =



(x)∂

(x). In practice, this gives us

a quick way of reading off the current J

(x); it is just the coefficient of ∂

(x) in δS.

Show how all this works for the Lagrangian in (3).

I.10.2 Show that D

(x) must be proportional to δ

as stated in the text.

I.10.3 Write the Lagrangian for an SO(3) invariant theory containing a Lorentz scalar field ϕ transforming

in the 5-dimensional representation up to quartic terms. [Hint: It is convenient to write ϕ as a 3 by 3

symmetric traceless matrix.]

I.10.4 Add a Lorentz scalar field η transforming as a vector under SO(3) to the Lagrangian in exercise I.10.3,

maintaining SO(3) invariance. Determine the Noether currents in this theory. Using the equations of

motion, check that the currents are conserved.

I.11 Field Theory in Curved Spacetime

General coordinate transformation

In Einstein’s theory of gravity, the invariant Minkowskian spacetime interval ds

μν

= (dt)

− (d x)

is replaced by ds

= g

μν

, where the metric tensor

μν

(x) is a function of the spacetime coordinates x. The guiding principle, known as the

principle of general covariance, states that physics, as embodied in the action S , must be

invariant under arbitrary coordinate transformations x → x



(x). More precisely, the prin-

ciple

states that with suitable restrictions the effect of a gravitational field is equivalent to

that of a coordinate transformation.

Since

= g



λσ

λ

σ

= g



λσ

∂x

λ

∂x

σ

∂x

= g

μν

the metric transforms as



λσ



)

∂x

λ

∂x

σ

∂x

= g

μν

(x) (1)

The inverse of the metric g

μν

is defined by g

μν

νρ

= δ

A scalar field by its very name does not transform: ϕ(x) = ϕ



). The gradient of the

scalar field transforms as

∂

ϕ(x) =

∂x

λ

∂x

∂ϕ



)

∂x

λ

∂x

λ

∂x

∂



)

By definition, a (covariant) vector field transforms as

(x) =

∂x

λ

∂x



)

For a precise statement of the principle of general covariance, see S. Weinberg, Gravitation and Cosmology,

p. 92.