Загряцкий Н.И. Управленческий анализ в отраслях

Подождите немного. Документ загружается.

Средняя величина обобщает качественно однородные значения признака

и, следовательно, служит типичной характеристикой признака в данной

совокупности. Средняя величина не фиксирована раз и навсегда: средняя

выработка на одного сотрудника нормально функционирующего предприятия

растет, средние затраты на единицу продукции с ростом объема выпуска

обычно падают. Таким образом, не только сами средние значения величин, но

тенденции их изменения можно рассматривать в качестве индикаторов

положения предприятия на рынке и успешности его финансово-хозяйственной

деятельности.

Существует несколько видов средних величин. Наиболее простой и

прозрачный смысл имеет

средняя арифметическая.

Формула для расчета средней арифметической:

xxx

∑

+++

121

...

Так вычисляют среднюю величину, если общий признак в совокупности

распределяется поровну между всеми единицами. Если же объем совокупности

представляет собой ряд распределения, используют значение

средневзвешенной

арифметической средней.

Формулу ее расчета иллюстрирует следующий

пример.

Пример. Молокозавод выпускает сметану различной жирности, реализуя

ее по разной цене. Данные о реализации разных сортов сметаны за неделю

представлены ниже.

Цена, руб./кг

30,60 32,0 33,10 35,20 Итого

Объем реализации, кг

450 391 406 350 1597

Средневзвешенная средняя арифметическая цена одного килограмма

сметаны, реализованной за неделю составила

∑

350406391450

3502.354061.33391324506.30

⋅

+⋅

=32,6 руб.

Средняя геометрическая величина позволяет сохранять неизменным не

сумму, а произведение индивидуальных значений величин

nгеом

xxxx ...

⋅⋅= .

Основное применение средняя геометрическая находит при изучении

темпов роста.

Пример. Темпы роста цен на сырье, используемое в производстве

продукции предприятия, в течение четырех кварталов текущего года составили

Квартал I II III IV

Темп роста 1.05 1.09 2.01 1.56,

тогда квартальный темп роста цен в среднем за год равен

38,156,101,209,105,1

=⋅⋅⋅ .

Еще один показатель, характеризующий средние величины –

средняя

гармоническая.

Он используется в случаях, когда необходимо, чтобы при

усреднении оставалась неизменной сумма величин, обратных индивидуальным

значениям признака. Формула расчета средней гармонической такова

∑

гарм

Пример. Рабочий изготавливает на станке 520 деталей за дневную смену, в

ночную смену его выработка составляет 450 деталей. Если дневная и ночная

смены равны по продолжительности, то среднесменная выработка на одного

рабочего составит

50,482

450

520

гарм

Между приведенными видами средних величин существует следующее

соотношение

xxx

геомгарм

≤≤

В управленческом анализе широко используется также

средняя

хронологическая.

Для характеристики предприятия применяются интервальные

и моментные показатели. Параметрами первых являются товарооборот,

прибыль, объем поступления за некоторый период; примерами вторых –

данные о запасах, основных средствах, численность работающих на

определенную дату. Для усреднения интервальных показателей чаще всего

привлекается формула средней арифметической, а для усреднения моментных

показателей – формула средней хронологической.

Если дан

ряд моментных показателей: х1,…,хn, то средняя

хронологическая

Sch для этого ряда рассчитывается по формуле

Sch= )

...

(

++++

−

Пример. Требуется найти величину среднего товарного запаса в прошлом

году, если имеются следующие данные о запасах (тыс. руб.)

1 января 1 апреля 1 июля 1 октября 1 января

текущего

года

Запас 100 120 111 140 106

Пользуясь формулой средней хронологической, находим

Sch= 50,118)

106

140111120

100

(

=++++ тыс. руб.

Экономическая интерпретация полученной величины такова: в течение

прошлого года предприятие ежеквартально имело запас товаров, равный в

среднем 118,50 тыс. руб.

Метод группировки – это расчленение совокупности данных на группы с

целью изучения ее структуры или взаимосвязей между компонентами. В

процессе группировки единицы совокупности распределяются по группам в

соответствии со следующим принципом: различие между единицами,

отнесенными к одной группе, должно быть меньше, чем различие между

единицами, отнесенными к разным группам.

Важнейший вопрос при проведении такого рода исследования – выбор

интервала группировки. Существует два основных подхода к его решению.

Первый подход предполагает деление совокупности данных на группы с

равными интервалами значений. Данный подход используют наиболее часто,

т.к. он лишен субъективизма при выборе границ интервалов. При определении

длины интервала

i применяют формулу Стерджеса:

minmaxminmax

lg32.31

−

где

max

и X

min

– соответственно максимальное и минимальное значение

признака в изучаемой совокупности;

К – число групп или интервалов, на которое разбивается исходная

совокупность;

N – число наблюдений.

Согласно

второму подходу интервалы группировки выбирают неравными

(возрастающими или убывающими). Такой подход обычно применяют при

большой неравномерности распределения признака по всему интервалу его

изменения, и интервалы выбирают таким образом, чтобы группы были

равнозаполненными.

Пример. Компания «Фарма» владеет сетью стационарных аптек, аптечных

киосков на улице и в магазинах, фармацевтических отделов в различных

магазинах города (К=4). Выручка 35 торговых точек, принадлежащих

компании, за июль текущего года составила (тыс. руб)

597 670 412 456 880 978 536

372 530 918 417 817 514 431

150 481 672 327 451 352 470

178 379 184 484 314 657 648

205 315 227 219 890 772 690

На основании формулы Стерджеса получим

20.135

35lg32.31

150978

⋅+

−

Округлив этот результат, в качестве длины интервала группировки

выберем 140, тогда группировка имеет вид

Интервал

группировки

150-350 350-550 550-750 750 и более

Количество

единиц

9 14 7 5

Если применим подход равнозаполненных интервалов разной длины, то

такая группировка выглядит следующим образом:

Интервал

группировки

100-300 300-380 380-480 480-600 600-740 740 и

более

количество

единиц в

группе

6 6 6 6 6 5

В подобной группировке интервалы, начиная со второго, постоянно

увеличиваются.

Мощным орудием управленческого анализа является

индексный метод.

Индекс – это статистический показатель, представляющий отношение двух

состояний какого-либо признака. С помощью индексов проводятся сравнения с

планом, в динамике, в пространстве. Индекс называется

простым (частным,

индивидуальным), если исследуемый признак берется без учета связи его с

другими признаками изучаемых явлений. Простой индекс имеет вид

где

и p

– сравниваемые состояния признака.

Пример. Себестоимость единицы продукции в прошлом году составила

200 руб., а в отчетном году – 182,5 руб. Тогда индекс изменения себестоимости

в динамике

912,0

200

50,182

т.е. себестоимость снизилась на 8,8 %.

Индекс называется

аналитическим (общим, агрегатным), если

исследуемый признак берется не изолированно, а в связи с другими

признаками. Аналитический индекс всегда состоит из двух компонентов:

индексируемого признака

Р, динамика которого исследуется, и весового

признака

q. С помощью признака – весов измеряется динамика сложного эко-

номического явления, отдельные элементы которого несоизмеримы. Простые и

аналитические индексы дополняют друг друга.

Применяются аналитический индекс Э. Ласпейрса

∑

и аналитический индекс Г. Пааше

∑

В обоих аналитических индексах q выступает как коэффициент

соизмерения. В 1-м индексе

q взято на уровне предыдущего периода, а во 2-м –

на уровне текущего периода, следовательно, результаты расчетов индексов по

приведенным формулам будут неодинаковы. Поэтому применяют средний

геометрический индекс.

Пример. Индекс Ласпейрса показал, что среднее изменение цен на три

вида материалов составило 1,01, а индекс Пааше – 0,98. Средний

геометрический индекс

995,098,001,1 =⋅ .

Изменения результатов деятельности хозяйствующего субъекта

происходят вследствие взаимодействия сложной системы взаимосвязанных и

взаимообусловленных факторов. Поэтому возникает необходимость в

применении статистико-экономических методов, позволяющих выявить

закономерности изменений в динамике, установить общие тенденции, дать

прогноз на перспективу.

Наибольшее распространение в практике получили корреляционный,

регрессионный, дисперсионный методы анализа. В последние годы стали

привлекать

компонентный, кластерный методы современного анализа.

Корреляционный анализ есть метод установления связи и измерения ее

тесноты между наблюдениями, которые можно считать случайными и

выбранными из совокупности распределенной по многомерному нормальному

закону. Различают связь прямую, когда с ростом (снижением) значений

факторного показателя наблюдается тенденция к росту (снижению) значений

результативного показателя. В противном случае между показателями

существует обратная связь.

статистике теснота связи определяется с помощью различных

коэффициентов (Фехнера, Пирсона, коэффициента ассоциации и т.д.), а в

управленческом анализе чаще используется линейный коэффициент

корреляции.

Коэффициент корреляции между факторами

Х и У определяется по

формуле

[]

2/1

)()(

))((

∑∑

∑

−⋅−

−−

yyxx

где

х,у – значения факторного и результативного показателя соответственно;

yx, - среднее значение соответствующих показателей.

Значение коэффициента корреляции изменяется в интервале (-1,+1).

Значение

r = -1 свидетельствует о наличии жестко детерминированной обратно

пропорциональной связи между показателями,

r = +1 соответствует жестко

детерминированной связи с прямо пропорциональной зависимостью

показателей. Если линейной связи между показателями не наблюдается,

≈

r .

Другие значения коэффициента корреляции характеризуют наличие

стохастической связи, причем чем ближе

r к единице, тем связь теснее.

При

<0,3 связь можно считать слабой, при 0,3<

<0,7 – связь средней

тесноты, при

>0,7 – связь тесная.

Регрессионный анализ – это метод установления аналитического

выражения стохастической зависимости между исследуемыми признаками.

Уравнение регрессии показывает, как в среднем изменяется

у при изменении

любого из

, и имеет вид

xxxfy ,...,,(

где у – зависимая переменная;

– независимые переменные (факторы).

Если независимая переменная одна – это простой регрессионный анализ,

если же их несколько (

n≥2), то такой анализ называется многофакторным.

Применяется регрессионный анализ главным образом для планирования, а

также для разработки нормативной базы.

В отличие от корреляционного анализа, который отвечает на вопрос,

существует ли связь между анализируемыми признаками, регрессионный

анализ дает ее формализованное выражение. Кроме того, если корреляционный

анализ изучает любую взаимосвязь факторов, то регрессионный

анализ –

одностороннюю зависимость, т.е. связь, показывающую, каким образом

изменение факторных признаков влияет на результативный признак.

Регрессионная модель может быть при наличии любой зависимости,

однако в многофакторном анализе используют только линейные модели вида

xbxbxbay

++= ...

2211

Построение уравнения регрессии осуществляют, как правило, методом

наименьших квадратов, суть которого состоит в минимизации суммы квадратов

отклонений фактических значений результативного признака

от его

расчетных значений, т.е.:

∑

→−=

yyS

min)( ,

где

m – число наблюдений;

xbxbxbay ++++= ...

- расчетное значение результа-

тивного фактора.

Коэффициенты регрессии рекомендуется определять с помощью пакетов

программ, реализуемых на персональном компьютере.

1.1.4. Линейное программирование

Задачи, которые решаются на основе методов линейного

программирования, широко распространены в производстве (задача

рациональной загрузки производственных мощностей, научное управление

материальными запасами), на транспорте (задача планирования транспортных

потоков, задача о назначениях и распределении работ), в сельском хозяйстве

(оптимизация использования капитальных вложений и минеральных

удобрений) и т.д.

Задача линейного программирования в

общем случае включает три

компоненты (целевую функцию

F, ограничения и граничные условия) и имеет

следующую математическую постановку:

∑∑

→=

ijij

xcF

min(max) ;

∑

=≤

iij

mjax

,1; ;

∑

=≤

jij

nibx

,1; ;

0≥

x .

Где

i – номер (индекс) поставщика (i=1,2,…,n);

j– номер (индекс) потребителя (j=1,2,…,m);

– транспортные расходы по доставке единицы продукции от i-го

поставщика

j-му потребителю;

– ресурсы, поставляемые i-м поставщиком j-му потребителю; эта

величина неизвестна и подлежит определению;

– запасы каждого поставщика;

– заявки каждого потребителя.

Целевая функция в общем случае оценивает как желательные свойства

для хозяйствующего субъекта (например, прибыль, производительность), так и

нежелательные для него (затраты, простои оборудования и др.). Если требуется

максимизировать какое-то свойство (к примеру, прибыль), то в результате

решения задачи данный критерий (прибыль) будет иметь наибольшее значение

из всех допустимых решений. Если же

требуется минимизировать целевую

функцию (стоимость, расход материалов, время простоев оборудования), то в

результате решения критерий будет иметь наименьшее значение из всех

допустимых.

Ограничения обычно выражают определенные зависимости между

переменными величинами, которые могут быть теоретическими

(формульными), и статистическими.

Теоретические зависимости обычно

справедливы при любых условиях, и для их получения не требуется никаких

дополнительных измерений. Однако на практике достаточно часто между

параметрами модели нет функциональной зависимости. Так, например, если мы

желаем оптимизировать использование общественного транспорта города в

течение суток, то нам необходимо знать, как пассажиропоток распределен во

времени. Естественно, что

такой готовой зависимости нет, и для ее получения

потребуется осуществить сбор и обработку статистических данных, чтобы

получить определенную аналитическую зависимость, которая и будет тем

ограничением, которое следует включить в задачу линейного

программирования.

Граничные условия показывают предельно допустимые значения

искомых переменных, и в общем случае они могут быть двусторонними, типа

jiji

bxа ≤≤ . Обычно искомые величины являются положительными или

равными нулю, и накладывается только требование неотрицательности

0≥

x .

Решение реальных задач линейного программирования со многими

переменными и ограничениями связано с очень большими объемами

вычислений, поэтому без применения ЭВМ и прикладных программ поиск

оптимального решения практически невозможен.

1.2. Маржинальный анализ

1.2.1. Основные положения маржинального анализа

Маржинальный анализ базируется на группировке затрат на переменные,

т.е. изменяющиеся по мере увеличения или уменьшения объема производства,

и постоянные, не зависящие от объема производства, и на выведении

маржинального дохода.

Следует иметь в виду, что понятия «постоянные» и «переменные»

относятся к суммарным затратам, а не к затратам на единицу продукции.

Применительно

к удельным затратам наблюдается обратная картина: при

изменении объема производства постоянные затраты изменяются, а

переменные остаются без изменений.

Структура отчетов о доходах при такой группировке представляет собой

следующее:

Объем продаж.

Переменные затраты.

Маржинальный доход (п. 1-2)

Постоянные затраты.

Операционная прибыль (прибыль от продаж) (п. 3-4).

Таким образом, в отчете содержатся два финансовых показателя:

маржинальный доход и прибыль.

Маржинальный доход представляет собой сумму денежных средств,

необходимых для покрытия постоянных затрат и образования прибыли, и

равняется разности между объемом продаж и переменными затратами на

производство и реализацию продукции. Для решения ряда задач

можно также

рассматривать маржинальный доход как сумму постоянных затрат и прибыли.

Выделение в отчете о доходах такого финансового показателя, как

маржинальный доход, позволяет выяснить, является ли выпускаемая продукция

рентабельной. Поскольку постоянные затраты представлены отдельной

строкой, четко видно их влияние на формирование операционной прибыли

(прибыль от продаж). Покажем аналитические возможности такого

представления информации о затратах и доходах, которое называют также

маржинальным подходом, на условном примере.

Пример. Допустим, рассматривается информация о результатах работы

предприятия за определенный период, согласно которой объем продаж

составил 20 млн руб., а полная себестоимость продаж – 25 млн руб. В этом

случае делается вывод о том, что продукция убыточна и ее производство

невыгодно.

При использовании маржинального подхода аналитики будут иметь дело

со следующими цифрами:

У понятия «маржинальный доход» имеются такие синонимы, как «сумма покрытия», «валовая

прибыль», «контрибуция».

• объем продаж – 20 млн руб.;

• переменные затраты – 12 млн руб.;

• маржинальный доход – 8 млн руб.;

• постоянные затраты – 13 млн руб.;

• операционная прибыль – 5 млн руб.

Приведенные цифры показывают, что предприятие получает доход от

производства и реализации продукции в сумме 8 млн руб., т.е. продукция

рентабельна. Однако постоянные затраты, связанные с функционированием

предприятия, несоразмерно велики, что и приводит к убытку. Очевидно, что

для устранения убыточности необходимо либо увеличивать маржинальный

доход, либо снижать постоянные

затраты, либо пытаться одновременно решать

обе эти задачи. Например, маржинальный доход можно увеличить за счет

повышения цен, снижения переменных затрат, увеличения физического объема

продаж и т.д. Таким образом, возможности для анализа и принятия

последующих решений принципиально возрастают.

С известной долей условности можно выделить следующие этапы

(направления) маржинального анализа:

• анализ безубыточности;

• анализ соотношения «затраты – объем продаж – прибыль»;

• анализ на основе деления затрат на релевантные и нерелевантные.

1.2.2. Анализ безубыточности

Центральным моментом анализа безубыточности (равновесного анализа)

является определение точки безубыточности (точки равновесия), т.е. такого

объема продаж, при котором выручка от реализации продукции (работ, услуг)

равняется сумме всех затрат. Очевидным при этом является то, что превышение

данного объема обеспечивает получение прибыли во все возрастающих

масштабах, а его уменьшение – убытка.

Основными методами

анализа безубыточности являются балансовый,

маржинальный и графический.

При

балансовом методе исходят из следующей зависимости:

П=px – (А+вх), (1.1)

где

П – прибыль от продаж; р – продажная цена единицы продукции; х –

количество единиц продукции, которое необходимо продать для достижения

точки равновесия;

А – сумма постоянных затрат; в – переменные затраты на

единицу продукции.

Поскольку в точке равновесия прибыль нулевая, формула 1.1. принимает

следующий вид:

рх=А+вх. (1.2)

Предположим, что продажная цена единицы продукции – 200 тыс. руб.,

сумма постоянных затрат – 15 млн руб., переменные затраты на единицу

продукции – 50 тыс. руб.

Точка равновесия определится из уравнения 1.2:

200

х=15000+50х,

х=100 единиц.

Маржинальный метод анализа предполагает, что каждая проданная

единица продукции обеспечивает получение определенного маржинального

дохода (удельного маржинального дохода), который в первую очередь идет на

покрытие постоянных затрат, а затем – на формирование прибыли. Иначе

говоря, для достижения точки безубыточности необходимо реализовать такое

количество единиц продукции, которое обеспечит сумму удельных

маржинальных доходов, равную величине постоянных

затрат. Таким образом,

для нахождения точки безубыточности следует сумму постоянных затрат

разделить на удельный маржинальный доход. Эту зависимость можно также

получить, преобразуя формулу 1.2, из которой следует:

вр

−

= (1.3)

В рассматриваемом примере величина удельного маржинального дохода

составляет 150 тыс. руб. (200 тыс. – 50 тыс.).

Точка безубыточности соответственно равна:

15000:150=100 единиц.

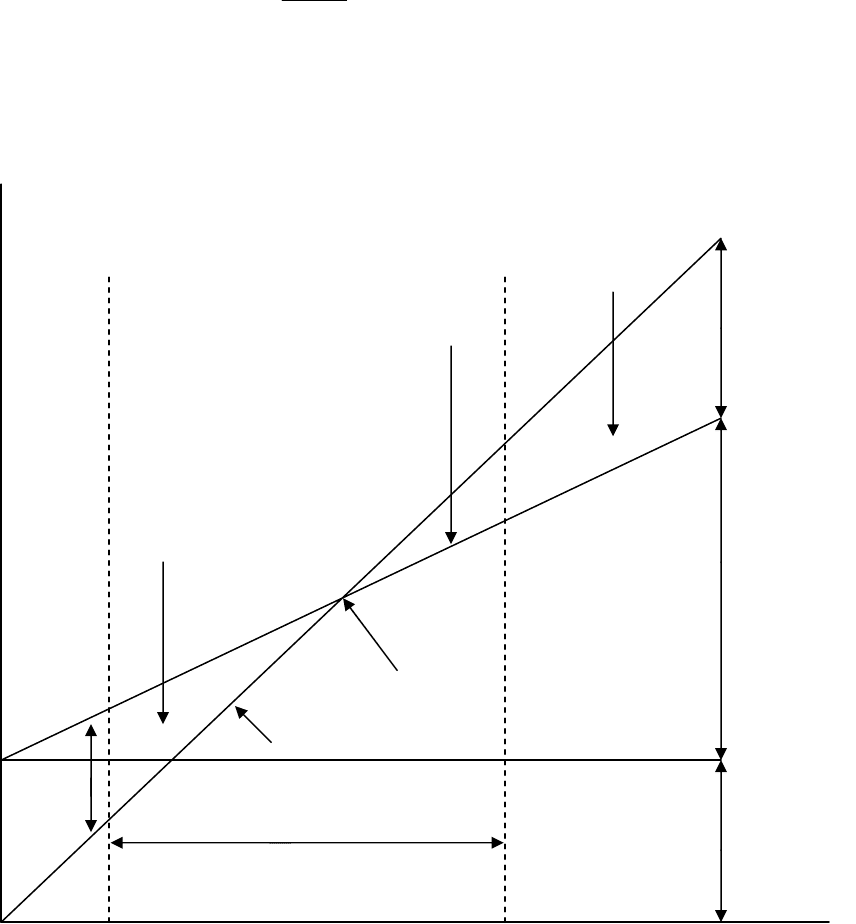
Область прибылей

Прибыль

Совокупные затраты

Переменные

Область убытков затраты

Точка безубыточности

Выручка

убыток Приемлемый диапазон

объемов производства

Объем производства (продаж) в единицах продукции

Рис. 1.2. График безубыточности

Графический метод (рис. 1.2) имеет то преимущество, что дает наглядное

представление о том, как будут изменяться затраты и прибыль для многих

Зат

аты и п

ажи

ру

б.

Посто-

янные

затраты