Юрганов А.А., Кожевников В.А. Регулирование возбуждения синхронных генераторов

Подождите немного. Документ загружается.

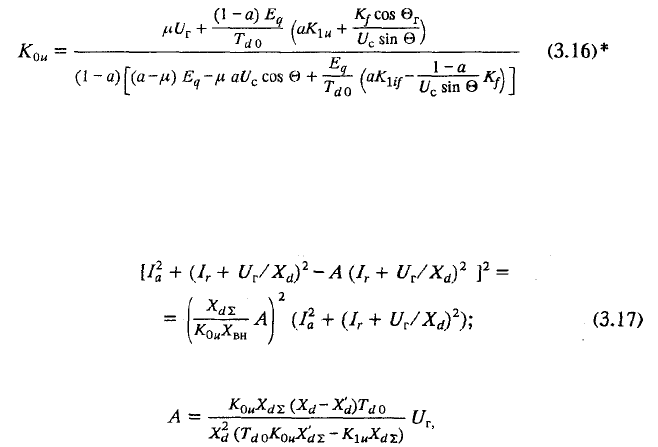
Таким образом, при реальных значениях коэффициента К

область

апериодической устойчивости при перевозбуждении (Q > 0)

ограничена справа режимами, в которых угол между Е

и U

достигает

90°. При реальных значениях 0.2 ≤ Х

вн

≤ 0.5 о. е. это ограничение

лежит намного правее области допустимых режимов и его можно не

учитывать. В режимах потребления реактивной мощности (Q < 0)

апериодическая устойчивость нарушается при превышении

внутренним углом между Е

и U

значения 90°. Эта левая граница

существенно ограничивает область устойчивых рабочих режимов.

Однако при конечных значениях K

устойчивы режимы, лежащие

левее прямой I

=-U

, которую до сих пор всегда считали пределом

апериодической устойчивости синхронной машины обычного

исполнения в режимах потребления [9 ]. Расширение области тем

больше, чем меньше величина К

. Поэтому с точки зрения апе-

риодической устойчивости целесообразно снижение этого коэффи-

циента.

3.1.2. Границы электромеханической

колебательной устойчивости

Выражение для максимально допустимого по условиям ус-

тойчивости низкочастотного внешнего электромеханического движе-

ния коэффициента усиления по напряжению

накладывает дополнительные ограничения на область допустимых

режимов. Оно было получено при допущении о безынерционности

каналов регулирования регулятора.

Рассмотрим сначала случай регулирования только по отклонению

напряжения и его производной (K

1if

= K

= 0).

После ряда преобразований (3.16) приводится к виду

где

математически описывающему кривую, получившую название

«улитки» [35 ]. После замены переменных I

=X интересующее

нас решение уравнения 4-й степени получим в виде

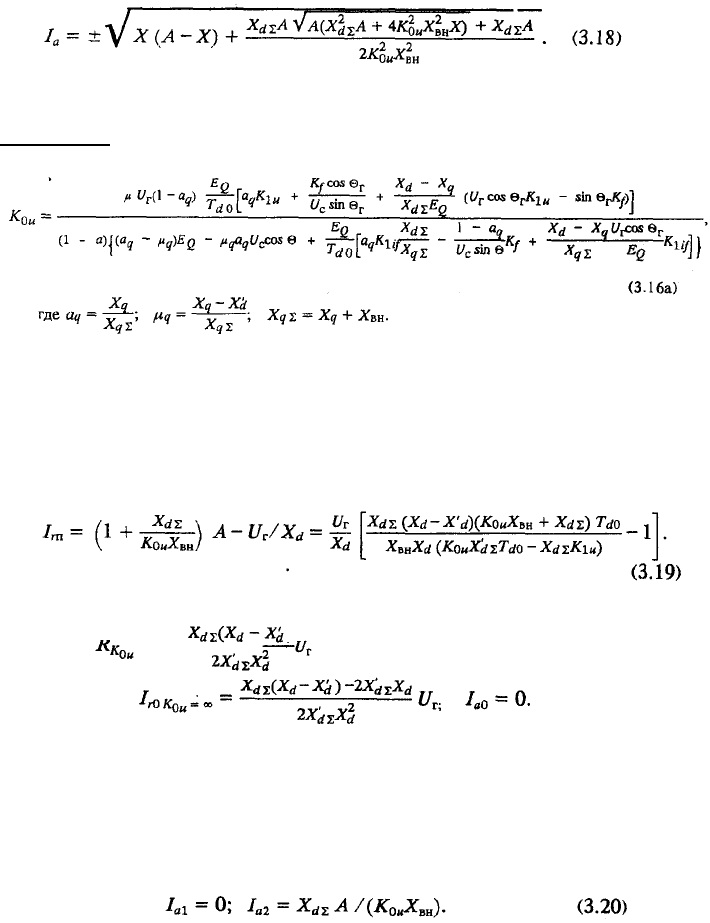
Знак «плюс» соответствует генераторному режиму, знак «минус»

— двигательному.

* Для гидрогенератора выражение (3.16) имеет вид:

Нетрудно заметить, что при X

= X

(турбогенератор) оно полностью совпадает с

(3.16).

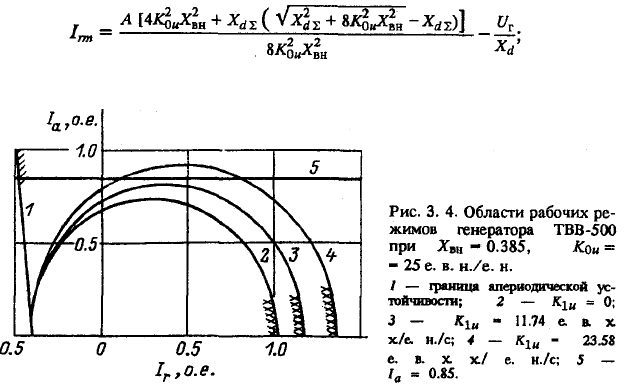
На рис. 3.4 приведены границы колебательной устойчивости при

= 25 e.в.н./е.н. для трех различных значений K

, а на рис. 3.5 — то

же при К

= 5 е.в.н./е.н. Видно, что все они пересекают ось абсцисс

слева в точке I

rл

=-U

, а правая точка пересечения I

rп

, зависит от

величины коэффициентов К

и К

При К

→∞ уравнение границы вырождается в окружность (3.8)

радиуса с центром в точке

Построение границы колебательной устойчивости по уравнению

(3.18) требует применения вычислительной техники и специализи-

рованных программ. Поэтому для инженеров, не располагающих ими,

можно предложить предельно простой способ построения границы по

четырем точкам.

Из (3.17) следует, что значению Х = 0 (I

=-U

) соответствуют

два значения активного тока:

При I

0 определяется третья точка (3.19). Четвертую точку

(экстремум) кривой найдем, взяв частную производную выражения

(3.18) по реактивному току

I 

и приравняв ее нулю:

Нанеся эти четыре точки на диаграмму рабочих режимов и сое-

динив их между собой плавной выпуклой кривой, можно довольно

точно построить границу колебательной устойчивости для простей-

шего закона регулирования возбуждения.

3.1.3. Рекомендации по применению

Полученные выше соотношения дают возможность без

применения специализированных программ нанести на диаграмму

режимов синхронной машины границы апериодической и колеба-

тельной статической устойчивости при регулировании возбуждения

по отклонений и по первой производной напряжения генератора. Ис-

ходными данными служат параметры исследуемого генератора или

эквивалентного генератора станции и значение Х

вн

. Порядок расчетов

1. Выбираются предполагаемые значения коэффициентов усиления

[е.в.х.х./е.н. ] и K

[е.в.х.х./е.н./с].

2. Строится диаграмма допустимых режимов в координатах

- I

3. Выбираются предполагаемые значения уровней напряжения по

концам эквивалентной электропередачи.

4 А. А. Юрганов, В. А. Кожевников

4. Сравнивается выбранное значение К

с величиной X



вн

;

при К

> X



вн

(наиболее часто встречающийся случай)

наносятся на диаграмму границы «справа» по уравнению (3.6) и

«слева» — по уравнению (3.15).

5. Строится по уравнению (3.18) граница колебательной устой-

чивости. Если выполнить полный объем вычислений затруднительно,

то ее построение выполняется приближенно по четырем точкам (3.19)

—(3.21).

В результате получим область рабочих режимов, представляющую

собой внутреннюю часть построенных областей. Анализируя ее (рис.

3.4 и 3.5), можно решить, справится ли пропорциональный регулятор

со стабилизацией всех возможных режимов, следует ли уменьшать

коэффициент усиления по напряжению или предусмотреть сильное

регулирование возбуждения. При этом нужно иметь в виду, что для

обеспечения приличного качества регулирования необходимо иметь

запас устойчивости в каждом из режимов.

Все эти задачи, а также задачу выбора коэффициента K

, обес-

печивающего требуемое значение К

max, можно решать в полуавто-

матическом режиме с помощью ППП «Модель».

3.2. Статическая устойчивость

при включенных каналах стабилизации

Ранее мы получили границы статической устойчивости при

регулировании по отклонению и производной напряжения.

Реализуемый в российских регуляторах закон регулирования (1.19)

включает в себя дополнительно к отклонению и производной

напряжения сигналы стабилизации по производной тока возбуждения,

а также по отклонению и первой производной частоты напряжения

генератора. В разд. 2.3 было показано, что безынерционный сигнал I'

отрицательно сказывается на устойчивости и в реальных регуляторах

вводится его запаздывание. Положим, что W

1if

=1/(1+рτ), τ =0.15с.

Совместное действие каналов стабилизации «по частоте» по-

прежнему будем учитывать безынерционным сигналом Δf

, вводимым

с эквивалентным коэффициентом K

= 0.5K

[е.в.х.х./рад/с ] (К

[дел] =

[дел]).

В этом случае порядок характеристического уравнения повыша-

ется и его коэффициенты имеют вид:

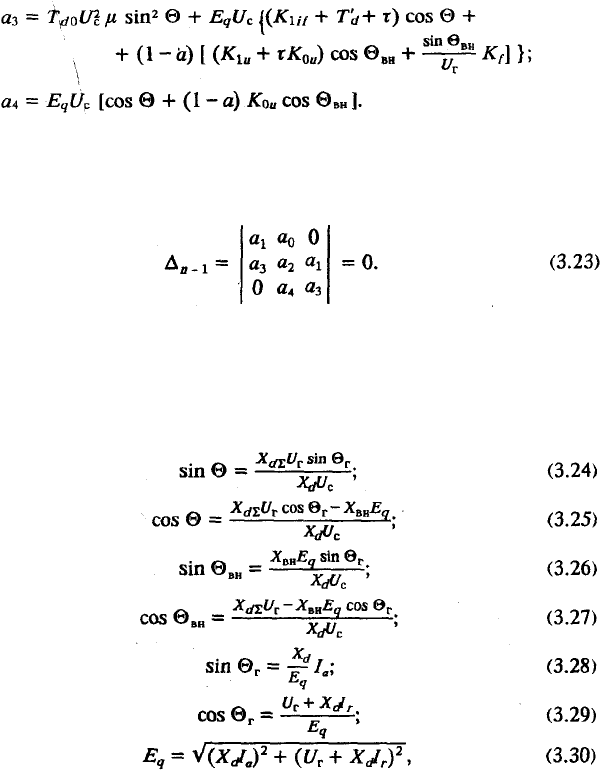
На апериодическую устойчивость каналы производных не влияют.

Ее границы по-прежнему определяются выражениями (3.6), (3.15).

Границу колебательной устойчивости получим, приравняв нулю

предпоследний определитель системы

Аналитическое решение этого уравнения очень громоздко. Поэ-

тому остается только одна возможность: решить его численным ме-

тодом.

Воспользовавшись вытекающими из уравнений установившегося

режима выражениями:

исключим из (3.23) все переменные, кроме активного и

реактивного токов, и получим полное уравнение 9-й степени

относительно I

и I

. Подставив в него параметры электропередачи и

величину напряжения генератора, решим любым численным методом,

например методом Ньютона, и получим для выбранного числа точек

границу в виде зависимости I

). Останется только нанести ее на

область допустимых режимов.

На рис. 3.6—3.8 показано для выбранного расчетного примера, как

влияют сигналы стабилизации по производной тока ротора и частоте

напряжения на области колебательной устойчивости при разной

величине коэффициента усиления по напряжению.

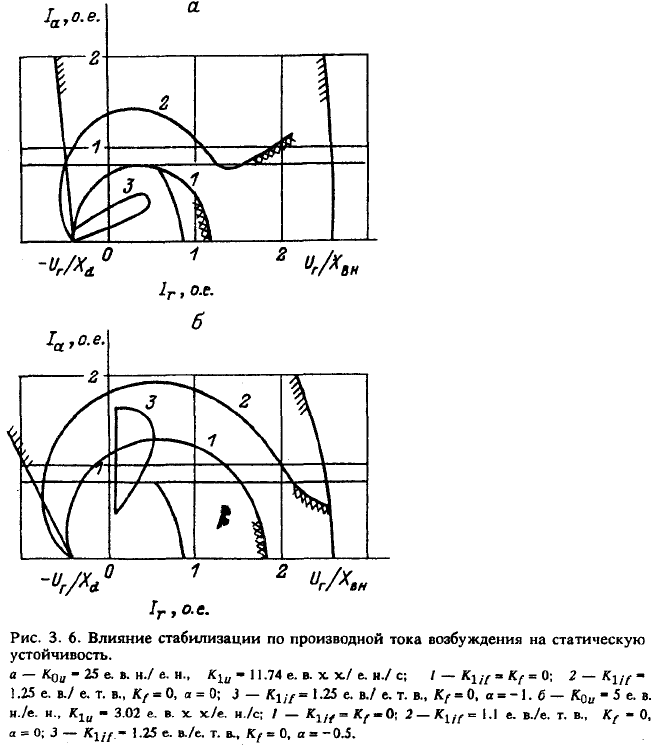
Видно, что стабилизация только «по частоте» расширяет область

устойчивости в режимах перевозбуждения и практически не помогает

в режимах потребления реактивной мощности. Сигнал I'

, наоборот,

помогает в режимах потребления, а в режимах выдачи Q его

эффективность падает. Совместное действие всех каналов стабили-

зации позволяет получить практически одинаковый запас устойчи-

вости в режимах Р = P

ном

, Q = var.

До сих пор мы рассматривали границы устойчивости, то есть ли-

нии нулевого затухания. Однако существует возможность нанести на

область допустимых режимов и линии равного затухания, соответст-

вующие определенной величине вещественной части самой правой

пары комплексных корней системы.