Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


Exercise 101
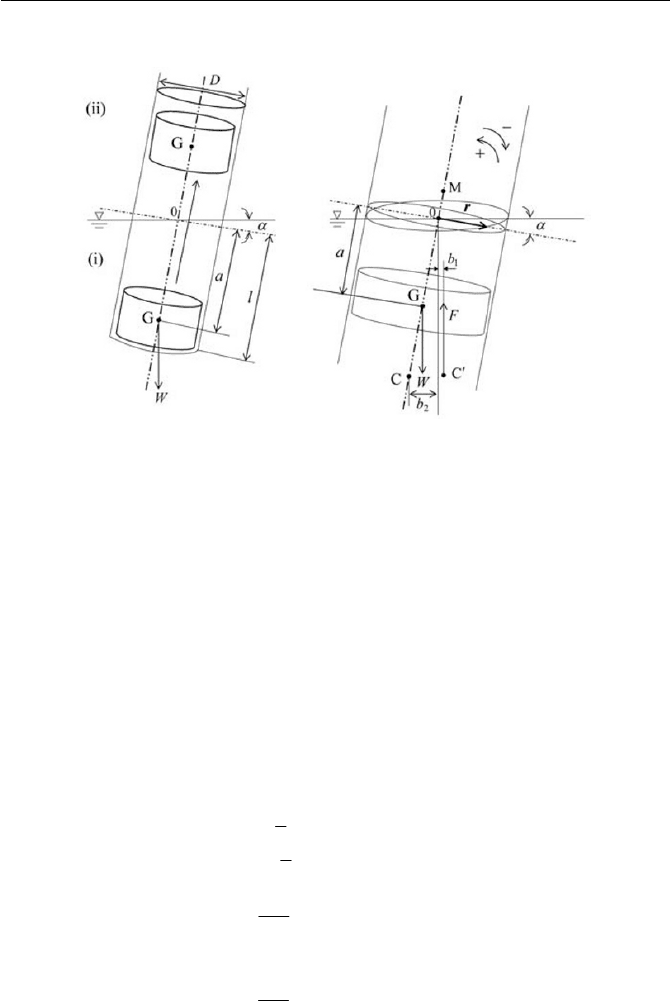
at the axis of rotation
0
acts in a direction such as to restore the object to
its original position, the object is considered to be stable. Contrarily, if the
couple is in the opposite direction and acts to increase the tilt angle, the ob-
ject in this case is unstable. It is quite reasonable to assume for the small
tilt angle that the position of the center of gravity G remains unchanged
with respect to the object, i.e. along the center line of the cylinder, while
the center of buoyancy C takes a new position, as shown in Fig. 3.13(b).
Draw a vertical line from the new center of buoyancy
C
c
so that it inter-
sects the center line of the cylinder at a point
M, called the ‘‘metacenter.’’
The stability of the object thus wholly depends upon the direction of the
couple force due to
F
and W at new position after tilting. In effect, restor-
ing the couple in the tilt position will stabilize the equilibrium if
M
lies
above
G, i.e. the positive couple. On the other hand the equilibrium will be
unstable if M lies below G, i.e. the negative couple.
Now let us calculate
MG , called the metacentric height, and examine
the conditions to determine whether
MG
may be negative or positive.
Suppose, with reference to Fig. 3.13(b), that the center of buoyancy is
shifted from the position
C to C
c
after tilting. The resultant torque (due to
the buoyant force
F
after tilting) should be the sum of the original torque
(due to the buoyant force
F
before tilting) and the contribution of the
buoyancy torque from the elementary prismatic volume around the axis of
rotation
0 as shown in Fig. 3.13(b) due to tilting as follows
012
MFbFb
(1)
2
Fb is the resultant torque about the axis of rotation 0 ,
1
Fb is the origi-
nal torque and
0
M is the torque due to an additional buoyant force caused
by the volume of the displaced fluid. The sign of the torque is negative to
increase the tilting and positive to restore the floating object to its original
position, as shown in Fig. 3.13.
1
b and
2
b are the normal distances to the
buoyant force vector
F
before and after tilting respectively. From Eq. (1)
we have
210
bbFM
(2)
21
bb can be further written as
DDD
GCMGMCMCbb | sin
21
(3)
so that we have
D
GCMGFM
0
(4)
102 3 Fluid Static and Interfaces
(a) (b)
Fig. 3.13 Stability of a tilted object
0
M
in Eq. (4) is the net torque due to the buoyant force in the elementary
prismatic volume, the specific value of which can be obtained by carrying
out following integral
dV
V
g
³
u
U
rM 2
0
(5)
Note that
dV is the volume element at the position of
r
from 0 . Since
the tilting angle
D
is small, gAr can be true, thus Eq. (5) becomes
drdrrM
r
TDU
T
2
0
2
³
,
g
(6)
drdrdV
TD
2
|
, and
³³
¿
¾
½
¯
®
2
2
0
3
0
2
S
S
TDU
ddrrM
R
g
¸
¸
¹
·
¨
¨
©
§
SDU
2
4
R
g
¸
¸
¹
·
¨
¨
©
§
SDU
32
4
D
g
(7)
Exercise 103
S
32
4
DI is the second moment of surface area at the cross section of
the cylinder.
F
is balanced with
W
at equilibrium before tilting, and
F
can
be estimated by
e
VF g
U
(8)
e
V is the displaced volume at equilibrium before tilting. Now it is desir-
able to derive an expression for
MG
, using Eqs. (4), (7) and (8). Thus we
have
GC
F
M
MG
D
0
GC
V
I
e
DU
D
U
g
g
GC
V
I
e
(9)
The couple force
c
W
about 0 is written as
DDW
| MGWMGW
c
sin
(10)
And it follows that
D
DW
MGF
MGW
c
(11)
Therefore, for the stability of the floating object we have the general crite-
ria:
if
0!MG , 0!
c
W
thus stable,
if
0MG , 0
c
W
thus unstable
if
0 MG , 0
c
W
this is meta stable.
For the stability of the floating object in Fig. 3.13(a), we have the fol-
lowing parameters
l
D
V
e
2
2
¸
¹
·
¨
©
§
S
(12)
We can also get
2
l
aGC
(13)
104 3 Fluid Static and Interfaces
Therefore, from Eq. (9),
MG
will be calculated by the following formula
¸
¹
·
¨
©
§
28
2
l
a
l
D
MG
(14)
It is mentioned that l in Eq. (14) can be eliminated from the equilibrium
condition before tilting using following relation
g
US
l
D
W
2
2
¸
¹
·
¨
©
§
(15)
And that is
2
4
D
W
l
SU
g
(16)
From Eqs. (14–16), the stability is given by examining the sign of MG
as the weight is slid upward
28
2
l
l
D
a ; stable
28
2
l
l
D
a ; meta stable
28
2
l
l
D
a !
; unstable
Exercise 3.6 Measurement of Surface Tension
A plate with the dimension of Height
u
Width
u
Depth (a
u
b
u
c) and den-
sity
P
U
is submerged in a liquid
B
at the interface between the air and the
liquid, as shown in Fig. 3.14. The density of the liquid
B
is
B
U
and that of
air is
A
U
. The height of the submerged part of the plate is
B
h from which
the plate is pulled up from the liquid
B
. Determine the surface tension
V
without knowing
A
U
and
B
U
in advance; however, the contact angle
T
is
known.
Ans.
Set the datum force
0
F
before submerging the plate to the liquid
B
.
0
F is the force to hold the plate in the air; i.e.

Exercise 105
BAAP
AP
hhbc
bcabcaF
UU
U
U
g
gg
0
(1)
The second term on the right hand side of Eq. (1) is the net force exerted
by the air, otherwise known as the buoyant force. The force balance when
the plate is submerged in liquid
B
is given by
0 WFFFF
BA
V
(2)
F
is the lift force,
A
F is the net force exerted by the air,
B
F is the buoyant
force of liquid
B
,
V
F is the net force due to surface tension and W is the
weight of the plate. Accordingly, these forces are:
bchF
AAA
g
U
(3)
bchF
BBB
g
U
(4)
>@
T
V
V
cos2 cbF
(5)
bchh
abcW
BAP
P
g
g
U
U
(6)
Thus, from Eqs. (3–6), Eq. (2) gives F as
^`
T
V
U
U
U
U
cos2bchhbcF
BPBAPA
g
(7)
Using
0
F in Eqs. (1–7), we have following relationship
^`
BAB
bchFF
cb
UU
T
V
g
0
cos2
1
(8)
Thus, when the plate is pulled up to position, and when the bottom of
the plate is just lined up with the level of the liquid
B
h
, i.e.
0
B
h
, we can
obtain the surface tension
V
, measuring
F
at 0
B
h
0
cos2
1
FF
cb
T
V
(9)
The contact angle
T
must be measured while the plate is submerged. The
technique to measure the surface tension is called the Wilhelmy plate
method.
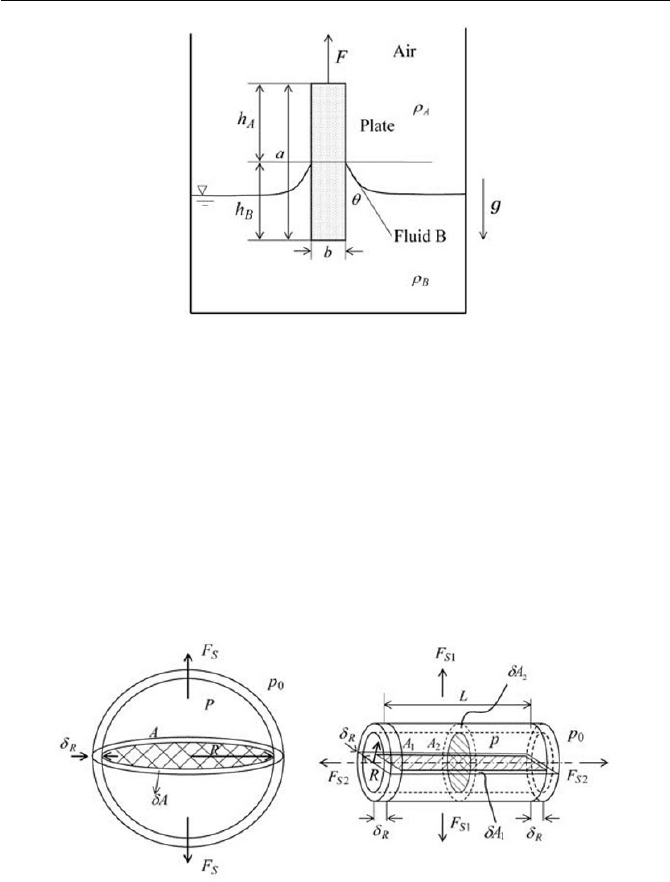
106 3 Fluid Static and Interfaces
Fig. 3.14 The Wilhelmy plate
Exercise 3.7 Pressure vessels
Obtain wall stress of (a) a Spherical tank and (b) a Cylindrical tank, as
shown in Fig. 3.15.
(a) Spherical tank
(b) Cylindrical tank
Fig. 3.15 Pressure vessels

Exercise 107
Ans.
(i) The configuration of the spherical tank is spherically symmetric, so
that force
S
F , which keeps both halves of the sphere apart, is supported by
the cross-sectional area of wall
A
G
. From Eq. (3.1.34),
S
F is obtained by
2
00
RppAppF
S
S
(1)
Thus the stress of the wall
W
W
is
2
2
0
2
R
R
S
W
R
Rpp
A
F
SGGS
S
G
W
(2)
If R
R
G
, the stress
W
W
can be calculated by
R
W
Rpp
G
W
2
0
(3)
(ii) In the case of the cylindrical tank, there are two principle forces acting
on the wall. One is the radial force
1S
F , and another is the axial force
2S
F ,
both of which keep the halves of the tank apart in each direction. Again
from Eq. (3.1.34), the radial force
1S
F is
RLppAppF
S
2
0101
(4)
Thus, the stress of the wall
1W
W
due to
1S
F force can be obtained from
LR
RLppF
RRRA
S
W
u
GGGG
W
2222
2
0
2
1
1
(5)
If
R
R
G
, the stress
1W
W
will become approximately
R
W
LR
RLpp
G
W
2
0
1
(6)
Similarly, the stress of the wall
2W
W
due to the
2S
F force will be
2
2
0
2
2
2
2
R
RA
S
W
R
RppF
SGGS
S
G
W
(7)
If R
R
G
, the
2W
W
becomes approximately
108 3 Fluid Static and Interfaces
R
W
Rpp
G
W
2
0
2
(8)
Eventually it will be the same as the spherical tank case in axial direction.
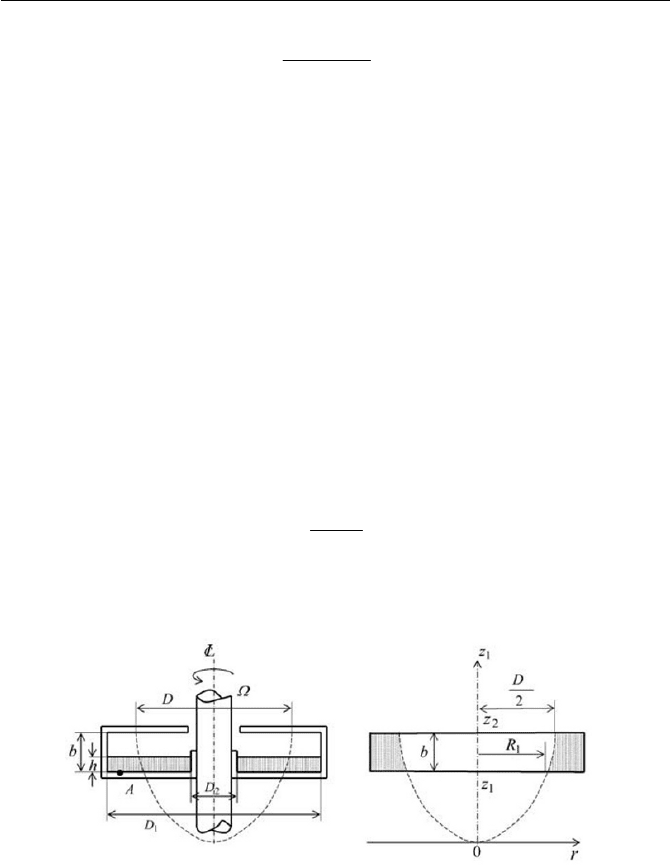
Exercise 3.8 Oil Feeding Reservoir
The cylindrical container shown in Fig. 3.16 is rotated with the shaft about
its centerline. Lubrication oil, whose density is
U
with height h , is en-
closed in the container before rotation. What is the rotational speed neces-
sary for the oil to reach the diameter
D
at the upper wall of the container?
Also, obtain the pressure
A
p
at the lower corner of the container at point A,
when it is rotated at that speed. Note that the container is opened for at-
mospheric pressure
a
p .
Ans.
From Eq. (3.1.41), the profile of the free surface is given by
g2
22
0
r
zz
(1)
(a) (b)
Fig. 3.16 Oil feeding reservoir
0
z is the datum level, is the angular velocity of the rotation and
r
is
the radius. Setting 0
0
z , a portion of the free surface is a paraboloid of
revolution. Denote
1
z and
2
z as points on the lower wall and the upper
:
:
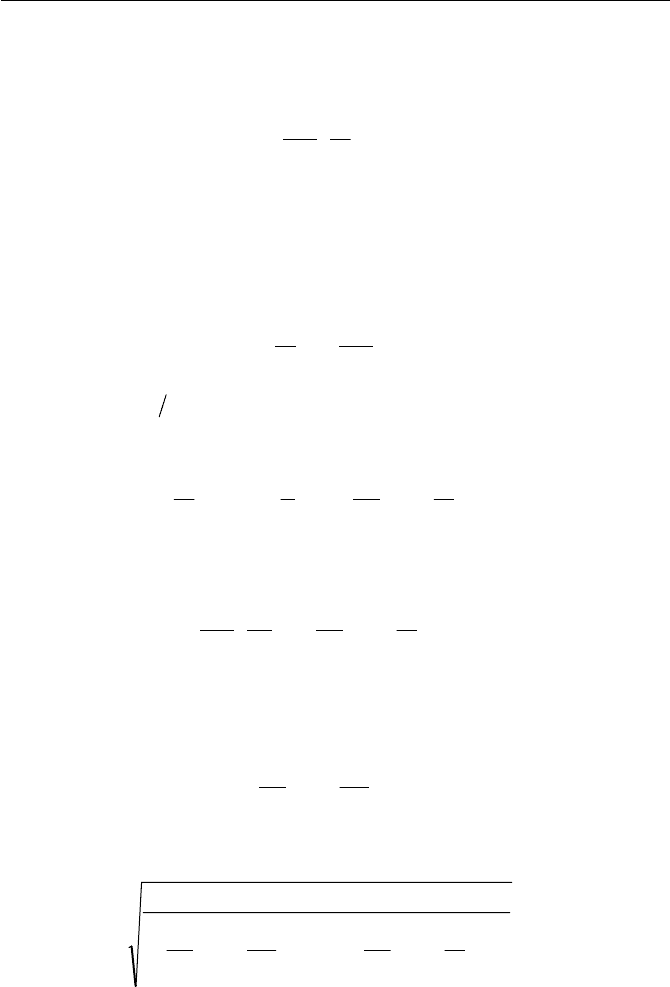
Exercise 109
wall of the container respectively from the level 0
0
z . From Eq. (1),
1
z
and
2
z are thus given by the following formula
2
2
2
22
¸
¹
·
¨
©
§
D
z
g
(2)
bzz
21
(3)
From Eqs. (2) and (3), the radius of the free surface
1
R at the level of
1
z is
easily obtained from
b
D
R
2
2
2
1
2
2
g
¸
¹
·
¨
©
§
(4)
Knowing radii
2D and
1
R , we can obtain the volume of oil V contained
after rotation from
b
DDb
R
D
V
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
22
12
1
2
2222
SS
(5)
This is further written in terms of the known parameters as
»
»
¼
º
«
«
¬
ª
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
b
DDb
V
22
1
2
2
222
2
S
g
(6)
The oil volume contained at the original state before the rotation, is given
by
h
DD
V
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
2
2
2
1
22
S
(7)
From equating Eqs. (6) and (7), we can obtain the required as
b
DD
h
DD
b
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
22
1
2
2
2
1
2
2222
g
(8)
To find the pressure at point A as indicated in Fig. 3.16, we use Eq.
(3.1.40)
:
:
:
:
:

110 3 Fluid Static and Interfaces
aA
pzR
D
p
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
1
2
1
2
1
2
22
1
g
UU
(9)
Also, by Eqs. (1), (2), (3) and (4), we can calculate
A
p as
a
A
pb
b
DD
h
DD
b
DD
p
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¹
·
¨
©
§
g
g
U
U
2
2222
2
2
22
1
22
1
2
2
2
1
2
22
1
(10)
This is an example of an oil feeding reservoir for lubricating and cool-
ing a vertical shaft bearing. Installing an oil feed tube at point A, oil is fed
to the bearing part with pressure
A
p when the shaft is rotated with angular
velocity .
Problems
3-1. Obtain the pressure if a
U
-tube manometer, which is installed at the
pipe centerline, of a horizontal oil transportation pipe and reads
200 mmHg. The oil in the manometer is depressed 150 mm below the
pipe centerline. The density
0
U
of the oil is
33
mkg10800 u. and the
density
m
U
of the mercury is
33
mkg10613 u. .
Ans.
>
@
gaugemN1025.5
23
u
3-2. Calculate the atmospheric pressure, temperature, and density at an al-
titude of 15 km, in such a case as the troposphere being 11 km high.
The pressure and temperature at sea level are 101.3 kN/m
2
and
C15q respectively. The polytrophic index 1.235 n is equal in the
troposphere and it is assumed that the stratosphere is isothermal. Note
that the stratosphere is the second layer of atmosphere after the tropo-
sphere, and is extended over 11km above.
:
:
