Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

122 4 Perfect Flow

The function



P is called the pressure function. On the right side of Eq.

(4.1.23), the integral of

Ȧuu along l will become null, if we take the path

l either along a stream line or a vortex line. This occurs because u and Ȧ

are mutually perpendicular and there are no components of either vector

along the path

l . Therefore, if the flow is steady, i.e. 0 ww tu , the inte-

gral Eq. (4.1.23) yields the following formula, where the integral is carried

out either along a stream line or a vortex line to give

211

  PuPu

(4.1.26)

This is the basic form of the Bernoulli equation. The first term (in both

sides of Eq. (4.1.26) shows the kinetic energy per unit mass, the second

term is the pressure potential per unit mass, and the third term represents

the external force (body force) due to potential energy per unit mass.

Namely, the Bernoulli equation contains three kinds of energy, and total of

which are conserved. The Bernoulli equation is valid for either along a

stream line or a vortex line with inviscid, isentropic and steady flows.

When we take a surface with constant value of either a stream line or a

vortex line, Eq. (4.1.26) can be reduced to the form

const

 Pu .

(4.1.27)

This surface is often called the Bernoulli’s surface, if we choose the Ber-

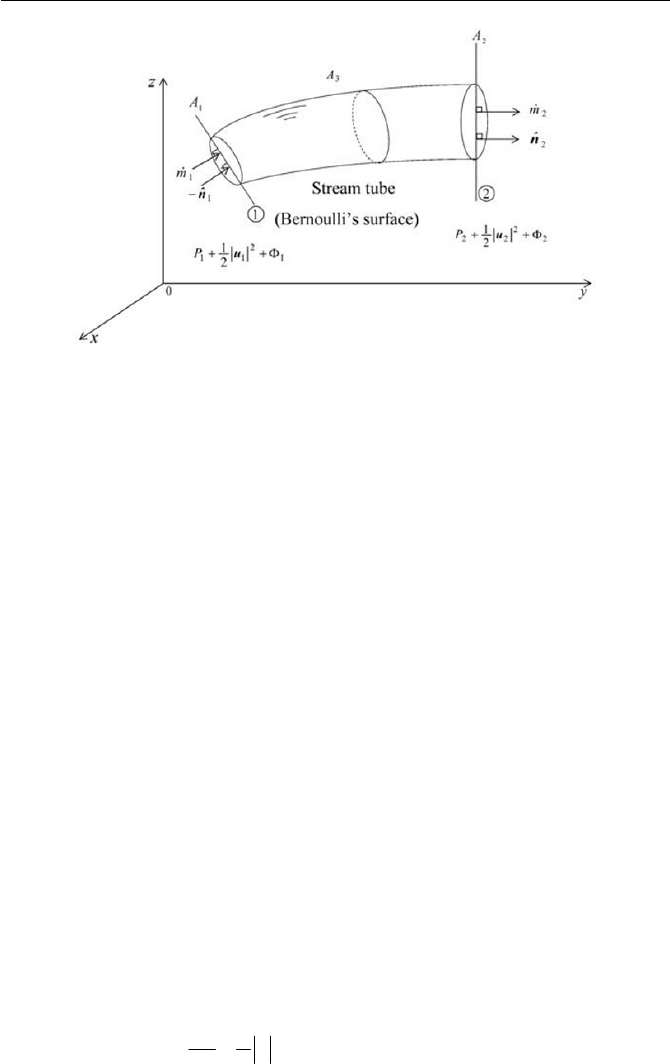
noulli’s surface as a stream tube, as depicted in Fig. 4.4. We can include

the mass continuity with the Bernoulli equation. Often such one dimen-

sional flow equations are used in many engineering problems. From the

continuity equation of Eq. (2.1.5), assuming a steady flow, a volume inte-

gral to an element of the stream tube,

–٤

in Fig. 4.4, gives

0 

(4.1.28)

Moreover, by the Gauss’s divergence theorem, it becomes

0 

Su d

(4.1.29)

Additionally, over the entire surface of the stream tube we have

321



³³³

SuSuSu ddd

AAA

UUU

(4.1.30)

Since there is no flow across the surface of the stream tube of the Ber-

noulli’s surface, the third term of Eq. (4.1.30) is zero.

))

)

4.1 Potential and Inviscid Flows 123

Fig. 4.4 Bernoulli’s theorem

SuSu dd

 

³³

(4.1.31)

If we take an outward surface positive and at ٤

and ٤

namely at the inlet

and outlet respectively,

Sn dA and

๸ Sn d are assumed, we resul-

tantly derive the mass continuity as follows

222111

Au=ȡAuȡ

(4.1.32)

and

const. uAm



(4.1.33)



is the mass flow rate, which is conserved at any position along the

stream tube, see also Exercise 2.1. The set of equations, Eqs. (4.1.27) and

(4.1.33), are often used to solve engineering problems, that is, the Ber-

noulli equation together with the mass continuity may be used or reduced

to appropriate forms under various flow situations.

If a flow is irrotational, the velocity field has a scalar potential, similar

to Eq. (4.1.2) as

ේ u

(4.1.34)

Furthermore, if we assume a time dependent inviscid flow, we can obtain a

more general form of the Bernoulli equation from Eq. (4.1.23) in the same

manner



tfP



(4.1.35)

)

124 4 Perfect Flow

Equation (4.1.35) is often called the pressure equation and has more broad

application in time dependent inviscid flows (for perfect flow).

In many engineering applications of hydraulics, flows are to be steady

incompressible and the body force (external force) is gravitational, so that

and can be written as

and zg

(4.1.36)

g is the gravitational acceleration, and z is the coordinate from a datum

level in the gravity field. So Eq. (4.1.35) can be written together with the

continuity equation as follows

const.

uAQ

(4.1.37)

and

const.

 zpu g

(4.1.38)

Q is the volume flow rate. In hydraulics, Eq. (4.1.38) is often called the

Bernoulli equation (energy per unit volume). We may also express Eq.

(4.1.38) in another form

 const.

(4.1.39)

The Bernoulli equation of (4.1.39) is a form with a unit called head [m],

and it states that the sum total of velocity head, pressure head and potential

head remains constant along a stream tube (Fig. 4.4) for steady, incom-

pressible and inviscid flow. The sum total of these three types of head is

also called the total head

[m].

The Bernoulli equation can be further extended in the rotating refer-

ence frame, such as often encountered in turbo machineries. The accelera-

tion of a fluid particle, which implies the stream tube between

and ٤

relative to the inertial reference frame, is derived in Eq. (1.2.12). Using the

first integral of the Euler equation in the rotating reference frame, the for-

mula may be written

³³ ³³

³³ ³

uu 









lulȦul

lul

ddddp

drdd

rrr

(4.1.40)

)

4.1 Potential and Inviscid Flows 125

In hydraulic turbo machineries, the gravitational body force (the poten-

tial head) and the Coriolis force can be ignored compared to other domi-

nant forces, so that the integral Eq. (4.1.40) along a stream line yields the

following form, assuming the flow is steady and incompressible

const.



ggg

uwp

(4.1.41)

w is the relative velocity in a rotating reference frame and u is the rotat-

ing speed of the stream tube to the inertial reference frame, i.e.

(4.1.42)

Through Eqs. (4.1.40–4.1.42)

is the radius of the stream tube from the

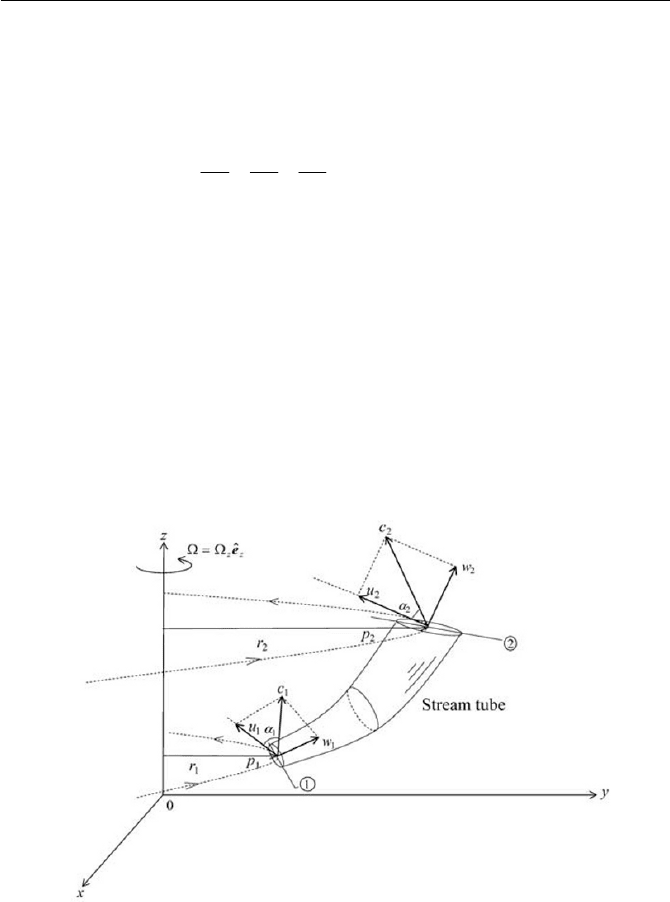
axis of rotation. A detailed schematic is displayed in Fig. 4.5. It is men-

tioned here that it is sometimes convenient (or rather conventional) to draw

a diagram to obtain the absolute velocity c at both end

or ٤

in design-

ing turbo machineries. The vector sum of these velocity diagrams, as

shown in Fig. 4.5, is called the velocity diagram, which is explained in

more detail in later chapters.

Fig. 4.5 Kinematic configuration of rotating stream tube

In engineering applications of fluid mechanics, one is often interested

in estimating the overall force acting on a device in a region of space,

where fluid enters and leaves. By extending a volume element, with which

basic governing equations of fluid motion were derived in the previous

chapter, we can identify the region of interest in fluid flow as a control

126 4 Perfect Flow

volume. A control volume may be fixed in space, or be moved with defor-

mation in a turbo machinery, and it is recognized that the basic laws of dy-

namics can be applied directly to the control volume. The same holds true

for the fluid particle concept. The conservation of linear momentum of the

fluid particle given by Eq. (2.2.1), thus, directly applies to a control vol-

ume as follows

(4.1.43)

f represents the various forces acting on the control volume. Equation

(4.1.43) is a form of Newton’s second law of motion. In classical dynamics,

Newton’s second law is always the starting point. The inertia term of Eq.

(4.1.43) can be written in an integral form over the control volume, which

is fixed in space, according to Eq. (2.2.4)





dSdV

fnuuu

(4.1.44)

The second term on the left side of Eq. (4.1.42) is the net momentum flux

across the control surface, and



dSnu

 is simply the volume flux for each

surface element

dSn

Equation (4.1.44) can be applied to a control volume, of a portion of

stream tube or equivalently a device which has an entrance and an exit

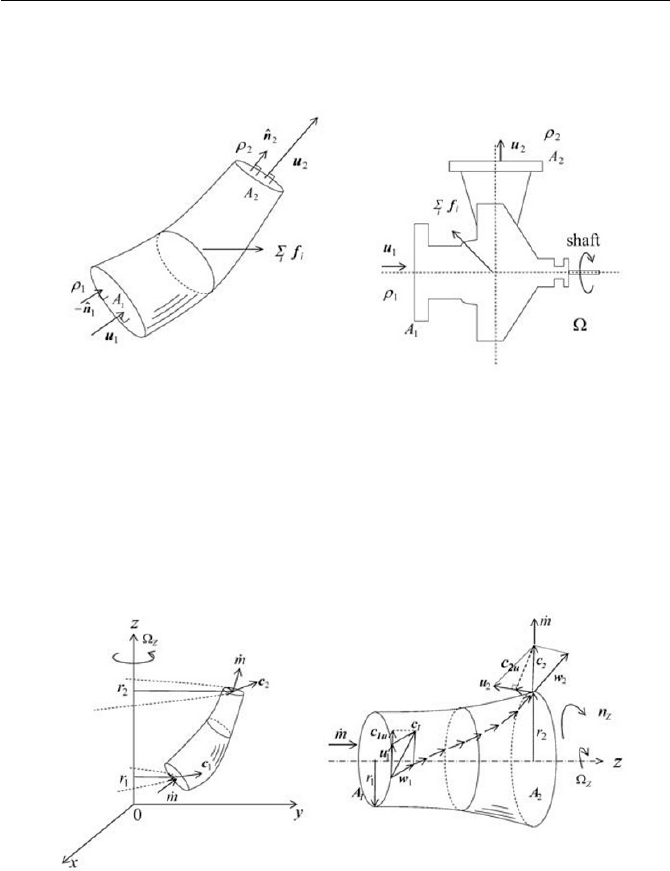
across which the flow may be uniform, as depicted in Fig. 4.6. Note that

Fig. 4.6(a) is a stream tube when the forces

f are applied, and Fig

4.6(b) is a more specific example of a configuration of single-suction

pump treated as one control volume. The flow is rotated in the pump by

axial shaft rotation of and the flow velocity at the outlet

u is 90º di-

verted from inlet

u to discharge at higher pressure. Assuming the flow is

steady, Eq. (4.1.44) can be considerably simplified as

 

dSdS fnuunuu

6 

³³

ˆˆ

22111

(4.1.45)

and

 

AuAu fuu



22221111

(4.1.46)

At the entrance,

u nu

, since the surface element dSn

faces inward

and at the exit,

u  nu

. Thus, with the mass continuity by Eqs. (4.1.33),

(4.1.46) can be written

4.1 Potential and Inviscid Flows 127

(a) Stream tube (b) Single-suction pump

Fig. 4.6

Forces on control volume

(a) Rotating stream tube (b) Generalized turbomachine

Fig. 4.7 Moment of momentum on control volume

128 4 Perfect Flow



m fuu





(4.1.47)

Note that Eq. (4.1.47) is a vector equation, with which Bernoulli equation

of Eq. (4.1.26) and the mass continuity equation of Eq. (4.1.32) are valid.

Forces

f , acting upon a control volume, can be a gravitational force

(body force), a pressure (surface force), etc, and the sum of which is the

net force that alters the flow directions

u and

u resultantly.

Knowing the linear momentum equation given by Eq. (4.1.47) of a

control volume, we may be able to derive a moment-of-momentum equa-

tion for a control volume directly from the conservation of angular mo-

mentum for a non-polar fluid, i.e. the pseudovector A is identically zero.

Similar to Eq. (4.1.43), the linear momentum equation, we can write a

moment-of-momentum equation (to be more exact, the angular momentum

of linear momentum equation), according to Eq. (2.3.1)



nux

(4.1.48)

n represents the torques (due to various forces) acting on a control vol-

ume. We can apply the Reynolds’ transport theorem of Eq. (1.5.10–4.1.48)

so that we can write



³³

u

dSdV

nnuux

(4.1.49)

In the same manner that we derived the linear momentum equation of Eq.

(4.1.47), assuming the flow is steady, Eq. (4.1.49) is written in a consid-

erably simple form for a portion of stream tube, as shown Fig. 4.7(a) rotat-

ing around an axis of

z with an angular velocity

, as follows



uu

m ncrcr

1122



(4.1.50)

r and

r are position vectors of inlet and exit of the rotating stream tube

respectively, and

c and

c are corresponding absolute velocities at inlet

and exit respectively. Equation (4.1.50) is the moment-of-momentum

equation for a control volume. It can be applied to the control volume en-

closing the rotor of a generalized turbomachine, with reference to Fig.

4.7(b), as follows



zuu

ncrcrm



1122



(4.1.51)

Exercise 129

and

are the circumferential absolute velocities of entering and

leaving flow from the rotating control volume (turbomachine) respectively

and

n is the net torque, acting on the control volume. Note that

u and

are the circumferential velocity of rotating control volume in Fig. 4.7(b),

where in the diagram the direction of

u is rather toward the paper surface,

but is deliberately oriented in a different direction for the sake of clarity.

Equation (4.1.49) is directly obtained from Eq. (4.1.48), because we know

that

cr A and

cr A are the inlet and outlet conditions. In Fig. 4.7(b),

it is further noted that

w and

w are relative velocities,

u and

u are

circumferential velocities (often referred to as the blade speed) respec-

tively at inlet and exit of the rotating control volume (turbomachine). The

rate of energy

P , at which the control volume (turbomachine) does work

on the fluid, is expressed by

zzw

nP 

(4.1.52)

and



uuw

cucumP

1122





(4.1.53)

The Eq. (4.1.53) is sometimes referred to as Euler’s pump or turbine equa-

tion as well, depending on

P or 0

P respectively. See also Exer-

cise 2.3.

Exercise

Exercise 4.1.1 Measurement of Flow Velocity by a Pitot Tube with

Mach Correction

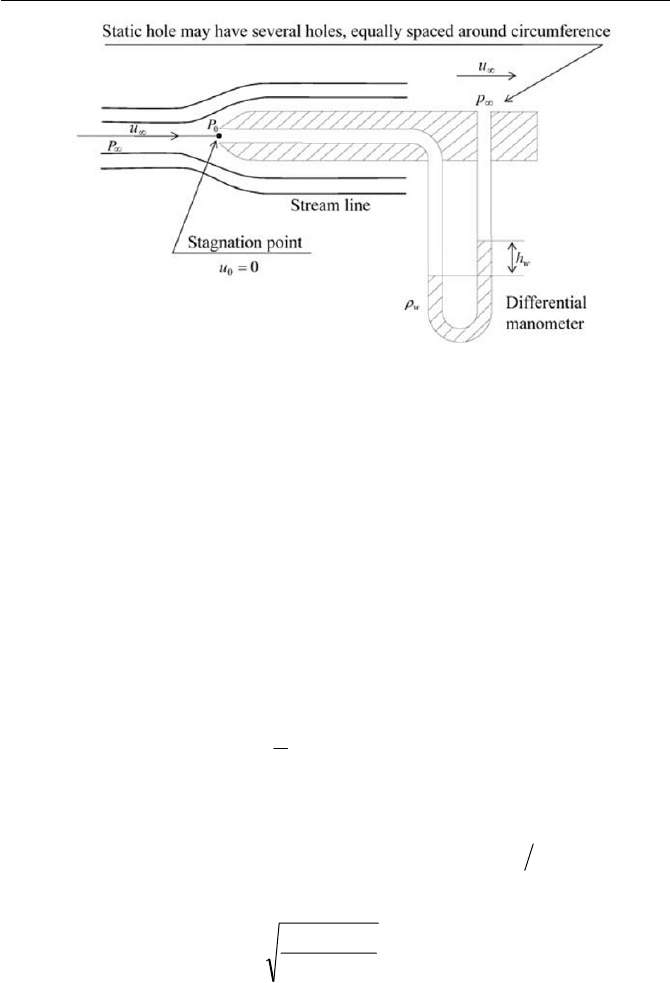
A velocity-measuring instrument called a Pitot tube, as show in Fig. 4.8,

named after its inventor, Henri de Pitot (1695–1771), consists of the stag-

nation hole at the front of the tube measuring

p while the static holes on

the side sense

. The velocity can be measured, knowing the pressure

difference (

 pp

), by a differential such as U-tube manometer, as de-

picted in Fig. 4.8. Explain the measurement principle, and discuss if the

flow is not incompressible.

130 4 Perfect Flow

Fig. 4.8 Pitot tube

Ans.

Consider the Bernoulli equation of Eq. (4.1.38), which holds true at

any point along the stream line of the flow. At the front of the tube (in fact

any body immersed in a free stream), there is a stagnation point, at which

the flow is diverted down stream and the velocity is zero. On the other

hand in the upstream and downstream of the free stream, particularly close

to a static hole (more strictly at a point along the stream line diverted from

the stagnation point), the static pressure is

p with the velocity of

u .

Thus, the Bernoulli equation will be

 pup

(1)

The gravitational potential (pressure head) is ignored due to small potential

difference between the stagnation hole and the static hole. It is noted that

p is sometimes called the stagnation pressure and 2

is called the

dynamic pressure. From Eq. (1),

can be obtained by





(2)

A differential manometer placed across the output of these values reg-

isters the pressure difference



 ppp

, which is measured such that

Exercise 131

(3)

is the density of the liquid column and

h is the reading for the col-

umn difference. Therefore, knowing

, the density of the fluid in priori,

we can obtain the fluid velocity

u by Eq. (2), measuring p by a differ-

ential manometer. In order to obtain accurate measurement, the position of

the static holes is recommended as

d6 apart from the stagnation hole,

where

is the diameter of the tube and 2d is the diameter of the stagna-

tion hole.

A substantial error may occur if the tube is yawed with an angle facing

the flow direction. Care must be taken in determining whether the direc-

tion of

u is parallel to the axis of the tube, checking that p reading al-

ways remains at maximum with respect to the flow direction. Also when

the velocity of a compressible flow becomes higher, a correction of com-

pressibility becomes necessary. Although further details of the compressi-

ble flow analysis are given in the later chapter, we will consider here the

correction of compressibility, commonly called the Mach correction of the

Pitot tube.

This is done by considering the energy equation of the compressible

flow with reference to Eq. (5.2.9), so we have







(4)

Equation (4) is the one dimensional steady compressible energy equation

(ignoring gravitational potential), which is equivalent to Eq. (1), and where

k is the specific heat ratio of the flow defined by

cck / . From Eq. (4)

with the definition of the Mach number

, i.e. auM /

෱

, where a is the

sound speed, Eq. (4) can be rewritten as follows, with reference to Eq.

(5.2.15)





(5)

The right hand side of Eq. (5) can be expanded with binomial expansion









422

(6)