Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

152 4 Perfect Flow



pRp



(17)

Note that

p is the vapor pressure of the bubble at a given temperature and

is the surface tension of a vapor-liquid interface.

Exercise 4.1.6 Kelvin’s Circulation Theorem and Lift on Airfoil

For a steady barotropic flow of a perfect fluid, show that the circulation

around any closed material curve is invariant. Explain how the lift of an

airfoil is generated when the potential flow starts up around the airfoil.

Note that the motion of the fluid is called barotropic if the density and

pressure are directly related. The simple relation between

and

is such

that



 

where

is the pressure function. The fluid itself is called piezotropic

when the pressure and density are directly related. Thus all piezotropic

fluid flows are baratropical.

Ans.

The Euler Eq. (4.2) can be written in terms of the pressure function

(4.1.25) and a body force potential (gravitational potential function)

(4.1.22) as follows

g p



 P

(1)

where

 g

(2)

and



(3)

The left hand side of Eq. (1) is the material derivative and the acceleration

of the flow is expressed by

)

Exercise 153

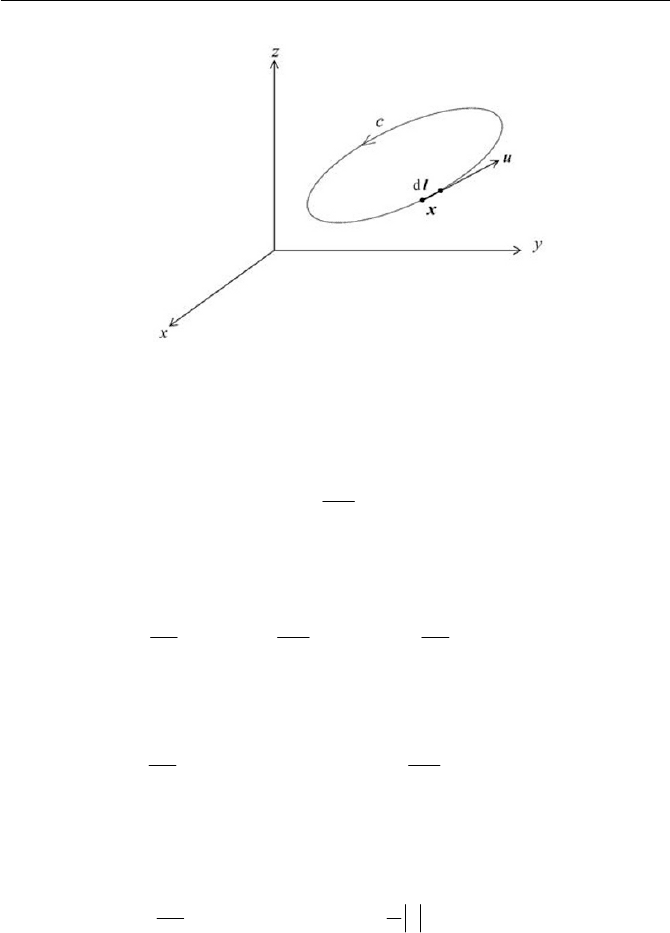
Fig. 4.16

Circulation around

(4)

Let us consider the circulation around any material closed curve

c and ex-

amine the time derivative of the circulation as follows

³³³

 

ccc

(5)

Denote the coordinate of a point on

c be

and the line element xl dd ,

which moves with flow, so that Eq. (5) becomes

³³

³³³



 

ccc

ddd

uuxa

uxalu

(6)

Thus

³³³

 

ccc

ddd

uxalu

(7)

The second integral of Eq. (7) vanishes identically due to the cyclic inte-

gral of the total differentiation being zero. For the barotropic flow, the first

integral also vanishes. This is because from Eqs. (1) and (4), that is

154 4 Perfect Flow





 

³³

xxa

(8)

Therefore



(9)

It follows that the circulation is kept constant, i.e.

const.

(10)

This is Kelvin’s circulation theorem, Kelvin (1869). It states that, for

steady barotropic flow, in a continuous motion of the perfect fluid under

the conservation force, the circulation around any material closed curve,

that is moving with the flow, is kept constant. It is mentioned that there are

conditions, in which the motion of a viscous fluid at a very large Reynolds

number may be approximated to that of a perfect fluid. It is useful to con-

sider the inviscid limit in many engineering problems such an airfoil, as

mentioned in the proceeding problems.

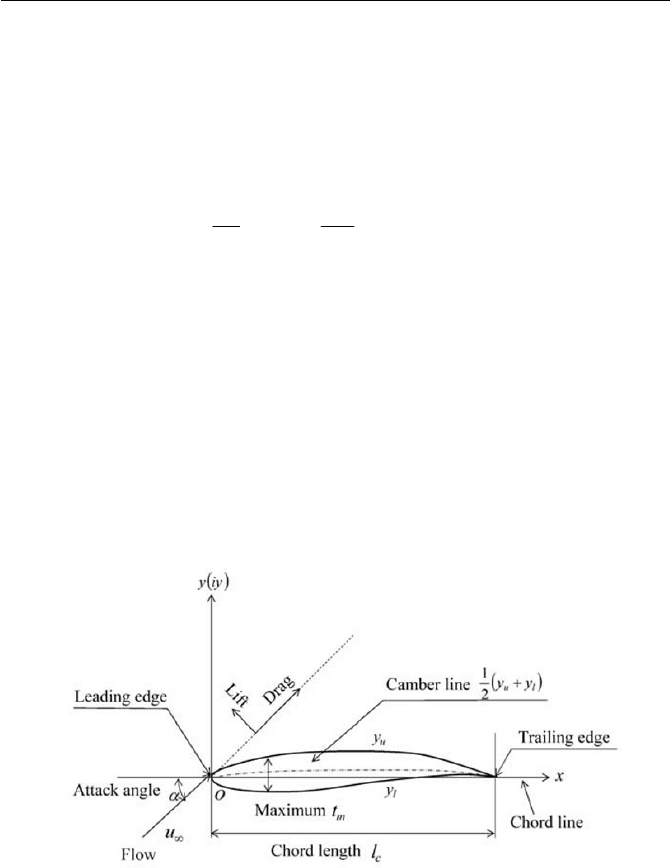
Fig. 4.17 Airfoil nomenclature

Figure 4.17 shows a schematic of an airfoil (aerofoil) and its nomen-

clatures in common use. Note that the schematic of the airfoil in Fig. 4.17

is drawn thick and exaggerated for the sake of clarity. The camber line is

the mean profile. The shape of an airfoil is designed in many ways to meet

engineering demands, but they are usually well rounded at the leading

)

Exercise 155

edge and sharp at the trailing edge. When the ratio of the maximum thick-

ness to the chord length



and the ratio of the maximum camber to

the chord length are small, we consider the airfoil is thin.

The lift force and drag force are exerted by an airfoil, and they are

normal to each other in the direction of flow as shown in Fig. 4.17. The

angle

between the approaching free stream and the chord line is called

the attack angle. The attack angle is usually supposed to be small.

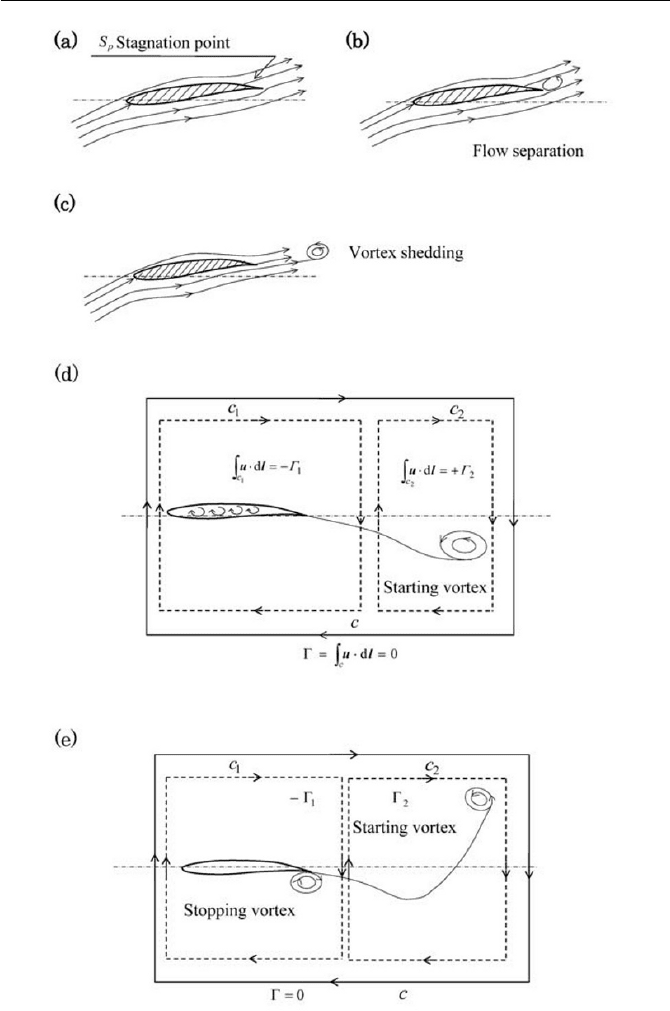
Now for the question of the lift as the flow starts up, we consider the

potential flow of a perfect fluid with no circulation immediately after the

startup. The stagnation point

is observed on the airfoil in the vicinity of

the trailing edge as shown in Fig. 4.18(a). This phenomenon will be treated

in the next problem in detail; at this moment the velocity and the pressure

are infinite at the trailing edge, where the sharp bend flow persists around

the trailing edge. In real situations, soon after the start-up, the stagnation

point

moves to the trailing edge, and at the same time a small vortex,

due to the flow separation, is formed and after a few moments it is shed

and lost downstream. The vortex generated after the startup is called the

starting vortex as depicted in Fig. 4.18(b) and (c).

In order to discuss the lift on an airfoil, we must look at the circulation

around the airfoil. The airfoil circulation has recently been studied in more

detail and is considered to be an important factor. However before pro-

ceeding further, it is interesting to develop a deeper insight into how the

circulation is generated phenomenologically. Figure 4.18(d) is a schematic

expressing how circulation around an airfoil is generated when the flow is

starting up. By Kelvin’s circulation theorem the total circulation

in a

flow domain bounded by a closed curve

c must be constant and kept at

zero, since the flow is in a quiescent state at the beginning. After the start-

ing vortex is created, the circulation in a closed curve

c has a value,

say



z

, since inside the curve there is a starting vortex. The total

circulation in the fluid must be constant in time

, and hence

 ,

which is the circulation in a closed curve

c and must exist to cancel

is equal but of opposite sign to the starting vortex

as shown in Fig.

4.18(d). Thus, we have a relationship



 

(

11)

What is happening about the airfoil is that a group of so-called bounding

vortex is being formed around the region of the airfoil hypothetically to

produce



in the closed curve

c . It should be mentioned, not to con-

***

156 4 Perfect Flow

tradict the irrotational flow assumption, that owing to the Stokes integral

theorem

³³

u  

dd Sulu

(

12)

Thus, the distribution of vorticity Ȧu u on the airfoil surface must be

considered. The starting vortex falls far behind after some time, and the

airfoil gets lift

L due to

. The derivation of the lift on an airfoil will be

described in the proceeding paragraph. A large closed curve

c , including

the airfoil and the starting vortex, always gives zero circulation

al-

together, even as time elapses. With the same analogy, a vortex appears

when the flow is stopped, which is called a stopping vortex. The stopping

vortex is generated about the airfoil to encounter

 and is released from

the airfoil, keeping the total circulation zero, i.e. 0

 . Those

two vortices, namely the starting vortex and stopping vortex, are shed as a

pair after the flow is stopped. Isn’t it interesting? There would be vortices

all over the place in this world, if only the perfect fluid existed.

The circulation around an airfoil

 is therefore determined by shift-

ing the stagnation point

to the trailing edge. The flow leaves the airfoil

with a finite velocity at the trailing edge without bending around the edge,

where the pressure difference at the edge between upper and lower surface

of the airfoil becomes zero. The condition to determine

 around the air-

foil is justified by shifting

to the trailing edge. This is called the Kutta

condition, and the sequence of this phenomenon is also called the Kutta-

Joukowski hypothesis. The Kutta-Joukowski hypothesis simply states that

infinite velocities are not admissible in real flow situations.

The origin of the lift of a body placed in a potential flow can be de-

rived from a thought that the force





FF , F acting on the body is the

net force due to pressure on the body, which is given by



PdSF

(13)

c is the closed curve of the body surface and Sd is the surface element

on the body, i.e.

dSd nS

; n

is the unit normal vector facing outward on

the body surface. The components

F and

F are written by

³³ ³

  

00 0

cc c

PdydS

PdSPnF

(14)

and

***

Exercise 157

Fig. 4.18 Starting up flow around an airfoil

158 4 Perfect Flow

³³³

  

000

ccc

PdxdS

PdSPnF

(15)

Thus,

is expressed by the complex expression



 

dzPi

idydxPiiFF

)(F

(16)

idydxdz  is the conjugate of idydxdz  . From Eq. (1) for the steady

barotropic flow, we have (with reference to Eq. (4.1.21))



 u PȦuu

(17)

Considering the potential flow, i.e. 0



uȦ irrotational, the pressure

of Eq. (17) is substituted into Eq. (16), which gives

 

iiFF

(18)

u in Eq. (17) was expressed by the complex potential

)(zW

ivu  u

(19)

Hence

(20)

Assuming that there would not be external body force, i.e. 0 , Eq. (18)

becomes



dWi

iFF

(21)

In the potential flow, the body surface itself is the stream line, i.e. the

closed curve

c is the line of Const.

, so that

³³³

000

ccc

(22)

)

Exercise 159

Further, since



zW is the analytic function, the integration

dz~ can be

performed with an arbitrary closed curve, say

, around the body, which

is expressed as



dWi

iFF

(23)

Equation (23) is known as Blasius’ first theorem, Blasius (1910). In a simi-

lar manner, the moment

M about the origin of the normal stress exerted

on the body is

 



 

³³

zdz

zzd

ydyxdxPM

(24)

Re indicates the real part of the complex number. Equation (24) is also

known as Blasius’ second theorem, Blasius (1910).

The Blasius theorem can be applied to any steady irrotational flow in

surrounding the body. The complex function

dzdW may be expanded for

z with a sufficiently large order as

}





(25)

is the approaching free stream and

is the attack angle.

dzdW

gives the complex velocity in the z -plane with the velocity potential



being



}





zAzeUzW

(26)

The second term in Eq. (26) is the complex potential due to circulation

᧭

so that we have



}





DDD

iii

ieU

(27)

From Blasius’ first theorem we can obtain the force

acting on the body:

160 4 Perfect Flow

eUi

iiiiFF



 

(28)

Equation (28) is the Kutta-Joukowski theorem, stating that the net force on

the body is directed perpendicular to

and

 ULF

(29)

Thus, the lift L is generated due to

, which may be dependent upon the

velocity field around the airfoil. It should be mentioned that there would be

no force acting on the body (airfoil), where there would not be source

0 q (Eq. (4.1.15)) on the solid wall, for the direction parallel to

, i.e.

0 DF

(30)

This is the D’Alembert paradox, stating that there would be no drag force

acting upon a body placed in a potential flow. Drag force is produced by

surface friction in the boundary layer, which will be discussed in the pro-

ceeding chapters.

In the same manner, Blasius’ second theorem gives the moment

M by

substituting Eq. (27) into Eq. (24). See Problem 4.1-9.

Exercise 4.1.7 Joukowski Airfoil

Two dimensional airfoils are necessary for the preliminary design of air-

plane wings, propeller blades, wind turbines and so forth. In those engi-

neering airfoil applications the lift force is the prime aim for an airplane to

support its own weight against gravity or for the one blade of a rotating

propeller or wind turbine to exert the torque. A body placed in the potential

flow may not experience the drag force, but has indeed the lift force, which

is the major concern in this exercise. The simplest airfoil among many is

the Joukowski airfoil, which can be obtained from the flow around a circu-

lar cylinder by a conformal transformation known as the Joukowski trans-

formation as introduced in Eq. (4.1.19).

Examine shapes of the Joukowski airfoil and give the lift and moment.

Ans.

From Riemann’s conformal mapping theorem, there exists an analyti-

cal function that an outside domain of an arbitrary body expressed by a

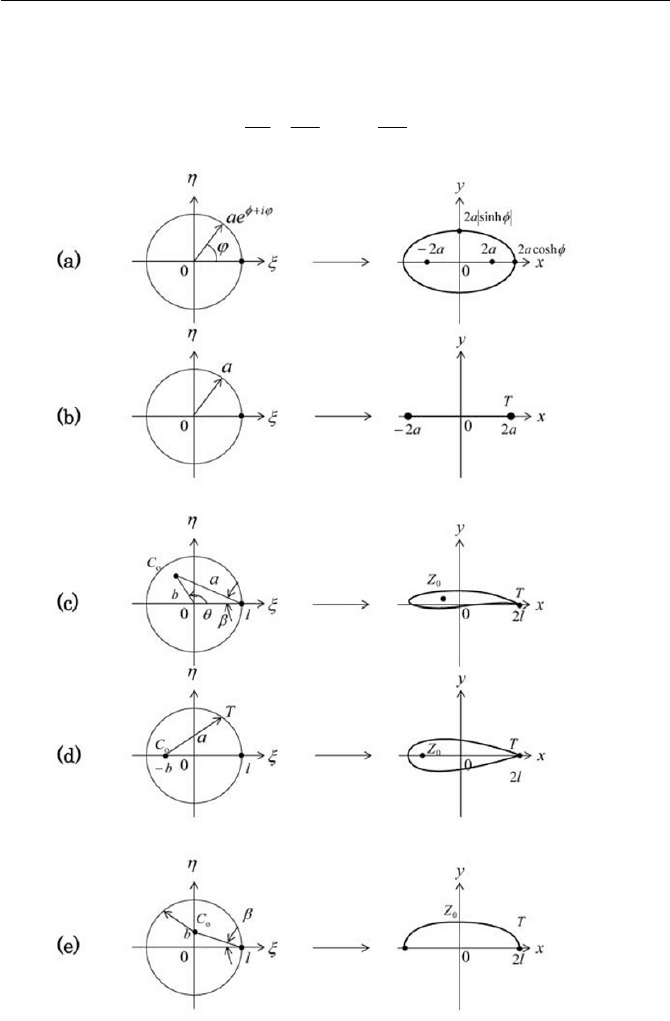
Exercise 161

closed surface in the

]

-plane can be conformally transformed to the

plane as the outside domain of a circle. The transformation from

]



]]

]

(1)

Fig. 4.19 Joukowski transformation