Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.


162 4 Perfect Flow
Equation (1) is the Laurent polynomial expansion, where complex con-
stants
n
CCCC
210
,,
are chosen to give an appropriate airfoil shape.
The Joukowski transformation is such that
]
]
2
a
z
(2)
yxiyx ,,
[
K
]
, iy
x
z and
a
is a positive real constant. Equation
(2) gives the Joukowski airfoil shape, depending upon the choice of the cir-
cle in the
]
-plane. Figure 4.19(a)–(e) are various cases of airfoil shapes.
Let us denote a circle in the
]
-plane as
I
aeR
. The singularity of the
transformation is a point, which is obtained from the relationship
01
2
2
z
a
dz
d
]
(3)
This gives us a
z
r . In an airfoil, az is chosen at the trailing edge.
Now let us set a circle in the
]
-plane by writing
]
as
MI
]
i
ae
(4)
I
and
M
are real constants. The transformation of Eq. (2) thus provides us
with
^
`
)(
MIMI
ii
eeaz
(5)
And in the
z
-plane after eliminating
M
, Eq. (5) affords us
1
sinh2cosh2
2
2
2
2
)()(
II
a
y
a
x
(6)
For constant
I
, Eq. (6) supplies an equation of an ellipse with semi-major
axis ,cosh2
I
a semi-minor axis
I
sinh2a and foci ,2ax r ,0 y as
shown in Fig. 4.19(a). Therefore, R=
Constant
I
]
ae ; a circle with the
center at the origin of the
]
-plane, will be transformed as an ellipse in the
z
-plane. Setting 0
I
, the ellipse is degenerated into a segment of line on
x
axis, whose length is a4 , as shown in Fig. 4.19(b). Shifting the center
of circle in the
]
-plane to a point
o
C will give
MI
]
i
o
aeC
(7)

Exercise 163
Particularly in order to set the singularity at the trailing edge, we may be
able to choose
o
C
as
TTS
ii
o
bebeC
)(
(8)
Further, we can set for
a as
2
1
22
cos2 )(
T
lbbla
(9)
When Eq. (7) is transformed to the z -plane by the Joukowski transforma-
tion of Eq. (2), the shape that appears in the z -plane is called the Jou-
kowski airfoil, as shown in Fig. 4.19(c). Particularly if
o
C is placed on the
real axis, such that
bC
o
in the
]
-plane, it becomes a symmetric Jou-
kowski airfoil. Furthermore, when
o
C is placed on the imaginary axis,
such that biC
o
in the
]
-plane, the airfoil shape may become a circular
arc airfoil. The Joukowski airfoils in (c)–(e) are to be obtained by implicit
function as follows:
(c)
z
a
z
2
]
(10)
(d)
n
az
az
na
na
¸
¹
·
¨
©
§
]
]
(11)
(e)
3
3
2
21
0
z
C
z
C
z
C
zC
]
(12)
The most typically used airfoil type in engineering application is found
in (c), which also gives the general flow configuration of a uniform stream
over a cylinder. As seen in Fig. 4.19(c), the Joukowski airfoil has a cusp at
the trailing edge so that there would be strength problems in actual usage.
Since the Joukowski transformation, Eq. (2) can be equivalently rewritten
by the following expression:
2
2
2
¸
¸
¹
·
¨
¨
©
§
a
a
az
az
]
]
(13)
The power of 2 in Eq. (13) can be replaced by the integer n, expanding the
general form, which gives the following expression:

164 4 Perfect Flow
n
a
a
naz
naz
¸
¸
¹
·
¨
¨
©
§
]
]
(14)
Equation (14) is called the Kàrmàn-Trefftz transformation and the airfoil
generated by the transformation from the cylinder (a circle in the
]
-plane)
is referred to as the Kàrmàn-Trefftz airfoils, see Fig.4.20(a). More general
transformation can be derived directly from Eq. (1), taking the terms up to
n, i.e.
n
n
CCC
Cz
]]]
]
2
21
0
(15)
The airfoil design based on Eq. (15) is referred to as the Mises airfoil,
see Fig.4.20(b). These airfoils, based on the transformation by Eqs. (14)
and (15), are flexible in design because of choices of the singularity points
that are located in the appropriate positions, so that optimum design of an
airfoil will be possible and be able to meet various engineering demands.
Fig. 4.20 Other airfoil shapes
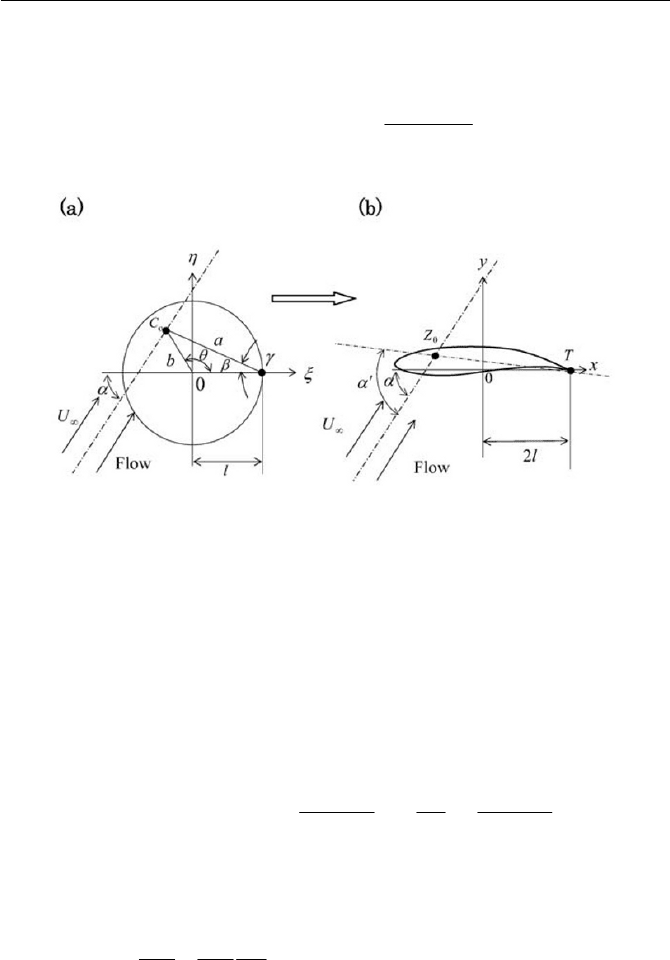
Referring to Fig. 4.19(c), the cylinder (a circle in
]
-plane) is mapped
into the z -plane by the Joukowski airfoil; at the same time, a flow around
the cylinder in
]
-plane can also be mapped into the flow in the z -plane
by the Joukowski transformation. This expresses flow around the Jou-
kowski airfoil. In order to verify the flow field through rigorous efforts, we
can write the complex potential
]
W
in the following manner.
The flow field described by
]
W about the cylinder, whose center is
placed at
o
C , with the approaching free stream velocity
f
U at an attack
Exercise 165
angle
D
, as shown in Fig. 4.21(a). This is identically taken from Fig.
4.19(c), and can be expressed by the expression:
»
¼
º
«
¬
ª
f
T
D
DT
]
]]
i
i
ii
be
ea
ebeUW
2
)(
(
16)
Fig. 4.21 Lift and moment on Joukowski airfoil
The point where l
]
transforms into lz 2 is at the trailing edge of
the airfoil. However,
]
W in Eq. (16) has infinite velocity at the trailing
edge; as a result, the singularity at the trailing edge must be removed from
the Kutta-Joukowski hypothesis (Kutta condition) by adding a circulation.
This is done by introducing the potential vortex given by Eq. (4.1.16) into
Eq. (16), so that the singularity is removed at the trailing edge and the ve-
locity at the trailing edge can become finite. The new complex potential
W will be
¸
¸
¹
·
¨
¨
©
§
¿
¾
½
¯
®
f
a
be
i
be
ea
beeUW
i
i
i
ii
T
T
D
TD
]
S
*
]
]]
ln
2
2
(17)
With
]
W
in Eq. (17), the velocity at the trailing edge of the airfoil is
given by
dz
d
d
dW
dz
dW
]
]
for l
]
and l2
]
(18)
and

166 4 Perfect Flow
01
2
2
]
]
l
d
dz
(19)
Therefore, for
dzdW to be finite at the trailing edge,
]
ddW must be
zero, and this condition (Kutta Condition) determines the value of .
From Eq. (17), we have
0
1
2
2
2
»
¼
º
«
¬
ª
T
T
D
D
]S
]
]
i
i
i
i
be
i
be
ea
eU
d
dW
(20)
From the geometry of Fig. 4.21, we have
ET
]]
ii
aelbe
(21)
and for l
]
, is obtained from Eq. (20) as follows
D
E
S
f
sin4 aU
(22)
The lift of an airfoil can be given by the Kutta-Joukowski theorem with the
Blasius’ first theorem, see Eq. (29) in Exercise 4.1.6
U
UL
(23)
where the lift L is perpendicular to the approaching free stream. Therefore,
the lift is
DESU
f
sin4
2
UaL
(24)
In order to examine the performance characteristics of an airfoil, the
lift coefficient
L
C is often used, where
L
C is defined as a unit of length of
the airfoil. This in turn refers to the chord length
c
l or width of the airfoil,
such that
2
21
f
U
lL
C
c
L
U
(25)
It is now desired to estimate
L
C of Joukowski airfoil where, taking al
c
4| ,
we have
D
E
S
sin2
L
C
(26)
Small
D
D
E
c
;
D
c
is often referred to as the absolute attack angle,
which is greater than the apparent attack angle
D
, where we have
*
*
*
*
*

Exercise 167
D
S
c
|
2
L
C
(27)
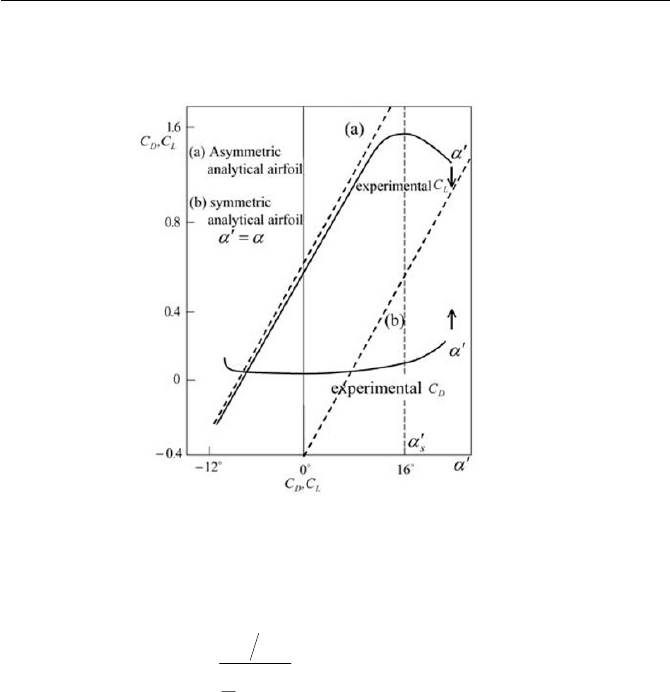
In Fig. 4.22, some comparisons with the measurement of
L
C and
D
C are
displayed, where
D
C is similarly defined by
2
21
f
U
lD
C
c
D
U
(28)
As observed in Fig. 4.22 (note that in an analytical symmetric case,
D
D
c
is also displayed with dotted line (b)),
L
C increases with
D
c
and
then drops all of sudden, where the stall of airfoil occurs at
s
D
c
. At the stall
a flow separation (the viscous boundary layer separation) from the surface
of an airfoil occurs and the circulation is lost, causing sharp drop of the lift.
However, as seen in Fig. 4.22, the analytical estimate by Eq. (27) will give
reasonable account for the (real) experimental measurement before reach-
ing the stall angle
s
D
c
. The drag of the potential flow is identically zero, as
seen in Exercise 4.1.6, except in the experiment where the viscous friction
causes the drag (due to the boundary layer), and the drag sharply increases
after the stall angle
s
D
c
caused by the flow separation.
The moment
0
M comes to the center of the origin in z -plane, whose
value is to be obtained from Blasius’ second theorem, as in Eq. (24) in Ex-
ercise 4.1.6
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
¸
¸
¹
·
¨
¨
©
§
°
¿
°
¾
½
°
¯
°
®
¸
¹
·
¨
©
§
³
³
1
1
2
2
0
Re
2
1
Re
2
1
c
c
zd
dz
d
d
dW
zdz
dz
dW
M
]
]
]
U
U
(29)
and with Eqs. (20) and (21),
0
M is expressed by
^`
DGUDJSU
ff
cos2sin2
2
2
0
bUlUM
(30)
where
J
and
G
are defined as
TS
i
beZC
0
o
,
T
S
G
(31)
and
J
i
ela
2
2
2
(32)
Thus, the moment
M
at the point
0
Z
in the airfoil, which implies the
*
shifted center of the cylinder
o
C in
]
-plane, is
168 4 Perfect Flow
DJSU
DG
f
2sin2
cos
22
0
lU
LlMM
(33)
Fig. 4.22
Some comparison of
L
C
and
D
C
with experiment (Experimen-
tal data replotted after Nishiyama, 1989)
The moment coefficient
M
C is similarly defined as following
DJS
U
f
2sin4
2
1
2
2
U
lM
C
c
M
(34)
where
ll
c
was taken tacitly.
Exercise 4.1.8 Forces on Deflectors
A liquid of an absolute velocity is deflected by a deflector to an angle of
D
forward and downward, as illustrated in Fig. 4.23. The surrounding pres-
sure is kept constant by the atmospheric everywhere, and the pressure in
liquid entering the deflector is the same as that in the liquid deflecting at
the deflection point. The jet is free-jet, the column of which is kept con-
stant without laterally spreading. The body force due to the gravity is small
and can be neglected. The viscous force is also small and neglected every-
where. The deflection of the jet is confined in the two dimensional plane,
as seen in Fig. 4.23.
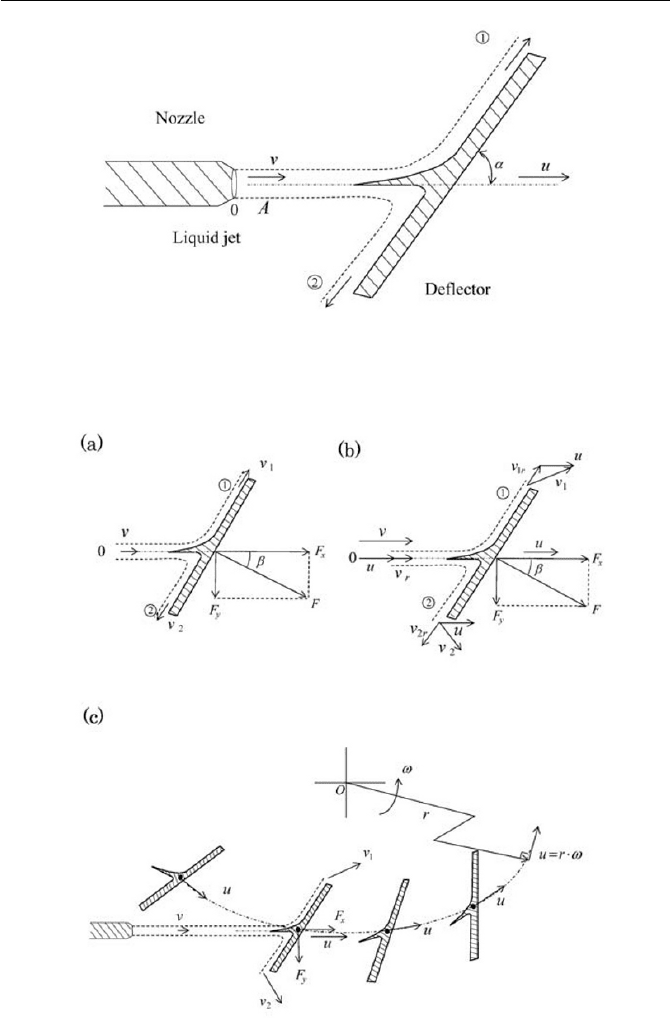
Exercise 169
Fig. 4.23 Liquid jet at deflector
Fig. 4.24 Case study of liquid jet at deflector

170 4 Perfect Flow
The area of the entering liquid jet is A , and 31 of the flow rate of the
entering liquid jet is deflected downward (to the direction
٤
2
). Examine
the following cases:
(i) Determine the force acting on the deflector and the direction of the
force when the deflector is stationary in the inertial reference frame.
(ii) Determine the force acting on the deflector, and the direction of the
force and the power of the deflector, when the deflector is moved to the di-
rection of the liquid jet with an absolute velocity u in the inertial reference
frame.
(iii) Determine the physical parameters, if a series of deflectors (a cascade)
are in action. Also describe a certain type of turbomachinery if the theory
is applied in engineering practice, and estimate the kinetic energy given to
run the machinery.
Note that the density of the liquid is
U
, which it is kept constant
throughout the process.
Ans.
The exercise is the application of the integral form of the momentum
equation over the control volume, which appears to preclude an integral
part of analysis for turbomachines, such as turbines, pumps, compressors,
and so forth.
(i) Let us consider the control volume on the deflector as illustrated in Fig.
4.24(a), defining the exiting velocities
1
v and
2
v from upward ٤
1
and
downward
٤
2
flow respectively. Denote that the forces acting on the con-
trol volume are
x
f and
y
f in
x
direction and y direction respectively,
where the entering direction of the liquid jet is in
x
direction. From Eq.
(4.1.47), the forces are
x
fvvmvvm coscos
2211
(1)
y
fvmvm 0sin0sin
2211
(2)
where for the mass flow rate
1
m
and
2
m
, we have given conditions
᧥
᧤vAQm
3
2
3
2
1
UU
(3)
᧥
᧤vAQm
3
1
3
1
2
UU
(4)
D
D
D
D

Exercise 171
Bernoulli equation gives us a clue that the magnitude of
1
v ,
2
v and v are
all equal, because from 0 to
٤
1
and 0 to ٤
2
in the control volume, we can
write Bernoulli equations as
0
2
10
2
2
1
2
1
zpvzpv
atmatm
gg
UUUU
(5)
0
2
20
2
2
1
2
1
zpvzpv
atmatm
gg
UUUU
(6)
where
atm
p is the surrounding pressure and the gravitational effect
0
zg
U
is to be neglected. Thus, from Eqs. (1) to (4), we have
¸
¹
·
¨
©
§
1cos
3
1
2
Avf
x
U
(7)
sin
3
1
2
Avf
y
U
(8)
where
x
f and
y
f are the forces acting on the control volume (to liquid
flow). Therefore, the forces acting upon the deflection are to be considered
as the reaction forces
)( cos
3
1
1
2
AvfF
xx
U
(9)
sin
3
1
2
AvfF
yy
U
(10)
The direction of the resultant forces is thus
D
D
E
cos311
sin31
tantan
11
x
y
F
F
(11)
and its magnitude is
cos610
3
1
2
22
AvFFF
yx
U
(12)
(ii) The deflector is moved with the liquid jet with the relative velocity
r
v
as
D
D
D
D
D
