Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

Problems 111

Ans.

kg/m19330

K5216

N/m101200

3-3. A circular observation window of 0.5 m in diameter is installed in an

inclined tank wall at

q60 to the horizontal level. The water is 5 m

deep above the center of the window. Determine the resultant hydro-

static pressure force on the window and the center of pressure.

Ans.



window.theofcenterthebelowm10712

N10639

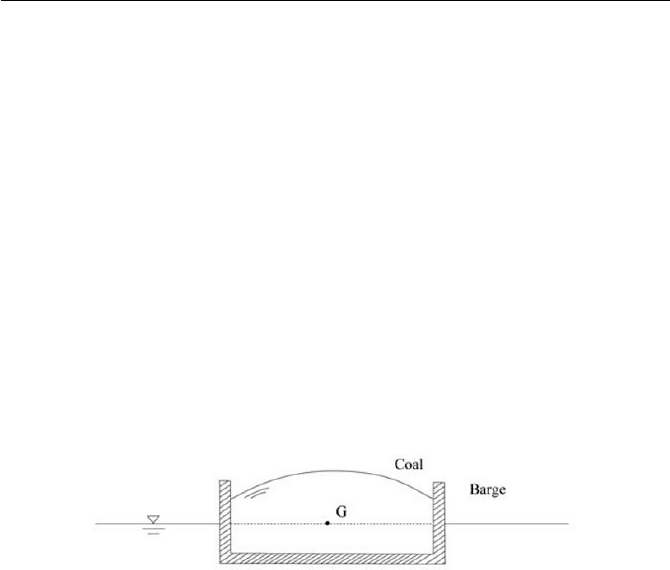
3-4. A barge is loaded with coal such that the center of gravity of the barge

with the loaded coal is at the waterline, as shown in Fig. 3.17. Discuss

the stability of the barge.

Fig. 3.17 Loaded barge

3-5. There is an air bubble 1.0×10

–3

m in diameter in the water. Knowing

the surface tension

10872



u .

N/m (water-air interface), estimate

the pressure inside of the bubble. The depth of the water where the

bubble is found is 10m below the water level. Also, calculate the di-

ameter where the bubble is raised to a depth of 5m below the water

level.

Ans.



m100991

abs.N/m109971

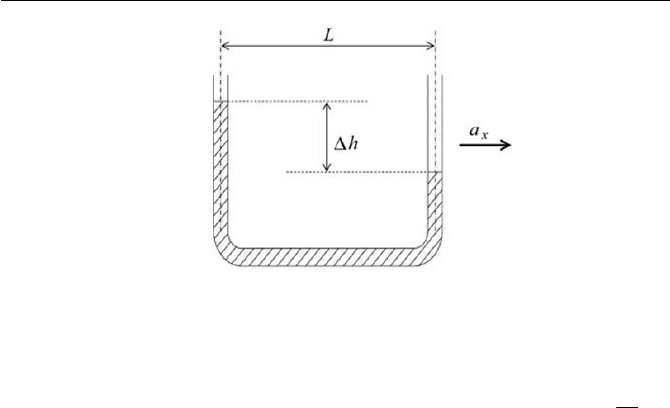
3-6. Utilizing a U-tube, an accelerometer is made to measure the accelera-

tion of a train, as shown in Fig. 3.18. The meter is mounted in the ve-

hicle so that the legs are vertical, and the tube is filled with a liquid of

. Measuring the level difference h between the legs, determine

the acceleration

a of the vehicle. The distance between the legs is L .

112 3 Fluid Static and Interfaces

Fig. 3.18 U-tube accelerometer

Ans.

Nomenclature

aA,

: area

: acceleration vector

: relative acceleration

ldba ,,,

: length (scale)

: center of pressure

dD,

: diameter

: force vector

: center of gravity

: body force

: gravity acceleration

: height or length

I second moment of surface area

product of surface

area

: unit normal vector

: thermodynamic pressure

: reference pressure

: atmospheric pressure

Bibliography 113

rR,

: specific gas constant (

) or radius

: area

: temperature

: total stress tensor

: time

: unit tangential vector

: velocity vector

: finite volume

: center of pressure (

direction)

directional centroid

: center of pressure ( y direction)

: y directional centroid

: Cartesian coordinates system

,,r

: spherical coordinates system

and

ccc

: angle

: density

: surface tension

: couple force

: scalar potential

: angular velocity

Bibliography

Basic problems in hydrostatics and fluid transport are treated to a greater ex-

tent in the following sources.

1. E.J. Shaughnessy, I.M. Katz and J.P. Schaffer, Introduction to Fluid Me-

chanics, Oxford University Press, Inc., Oxford, 2005.

2. D.N. Roy, Applied Fluid Mechanics, Ellis Horwood Limited, 1988.

3. W.P. Graebel, Engineering Fluid Mechanics, Taylor & Frarcis Publishers,

Abigdon, 2001.

4. M.C. Potter, D.C. Wiggert and M. Hondzo, Mechanics of Fluids (2nd edi-

tion), Prentice-Hall, Inc., Englewood Cliffs, NJ, 1997.

4. Perfect Flow

In this chapter, we will look at the simplest form of constitutive equations

for fluids having no viscous stress. To expand our range of applications

further, we will then extend the concept of inviscid flow to include poten-

tial flow and unidirectional incompressible flow.

Within a frame work of inviscid flow many useful formulae for turbo-

machineries will be examined in this chapter. Other examples which are

widely observed in fluid engineering are to be treated with the concept of

inviscid flow, and correspond with viscous flow at large Reynolds numbers.

A fluid with no viscous stress is often referred to as a perfect fluid, and the

constitutive equation takes the simplest form as follows

ijij



(4.1)

A detailed discussion regarding the constitutive equation of Eq. (4.1)

will be given in the following section. Presently, however, please note that

when we substitute Eq. (4.1) into Eq. (2.2.7) we can obtain





(4.2)

Here, the body force

is treated as the gravitational force (per unit vol-

ume). This equation is called the Euler equation, and is valid for inviscid

flows in general. In many engineering problems, the Euler equation is

solved or reduced into a more convenient form with the continuity equa-

tion of Eq. (2.1.5).

4.1 Potential and Inviscid Flows

When flows are far from solid surface, which is often observed outside the

boundary layer, the effects of viscosity are usually very small and it is as-

sumed that flows are frictionless and irrotational. These flows are known

as potential flows. If the flow is irrotational, the velocity field can be writ-

ten as follows, with reference to Eq. (1.1.26)

115

116 4 Perfect Flow

0 u u

(4.1.1)

Additionally, with a vector identify, it immediately follows that there ex-

ists a velocity potential

, such that the velocity u can be defined as

 u

(4.1.2)

Furthermore, if we impose the condition of a steady incompressible

flow to the potential flow, from the continuity equation Eq. (2.1.6) the ve-

locity potential

satisfies Laplace’s equation as follows



0 

(4.1.3)

and



(4.1.4)

As such

serves a harmonic function. If we further confine our consid-

eration here to two dimensional steady incompressible flows, we can in-

troduce another important scalar function, the stream function

defined in such a way that the velocity components (

vuuu ,,

) of u in

Cartesian coordinates (

yxxx ,,

{

)are given by the following relations

to satisfy the continuity equation of Eq. (2.1.6)

and



(4.1.5)

Besides which, we have the condition of irrotational flow, given by Eq.

(4.1.1) in two dimensional space written as



(4.1.6)

Substituting u and v of Eq. (4.1.5) into Eq. (4.1.6) again satisfies

Laplace’s equation, yielding the condition that

is also harmonic as fol-

lows



(4.1.7)

Note that the stream function

can be defined for any two dimen-

sional flow, or flow in two dimensional symmetric plane, regardless of

whether the flow is irrotational or not. This holds true as long as the flow

is steady incompressible.

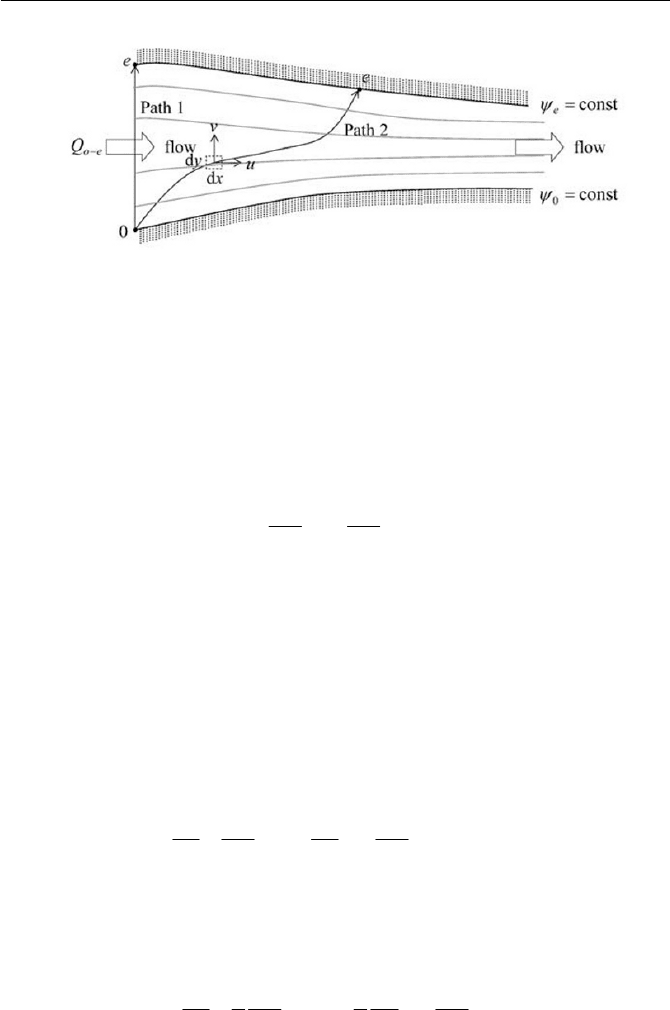
4.1 Potential and Inviscid Flows 117

Fig. 4.1 Stream function

Two important concepts arise from the stream function. First, the lines

of constant stream function

are the streamlines. Second, the difference

between the numerical values of two stream functions, such as



Fig. 4.1, is equal to the flow rate

0e

intersecting the two lines. This is

derived from following the formula



000

\\\







³³³

 e

eee

ddy

udyvdxQ

(4.1.8)

The integral Eq. (4.1.8) is independent of the path, as shown in Fig.

4.1 for path 1 and path 2. Furthermore, Eq. (4.1.8) yields the result for a

closed path

c that

(4.1.9)

Equations (4.1.4) and (4.1.7) are valid in any coordinates system, and

it has to be notified that Eqs. (4.1.2) and (4.1.5) yield the following rela-

tionships



(4.1.10)

Similarly, for instance with the polar coordinates

r and

, and the corre-

sponding velocity components

u and

u respectively, we can write the

fundamental relationships as follows

㧘



(4.1.11)

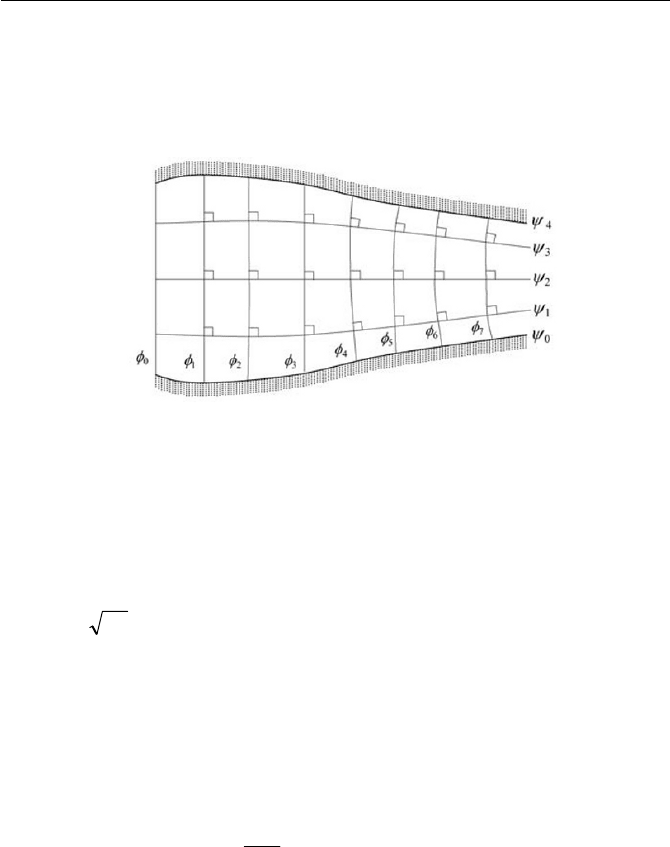
118 4 Perfect Flow

the Cauchy-Riemann conditions. An important result from the fact that

and

are harmonic, which satisfy the Cauchy-Riemann conditions, is that

lines of

and

are mutually orthogonal, as indicated in Fig. 4.2.

Fig. 4.2 Stream function

and velocity potential

Considering the fact that

and

satisfy the Cauchy-Riemann condi-

tions, a complex function



, called the complex potential, is defined in

such a way that



izW 

(4.1.12)

Here,

1 i and

z 

. We consider

and

to be functions of z ,

the complex variable, instead of

and y . The physical flow can be pre-

sented with a complex number z in a space, called z-plane.



is an

analytic function, where

and

are conjugate functions, which satisfies

 

Differentiating



zW with respect to z gives the following relationship

wivu



(4.1.13)

where

w is the complex velocity. The conjugate functions

and

sat-

isfy Laplace’ s equation, which is linear. We may be, therefore, able to su-

perimpose solutions

and

for different flows to obtain the new values

and

. In other words, we can superimpose the flows to determine a

new



. This is often put into practice with such that a source, sink, or

potential vortex, or doublet is superimposed onto a uniform flow.

There are typical complex potentials



of some basic flows listed

below:

The relationships, such as given by Eqs. (4.1.10) or (4.1.11) are called

4.1 Potential and Inviscid Flows 119



zUzW

㧘

; real constant. The flow is uniform flow field; (Fig. 4.3(a))

(4.1.14)



zW ln

㧘

q ; real constant. The flow is source





0!q and sink



0q ;

(Fig. 4.3(b))

(4.1.15)



zizW ln

㧘

; circulation, real constant. The flow is potential vortex;

(Fig. 4.3(c))

(4.1.16)



; doublet strength, real constant. The flow is doublet;

(Fig. 4.3(d))

(4.1.17)

  

  

zUzWzWzW

304

U , m and a ; real constants. The flow is flow past a circula

cylinder; (Fig. 4.3(e))

(4.1.18)

There are more complex flow fields to be generated by combination of

those complex potential



. Some schematics are displayed in Fig.

4.3(a–e), which are respectively corresponded to Eqs. (4.1.14–4.1.18).

With a mathematical technique, called a conformal mapping, a simple

flow pattern can be transformed into a more complex one, such as flow

past around a rotating cylinder to airfoils and etc. One of the most known

mapping function is

]

z 

(4.1.19)

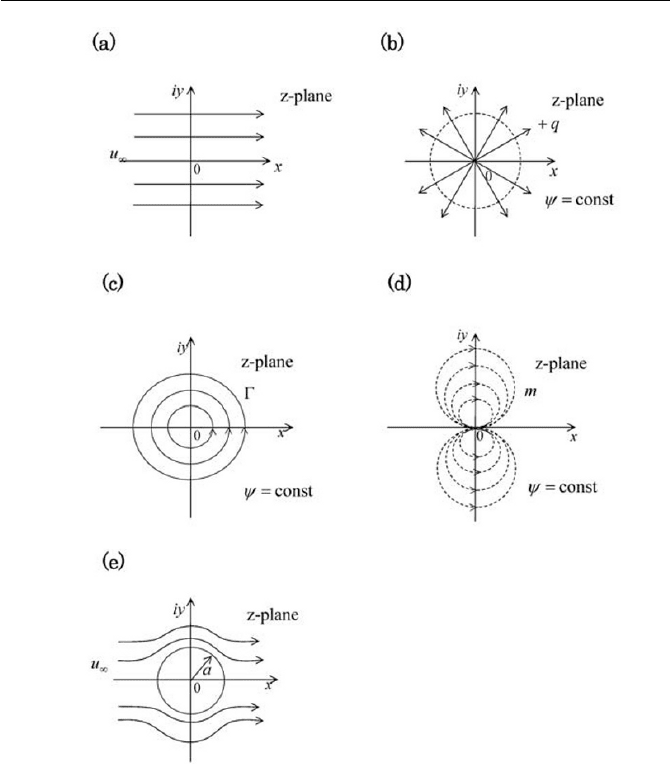
120 4 Perfect Flow

Fig. 4.3 Flow patterns with



Note that

 

yxiyx ,,

[

]

 and a is positive real constant. The map-

ping function given by Eq. (4.1.19) is the Joukowski transformation, which

transforms



of Eq. (4.1.18) into a flow on airfoil, for example. In

general, a mapping function



]

transforms a basic flow in z-plane to

–

[

plane, where the orthogonality of

and

is preserved.

When we consider an inviscid flow, lifting the irrotational condition,

the Navier-Stokes equation reduces to the Euler equation given by Eq.

4.1 Potential and Inviscid Flows 121

(4.2). The Euler equation is often used to investigate compressible flow at

high speed, where viscous and turbulent effects are important only in a

limited region near solid surfaces. With modern computers, flows over an

aircraft may be simulated using Euler equations with which flows do not

stick to walls and slip is allowed at the solid boundaries. Such flow simula-

tions with the aid of computational fluid dynamics (CFD) are being done

on a research basis, and we shall not go too deeply into this field of study,

though these compressible flows will be treated in later chapters in this

text.

Considering the Euler equation, we now look into the most important

theorem in engineering fluid mechanics, Bernoulli’s theorem. The Euler

equation of Eq. (4.2) can be written in general vector form, using vector

identity in the convective term as follows



uu

uuu

(4.1.20)

and

 u

Ȧuu

(4.1.21)

The gravitational force

is assumed here as a conservation force and is

written by a scalar potential as

 g

(4.1.22)

The first integral of the equation can be obtained by integrating Eq.

(4.1.21) between two arbitrary points along a path

, letting ld be a line

element of length along the path

l . We then have

³³³³³

u 





lȦul

llul

dddpdd

(4.1.23)

The third term on the left side of Eq. (4.1.23) contains thermodynamics

properties,

and

, and if we assume that the flow along l is isentropic,

then the relationship between

and



(4.1.24)

From Eq. (4.1.24), the integral can be replaced by the function



³³

 

dpd

(4.1.25)

)