Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)
Подождите немного. Документ загружается.

3.1 Fluid Static 81
Sectional Section area
Second moment of
surface area
bh
12
3
bh
12
hhb
3
1
3
2
12
1
hhb
2
h
12
4
h
2
4
1
d
S
4
64
1
d
S
4
2
1
2
2
dd
S
4
1
4
2
64
1
dd
S
ab
S
4
3
ba
S
bh
2
1
3
36
1
bh
3
32
3
1
he
he
h
b
h
2
h
1
b
hh
d
d
2
d
1
2a
2b
h
e
1
e
2
b
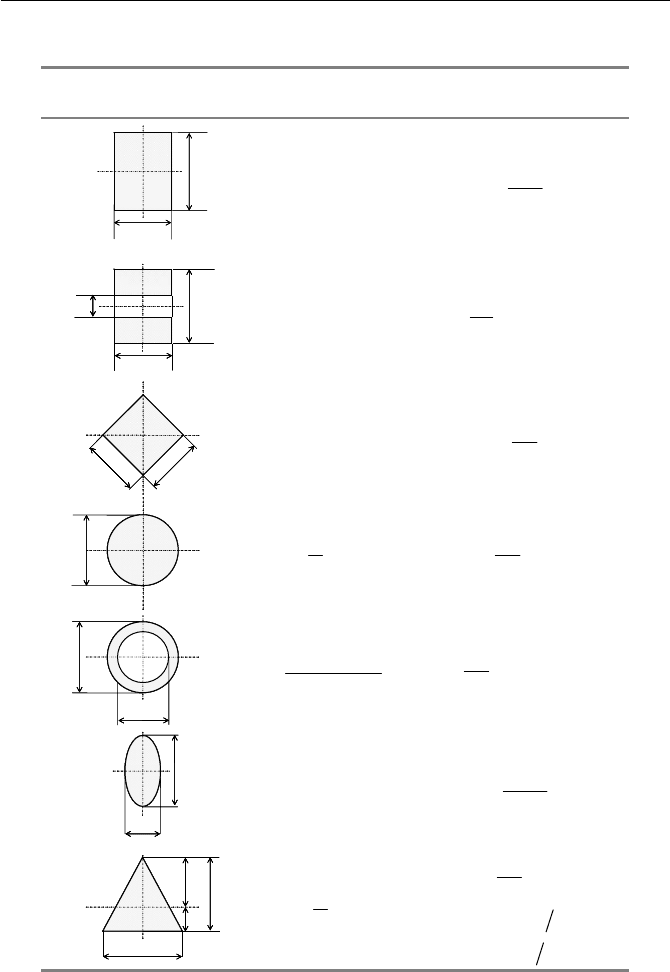
Table 3.1 List of some representative
x
I
c

82 3 Fluid Static and Interfaces
³
³
³
V
S
S
pdV
dSp
pd
closed
closed
n
SF
ˆ
(3.1.25)
(3.1.26)
(3.1.27)
where Eq. (3.1.27) is obtained from Eq. (3.1.26) by applying the Gauss’
divergence theorem. Noting in the hydrodynamic equation given in Eq.
(3.1.2), an inertial reference frame without a rigid body rotation, one can
write
p
as
g
U
p
(3.1.28)
so that Eq. (3.1.27) becomes
³
V
dVg
U
F
(3.1.29)
The gravity acceleration
g
is supposed to be negative for z direction, i.e.
z
e
ˆ
g g
Thus, Eq. (3.1.29) can be straightforwardly written in the simple form
z
V
z
V
dV
e
eF
ˆ
ˆ
g
g
U
U
³
(3.1.30)
Equation (3.1.30) is well-known principle of Archimedes, saying that due
to the vertical force
F
, the weight of an immersed body in a liquid will be
reduced by an amount equal to the weigh of the displaced liquid
Vg
U
, and
the force is called the buoyant force.
Opposite to the situation of the buoyant force, there is a case when a
pressurized fluid (usually a gas) is contained in a vessel, called a pressure
vessel, where the force on the inner wall of the vessel is exerted by the in-
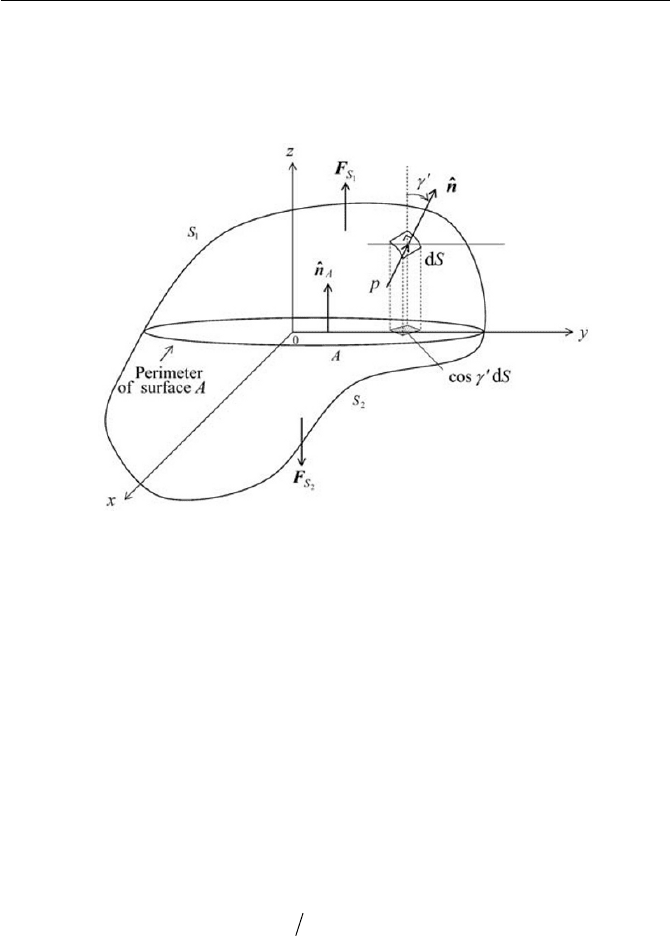
ner pressure, as depicted in Fig. 3.6. Certainly without a body force
g
U
,
the overall force acting on the inner wall of enclosure is zero from an anal-
ogy of Eq. (3.1.27), where
p is zero everywhere in the enclosure. How-
ever, let us examine a partial force on a surface of the enclosure
1
S , which
is cut by an arbitrary plane
A , where the plane A has an unit normal vec-
tor
A
n
ˆ
, and, for brevity’s sake, let us take the local Cartesian coordinates
3.1 Fluid Static 83
system
x
, y , z , i.e.
ZA
en
ˆˆ
as shown in Fig. 3.6. The partial force
1
S
F on
the surface
1
S is calculated with the following formula
Fig. 3.6 Inner pressure on enclosed surface
³
1
1
S
S
dSpnF
ˆ
(3.1.31)
Denoting
zyx
eeen
ˆˆˆˆ
JED
c
c
c
coscoscos
, where
D
c
cos
,
E
c
cos
and
J
c
cos are directional cosines in the local coordinates system, which yields
³
³³³
c
¸
¹
·
¨
©
§
c
c
c
1
111
1
cos
coscoscos
S
z
S
z
S
y
S
xS
dSp
dSdSdSp
e
eeeF
ˆ
ˆˆˆ
J
JED
(3.1.32)
since the integrals of
D
c
and
E
c
involve
SD
d
c
d0 and
SE
d
c
d0
re-
spectively, while
J
c
is
20
SJ
d
c
d for
1
S surface, i.e.
0coscos
11
0
¿
¾
½
¯
®
cc
c
³³³
SS
dSddS
D
S
DDD
(3.1.33a)
84 3 Fluid Static and Interfaces
0coscos
11
0
¿
¾
½
¯
®
cc
c
³³³
SS
dSddS
E
S
EEE
(3.1.33b)
0coscos
11
2
0
z
¿
¾
½
¯
®
cc
c
³³³
SS
dSddS
J
S
JJJ
(3.1.33c)
where
J
E
D
,,rfdS ,
J
D
E
,,rfdS , and
E
D
J
,,rfdS , thus only
z
e
ˆ
term survives. In Eq. (3.1.33c), ds
J
c
cos
is a surface element on the
plane A , which gives
zzS
pApA neF
ˆˆ
1
(3.1.34)
Equation (3.1.34) indicates that the partial force on an arbitrary inner sur-
face
1
S , which is cut by an arbitrary plane A , is equivalent to the force
pA acting on the plane A toward the direction of normal to the plane A .
Similarly for
2
S surface,
zS
pAeF
ˆ
2
would be expected, which bal-
anced as
21
SS
FF , since the overall force on the inner surface is zero.
Usually for a pressure vessel,
1
S
F force is sustained by a wall thickness of
the perimeter of the plane A .
A fluid is still in static equilibrium when the fluid is rotated and accel-
erated in an inertial frame, where each fluid particle in a fluid rotates and
accelerated as if the fluid is a rigid body. From Eq. (3.1.2) the generalized
hydrostatic equation can be expressed in the accelerating reference frame
as
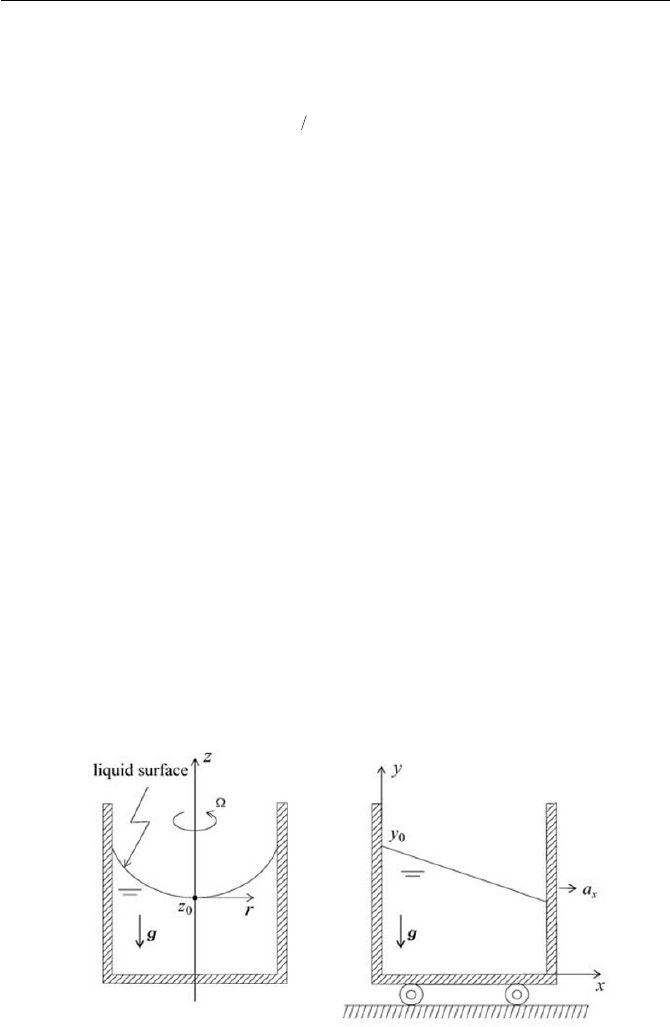
(a) (b)
Fig. 3.7 Liquid in accelerating reference fram
e

3.1 Fluid Static 85
g
U
I
U
r
p a
(3.1.35)
where
2
22
r
I
and
r
a are the relative acceleration of a fluid to the in-
ertial reference frame. This is D’Alembert’s principle, where the reversed
accelerating force in the inertial reference frame can be included as a body
force in dealing with a problem of hydrostatics in an accelerating reference
frame.
In order to illustrate the physical meaning of Eq. (3.1.35), let us con-
sider a situation of a liquid contained in a rotating container, such as shown
in Fig. 3.7(a), assuming that the liquid reaches static equilibrium with re-
spect to the container and the rotating reference frame z
r
. As seen in Fig.
3.7(a), the free surface of the liquid will be curved since the centrifugal
force is acting on a fluid particle, pushing the liquid toward the wall of the
container. The configuration of the static state is called the forced vortex.
In the rotating reference frame z
r
, the pressure distribution in the liquid
is a function of
r
and z so that the differential equation to give the pres-
sure distribution is of the total differentiation of
p
as follows
dz
z
p
dr
r
p
dp
w
w
w
w
(3.1.36)
The partial differentiations of Eq. (3.1.36) are given in Eq. (3.1.35), re-
garding the fact that there is no relative acceleration, i.e. setting 0
r
a
2
U
r
r
p
w
w
(3.1.37)
and
g
U
z
p
(3.1.38)
Thus, Eq. (3.1.36) becomes
dzdrrdp g
U
U
2
(3.1.39)
We can now integrate Eq. (3.1.39) between any two points
00
z,r and
zr, to obtain
:
:
:
86 3 Fluid Static and Interfaces
0
22
0
2
0
22
0
2
1
2
1
zzr
zzrrpp
:
:
g
g
UU
UU
(3.1.40)
where we have set 0
0
r at the center of rotation. In Eq. (3.1.40), we can
see that pressure varies with the square of the radius and a large pressure
difference
0
pp that is created inside the forced vortex. This is the work-
ing principle of a centrifugal pump, where a low pressure liquid is fed into
the center of the rotation, and expelled toward the radius with a higher
pressure. The surface of the forced vortex can be calculated by set-
ting
0
pp , where at the liquid surface pressure is the same as the sur-
rounding pressure (atmospheric pressure
a
p for example if the surface
tension is neglected). Thus, from Eq. (3.1.40), we can obtain the surface
profile
g2
22
0
r
zz
(3.1.41)
revolution.
In the same manner, let us consider another situation, as shown in Fig.
3.7(b), where a fluid in a tank is in static equilibrium relative to the refer-
ence frame, which linearly accelerates toward
x
direction with an accel-
eration component
x
a . Similar to Eq. (3.1.36), we have
dx
y
p
dx
x
p
dp
(3.1.42)
in which
xp ww and yp ww are given in Eq. (3.1.35) as follows
x
a
x
p
U
(3.1.43)
and
g
U
y
p
(3.1.44)
Thus, Eq. (3.1.42) becomes, to obtain
p
in a deferential form
:
It is easily seen from Eq. (3.1.41), that the free surface is a paraboloid of

3.2 Fluid-fluid Interfaces 87
dydxadp
x
g
U
U
(3.1.45)
We can integrate Eq. (3.1.45) between any two points
00
yx , and
yx, to give
0
000
yyxa
yyxxapp
x
x
g
g
UU
U
U
(3.1.46)
where we set
0
0
x at the lower left corner of the tank, as shown in Fig.
3.7(b). With the same thought as considered in Eq. (3.1.41), we can obtain
the shape of the free surface of the liquid as follows
0
yx
a
y
x
g
(3.1.47)
Thus, as verified by Eq. (3.1.47) and sketched in Fig. 3.7(b), the free sur-
face declines linearly toward the direction of the acceleration.
3.2 Fluid-fluid Interfaces
In treating mechanics on the interface of two immiscible fluids, A and B,
the boundary condition is such that
nunu
ˆˆ
BA
(3.2.1)
As such, the interface moves with the same velocities
A
u and
B
u at the in-
terface of fluid A and fluid B respectively.
n
ˆ
denotes the unit normal to the
interface directed from A to B, as shown in Fig. 3.8. A balance of forces,
including inertial and body forces, may be expressed as follows
0
11
¸
¸
¹
·
¨
¨
©
§
c
VVU
nBA
RR
nna
ˆ
TT
ˆ
ൖൕ
g
(3.2.2)
U
c
is the interface density,
V
is the surface tension,
V
n
is the gradient of
V
normal to the interface, a is the acceleration, and g is the gravity accel-
eration (the body force) for the mass of
U
c
.
A
T and
B
T are respectively the
total stress tensor expressed in Eq. (1.6.11), and
ൕ
R and
ൖ
R are the principal
radii of curvature of the interface between fluid A and B. It is mentioned here
that the third term in Eq. (3.2.2) is called the Young-Laplace relationship. Note
that
ൕ
R and
ൖ
R are positive when the corresponding center of curvature is in
fluid A, and vice versa.
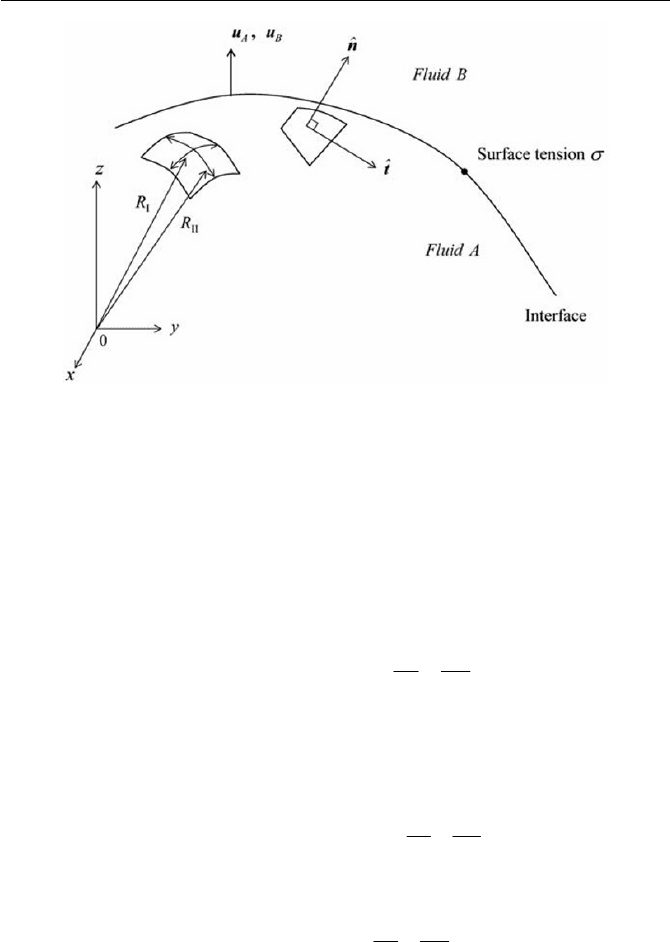
88 3 Fluid Static and Interfaces
Fig. 3.8 Interface of two immiscible fluid
Equation (3.2.2) is rather general, such that the
V
n
term may be-
come important with regard to a film with surfactants, temperature gradi-
ents and when the total stress tensor may include effects from an electro-
magnetic field, and likewise for Eq. (1.6.14). However, without loosing
generality, we can just assume that those effects and terms included in Eq.
(3.2.2) can be neglected, further denoting that the surface density
U
c
is
negligible. So under that assumption, Eq. (3.2.2) can be simply written as
0
11
¸
¹
·
¨
©
§
nnn
A
ˆ
IJI
ˆ
IJI
ˆ
ൖൕ
RR
pp
BB
A
V
(3.2.3)
Equation (3.2.3) gives important stress conditions at the interface, by decom-
posing Eq. (3.2.3) to n
ˆ
– direction and
t
ˆ
– direction, where
t
ˆ
is the unit tan-
gent to the interface. For
n
ˆ
– the direction of the interface, we can write
0
11
¿
¾
½
¯
®
¸
¸
¹
·
¨
¨
©
§
nnnn
ˆ
IJI
ˆ
IJI
ˆˆ
ൖൕ
RR
pp
BBAA
V
So that
0
11
¸
¹
·
¨
©
§
ൖൕ
RR
pp
nn
B
nn
AAB
V
IJIJ
(3.2.4)
Equation (3.2.4) is referred to as the normal stress interface condition. A
pressure discontinuity occurs if the normal components of
A
IJ and
B
IJ to
the interfacial surface (denoting
nn
-suffix) and surface tension are present.
3.2 Fluid-fluid Interfaces 89
For
t
ˆ
– direction of the interface, we can write
0
11
¿
¾
½
¯
®
¸
¹
·
¨
©
§
nnnt
ˆ
IJI
ˆ
IJI
ˆ
ˆ
ൖൕ
RR
pp
BBAA
V
So that we have
0
nt
B
nt
A
IJIJ
(3.2.5)
Equation (3.2.5) implies that the tangential shear stresses of fluid A and
fluid B, denoting the
nt -suffix, are the same at the interface.
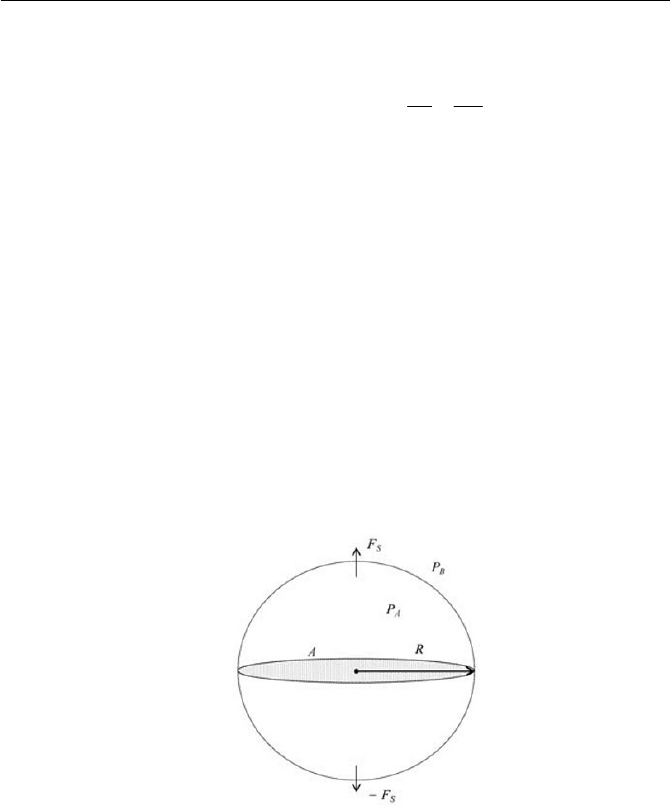
In an application of Eq. (3.2.3), let us consider a specific example of a
bubble in a liquid, as depicted in Fig. 3.9. Denoting that the bubble is in
static equilibrium, where the pressure
A
p of the bubble and
B
p of the sur-
rounding liquid are acting on the spherical surface, and the force due to the
pressure difference is balanced with the surface tension of the two fluids.
We examine the force
S
F as illustrated in Fig. 3.9, due to the inner pres-
sure, acting on the enclosed surface. From Eq. (3.1.34),
S
F is straightfor-
wardly calculated for a sphere as follows
Fig. 3.9 Bubble in static equilibrium
2
RppF
B
A
S
S
(3.2.6)
Considering that
BA
pp ! . This force
S
F is aligned normal to the plane A ,
i.e. the force
S
F is supported at the perimeter of the circle area A due to
the force by the surface tension, which keeps both halves of the sphere to-
gether. Thus,
S
F is equal to the force by the surface tension

90 3 Fluid Static and Interfaces
V
S
RF
S
2
(3.2.7)
Equating Eqs. (3.2.7) and (3.2.6), we can obtain a relationship, that is
R
pp
B
A
V
2
(3.2.8)
Now let us examine the resultant equation of Eq. (3.2.8) from the point
of view of the interfacial force balance at equilibrium. According to the
equation of stress at the interface, Eq. (3.2.3) can be rewritten, assuming
that the bubble is in static equilibrium and implying that there is no motion
in either fluid
A or
B
, i.e. 0
BA
IJIJ , with the condition of
RRR
ൖൕ
for spherical configuration, by
so that it can be reduced to
(3.2.9)
This gives us the same result as Eq. (3.2.8).
Exercise
Exercise 3.1 Micromanometer
Two identical reservoirs, whose cross-sectional area is A , are connected
with a U-tube of cross-sectional area
a , as shown in Fig. 3.10. In the U-
tube a heavy liquid of the density
3
U
is used as a base liquid, with which
the measurement reading of the liquid level takes place. In the reservoir
tanks, there is a lighter immiscible liquid with density
2
U
, which occupies
the remaining portion of the U-tube. Using this arrangement we can meas-
ure the pressure
p
in a vessel, whose density is
1
U
. Assuming one end of
the reservoir tank is opened to the surrounding, such as the atmosphere
a
p
with the density of
0
U
, show the measurement method of this manometer.
R
pp
BA
V
2
nn
ˆˆ
R
pp
BA
V
2
