Yamaguchi H. Engineering Fluid Mechanics (Fluid Mechanics and Its Applications)

Подождите немного. Документ загружается.

70 2 Conservation Equations in Continuum Mechanics

2-6. Obtain a form to calculate the power from Eq. (8) in Exercise 2.3.

Ans.





axis.

aroundrotation flow theof

locity angular ve theiswhich in

Assume

rrmNP

ruru



2-7. In the energy conservation equation, Eq. (2.5.29), if the stress is sym-

metric, write a two-dimensional equation using the Cartesian coordi-

nates system (the

– y plane) assuming the thermal conductivity is

constant, and ignore the internal heat generation.

Ans.





WWWW

u:Ĳ

useand0for

9-BAppendix See

Nomenclature

: pseudovector

321

A,A,A

: components of pseudovector



: diffusive transport of internal angular momentum

: couple stress tensor

: specific heat evaluated at constant pressure

: specific heat evaluated at constant volume

: body force

: gravitational acceleration

: specific enthalpy

: specific kinetic energy

: thermal conductivity

: thermal diffusivity

: external angular momentum

: mass



: mass flow rate

: unit normal (surface direction) vector

: thermodynamic pressure

Bibliography 71



: heat input

: heat flux vector

: specific entropy

Ad ,S

: surface element and surface areas

: total stress tensor

: skew-symmetric part of the tensor

: symmetric part of the tensor

: absolute temperature

: time



: stress vector

: velocity vector

: specific internal energy and

-directional velocity component

: finite volume of fluid particle or control volume

: specific volume (



: work output

: coefficient of thermal expansion

: density

: deviatoric stress

: vorticity

: angular velocity

Bibliography

Conservation laws in continuum mechanics are found in almost all texts. To a

detailed extent, angular momentum conservation and energy conservation are

found in the following texts listed below.

1. A. Rutherford, Vectors, Tensors, and the Basic Equation of Fluid Mechan-

ics, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1962.

2. R. E. Rosensweig, Ferrohydrodynamics, Cambridge University Press,

Cambridge, MA, 1985. Republished from Dover Publications, Inc., 1997.

3. S. M. Richardson, Fluid Mechanics, Hemisphere Publishing Corporation,

New York, 1989.

3. Fluid Static and Interfaces

Now we will look at how the four general conservation laws we developed

in previous chapters can be applied to a great many important engineering

problems when we constitute the system of equations. For many physical

flows in engineering problems, the assumptions of frictionless or inviscid

and incompressible flows allow us to create a reasonably accurate model

representing practical situations.

For the sake of aiding understanding of how to apply the laws we have

just developed in closed systems, we will begin to consider a number of

simpler but still very useful models demonstrated in practical cases.

Fluid static is the simplest case in fluid engineering where the fluid is

at the static state in equilibrium, where the concept of pressure is of par-

ticular importance.

When fluids considered as continuum medium do not involve relative

motion between any parts of the fluid, the state of fluid motion is in static

equilibrium. Without the presence of velocity gradients in static equilib-

rium, the only stress present is the hydrostatic stress, except for in very

specific cases involving non-Newtonian fluids or electromagnetic medium.

The isotropic pressure, which acts normal to the surface of any orientation

of a fluid particle in static equilibrium, is the hydrostatic pressure, which is

identical to the thermodynamic pressure, as verified in Section 2.5.

Fluid static or hydrostatics deals with the mechanics of fluid in static

equilibrium. Fluids in static equilibrium may have common boundaries,

where two single phases are in contact. The pressure discontinuity across

the interface occurs due to surface tension, having the curvature of the in-

terface. This chapter also deals with a basic interfacial phenomenon, which

is often encountered in engineering applications.

3.1 Fluid Static

Let us consider linear momentum conservation with a fluid particle rotat-

ing in an inertial reference frame. From Cauchy's equation of motion,

74 3 Fluid Static and Interfaces

inertial reference frame, given in Eq. (1.2.12), we can write

gua



u Tේ)ේ2(

(3.1.1)

Here

a is the relative acceleration and

u is the relative velocity to the

inertial reference frame. Since in static equilibrium there is no relative mo-

tion of fluid particles,

u can be set identically at zero. The total stress ten-

sor

T can be only written in term of the hydrostatic pressure

, which is

given in Eq. (1.6.11), and the body force

can be regarded as the force

due to gravity

g . Thus, Eq. (3.1.1) can be written as



  p

(3.1.2)

Thus,

 represents the centripetal acceleration and





In applications of hydrostatics, the body force is due to the gravity and

its direction is toward the center of Earth, where we can take the coordi-

nate

z for the positive direction opposite to the gravity as shown in Fig.

3.1. In an inertial reference frame, supposing there would not be rigid-

body rotational acceleration, i.e.

so that 0





and 0

a , Eq.

(3.1.2) can thus be written by the following ordinary differential equation



(3.1.3)

It is noted that

dp is positive when dz is negative, so that the pressure in-

creases when

z decreases, as depicted in Fig. 3.1.

With incompressible flows, we can assume the density

in Eq.

(3.1.3) to be constant. The variation of the pressure

in the z -direction

can be obtained by the integrating Eq. (3.1.3) with respect to

z as follows

zpp g

 

(3.1.4)

where

p is the reference pressure at 0 z . By converting pressure to

equate to the height of a liquid column, Eq. (3.1.4) can be written as

const.



(3.1.5)

given in Eq. (2.2.6), and the acceleration of the fluid particle relative to the

in which is the angular velocity and

is the radius of rotation. Equa-

tion (3.1.2) is the hydrostatic equation, which relates pressure distribution to

acceleration, body force and density.

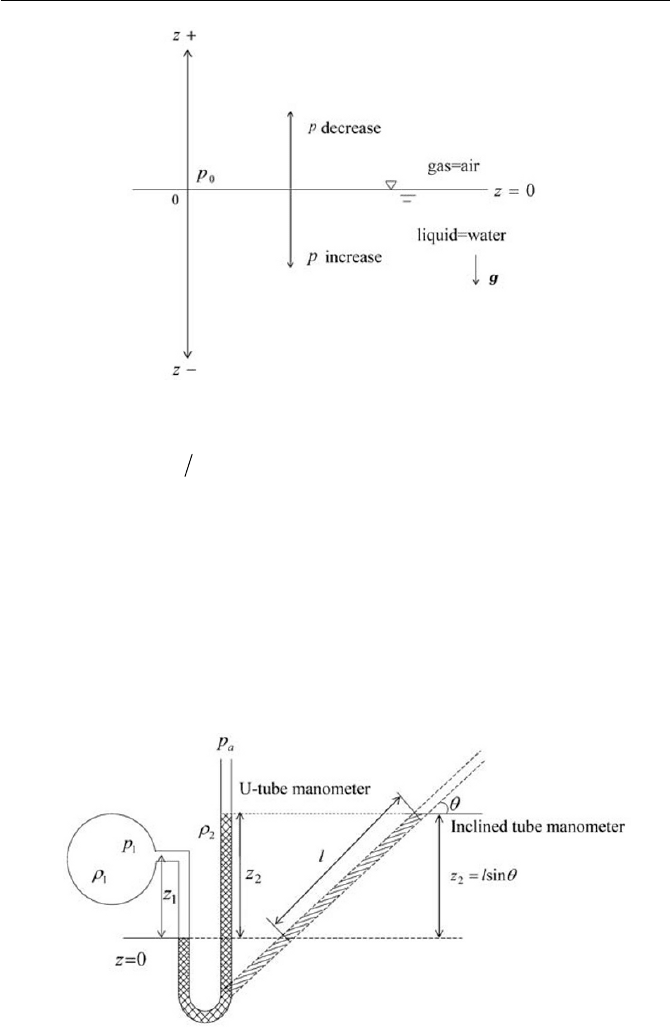
3.1 Fluid Static 75

Fig. 3.1 Coordinate

z a

and pressure

The quantity g

p that appeared in Eq. (3.1.5) is referred to as the

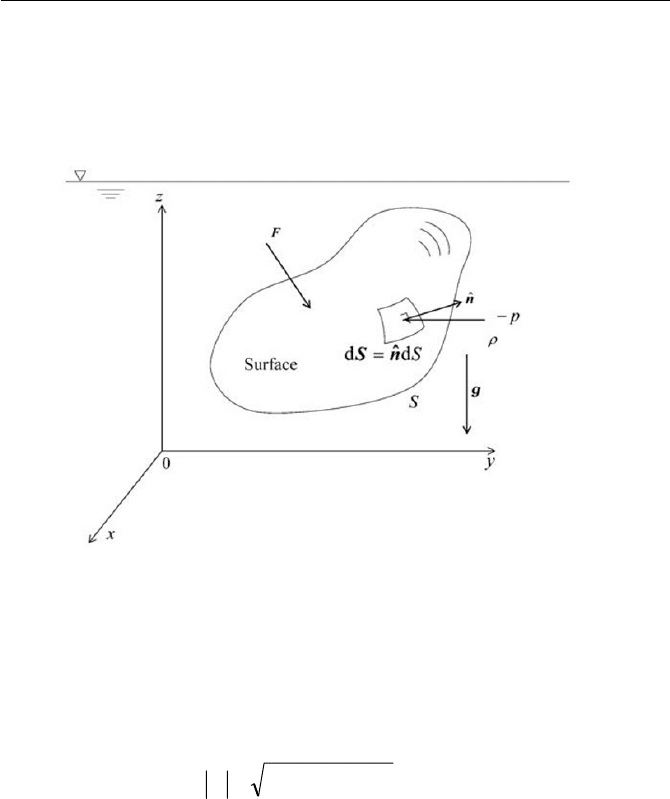
piezometric head. Using columns of liquid, pressures are measured by ma-

nometers. Figure 3.2 shows a U-tube manometer, which may be used to

measure pressure

in a pipe or a vessel containing a fluid of density

The tube contains a liquid of greater density

than that of the metered

fluid. The datum line, from which the liquid columns levels of

z and

are measured, is located at

0 z as shown in Fig. 3.2.

p the atmospheric

pressure acts on the liquid column level of

z side, so that in static equi-

librium of the balance of pressure at the datum line can be written as

Fig. 3.2 U-tube manometer and inclined tube manometer

76 3 Fluid Static and Interfaces

22111

zpzp

 

(3.1.6)

and solving for



pzzp 

11221

(3.1.7)

Thus, according to Eq. (3.1.7), the absolute pressure

p can be measured

by reading the scales of

z and

z . The read pressure (

1122

zz gg

 ) is

referred to as a gauge pressure. It is mentioned that at the vacuum,

p and

will be set zero, with which

z becomes a negative reading to the da-

tum line, metering

z as g

p . For the standard atmospheric pressure,

z is measured via a 760 mm liquid column of mercury; this implies that

mmbar]1013 [

100131 u . [

mN ]. For measuring gas pressure,

is much smaller than

, and Eq. (3.1.7) is simply written where

pzp 

221

(3.1.8)

If the gauge pressure (

) is too small to be read on the scale of

z ,

the liquid column can be inclined, as shown in Fig. 3.2 by the hatched lines.

This arrangement of a manometer is referred to as the inclined tube ma-

nometer, with which the reading of scale l on the tube is taken to give

sin

lz . The inclined tube enables the reading of the scale l to be re-

corded with greater sensitivity.

In engineering design of vessels, dams, water-gate and etc., there are

necessities for calculations of the overall magnitudes and representative

location of forces that act on a submerged plane or curved surface. In the

application of the hydrostatic equation in such engineering problem, we

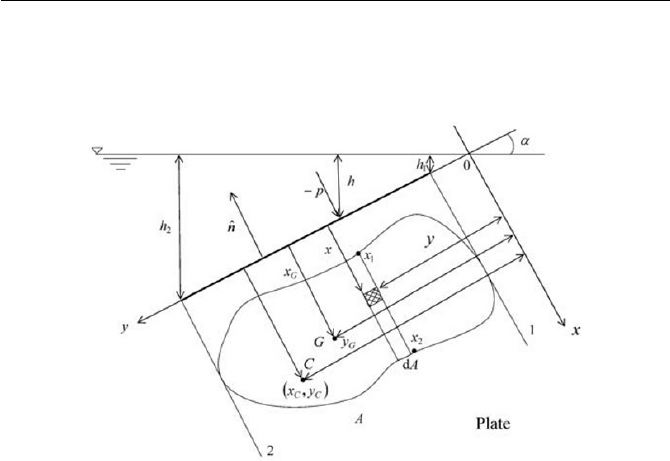
shall consider forces on submerged surfaces. As shown in Fig. 3.3, force

acting on a surface, submerged in a liquid may be obtained by integrat-

ing the pressure

 (the negative sign of

indicates the direction toward

the surface element, while the surface force acts toward the direction to a

unit normal vector

is positive) over the surface as follows



pdSF

(3.1.9)

and



dSpnF

(3.1.10)

3.1 Fluid Static 77

Next let us write the unit normal vector in terms of direction cosines as

l eeeen

ˆˆ

cos

321



(3.1.11)

After considering Eq. (3.1.11), thus Eq. (3.1.10) becomes

Fig. 3.3 Forces on submerged surface

332211

321

eee

eeeeF

ˆˆˆ

ˆˆˆˆ

FFF

pdSpdSpdSdSpl

SSS



 

³³³³

(3.1.12)

and

FFF  F

(3.1.13)

where

and

are the projections of the elementary area Sd on 2–3

(

y – z ), 1–3 (

–

) and 1–2 (

– y ) plane, respectively. Equations. (3.1.12)

and (3.1.13) indicate that the overall magnitude of a force on a curved sur-

face is the vector sum of forces projected on each projection plane.

Consider a simple case, where a flat plate is submerged in a liquid to

the depth of

h and

h from the liquid level. Since the object is flat, we

can take the projection plane for the same direction of

, and we can think

of that the plane as being placed with a constant angle

to the level of the

liquid, as depicted in Fig. 3.4. Hence, for convenience, a local coordinate

78 3 Fluid Static and Interfaces

along the plate surface is taken from a datum coordinate x at the liquid

level. The hydrostatic pressure

on the plate surface at the depth

h

from the liquid level will be easily calculated by Eq. (3.1.4) as

Fig. 3.4 Submerged plate

)( hp  g

(3.1.14)

Here, only the gauge pressure is considered. Thus, the overall force acting

to the plate is





hdA

dAh

(3.1.15)

The integral

dAh

can be calculated with the local coordinates

– y , re-

ferring to Fig. 3.4 as follows

AyydAdAyhdA

 

³³³

DDD

sinsinsin

(3.1.16)

Here,

y is referred to as the centroid,

dydA is the surface element

across the plate, and

A is the total surface area of the plate. Note that

3.1 Fluid Static 79

(

directional centroid) is rather irrelevant since

varies with respect to

h (and consequently to y ). Therefore, Eq. (3.1.15) becomes either



 Ay

sing

(3.1.17)

 g

(3.1.18)

From Eq. (3.1.18), it may be stated that the overall force exerted by a liq-

uid on a static equilibrium is the product of the surface area and the pres-

sure

p at the centroid,

hp g

The representative point on the plate, where the overall force

acts

on the surface, is not at the centroid point, but is referred to as the center of

pressure



C x as shown in Fig. 3.4. The local coordinates

x (

x ,

y )

of the center of pressure

C are obtained by the concept that the moment

balance in the static equilibrium also been halted, as follows

u u

dAp )

( nxFx

(3.1.19)

is given by Eq. (3.1.10). With reference to Fig. 3.4,

x with the local

coordinates (

x ,

y ) can be obtained from

x of Eq. (3.1.19) where

xdFFx and

ydFFy

(3.1.20)

Here,

F is F and dAyhdAdF

singg . Thus, with Eq. (3.1.17),

x and

y can be calculated to give

xydA

and

dAy

(3.1.21)

The integrations in Eq. (3.1.21),

IxydA

and

IdAy

, are

called the product of the surface area

A and the second moment of the

surface area

A (or, alternatively, the product of inertia and the moment of

inertia of the surface area

A ) about

axis respectively. In addition, with

some algebra for the surface

A ,

I and

I are expressed with respect to

the centroid axis parallel to the

and y axes in Fig. 3.4 as follows

GGxyxy

yAxII 

and

Gxx

AyII 

(3.1.22)

80 3 Fluid Static and Interfaces

where

and

are those at the centroid axis. Thus, using the relation-

ship, Eq. (3.1.21) can be further written for

and

where



and



(3.1.23)

In case, for a more simple geometric plate, such as when the plate area is

symmetric about any one of the centroid axis,

becomes zero, so that

the center of pressure is expressed as



GGC

yx ,x

(3.1.24)

This indicates that the overall force acting on the submerged plate is at a

deeper point

y than the position of the centroid

y of the plate. In appli-

cation of further geometric cases of plate, Table 3.1 lists some of represen-

tative

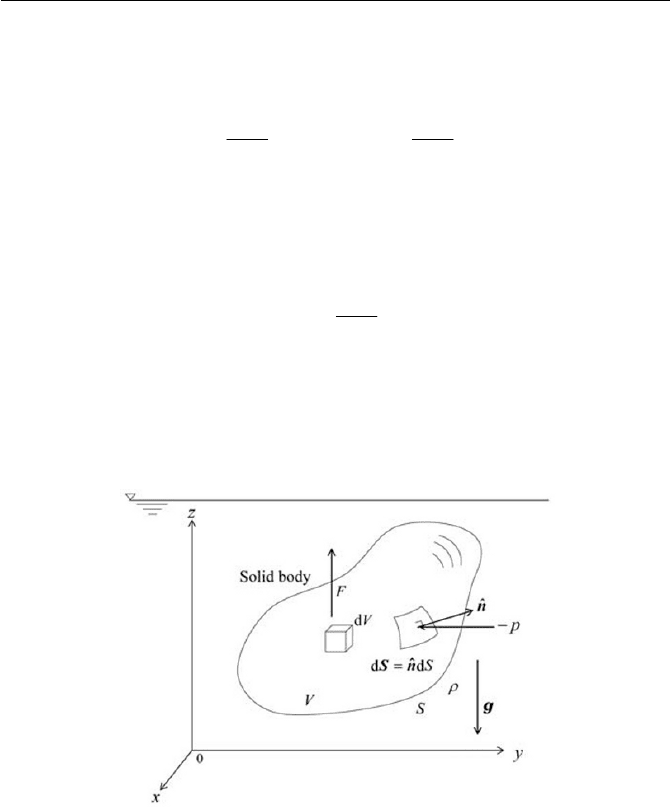
Fig. 3.5 Buoyant force on submerged body

With the same manner, in case of a curved surface, the overall force on

a surface can be obtained as the vector sum of each projected plate, as veri-

fied in Eq. (3.1.12), see Exercise 3.4.

With the extension of forces on submerged surface, we will now con-

sider the force acting on the surface of a solid body immersed in a fluid, as

shown schematically in Fig. 3.5. With the same manner as considered in

Eq. (3.1.9), we take a surface integral over the body where