White R.E. Computational Mathematics: Models, Methods, and Analysis with MATLAB and MPI
Подождите немного. Документ загружается.

1.6. CONVERGENCE ANALYSIS 47
Use the right side of (1.6.8) for
x
w
(nk) in (1.6.10), and combine this with (1.6.9)
to get
H
n+1
g
= x
n+1
x((n + 1)k)
= [
x
n
+ kf(x
vxu
x
n
)]
[x(nk) + f(x
vxu
x(nk))k + x
ww
(f
n+1
)k
2
@2]
=
dH
n
g
+ e
n+1
k
2
@2 (1.6.11)
where
d = 1 fk and e
n+1
= x
ww
(f
n+1
)=
Supp ose d = 1 fk A 0 and |e
n+1
| P. Use the triangle inequality, a
"telescoping" argument and the partial sums of the geometric series 1 +
d +
d
2
+ · · · + d
n
= (d
n+1
1)@(d 1) to get
|H
n+1
g
| d|H
n
g
| + Pk
2
@2
d(d|H
n1
g
| + Pk
2
@2) + Pk
2
@2
.
.
.
d
n+1|
|H
0
g
| + (d
n+1
1)@(d 1) Pk
2
@2= (1.6.12)
Assume H
0
g
= 0 and use the fact that d = 1 fk with k = W@N to ob-
tain
|H
n+1
g
| [(1 fW@N)
N
1]@(fk) Pk
2
@2
1@f Pk@2= (1.6.13)
We have proved the following theorem, which is a special case of a more general
theorem about Euler’s method applied to ordinary di
erential equations of the
Theorem 1.6.3 (Euler Error Theorem) Consider the continuous (1.6.2) and
discrete (1.6.4) Newton cooling models. Let
W be finite, k = W @N and let
solution of (1.6.2) have two derivatives on the time interval [0
> W ]. If the second
derivative of the solution is bounded by
P, the initial condition has no roundo
error and 1 fk A 0, then the discretization error is bounded by (P@2f)k.
In the previous sections we consider discrete models for heat and pollutant
transfer
Pollutant Transfer :
x
w
= i dx
{
fx> (1.6.14)
x(0> w) and x({> 0) given=
Heat Diusion : x
w
= i + (x
{
)
{
fx> (1.6.15)
x(0> w)> x(O> w) and x({> 0) given=
The discretization errors for (1.6.14) and (1.6.15), where the solutions depend
both on space and time, have the form
H
n+1
l
x
n+1
l
x(l{> (n + 1)w)
°
°
H
n+1
°
°
max
l
¯
¯
H
n+1
l
¯
¯
=
© 2004 by Chapman & Hall/CRC
form (1.6.1), see [4,chapter 5.2]
48 CHAPTER 1. DISCRETE TIME-SPACE MODELS
Table 1.6.2: Errors for Flow
t x Flow Errors in (1.6.14)
1/10 1/20 0.2148
1/20 1/40 0.1225
1/40 1/60 0.0658
1/80 1/80 0.0342
Table 1.6.3: Errors for Heat
t x Heat Errors in (1.6.15)
1/50 1/5 9.2079 10
4
1/200 1/10 2.6082 10
4
1/800 1/20 0.6630 10
4
1/3200 1/40 0.1664 10
4
x(l{> (n+ 1)w) i s the exact solution, and x
n+1
l
is the numerical or approximate
solution. In the following examples the discrete models were f rom the explicit
finite dierence methods used in Sections 1.3 and 1.4.
Example for (1.6.14). Consider the M
ATLAB code flow1d.m (see flow1derr.m
and equations (1.4.2-1.4.4)) that generates the numerical solution of (1.6.14)
with f = ghf = =1> d = yho = =1> i = 0> x(0> w) = vlq(2(0 yho w)) and
x({> 0) = vlq(2{). It is compared over the time interval w = 0 to w = W = 20
and at
{ = O = 1 with the exact solution x({> w) = h
ghf w
vlq(2({ yho w)).
Note the error in Table 1.6.2 is proportional to
w + {.
Example for (1.6.15). Consider the M
ATLAB code heat.m (see heaterr.m
and equations (1.2.1)-1.2.3)) that computes the numerical solution of (1.6.15)
with
n = 1@
2
> f = 0> i = 0> x(0> w) = 0> x(1> w) = 0 and x({> 0) = vlq({)= It
is compared at (
{> w) = (1@2> 1) with the exact solution x({> w) = h
w
vlq({).
Here the error in Table 1.6.3 is proportional to
w + {
2
.
In order to give an explanation of the discretization errors, one must use
higher order Taylor polynomial approximation. The proof of this is similar
to the extended mean value theorem. It asserts if
i : [d> e] $ R has q + 1
continuous derivatives on [
d> e], then there is a f between d and { such that
i({) = i(d) + i
(1)
(d)({ d) + · · · + i
(q)
(d)@q! ({ d)
q
+i
(q+1)
(f)@(q + 1)! ({ d)
q+1
=
© 2004 by Chapman & Hall/CRC
1.6. CONVERGENCE ANALYSIS 49
Theorem 1.6.4 (Discretization Error for (1.6.14)) Consider the continuous
model (1.6.14) and its explicit fi nite di
erence model. If d> f and (1dw@{
w f) are nonnegative, and x
ww
and x
{{
are bounded on [0> O]×[0> W ], then there
are constants
F
1
and F
2
such that
°
°
H
n+1
°
°
(F
1
{ + F
2
w)W .
Theorem 1.6.5 (Discretization Error for (1.6.15)) Consider the continuous
model (1.6.15) and its explicit finite di
erence model. If f A 0> A 0> =
(
w@{
2
) and (1 2 w f) A 0, and x
ww
and x
{{{{
are bounded on [0> O] ×
[0
> W ], then there are constants F
1
and F
2
such that
°
°
H
n+1
°
°
(F
1
{
2
+ F
2
w)W=
1.6.7 Exercises
1.
when
pd{n = 80.
2.
pd{n = 80.
3. Assume the surrounding temperature initially is 70 and increases at a
constant rate of one degree every ten minutes.
(a). Modify the continuous model in (1.6.2) and find its solution via the
M
ATLA B command desolve.
(b). Modify the discrete model in (1.6.4).
4. Consider the time dependent surrounding temperature in problem 3.
(a). Modify the MATLAB code eulerr.m to account for the changing
surrounding temperature.
(b). Experiment with di
erent number of time steps with pd{n = 5, 10,
20, 40 and 80.
5. In the proof of the Theorem 1.6.3 justify the (1.6.11) and |
e
n+1
| P.
6. In the proof of the Theorem 1.6.3 justify the (1.6.12) and (1.6.13).
7. Modify Theorem 1.6.3 to account for the case where the surrounding
temperature can depend on time,
x
vxu
= x
vxu
(w). What assumptions should be
placed on
x
vxu
(w) so that the discretization error will be bounded by a constant
times the step size?
8. Modify flow1d.m by inserting
an additional line inside the time-space loops for the error (see flow1derr.m).
9.
additional line inside the time-space loops for the error (see heaterr.m).
10. Consider a combined model for (1.6.14)-(1.6.15):
x
w
= i + (x
{
)
{
dx
{
fx= Formulate suitable boundary conditions, an explicit finite dierence
method, a M
AT LAB code and prove an error estimate.
© 2004 by Chapman & Hall/CRC
Verify the calculations in Table 1.6.1, and find the error when
Verify the computations in Table 1.6.14.
Verify the computations in Table 1.6.15. Modify heat.mbyinserting an
Duplicate the calculations in Figure 1.6.1, and find the graphical solution
Chapter 2
Steady State Discrete
Models
This chapter considers the steady state solution to the heat diusion model.
Here boundary conditions that have derivative terms in them are applied to the
co oling fin model, which will be extended to two and three space variables in
the next two chapters. Variations of the Gauss elimination method are studied
in Sections 2.3 and 2.4 where the block structure of the coe
!cient matrix is
utilized. This will be very imp ortant for parallel solution of large algebraic
systems. The last two sections are concerned with the analysis of two types
of convergence: one with respect to discrete time and one with respect to the
mesh size. Additional introductory references include Burden and Faires [4]
and Meyer [16].
2.1 Steady State and Triangular Solves
2.1.1 Intro duction
The next four sections will be concerned with solving the linear algebraic system
D{ = g (2.1.1)
where
D is a given q × q matrix, g is a given column vector and { is a column
vector to be found. In this section we will focus on the special case where
D is a triangular matrix. Algebraic systems have many applications such as
inventory management, electrical circuits, the steady state polluted stream and
heat di
usion in a wire.
Both the polluted stream and heat diusion problems initially were formu-
lated as time and space dependent problems, but for larger times the concentra-
tions or temperatures depend less on time than on s pace. A time independent
solution is called st eady state or equilibrium solution, which can be modeled by
51
© 2004 by Chapman & Hall/CRC
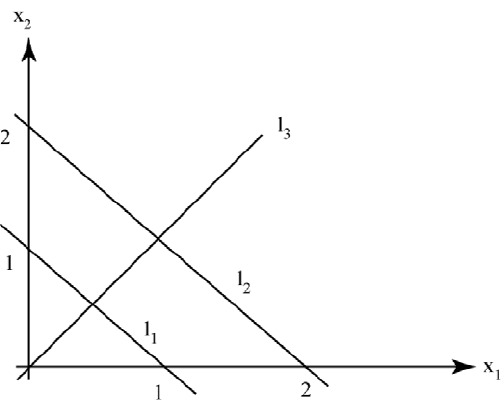
52 CHAPTER 2. STEADY STATE DISCRETE MODELS
Figure 2.1.1: Infinite or None or One Solution(s)
systems of algebraic equations (2.1.1) with
{ being the steady state solution.
Systems of the form
D{ = g can be derived from x = Dx+e via (L D)x = e and
replacing x by {> e by g and (L D) by D.
There are several cases of (2.1.1), which are illustrated by the following
examples.
Example 1. The algebraic system may not have a solution. Consider
1 1
2 2
¸
=
g
1
g
2
¸
=
If g = [1 2]
W
, then there are an infinite number of solutions given by points on
the line l
1
in Figure 2.1.1. If g = [1 4]
W
, then there are no solutions because
the lines l
1
and l
2
are parallel. If the problem is modified to
1 1
2 2
¸
=
1
0
¸
>
then there will be exactly one solution given by the intersection of lines l
1
and
l
3
.
Example 2. This example illustrates a system with three equations with either
no solution or a set of solutions that is a straight line in 3D space.
5
7
1 1 1
0 0 3
0 0 3
6
8
5
7
{
1
{
2
{
3
6
8
=
5
7
1
g
2
3
6
8
If g
2
6= 3, then the second row or equation implies 3{
3
6= 3 and {
1
6= 1. This
contradicts the third row or equation, and hence, there is no solution to the
© 2004 by Chapman & Hall/CRC
2.1. STEADY STATE AND TRIANGULAR SOLVES 53
system of equations. If
g
2
= 3, then {
3
= 1 and {
2
is a free parameter. The
first row or equation is
{
1
+ {
2
+ 1 = 1 or {
1
= {
2
= The vector form of the
solution is
5
7
{
1
{
2
{
3
6
8
=
5
7
0
0
1
6
8
+ {
2
5
7
1
1
0
6
8
=
This is a straight line in 3D space containing the point [0 0 1]
W
and going in
the direction [
1 1 0]
W
.
The easiest algebraic systems to solve have either diagonal or a triangular
matrices.
Example 3. Consider the case where
D is a diagonal matrix.
5
7
1 0 0
0 2 0
0 0 3
6
8
5
7
{
1
{
2
{
3
6
8
=
5
7
1
4
7
6
8
whose solution is
5
7
{
1
{
2
{
3
6
8
=
5
7
1@1
4@2
7
@3
6
8
=
Example 4. Consider the case where A is a lower triangular matrix.
5
7
1 0 0
1 2 0
1 4 3
6
8
5
7
{
1
{
2
{
3
6
8
=
5
7
1
4
7
6
8
=
The first row or equation gives {
1
= 1. Use this in the second row or equation
to get 1 + 2{
2
= 4 and {
2
= 3@2= Put these two into the third row or equation
to get 1(1) + 4(3
@2) + 3{
3
= 7 and {
3
= 0. This is known as a forward sweep.
Example 5. Consider the case where A is an upper triangular matrix
5
7
1 1 1
0 2 2
0 0 3
6
8
5
7
{
1
{
2
{
3
6
8
=
5
7
1
4
9
6
8
=
First, the last row or equation gives {
3
= 3. Second, u se this in the second
row or equation to get 2
{
2
+ 2(3) = 4 and {
2
= 1= Third, put these two into
the first row or equation to get 1({
1
) 1(1) + 3(3) = 1 and {
1
= 9. This
illustrates a backward sweep where the components of the matrix are retrieved
by rows.
2.1.2 Applied Area
Consider a stream which initially has an industrial spill upstream. Suppose
that at the farthest point upstream the river is being polluted so that the
concentration is independent of time. Assume the flow rate of the stream i s
known and the chemical decay rate of the pollutant is known. We would like
© 2004 by Chapman & Hall/CRC
54 CHAPTER 2. STEADY STATE DISCRETE MODELS
to determine the short and long term e
ect of this initial spill and upstream
pollution.
The discrete model was developed in Section 1.4 for the concentration
x
n+1
l
approximation of x(l{> (n + 1)w)).
x
n+1
l
= yho (w@{)x
n
l1
+ (1 yho (w@{) w ghf)x
n
l
l = 1> ===> q 1 and n = 0> ===> pd{n 1>
x
0
l
= given for l = 1> ===> q 1 and
x
n
0
= given for n = 1> ===> pd{n=
This discrete model should approximate the solution to the continuous space
and time model
x
w
= yho x
{
ghf x>
x({> 0) = given and
x(0> w) = given=
The steady state solution will be independent of time. For the discrete model
this is
0 =
yho (w@{)x
l1
+ (0 yho (w@{) w ghf)x
l
(2.1.2)
x
0
= given. (2.1.3)
The discrete steady state model may be reformulated as in (2.1.1) where
D is
a lower triangular matrix. For example, if there are 3 unknown concentrations,
then (2.1.2) must hold for
l = 1> 2> and 3
0 =
yho (w@{)x
0
+ (0 yho (w@{) w ghf)x
1
0 = yho (w@{)x
1
+ (0 yho (w@{) w ghf)x
2
0 = yho (w@{)x
2
+ (0 yho (w@{) w ghf)x
3
=
Or, when g = yho@{ and f = 0 g ghf, the vector form of this is
5
7
f
0 0
g f 0
0 g f
6
8
5
7
x
1
x
2
x
3
6
8
=
5
7
gx
0
0
0
6
8
=
(2.1.4)
If the velocity of the stream is negative so that the stream is moving from right
to left, then x(O> w) will be given and the resulting steady state discrete mo del
will be upper triangular.
The continuous steady state model is
0 =
yho x
{
ghf x> (2.1.5)
x(0) = given. (2.1.6)
The solution is
x({) = x(0)h
(ghf@yho){
= If the velocity of the steam is
negative (moving from the right to the left), then the given concentration will
be
x
q
where q is the size of matrix and the resulting matrix will be upper
triangular.
© 2004 by Chapman & Hall/CRC
2.1. STEADY STATE AND TRIANGULAR SOLVES 55
2.1.3 Model
The general model will be an algebraic system (2.1.1) of q equations and q
unknowns. We will assume the matrix has upper triangular form
D = [d
lm
] where d
lm
= 0 for l A m and 1 l> m q=
The row numbers of the matrix are associated with i, and the column numbers
are given by
m. The component form of D{ = g when D is upper triangular is
for all i
d
ll
{
l
+
X
mAl
d
lm
{
m
= g
l
= (2.1.7)
One can take advantage of this by setting
l = q, where the summation is now
vacuous, and solve for
{
q
=
2.1.4 Method
The last equation in the component form is d
qq
{
q
= g
q
, and hence, {
q
=
g
q
@d
qq
. The (q 1) equation is d
q1>q1
{
q1
+ d
q1>q
{
q
= g
q1
, and hence,
we can solve for
{
q1
= (g
q1
d
q1>q
{
q
)@d
q1>q1=
This can be repeated,
provided each
d
ll
is nonzero, until all {
m
have been computed. In order to
execute this on a computer, there mus t be two loops: one for the equation
(2.1.7) (the i-loop) and one for the summation (the j-loop). There are two
versions: the ij version with the i-loop on the outside, and the ji version with
the j-loop on the outside. The ij version is a reflection of the backward sweep
as in Example 5. Note the inner loop retrieves data from the array by jumping
from one column to the next. In Fortran this is in stride
q and can result
in slower computation times. Example 6 illustrates the ji version where we
subtract multiples of the columns of D, the order of the loops is interchanged,
and the components of D are retrieved by moving down the columns of D.
Example 6. Consider the following 3 × 3 algebraic system
5
7
4 6 1
0 1 1
0 0 4
6
8
5
7
{
1
{
2
{
3
6
8
=
5
7
100
10
20
6
8
=
This product can also be viewed as linear combinations of the columns of the
matrix
5
7
4
0
0
6
8
{
1
+
5
7
6
1
0
6
8
{
2
+
5
7
1
1
4
6
8
{
3
=
5
7
100
10
20
6
8
=
First, solve for {
3
= 20@4 = 5. Second, subtract the last column times {
3
from
both sides to reduce the dimension of the problem
© 2004 by Chapman & Hall/CRC
56 CHAPTER 2. STEADY STATE DISCRETE MODELS
5
7
4
0
0
6
8
{
1
+
5
7
6
1
0
6
8
{
2
=
5
7
100
10
20
6
8
5
7
1
1
4
6
8
5 =
5
7
95
5
0
6
8
=
Third, solve for {
2
= 5@1. Fourth, subtract the second column times {
2
from
both sides
5
7
4
0
0
6
8
{
1
=
5
7
95
5
0
6
8
5
7
6
1
0
6
8
5 =
5
7
65
0
0
6
8
=
Fifth, solve for {
1
= 65@4.
Since the following M
AT LAB co des for the ij and ji methods of an upper
triangular matrix solve are very clear, we will not give a formal statement of
these two methods.
2.1.5 Implementation
We illustrate two MATLAB codes for doing upper triangular solve with the ij
(row) and the ji (column) methods. Then the M
ATLAB solver { = D\g and
lqy(D) g will be used to solve the steady state polluted stream problem.
In the code jisol.m lines 1-4 are the data for Example 6, and line 5 is the first
step of the column version. The j-loop in line 6 moves the rightmost column of
the matrix to the right side of the vector equation, and then in line 10 the next
value of the solution is computed.
MATLAB Code jisol.m
1. clear;
2. A = [4 6 1;0 1 1;0 0 4]
3. d = [100 10 20]’
4. n = 3
5. x(n) = d(n)/A(n,n);
6. for j = n:-1:2
7. for i = 1:j-1
8. d(i) = d(i) - A(i,j)*x(j);
9. end
10. x(j-1) = d(j-1)/A(j-1,j-1);
11. end
12. x
In the code ijsol.m the i-loop in line 6 computes the partial row sum with
respect to the
m index, and this is done for each row l by the j-loop in line 8.
MATLAB Code ijsol.m
1. clear;
2. A = [4 6 1;0 1 1;0 0 4]
© 2004 by Chapman & Hall/CRC
2.1. STEADY STATE AND TRIANGULAR SOLVES 57
3. d = [100 10 20]’
4. n = 3
5. x(n) = d(n)/A(n,n);
6. for i = n:-1:1
7. sum = d(i);
8. for j = i+1:n
9. sum = sum - A(i,j)*x(j);
10. end
11. x(i) = sum/A(i,i);
12. end
13. x
M
ATLA B can easily solve problems with q equations and q unknowns, and
the coe!cient matrix, D, does not have to be either upper or lower triangular.
The following are two commands to do this, and these will be more completely
described in the next section.
MATLAB Linear Solve A\d and inv(A)*d.
AA
A =
4 6 1
0 1 1
0 0 4
Ad
d =
100
10
20
Ax = A\d
x =
16.2500
5.0000
5.0000
Ax = inv(A)*d
x =
16.2500
5.0000
5.0000
Finally, we return to the steady state polluted stream in (2.1.4). Assume
O = 1, { = O@3 = 1@3, yho = 1@3, ghf = 1@10 and x(0) = 2@10. The
continuous steady state solution is
x({) = (2@10)h
(3@10){
. We approximate
this solution by either the discrete solution for large k, or the solution to the
algebraic system. For just three unknowns the algebraic system in (2.1.4) with
© 2004 by Chapman & Hall/CRC
