White R.E. Computational Mathematics: Models, Methods, and Analysis with MATLAB and MPI
Подождите немного. Документ загружается.


58 CHAPTER 2. STEADY STATE DISCRETE MODELS
g = (1@3)@(1@3) = 1 and f = 0 1 (1@10) = 1=1 is easily solved for the
approximate concentration at three positions in the stream.
AA = [1.1 0 0;-1 1.1 0;0 -1 1.1]
A =
1.1000 0 0
-1.0000 1.1000 0
0 -1.0000 1.1000
Ad = [.2 0 0]’
d =
0.2000
0
0
AA\d
ans =
0.1818
0.1653
0.1503
The above numerical solution is an approximation of continuous solution
x({) = =2h
{
where {
1
= 1{ = 1@3, {
2
= 2{ = 2@3 and {
3
= 3{ = 1 so
that
=2h
=1
= =18096, =2h
=2
= =16375 and =2h
=3
= =14816, respectively.
2.1.6 Assessment
One problem with the upper triangular solve algorithm may occur if the di-
agonal components of
D, d
ll
, are very small. In this case the floating point
approximation may induce significant errors. Another instance is two equations
which are nearly the same. For example, for two equations and two variables
suppose the lines associated with the two equations are almost parallel. Then
small changes in the slopes, given by either floating point or empirical data ap-
proximations, will induce big changes in the location of the intersection, that is,
the solution. The following elementary theorem gives conditions on the matrix
that will yield unique solutions.
Theorem 2.1.1 (Upper Triangular Existence) Consider
D{ = g where D is
upper triangular (
d
lm
= 0 for i A j) and an q × q matrix. If all d
ll
are not zero,
then
D{ = g has a solution. Moreover, this solution is unique.
Proof. The derivation of the ij method for solving upper triangular algebraic
systems established the existence part. In order to prove the solution is unique,
let
{ and | be two solutions D{ = g and D| = g. Subtract these two and use the
distributive property of matrix products
D{ D| = g g so that D({ |) = 0.
Now apply the upper triangular solve algorithm with
g replaced by 0 and {
replaced by { |. This implies { | = 0 and so { = |.
© 2004 by Chapman & Hall/CRC
2.2. HEAT DIFFUSION AND GAUSS ELIMINATION 59
2.1.7 Exercises
1. State an ij version of an algorithm for solving lower triangular problems.
2. Prove an analogous existence and uniqueness theorem for lower triangular
problems.
3. Use the ij version to solve the following
5
9
9
7
1 0 0 0
2 5 0 0
1 4 5 0
0 2 3
2
6
:
:
8
5
9
9
7
{
1
{
2
{
3
{
4
6
:
:
8
=
5
9
9
7
1
3
7
11
6
:
:
8
=
4. Consider example 5 and use example 6 as a guide to formulate a ji (col-
umn) version of the solution for example 5.
5. Use the ji version to solve the problem in 3.
6. Write a M
AT LAB version of the ji method for a lower triangular solve.
Use it to solve the problem in 3.
7. Use the ij version and M
ATLA B to solve the problem in 3.
8. Verify the calculations for the polluted stream problem. Experiment with
di
erent flow and decay rates. Observe stability and steady state solutions.
9. Consider the steady state polluted stream problem with fixed
O = 1=0,
yho = 1@3 and ghf = 1@10. Experiment with 4, 8 and 16 unknowns so that
{ = 1@4> 1@8 and1/16, respectively. Formulate the analogue of the vector
equation (2.1.14) and solve it. Compare the solutions with the solution of the
continuous model.
10. Formulate a discrete model for the polluted stream problem when the
velocity of the stream is negative.
2.2 Heat Diusion and Gauss Elimination
2.2.1 Intro duction
In most applications the coe!cient matrix is not upper or lower triangular. By
adding and subtracting multiples of the equations, often one can convert the
algebraic system into an equivalent triangular system. We want to make this
systematic so that these calculations can be done on a computer.
A first step is to reduce the notation burden. Note that the positions of
all the
{
l
were always the same. Henceforth, we will simply delete them. The
entries in the
q × q matrix D and the entries in the q × 1 column vector g may
be combined into the
q × (q + 1) augmented matrix
[
D g].
For example, the augmented matrix for the algebraic system
© 2004 by Chapman & Hall/CRC
60 CHAPTER 2. STEADY STATE DISCRETE MODELS
2
{
1
+ 6{
2
+ 0{
3
= 12
0
{
1
+ 6{
2
+ 1{
3
= 0
1
{
1
1{
2
+ 1{
3
= 0
is
[
D g] =
5
7
2 6 0 12
0 6 1 0
1 1 1 0
6
8
=
Each row of the augmented matrix represents the coe!cients and the right side
of an equation in the algebraic system.
The next step is to add or subtract multiples of rows to get all zeros in the
lower triangular part of the matrix. There are three basic row operations:
(i). interchange the order of two rows or equations,
(ii). multiply a row or equation by a nonzero constant and
(iii). add or subtract rows or equations.
In the following example we use a combination of (ii) and (iii), and note each row
operation is equivalent to a multiplication by an elementary matrix, a matrix
with ones on the d iagonal and one nonzero o
-diagonal component.
Example. Consider the above problem. First, subtract 1/2 of row 1 from row
3 to get a zero in the (3,1) position:
H
1
[D g] =
5
7
2 6 0 12
0 6 1 0
0
4 1 6
6
8
where H
1
=
5
7
1 0 0
0 1 0
1@2 0 1
6
8
=
Second, add 2/3 of row 2 to row 3 to get a zero in the (3,2) position:
H
2
H
1
[D g] =
5
7
2 6 0 12
0 6 1 0
0 0 5
@3 6
6
8
where H
2
=
5
7
1 0 0
0 1 0
0 2
@3 1
6
8
=
Let H = H
2
H
1
> X = HD and
b
g = Hg so that H[D g] = [X
b
g]= Note X is upper
triangular. Each elementary row operation can be reversed, and this has the
form of a matrix inverse of each elementary matrix:
H
1
1
=
5
7
1 0 0
0 1 0
1@2 0 1
6
8
and H
1
1
H
1
= L =
5
7
1 0 0
0 1 0
0 0 1
6
8
>
H
1
2
=
5
7
1 0 0
0 1 0
0
2@3 1
6
8
and H
1
2
H
2
= L=
Note that D = OX where O = H
1
1
H
1
2
because by repeated use of the associa-
© 2004 by Chapman & Hall/CRC
2.2. HEAT DIFFUSION AND GAUSS ELIMINATION 61
tive property
(
H
1
1
H
1
2
)(HD) = (H
1
1
H
1
2
)((H
2
H
1
)D)
= ((
H
1
1
H
1
2
)(H
2
H
1
))D
= (H
1
1
(H
1
2
(H
2
H
1
)))D
= (H
1
1
((H
1
2
H
2
)H
1
))D
= (H
1
1
H
1
)D
= D=
The product O = H
1
H
2
is a lower triangular matrix and D = OX is called an
OX factorization of D.
Definition. An
q × q matrix, A, has an inverse q × q matrix, D
1
, if and
only if D
1
D = DD
1
= L, the q × q identity matrix.
Theorem 2.2.1 (Basic Properties) Let
D be an q × q matrix that has an in-
verse:
1.
D
1
is unique,
2.
{ = D
1
g is a solution to D{ = g>
3. (DE)
1
= E
1
D
1
provided E also has an inverse and
4.
D
1
=
£
f
1
f
2
· · · f
q
¤
has column vectors that are solutions to
Df
m
= h
m
where h
m
are unit column vectors with all zero components except
the j
wk
, which is equal to one.
We will later discuss these properties in more detail. Note, given an inverse
matrix one can solve the associated linear system. Conversely, if one can solve
the linear problems in property 4 via Gaussian elimination, then one can fi nd the
inverse matrix. Elementary matrices can be used to find the
OX factorizations
and the inverses of
O and X. Once O and X are known apply property 3 to find
D
1
= X
1
O
1
more details. Not all matrices have inverses such as
D =
1 0
2 0
¸
=
Also, one may need to use permutations of the rows of D so that S D = OX
such as
D =
0 1
2 3
¸
S D =
0 1
1 0
¸
0 1
2 3
¸
=
2 3
0 1
¸
=
© 2004 by Chapman & Hall/CRC
.Aword of caution is appropriate and also see Section 8.1 for
62 CHAPTER 2. STEADY STATE DISCRETE MODELS
2.2.2 Applied Area
We return to the heat conduction problem in a thin wire, which is thermally
insulated on its lateral surface and has length
O. Earlier we used the explicit
method for this problem where the temperature depended on both time and
space. In our calculations we observed, provided the stability condition held,
the time dependent solution converges to time independent solution, which we
called a steady state solution.
Steady state solutions correspond to models, which are also derived from
Fourier’s heat law. The di
erence now is that the change, with respect to time,
in the heat content is zero. Also, the temperature is a function of just space so
that
x
l
x(lk) where k = O@q.
change in heat content = 0
(heat from the source)
+(heat di
usion from the left side)
+(heat di
usion from the right side)=
Let D be the cross section area of the thin wire and N be the thermal conduc-
tivity so that the approximation of the change in the heat content for the small
volume
Dk is
0 =
Dk wi + Dw N(x
l+1
x
l
)@k Dw N(x
l
x
l1
)@k= (2.2.1)
Now, divide by
Dk w , let = N@k
2
, and we have the following q 1 equations
for the q 1 unknown approximate temperatures x
l
=
Finite Dierence Equations for Steady State Heat Diusion.
0 =
i + (x
l+1
+ x
l1
) 2x
l
where (2.2.2)
l = 1> ===> q 1 and = N@k
2
and
x
0
= x
q
= 0= (2.2.3)
Equation (2.2.3) is the temperature at the left and right ends set equal to
zero. The discrete model (2.2.2)-(2.2.3) is an approximation of the continuous
model (2.2.4)-(2.2.5). The partial di
erential equation (2.2.4) can be derived
from (2.2.1) by replacing
x
l
by x(lk)> dividing by Dk w and letting k and w
go to zero.
Continuous Model for Steady State Heat Di
usion.
0 =
i + (Nx
{
)
{
and (2.2.4)
x(0) = 0 = x(O)= (2.2.5)
2.2.3 Model
The finite dierence model may be written in matrix form where the matrix is
a tridiagonal matrix. For example, if
q = 4, then we are dividing the wire into
© 2004 by Chapman & Hall/CRC
2.2. HEAT DIFFUSION AND GAUSS ELIMINATION 63
four equal parts and there will be 3 unknowns with the end temperatures set
equal to zero.
Tridiagonal Algebraic System with n = 4.
5
7
2 0
2
0 2
6
8
5
7
x
1
x
2
x
3
6
8
=
5
7
i
1
i
2
i
3
6
8
=
Suppose the length of the wire is 1 so that k = 1@4, and the thermal conductivity
is .001. Then
= =016 and if i
l
= 1, then upon dividing all rows by and
using the augmented matrix notation we have
[
D g] =
5
7
2 1 0 62=5
1 2 1 62=5
0
1 2 62=5
6
8
=
Forward Sweep (put into upper triangular form):
Add 1/2(row 1) to (row 2),
H
1
[D g] =
5
7
2 1 0 62=5
0 3
@2 1 (3@2)62=5
0
1 2 62=5
6
8
where H
1
=
5
7
1 0 0
1
@2 1 0
0 0 1
6
8
=
Add 2/3(row 2) to (row 3),
H
2
H
1
[D g] =
5
7
2 1 0 62=5
0 3
@2 1 (3@2)62=5
0 0 4@3 (2)62=5
6
8
where H
2
=
5
7
1 0 0
0 1 0
0 2
@3 1
6
8
=
Backward Sweep (solve the triangular system):
x
3
= (2)62=5(3@4) = 93=75>
x
2
= ((3@2)62=5 + 93=75)(2@3) = 125 and
x
1
= (62=5 + 125)@2 = 93=75=
The above solutions of the discrete model should be an approximation of
the continuous model
x({) where { = 1{> 2{ and 3{. Note the OX fac-
torization of the 3 × 3 coe!cient D has the form
D = (H
2
H
1
)
1
X
= H
1
1
H
1
2
X
=
5
7
1 0 0
1@2 1 0
0 0 1
6
8
5
7
1 0 0
0 1 0
0
2@3 1
6
8
5
7
2 1 0
0 3
@2 1
0 0 4@3
6
8
=
5
7
1 0 0
1@2 1 0
0 2@3 1
6
8
5
7
2 1 0
0 3
@2 1
0 0 4@3
6
8
= OX=
© 2004 by Chapman & Hall/CRC
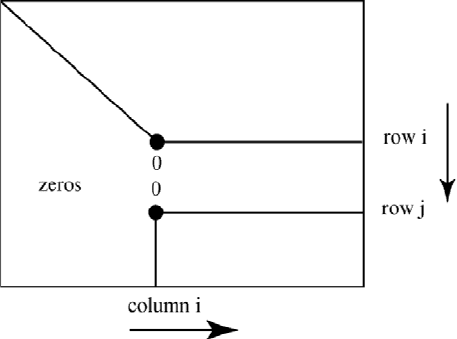
64 CHAPTER 2. STEADY STATE DISCRETE MODELS
Figure 2.2.1: Gaussian Elimination
2.2.4 Method
The general Gaussian elimination method requires forming the augmented ma-
trix, a forward sweep to convert the problem to upper triangular form, and
a backward sweep to solve this upper triangular system. The row operations
needed to form the upper triangular system must be done in a systematic way:
(i). Start with column 1 and row 1 of the augmented matrix. Use an
appropriate multiple of row 1 and subtract it from row i to get a zero in the
(i,1) position in column 1 with
l A 1.
(ii). Move to column 2 and row 2 of the new version of the augmented
matrix. In the same way use row op erations to get zero in each (
l> 2) position
of column 2 with
l A 2.
(iii). Repeat this until all the components in the lower left part of the
subsequent augmented matrices are zero.
This is depicted in the Figure 2.2.1 where the (
l> m) component is about to be
set to zero.
Gaussian Elimination Algorithm.
define the augmented matrix [A d]
for j = 1,n-1 (forward sweep)
for i = j+1,n
add multiple of (row j) to (row i) to get
a zero in the (i,j) position
endloop
endloop
for i = n,1 (backward sweep)
solve for x
l
using row i
endloop.
The ab ove description is not very complete. In the forward sweep more de-
tails and special considerations with regard to roundo
errors are essential. The
© 2004 by Chapman & Hall/CRC
2.2. HEAT DIFFUSION AND GAUSS ELIMINATION 65
row operations in the inner loop may not be possible without some permutation
of the rows, for example,
D =
0 1
2 3
¸
=
More details about this can be found in Section 8.1. The backward sweep is
just the upper triangular solve step, and two versions of this were studied in the
previous section. The number of floating point operations needed to execute
the forward sweep is about equal to q
3
@3 where q is the number of unknowns.
So, if the number of unknowns doubles, then the number of operations will
increase by a factor of eight!
2.2.5 Implementation
MATLAB has a number of intrinsic procedures which are useful for illustration
of Gaussian elimination. These include lu, inv, A\d and others. The
OX
factorization of D can be used to solve D{ = g because D{ = (OX){ = O(X{) =
g= Therefore, first solve O| = g and second solve X{ = |. If both O and X are
known, then the solve steps are easy lower and upper triangular solves.
MATLAB and lu, inv and A\d
AA = [2 - 1 0;-1 2 -1;0 -1 2]
Ad = [62.5 62.5 62.5]’
Asol = A\d
sol =
93.7500
125.0000
93.750
A[L U] = lu(A)
L =
1.0000 0 0
-0.5000 1.0000 0
0 -0.6667 1.0000
U =
2.0000 -1.0000 0
0 1.5000 -1.0000
0 0 1.3333
AL*U
ans =
2 -1 0
-1 2 -1
0 -1 2
Ay = L\d
y =
© 2004 by Chapman & Hall/CRC
66 CHAPTER 2. STEADY STATE DISCRETE MODELS
62.5000
93.7500
125.0000
Ax =U\y
x =
93.7500
125.0000
93.7500
Ainv(A)
ans =
0.7500 0.5000 0.2500
0.5000 1.0000 0.5000
0.2500 0.5000 0.7500
Ainv(U)*inv(L)
ans =
0.7500 0.5000 0.2500
0.5000 1.0000 0.5000
0.2500 0.5000 0.7500
Computer codes for these calculations have been worked on for many decades.
Many of these codes are stored, updated and optimized for particular comput-
For example LU factorizations and
the upper triangular solves can be done by the LAPACK subroutines sgetrf()
The next M
ATLA B code, heatgelm.m, solves the 1D steady state heat diu-
sion problem for a number of di
erent values of q. Note that numerical solutions
converge to
x(lk) where x({) is the continuous model and k is the step size.
Lines 1-5 input the basic data of the model, and lines 6-16 define the right side,
g, and the coe!cient matrix, D. Line 17 converts the g to a column vector and
prints it, and line 18 prints the matrix. The solution is computed in line 19 and
printed.
MATLAB Code heatgelm.m
1. clear
2. n = 3
3. h = 1./(n+1);
4. K = .001;
5. beta = K/(h*h);
6. A= zeros(n,n);
7. for i=1:n
8. d(i) = sin(pi*i*h)/beta;
9. A(i,i) = 2;
10. if i
?n
11. A(i,i+1) = -1;
© 2004 by Chapman & Hall/CRC
ers in netlib (see http://www.netlib.org).
and sgetrs() and also sgesv(), see the user guide [1].
2.2. HEAT DIFFUSION AND GAUSS ELIMINATION 67
12. end;
13. if i
A1
14. A(i,i-1) = -1;
15. end;
16. end
17. d = d’
18. A
19. temp = A\d
Output for n = 3:
temp =
75.4442
106.6942
75.4442
Output for n = 7:
temp =
39.2761
72.5728
94.8209
102.6334
94.8209
72.5728
39.2761
2.2.6 Assessment
The above model for heat conduction depends upon the mesh size, k, but as the
mesh size
k goes to zero there will be little dierence in the computed solutions.
For example, in the MATLAB output, the component l of temp is the approxi-
mate temperature at
lk where k = 1@(q+1). The approximate temperatures at
the center of the wire are 106.6942 for
q = 3> 102=6334 for q = 7 and 101.6473 for
q = 15. The continuous model is (=001x
{
)
{
= vlq({) with x(0) = 0 = x(1),
and the solution is
x({) = (1000@
2
)vlq({)= So, x(1@2) = 1000@
2
= 101=3212,
which is approached by the numerical solutions as
q increases. An analysis of
this will be given in Section 2.6.
The four basic properties of inverse matrices need some justification.
Proof that the inverse is unique:
Let
E and F be inverses of D so that DE = ED = L and DF = FD = L.
Subtract these matrix equations and use the distributive property
DE DF = L L = 0
D(E F) = 0=
© 2004 by Chapman & Hall/CRC
