White R.E. Computational Mathematics: Models, Methods, and Analysis with MATLAB and MPI

Подождите немного. Документ загружается.

3.4. IDEAL FLUID FLOW 129

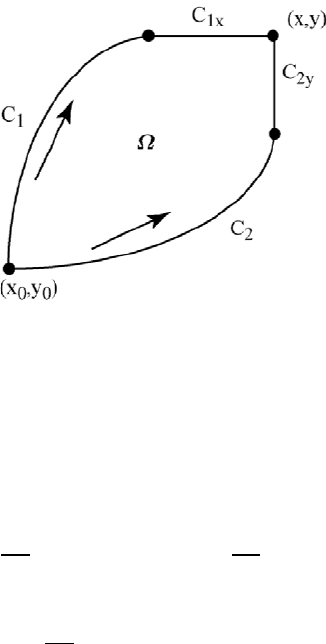
Figure 3.4.4: Two Paths to (x,y)

consider the special path

+ F

in Figure 3.4.4 and show 

{

= y = S



{

S g{ + Tg| +

S g{ + Tg|

= 0 +

S g{ + T0

The proof that 

= x = T is similar and uses the path F

+ F

in Figure

3.4.4. We have just proved the following theorem.

Theorem 3.4.1 (Existence of Stream Function) If u(x,y) and v(x,y) have con-

tinuous ﬁrst order partial derivatives and

{

+ y

= 0, then there is a stream

function such that (



{

> 

) = (y> x)=

3.4.7 Exercises

1. Consider the obstacle problem. Experiment with the dierent values of

z and hsv. Observe the number of iterations required for convergence.

2. Experiment with the mesh size and convince yourself the discrete problem

has converged to the continuous problem.

3. Experiment with the physical parameters

Z> O and incoming velocity x

4. Choose a di

erent s ize and shape obstacle. Compare the velocities near

the obstacle. What happens if there is more than one obstacle?

5. Prove the other part of Theorem 3.4.1



= x=

130 CHAPTER 3. POISSON EQUATION MODELS

3.5 Deformed Membrane and Steepest Descent

3.5.1 Introduction

The objective of this and the next section is to introduce the conjugate gradient

method for solving special algebraic systems where the coe

!cient matrix D is

symmetric (D = D

) and positive deﬁnite ({

D{ A 0 for all nonzero real vectors

{). Properties of these matrices also will be carefully studied in Section 8.2.

This method will be motivated by the applied problem to ﬁnd the deformation of

membrane if the position on the boundary and the pressure on the membrane

are known. The model will initially be in terms of ﬁnding the deformation

so that the potential energy of the membrane is a minimum, but it will be

reformulated as a partial di

erential equation. Also, the method of steepest

descent in a single direction will be introduced. In the next section this will be

generalized from the steepest descent method from one to multiple directions,

which will eventually give rise to the conjugate gradient method.

3.5.2 Applied Area

Consider a membrane whose edges are ﬁxed, for example, a musical drum. If

there is pressure (force per unit area) applied to the interior of the membrane,

then the membrane will deform. The objective is to ﬁnd the deformation for

every location on the membrane. Here we will only focus on the time indepen-

dent model, and also we will assume the deformation and its ﬁrst order partial

derivative are "relatively" small. These two assumptions will allow us to for-

mulate a model, which is similar to the heat di

usion and ﬂuid ﬂow models in

the previous sections.

3.5.3 Model

There will be three equivalent models. The formulation of the minimum po-

tential energy model will yield the weak formulation and the partial dierential

equation model of a steady state membrane with small deformation. Let

x({> |)

be the deformation at the space location (

{> |). The potential energy has two

parts: one from the expanded surface area, and one from an applied pressure.

Consider a small patch of the membrane above the rectangular region

{|.

The surface area above the region

{| is approximately, for a small patch,

V = (1 + x

{

+ x

)

1@2

{|=

The potential energy of this patch from the expansion of the membrane will be

prop ortional to the di

erence V  {|. Let the prop ortionality constant

be given by the tension

W . Then the potential energy of this patch from the

expansion is

W (V  {|) = W ((1 + x

{

+ x

)

1@2

 1){|=

3.5. DEFORMED MEMBRANE AND STEEPEST DESCENT 131

Now, apply the ﬁrst order Taylor polynomial approximation to

i(s) = (1 +

1@2

 i (0) + i

(0)(s  0)  1 + 1@2 s= Assume s = x

{

+ x

is small to get an

approximate potential energy

W (V  {|)  W@2 (x

{

+ x

){|= (3.5.1)

The potential energy from the applied pressure,

i({> |), is the force times

distance. Here force is pressure times area, i({> |){|= So, if the force is

positive when it is applied upward, then the potential energy from the applied

pressure is

xi{|= (3.5.2)

Combine (3.5.1) and (3.5.2) so that the approximate potential energy for the

patch is

W@2 (x

{

+ x

){|  xi{|= (3.5.3)

The potential energy for the entire membrane is found by adding the potential

energy for each patch in (3.5.3) and letting

{> | go to zero

potential energy =

S (x) 

(

W@2 (x

{

+ x

)  xi)g{g|= (3.5.4)

The choice of suitable

x({> |) should be a function such that this integral is ﬁnite

and the given deformations at the edge of the membrane are satisﬁed. Denote

this set of functions by

V. The precise nature of V is a little complicated, but

V should at least contain the continuous functions with piecewise continuous

partial derivatives so that the double integral in (3.5.4) exists.

Deﬁnition. The function

x in V is called an energy solution of the steady state

membrane problem if and only if

S (x) = plq

S (y) where y is any function in

V and S (x) is from (3.5.4).

The weak formulation is easily derived from the energy formulation. Let

* be any function that is zero on the boundary of the membrane and such

that

x + *, for 1 ?  ? 1, is also in the set of suitable functions, S. Deﬁne

I ()  S (x + *). If x is an energy solution, then I will be a minimum

real valued function at  = 0. Therefore, by expanding S (x + *), taking the

derivative with respect to

 and setting  = 0

0 = I

(0) = W

{

+ x

g{g| 

*ig{g|= (3.5.5)

Deﬁnition. The function

x in V is called a weak solution of the steady state

membrane problem if and only if (3.5.5) holds for all * that are zero on the

boundary and

x + * are in V.

We just showed an energy solution must also be a weak solution. If there

is a weak solution, then we can show there is only one such solution. Suppose

132 CHAPTER 3. POISSON EQUATION MODELS

x and X are two weak solutions so that (3.5.5) must hold for both x and X.

Subtract these two versions of (3.5.5) to get

0 =

{

+ x

g{g|  W

{

+ X

g{g|

= W

(

x  X)

{

+ (x  X)

g{g|= (3.5.6)

Now, let

z = x  X and note it is equal to zero on the boundary so that we

may choose

* = z= Equation (3.5.6) becomes

0 =

{

+ z

g{g|=

Then both partial derivatives of z must be zero so that z is a constant. But,

z is zero on the boundary and so z must be zero giving x and X are equal.

A third formulation is the partial di

erential equation model. This is often

called the classical model and requires second order partial derivatives of

The ﬁrst two models only require ﬁrst order partial derivatives.

W (x

{{

+ x

) = i= (3.5.7)

Deﬁnition. The classical solution of the steady state membrane problem re-

quires u to satisfy (3.5.7) and the given values on the boundary.

Any classical solution mu st be a weak solution. This follows from the con-

clusion of Green’s theorem

{

 S

g{g| =

S g{ + Tg|=

Let T = W *x

{

and S = W*x

and use * = 0 on the boundary so that the

line integral on the right side is zero. The left side is

(

W *x

{

)

{

 (W *x

)

g{g| =

W *

{

+ W *

+ W (x

{{

+ x

)*g{g|=

Because x is a classical solution and the right side is zero, the conclusion of

Greens’s theorem gives

W *

{

+ W *

 *ig{g| = 0=

This is equivalent to (3.5.5) so that the classical solution must be a weak solu-

tion.

We have shown any energy or classical solution must be a weak solution.

Since a weak solution must be unique, any energy or classical s olution must

be unique. In fact, the three formulations are equivalent under appropriate

assumptions. In order to understand this, one must be more careful about the

deﬁnition of a suitable set of functions,

V. However, we do state this result

even though this set has not been precisely deﬁned. Note the energy and weak

solutions do not directly require the existence of second order derivatives.

3.5. DEFORMED MEMBRANE AND STEEPEST DESCENT 133

Theorem 3.5.1 (Equivalence of Formulations) The energy, weak and classical

formulations of the steady state membrane are equivalent.

3.5.4 Method

The energy formulation can be discretized via the classical Rayleigh-Ritz ap-

proximation scheme where the solution is approximated by a linear combination

of a ﬁnite number of suitable functions,

({> |), where m = 1> · · · > q

({> |) 

m=1

({> |)= (3.5.8)

These functions could be p olynomials, trig functions or other likely candidates.

The coe!cients, x

, in the linear combination are the unknowns and must be

chosen so that the energy in (3.5.4) is a minimum

I (x

> · · · > x

)  S (

m=1

({> |))= (3.5.9)

Deﬁnition. The Rayleigh-Ritz approximation of the energy formulation is

given by u in (3.5.8) where

are chosen such that I : R

$ R in (3.5.9) is a

minimum.

The

can be found from solving the algebraic system that comes from

setting all the ﬁrst order partial derivatives of

I equal to zero.

0 =

m=1

+ *

g{g|)x



ig{g|

m=1

 g

= the l component of Dx  g where (3.5.10)

 W

+ *

g{g| and



ig{g|=

This algebraic system can also be found from the weak formulation by putting

x({> |) in (3.5.8) and * = *

({> |) into the weak equation (3.5.5). The matrix

D has the following properties: (i) symmetric, (ii) positive deﬁnite and (iii)

I (x) = 1@2 x

Dx  x

g= The s ymmetric property follows from the deﬁnition

of d

. The positive deﬁnite property follows from

@2 x

Dx = W@2

(

m=1

)

+ (

m=1

)

g{g| A 0= (3.5.11)

134 CHAPTER 3. POISSON EQUATION MODELS

The third property follows from the deﬁnitions of

I> D and g. The following

important theorem shows that the algebraic problem

Dx = g (3.5.10) is equiv-

alent to the minimization problem given in (3.5.9). A partial proof is given at

the end of this section, and this important result will be again used in the next

Theorem 3.5.2 (Discrete Equivalence Formulations) Let A be any symmetric

positive deﬁnite matrix. The following are equivalent: (i) D{ = g and (ii) M({)

= plq

M(|) where M({) 

{

D{  {

The steepest descent method is based on minimizing the discrete energy

integral, which we will now denote by

M({). Suppose we make an initial guess,

{, for the solution and desire to move in some direction s so that the new

{, {

= { + fs, will make M({

) a minimum. The direction, s, of steepest

descent, where the directional derivative of

M({) is largest, is given by s =

uM({)  [M({)

{

] = (g  D{)  u. Once this direction has been established

we need to choose the

f so that i(f) = M({ + fu) is a minimum where

M({ + fu) =

(

{ + fu)

D({ + fu)  ({ + fu)

Because D is symmetric, u

D{ = {

Du and

M({ + fu) =

{

D{ + fu

D{ +

Du  {

g  fu

= M({)  fu

(g  D{) +

= M({)  fu

u +

Du=

Choose f so that fu

u +

Du is a minimum. You can use derivatives or

complete the square or you can use the d iscrete equivalence theorem. In the

latter case

{ is replaced by f and the matrix D is replaced by the 1 × 1 matrix

Du> which is positive for nonzero u because D is positive deﬁnite. Therefore,

f = u

u@u

Du.

Steepest Descent Method for

M({) = plq

M(|)=

Let {

be an initial guess

= g  D{

for m = 0, maxm

f = (u

)

@(u

)

{

p+1

= {

+ fu

p+1

= u

 fDu

test for convergence

endloop.

section and in Chapter9.

3.5. DEFORMED MEMBRANE AND STEEPEST DESCENT 135

In the above the next residual is computed in terms of the previous residual

p+1

= u

 fDu

. This is valid because

p+1

= g  D({

+ fu

) = g  D{

 D(fu

) = u

 fDu

The test for convergence could be the norm of the new residual or the norm of

the residual relative to the norm of g.

3.5.5 Implementation

MATLAB will be used to execute the steep est descent method as it i s applied to

the ﬁnite dierence model for x

{{

 x

= i= The coe!cient matrix is positive

deﬁnite, and so, we can use this particular scheme. In the M

ATLA B code st.m

the partial di

erential equation has right side equal to 200(1+vlq({)vlq(|)),

and the solution is required to b e zero on the boundary of (0> 1) × (0> 1). The

right side is computed and stored in lines 13-18. The vectors are represented

as 2D arrays, and the sparse matrix

D is not explicitly stored. Observe the use

of array operations in lines 26, 32 and 35. The while loop is executed in lines

23-37. The matrix product Du is stored in the 2D array t and is computed in

lines 27-31 where we have used u is zero on the boundary nodes. The value for

f = u

u@u

Du is alpha as computed in line 32. The output is given in lines 38

and 39 where the semilog plot for the norm of the error versus the iterations is

generated by the MATLAB command semilogy(reserr).

MATLAB Code st.m

1. clear;

2. %

3. % Solves -uxx -uyy = 200+200sin(pi x)sin(pi y)

4. % Uses u = 0 on the boundary

5. % Uses steepest descent

6. % Uses 2D arrays for the column vectors

7. % Does not explicitly store the matrix

8. %

9. n = 20;

10. h = 1./n;

11. u(1:n+1,1:n+1)= 0.0;

12. r(1:n+1,1:n+1)= 0.0;

13. r(2:n,2:n)= 1000.*h*h;

14. for j= 2:n

15. for i = 2:n

16. r(i,j)= h*h*200*(1+sin(pi*(i-1)*h)*sin(pi*(j-1)*h));

17. end

18. end

19. q(1:n+1,1:n+1)= 0.0;

20. err = 1.0;

21. m = 0;

136 CHAPTER 3. POISSON EQUATION MODELS

22. rho = 0.0;

23. while ((errA.0001)*(m?200))

24. m = m+1;

25. oldrho = rho;

26. rho = sum(sum(r(2:n,2:n).^2)); % dotproduct

27. for j= 2:n % sparse matrix product Ar

28. for i = 2:n

29. q(i,j)=4.*r(i,j)-r(i-1,j)-r(i,j-1)-r(i+1,j)-r(i,j+1);

30. end

31. end

32. alpha = rho/sum(sum(r.*q)); % dotproduct

33. u = u + alpha*r;

34. r = r - alpha*q;

35. err = max(max(abs(r(2:n,2:n)))); % norm(r)

36. reserr(m) = err;

37. end

38. m

39. semilogy(reserr)

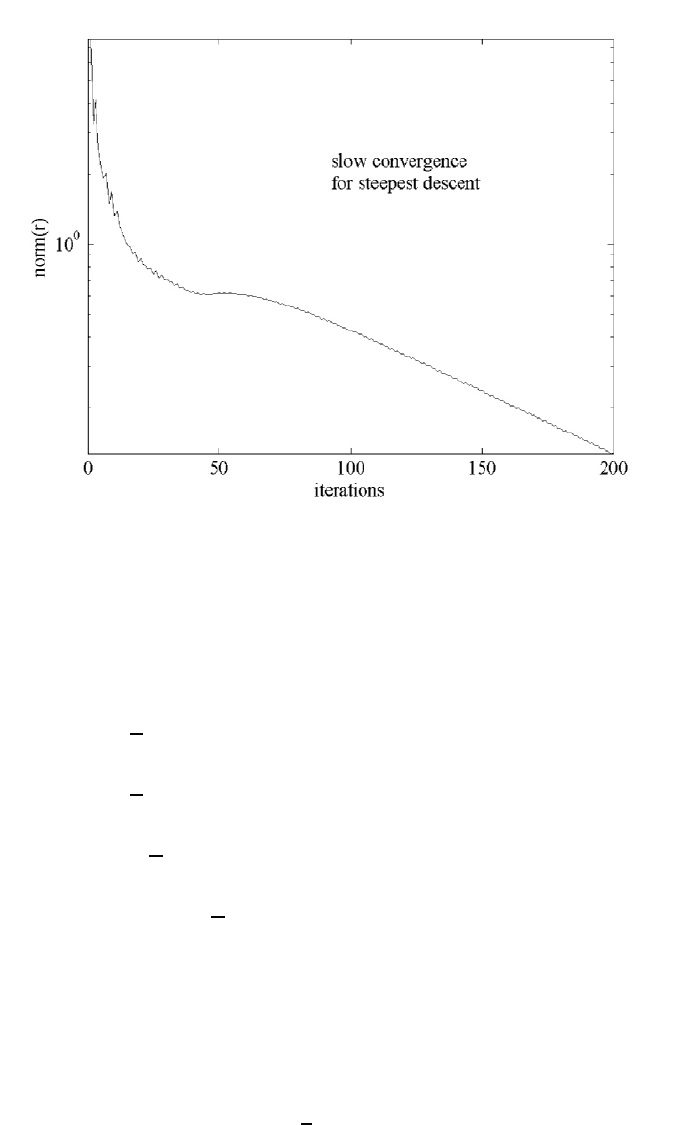
The steepest descent method appears to be converging, but after 200 iter-

ations the norm of the residual is still only about .01. In the next section the

conjugate gradient method will be described. A calculation with the conjugate

gradient method shows that after only 26 iterations, the norm of the residual

is ab out .0001. Generally, the steepest descent method is slow relative to the

conjugate gradient method. This is because the minimization is only in one

direction and not over higher dimensional sets.

3.5.6 Assessment

The Rayleigh-Ritz and steepest descent methods are classical methods, which

serve as introductions to current numerical methods such as the ﬁnite element

discretization method and the conjugate gradient iterative methods. M

ATLAB

has a very nice partial dierential equation toolbox that implements some of

these. For more information on various conjugate gradient schemes use the

ATLAB help command for pcg (preconditioned conjugate gradient).

The proof of the discrete equivalence theorem is based on the following

matrix calculations. First, we will show if

D is symmetric positive deﬁnite and

{ satisﬁes D{ = g, then M({)  M(|) for all |. Let | = { + (|  {) and use

3.5. DEFORMED MEMBRANE AND STEEPEST DESCENT 137

Figure 3.5.1: Steepest Descent norm(r)

D = D

and u = g  D{ = 0

M(|) =

(

{ + (|  {))

D({ + (|  {))  ({ + (|  {))

{

D{ + (|  {)

(

|  {)

D(|  {)  {

g  (|  {)

= M({) +

(

|  {)

D(|  {)= (3.5.12)

Because

D is positive deﬁnite, (|  {)

D(|  {) is greater than or equal to zero.

Thus,

M(|) is greater than or equal to M({).

Second, we show if

M({) = plq

M(|),then u = u({) = 0= Suppose u is not

the zero vector so that

u A 0 and u

Du A 0= Cho ose | so that |  { = uf

and 0  M(|)  M({) = fu

u +

Du. Let f = u

u@u

Du to give a

contradiction for small enough

=

The weak formulation was used to show that any solution must be unique. It

also can be used to formulate the ﬁnite element method, which is an alternative

to the ﬁnite dierence method. The ﬁnite dierence method requires the domain

to be a union of rectangles. One version of the ﬁnite element method uses

the space domain as a ﬁnite union of triangles (elements) and the

({> |) are

piecewise linear functions on the triangles. For node

m let *

({> |) be continuous,

equal to 1.0 at node

m, be a linear function for ({> |) in an adjacent triangles,

138 CHAPTER 3. POISSON EQUATION MODELS

and zero elsewhere. This allows for the numerical approximations on domains

that are not rectangular. The interested reader should see the M

ATLAB code

3.5.7 Exercises

1. Verify line (3.5.5).

2. Verify lines (3.5.10) and (3.5.11).

3. Why is the steepest descent direction equal to

uM? Show uM = u> that

is, M({)

{

= (g  D{)

{

4. Show the formula for the f = u

u@u

Du in the steepest descent method

is correct via both derivative and completing the square.

5. Duplicate the M

AT LAB Experiment

with the error tolerance

huu = 2=0> 1=0> 0=5 and 0.1.

6. In the M

AT LAB code st.m change the right side to 100{| + 40{

7. In the M

ATLA B code st.m change the boundary conditions to x({> 1) =

{(1  {) and zero elsewhere. Be careful in the matrix product t = Du!

8. Fill in all the details leading to (3.5.12).

3.6 Conjugate Gradient Method

3.6.1 Introduction

The conjugate gradient method has three basic components: steep est descent

in multiple directions, conjugate directions and preconditioning. The multiple

direction version of steepest descent insures the largest possible decrease in the

energy. The conjugate direction insures that solution of the reduced algebraic

system is done with a minimum amount of computations. The preconditioning

mo diﬁes the initial problem so that the convergence is more rapid.

3.6.2 Method

The steepest d escent method hinges on the fact that for symmetric positive

deﬁnite matrices the algebraic system

D{ = g is equivalent to minimizing a

real valued function

M({) =

{

D{  {

g, which for the membrane problem

is a discrete approximation of the potential energy of the membrane. Make an

initial guess,

{, for the solution and move in some direction s so that the new {,

{

= {+fs, will make M({

) a minimum. The direction, s, of steepest descent,

where the directional derivative of

M is largest, is given by s = u. Next choose

the

f so that I (f) = M({ + fu) is a minimum, and this is f = u

u@u

Du.

In the steep est descent method only the current residual is used. If a linear

combination of all the previous residuals were to be used, then the "energy",

M(b{

), would be smaller than the M({

) for the steepest descent method.

computations giving Figure 3.5.1.

fem2d.m and R. E. White [27].