White R.E. Computational Mathematics: Models, Methods, and Analysis with MATLAB and MPI
Подождите немного. Документ загружается.

3.2. HEAT TRANSFER IN 2D FIN AND SOR 109
3.2.3 Model
The partial dierential equation (3.2.2) is usually associated with boundary
conditions, which may or may not have derivatives of the solution. For the
present, we will assume the temperature is zero on the boundary of (0> O) ×
(0
> Z )> O = Z = 1> N = 1> i ({> |) = 0 and W = 2. So, equation (3.2.2)
simplifies to
x
{{
x
||
+ fx = fx
vxu
= (3.2.3)
Let
x
l>m
be the approximation of x(lk> mk) where k = g{ = g| = 1=0@q.
Approximate the s econd order partial derivatives by the centered finite dif-
ferences, or use (3.2.1) with similar approximations to Nx
|
({> | + |@2)
N
(x
l>m+1
x
lm
)@k.
Finite Di
erence Model of (3.2.3).
[(x
l+1
>
m
x
l>m
)@k (x
l>m
x
l1>m
)@k]@k
[(x
l>m+1
x
l>m
)@k (x
l>m
x
l>m1
)@k]@k
+fx
l>m
= fx
vxu
where 1 l> m q 1= (3.2.4)
There are (
q 1)
2
equations for (q 1)
2
unknowns x
l>m
. One can write
equation (3.2.4) as fixed point equations by multiplying both sides by
k
2
, letting
i = fx
vxu
and solving for x
l>m
x
l>m
= (k
2
i
lm
+ x
l>m1
+ x
l1>m
+ x
l+1>m
+ x
l>m+1
)@(4 + fk
2
)= (3.2.5)
3.2.4 Method
The point version of SOR for the problem in (3.2.4) or (3.2.5) can be very
e
!ciently implemented because we know exactly where and what the nonzero
components are in each row of the coe
!cient matrix. Since the unknowns are
identified by a grid pair (
l> m), the SOR computation for each unknown will be
done within two nested loops. The classical order is given by having the i-loop
inside and the j-loop on the outside. In this application of the SOR algorithm
the lower sum is
x(l> m1)+x(l1> m) and the upper sum is x(l+1> m)+x(l> m+1)=
SOR Algorithm for (3.2.5) with f = cu
vxu
=
for m = 0, maxit
for j = 2, n
for i = 2,n
utemp=(h*h*f(i,j) + u(i,j-1) + u(i-1,j)
+ u(i+1,j ) + u(i,j+1))/(4+c*h*h)
u(i,j)=(1-
$)*u(i,j)+$*utemp
endloop
endloop
test for convergence
endloop.
© 2004 by Chapman & Hall/CRC
110 CHAPTER 3. POISSON EQUATION MODELS
The fi nite di
erence model in (3.2.5) can be put into matrix form by mul-
tiplying the equations (3.2.5) by
k
2
and listing the unknowns starting with
the smallest | values (smallest m) and moving from the smallest to the largest
{ values (largest l). The first grid row of unknowns is denoted by X
1
=
[
x
11
x
21
x
31
x
41
]
W
for q = 5. Hence, the block form of the above system
with boundary values set equal to zero is
5
9
9
7
E L
L E L
L E L
L E
6
:
:
8
5
9
9
7
X
1
X
2
X
3
X
4
6
:
:
8
= k
2
5
9
9
7
I
1
I
2
I
3
I
4
6
:
:
8
where
E =
5
9
9
7
4 + k
2
f 1
1 4 + k
2
f 1
1 4 + k
2
f 1
1 4 + k
2
f
6
:
:
8
>
X
m
=
5
9
9
7
x
1m
x
2m
x
3m
x
4m
6
:
:
8
> I
m
=
5
9
9
7
i
1m
i
2m
i
3m
i
4m
6
:
:
8
with i
lm
= i(lk> mk)=
The above block tridiagonal system is a special case of the following block
tridiagonal system where all block components are
Q × Q matrices (Q = 4).
The block system has Q
2
blocks, and so there are Q
2
unknowns. If the full
version of the Gaussian elimination algorithm was used, it would require ap-
proximately (
Q
2
)
3
@3 = Q
6
@3 operations
5
9
9
7
D
1
F
1
E
2
D
2
F
2
E
3
D
3
F
3
E
4
D
4
6
:
:
8
5
9
9
7
[
1
[
2
[
3
[
4
6
:
:
8
=
5
9
9
7
G
1
G
2
G
3
G
4
6
:
:
8
=
Or, for [
0
= 0 = [
5
and l = 1> 2> 3> 4
E
l
[
l1
+ D
l
[
l
+ F
l
[
l+1
= G
l
= (3.2.6)
In the block tridiagonal algorithm for (3.2.6) the entries are either Q × Q
matrices or Q × 1 column vectors. The "divisions" for the "point" tridiagonal
algorithm must be replaced by matrix solves, and one must be careful to pre-
serve the proper order of matrix multiplication. The derivation of the following
is similar to the derivation of the point form.
Block Tridiagonal Algorithm for (3.2.6).
(1) = A(1), solve (1)*g(1)= C(1) and solve (1)*Y(1) = D(1)
for i = 2, N
(i) = A(i)- B(i)*g(i-1)
© 2004 by Chapman & Hall/CRC
3.2. HEAT TRANSFER IN 2D FIN AND SOR 111
solve
(i)*g(i) = C(i)
solve
(i)*Y(i) = D(i) - B(i)*Y(i-1)
endloop
X(N) = Y(N)
for i = N - 1,1
X(i) = Y(i) - g(i)*X(i+1)
endloop.
The block or line version of the SOR algorithm also requires a matrix solve
step in place of a "division." Note the matrix solve has a point tridiagonal
matrix for the problem in (3.2.4).
Block SOR Algorithm for (3.2.6).
for m = 1,maxit
for i = 1,N
solve A(i)*Xtemp = D(i) - B(i)*X(i-1) - C(i)*X(i+1)
X(i) = (1-w)*X(i) + w*Xtemp
endloop
test for convergence
endloop.
3.2.5 Implementation
The point SOR algorithm for a cooling plate, which has a fixed temperature at
its boundary, is relatively easy to code. In the MATLAB function file sor2d.m,
there are two input parameters for
q and z, and there are outputs for z, vrulwhu
(the number of iterations needed to "converge") and the array x (approximate
temperature array). The boundary temperatures are fixed at 200 and 70 as
given by lines 7-10 where
rqhv(q + 1) is an (q + 1) × (q + 1) array whose
components are all equal to 1, and the values of
x in the interior nodes define
the initial guess for the S OR method. The surrounding temperature is defined
in line 6 to be 70, and so the steady state temperatures should be between 70
and 200. Lines 14-30 contain the SOR loops. The unknowns for the interior
nodes are approximated in the nested loops beginning in lines 17 and 18. The
counter
qxpl indicates the number of nodes that satisfy the error tolerance,
and
qxpl is initialized in line 15 and updated in lines 22-24. If qxpl equals the
number of unknowns, then the SOR loop is exited, and this is tested in lines
27-29. The outputs are given in lines 31-33 where phvkf({> |> x0) generates a
surface and contour plot of the approximated temperature. A similar code is
sor2d.f90 written in Fortran 9x.
MATLAB Code sor2d.m
1. function [w,soriter,u] = sor2d(n,w)
2. h = 1./n;
3. tol =.1*h*h;
© 2004 by Chapman & Hall/CRC
112 CHAPTER 3. POISSON EQUATION MODELS
4. maxit = 500;
5. c = 10.;
6. usur = 70.;
7. u = 200.*ones(n+1); % initial guess and hot boundary
8. u(n+1,:) = 70; % cooler boundaries
9. u(:,1) = 70;
10. u(:,n+1) = 70
11. f = h*h*c*usur*ones(n+1);
12. x =h*(0:1:n);
13. y = x;
14. for iter =1:maxit % begin SOR iterations
15. numi = 0;
16. for j = 2:n % loop over all unknowns
17. for i = 2:n
18. utemp = (f(i,j) + u(i,j-1) + u(i-1,j) +
u(i+1,j) + u(i,j+1))/(4.+h*h*c);
19. utemp = (1. - w)*u(i,j) + w*utemp;
20. error = abs(utemp - u(i,j));
21. u(i,j) = utemp;
22. if error
?tol % test each node for convergence
23. numi = numi + 1;
24. end
25. end
26. end
27. if numi==(n-1)*(n-1) % global convergence test
28. break;
29. end
30. end
31. w
32. soriter = iter
33. meshc(x,y,u’)
f = 10=0, and one can see the
plate has been cooled to a lower temperature. Also, we have graphed the
temperature by indicating the equal temperature curves or contours. For 39
2
unknowns, error tolerance wro = 0=01k
2
and the SOR parameter $ = 1=85, it
other choices of
$> and this indicates that $ near 1.85 gives convergence in a
minimum number of SOR iterations.
3.2.6 Assessment
In the first 2D heat diusion model we kept the boundary conditions simple.
However, in the 2D model of the cooling fin one should consider the heat that
passes through the edge portion of the fin. This is similar to what was done
for the cooling fin with di
usion in only the { direction. There the heat flux
© 2004 by Chapman & Hall/CRC
took 121 iterations to converge. Table 3.2.1 records numerical experiments with
The graphical output in Figure 3.2.2 is for
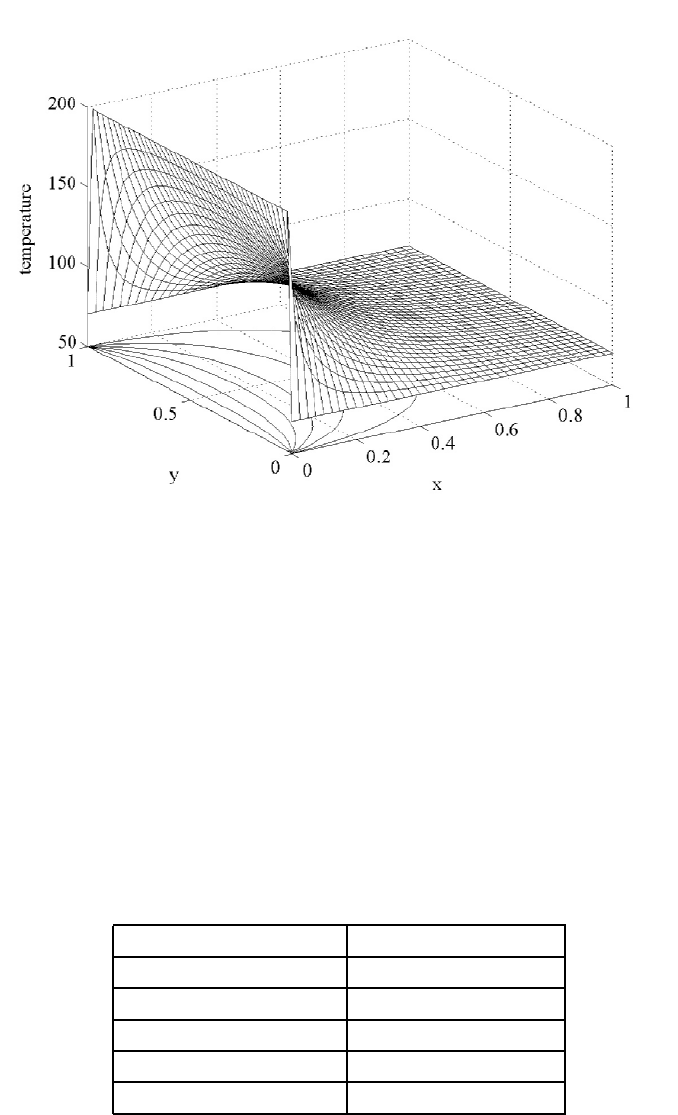
3.2. HEAT TRANSFER IN 2D FIN AND SOR 113
Figure 3.2.2: Temperature and Contours of Fin
Table 3.2.1: Convergence and SOR Parameter
SOR Parameter Iter. for Conv.
1.60 367
1.70 259
1.80 149
1.85 121
1.90 167
© 2004 by Chapman & Hall/CRC
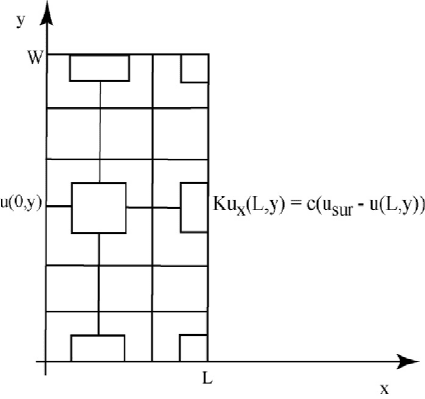
114 CHAPTER 3. POISSON EQUATION MODELS
Figure 3.2.3: Cooling Fin Grid
at the tip was given by the boundary condition
Nx
{
(O) = f(x
vxu
x(O)). For
the 2D steady state cooling fin model we have similar boundary conditions on
the edge of the fin that is away from the mass to be cooled.
The fi nite di
erence model must have additional equations for the cells near
the edge of the fin. So, in Figure 3.2.3 there are 10 equations for the (
{
|
) cells (interior), 5 equations for the ({@2 |) cells (right), 4 equations for
the (
{ |@2) cells (bottom and top) and 2 equations for the ({@2 |@2)
cells (corner). For example, the cells at the rightmost side with ({@2 |) the
finite dierence equations are for l = q{ and 1 ? m ? q|. The other portions
of the boundary are similar, and for all the details the reader should examine
the Fortran code fin2d.f90.
Finite Dierence Model of (3.2.2) where i = nx and 1 ? j ? ny.
0 = (2{@2 |)f(x
vxu
x
q{>m
)
+(
{@2 W )[N(x
q{>m+1
x
q{>m
)@| N(x
q{>m
x
q{>m1
)@|]
+(
|W )[f(x
vxu
x
q{>m
) N(x
q{>m
x
q{1>m
)@{]= (3.2.7)
Another question is related to the existence of solutions. Note the diagonal
components of the coe
!cient matrix are much larger than the o diagonal
components. For each row the diagonal component is strictly larger than the
sum of the absolute value of the o diagonal components. In the finite dierence
model for (3.2.4) the diagonal component is 4
@k
2
+ f and the four o diagonal
components are
1@k
2
. So, like the 1D cooling fin model the 2D cooling fin
model has a strictly diagonally dominant coe
!cient matrix.
© 2004 by Chapman & Hall/CRC

3.2. HEAT TRANSFER IN 2D FIN AND SOR 115
Theorem 3.2.1 (Existence Theorem) Consider
D{ = g and assume D is
strictly diagonally dominant. If there is a solution, it is unique. Moreover,
there is a solution.
Proof. Let
{ and | be two solutions. Then D({ |) = 0. If { | is not a
zero column vector, then we can choose
l so that |{
l
|
l
| = pd{
m
|{
m
|
m
| A 0=
d
ll
({
l
|
l
) +
X
m6=l
d
lm
({
m
|
m
) = 0=
Divide by {
l
|
l
and use the triangle inequality to contradict the strict di-
agonal dominance. Since the matrix is square, the existence follows from the
uniqueness.
3.2.7 Exercises
1. Consider the MATLA B code for the point SOR algorithm.
(b). Experiment with the convergence parameter
wro and observe the number
of iterations required for convergence.
2. Consider the M
AT LAB code for the point SOR algorithm. Experiment
with the SOR parameter
$ and observe the number of iterations for convergence.
Do this for q = 5> 10> 20 and 40 and find the $ that gives the smallest number
of iterations for convergence.
3. Consider the M
ATLA B code for the point SOR algorithm. Let f = 0>
i
({> |) = 2
2
vlq({)vlq(|) and require x to be zero on the boundary of
(0
> 1) × (0> 1).
(a). Show the solution is x({> |) = vlq({)vlq(|).
(b). Compare it with the numerical solution with
q = 5> 10> 20 and 40.
Observe the error is of order k
2
.
(c). Why have we used a convergence test with wro = hsv k k?
4. In the M
ATLA B code modify the boundary conditions so that at x(0> |) =
200,
x({> 0) = x({> 1) = x(1> |) = 70= Experiment with q and $=
5. Implement the block tridiagonal algorithm for problem 3.
6. Implement the block SOR algorithm for problem 3.
7. Use Theorem 3.2.1 to show the block diagonal matrix from (3.2.4) for
the block SOR is nonsingular.
8. Use the Schur complement as in Section 2.4 and Theorem 3.2.1 to show
the alpha matrices in the block tridiagonal algorithm applied to (3.2.4) are
nonsingular.
© 2004 by Chapman & Hall/CRC
(a). Verify the calculations in Table 3.2.1.
116 CHAPTER 3. POISSON EQUATION MODELS
3.3 Fluid Flow in a 2D Porous Medium
3.3.1 Introduction
In this and the next section we present two fluid fl ow models in 2D: flow in a
porous media and ideal fluids. Both these models are similar to steady state
2D heat di
usion. The porous media flow uses an empirical law called Darcy’s
law, which is similar to Fourier’s heat law. An application of this model to
groundwater management will be studied.
3.3.2 Applied Area
In both applications assume the velocity of the fluid is (x({> |)> y({> |)> 0), that
is, it is a 2D steady state fluid flow. In flows for both a porous medium and ideal
fluid it is useful to be able to give a mathematical description of compressibility
of the fluid. The compressibility of the fluid can be quantified by the divergence
of the velocity. In 2D the divergence of (u,v) is
x
{
+ y
|
. This indicates how
much mass enters a small volume in a given unit of time. In order to understand
density
and approximate x
{
+ y
|
by finite dierences. Let w be the change
in time so that
x({ + {> |)w approximates the change in the { direction of
the mass leaving (for
x({ + {> |) A 0) the front face of the volume ({|W ).
change i n mass = sum via four vertical faces of (
{|W )
=
W | (x({ + {> |) x({> |))w
+W { (y({> | + |) y({> |))w= (3.3.1)
Divide by (
{|W )w and let { and | go to zero to get
rate of change of mass per unit volume =
(x
{
+ y
|
)= (3.3.2)
If the fluid is incompressible, then
x
{
+ y
|
= 0.
Consider a shallow saturated porous medium with at least one well. Assume
the region is in the xy-plane and that the water moves towards the well in such
a way that the velocity vector is in the xy-plane. At the top and bottom of the
xy region assume there is no flow through these boundaries. However, assume
there is ample supply from the left and right boundaries so that the pressure is
fixed. The problem is to determine the flow rates of well(s), location of well(s)
and number of wells so that there is still water to be pumped out. If a cell does
not contain a well and is in the interior, then
x
{
+ y
|
= 0= If there is a well in
a cell, then x
{
+ y
|
? 0=
3.3.3 Model
Both porous and ideal flow models have a partial dierential equation similar
to that of the 2D heat di
usion model, but all three have dierent boundary
© 2004 by Chapman & Hall/CRC
this, consider the small thin rectangular mass as depicted in Figure 3.3.1 with
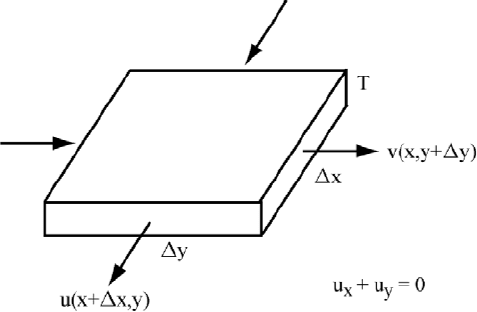
3.3. FLUID FLOW IN A 2D POROUS MEDIUM 117
Figure 3.3.1: Incompressible 2D Fluid
conditions. For porous fluid flow problems, boundary conditions are either a
given function along part of the boundary, or a zero derivative for the other
parts of the boundary. The motion of the fluid is governed by an empirical law
called Darcy’s law.
Darcy Law.
(
x> y) = N(k
{
> k
|
) where (3.3.3)
k is the hydraulic head pressure and
N is the hydraulic conductivity.
The hydraulic conductivity depends on the pressure. However, if the porous
medium is saturated, then it can be assumed to be constant. Next couple
Darcy’s law with the divergence of the velocity to get the following partial
di
erential equation for the pressure.
x
{
+ y
|
= (Nk
{
)
{
(Nk
|
)
|
= i= (3.3.4)
Groundwater Fluid Flow Model.
(Nk
{
)
{
(Nk
|
)
|
=
½
0 > ({> |) @5 zhoo
U >
({> |) 5 zhoo
({> |) 5 (0> O) × (0> Z )>
Nk
|
= 0 for | = 0 and | = Z and
k = k
4
for { = 0 and { = O=
3.3.4 Method
We will use the finite dierence method coupled with the SOR iterative scheme.
For the (
{|) cells in the interior this is similar to the 2D heat diusion
problem. For the portions of the boundary where a derivative is set equal to
© 2004 by Chapman & Hall/CRC

118 CHAPTER 3. POISSON EQUATION MODELS
Figure 3.3.2: Groundwater 2D Porous Flow
zero on a half cell (
{@2 |) or ({ |@2) as in Figure 3.3.2, we insert some
additional code inside the SOR loop. For example, consider the groundwater
model where k
|
= 0 at | = Z on the half cell ({ |@2). The finite dierence
equations for
x = k , g{ = { and g| = | in (3.3.5) and corresponding line
of SOR code in (3.3.6) are
0 =
[(0) (x(l> m) x(l> m 1))@g|]@(g|@2)
[(x(l + 1> m) x(l> m))@g{
(x(l> m) x(l 1> m))@g{]@g{ (3.3.5)
xwhps = ((x(l + 1> m) + x(l 1> m))@(g{ g{)
+2
x(l> m 1)@(g| g|))@(2@(g{ g{) + 2@(g| g|))
x(l> m) = (1 z) x(l> m) + z xwhps= (3.3.6)
3.3.5 Implementation
In the following MATL AB code p or2d.m the SOR method is used to solve the
discrete model for steady state saturated 2D groundwater porous flow. Lines
1-44 initialize the data. It is interesting to experiment with
hsv in line 6, the
SOR parameter zz in line 7, q{ and q| in lines 9,10, the location and flow
rates of the wells given in lines 12-16, and the size of the flow field given in
lines 28,29. In line 37 R_well is calibrated to be independent of the mesh.
The SOR iteration is done in the while loop in lines 51-99. The bottom nodes
in lines 73-85 and top nodes in lines 86-97, where there are no flow boundary
conditions, must b e treated di
erently from the interior nodes in l ines 53-71.
The locations of the two wells are given by the if statements in lines 58-63.
The output is in lines 101-103 where the number of iterations for convergence
and the SOR parameter are printed, and the surface and contour plots of the
pressure are graphed by the M
ATLAB command meshc(x,y,u’). A similar code
is por2d.f90 written in Fortran 9x.
© 2004 by Chapman & Hall/CRC
