Weinan E. Principles of Multiscale Modeling
Подождите немного. Документ загружается.


2.6. RENORMALIZATION GROUP ANALYSIS 77
Figure 2.6: Typical spin configurations for the two-dimensional Ising model at low, critical
and high temperatures (produced by Hao Shen).

78 CHAPTER 2. ANALYTICAL METHODS
3. ν can be found via linearizing R at its fixed point. For |K − K
∗
| ≪ 1,
K
L
= R(K) = K
∗
+ λ(K − K
∗
) + ···
where λ =
dR
dK
(K
∗
), therefore
1
L
=
ξ(K
L
)
ξ(K)
=
|T
L
− T
∗
|
−ν
|T − T
∗
|
−ν
=
|K
∗
− K
L
|
−ν
|K
∗
− K|
−ν
= λ
−ν
This gives a prediction on the value of ν.
2.6.2 An illustration of the renormalization transformation
It is useful to first illustrate the basic ideas of renormalization group analysis using
the one-dimensional Ising model. Consider a one-dimensional lattice with N sites. At
the jth site, we assign a spin variable s
j
, which takes two possible values +1, −1. The
Hamiltonian of this model is given by
H = −J
X
|i−j|=1
s
i
s
j
. (2.6.5)
J > 0 so that neighboring spins tend to align with each other to lower the value of the
Hamiltonian.
Renormalization group analysis proceeds as follows. First, let us define a coarse-
graining operator, the renormalization group flow. For example, starting with a system
with N sites (N is assumed to be even), we integrate out the spin variables on the even
sites and take only the odd ones {s
1
, s
3
, . . . , s
N−1
} as the variables of our system.
Next we define the renormalization group flow. The transformation
{s
1
, s
2
, . . . , s
N
} → {s
1
, s
3
, . . . , s
N−1
}
induces a transformation in the space of the models (the Hamiltonians). After summing
over s
2
, s
4
, etc, the partition function becomes
Z(N, K) =
X
{s
j
}
exp(K(s
1
s
2
+ s
2
s
3
+ . . .))
=
X
s
1
s
3
...
(exp(K(s
1
+ s
3
)) + exp(−K(s
1
+ s
3
)))
× (exp(K(s
3
+ s
5
)) + exp(−K(s
3
+ s
5
))) ···

2.6. RENORMALIZATION GROUP ANALYSIS 79
We view this new form of the partition function as the partition function of a new
Hamiltonian on a lattice with N/2 sites. This means that we would like to find a constant
K
L
(L = 2) such that
Z(N, K) =
X
s
1
s
3
...
exp(K
L
(s
1
s
3
+ s
3
s
5
+ . . .))f(K)
N/2
. (2.6.6)
Here the last term is a scaling factor that has to be introduced to compensate for the
reduction of the configuration space. For (2.6.6) to hold, it suffices to require
exp(K(s
1
+ s
3
)) + exp(−K(s
1
+ s
3
)) = f (K) exp(K
L
s
1
s
3
) (2.6.7)
for all choices of s
1
and s
3
. The solution to these equations is given by
K
L
= ln cosh(2K)/2, f(K) = 2 cosh
1/2
(2K) (2.6.8)
The first equation defines the renormalization group flow in the space of the model
parameters, here the value of K. We then have
Z(N, K) = f(K)
N/2
Z(N/2, K
L
). (2.6.9)
The renormalized Hamiltonian is
H
L
= −J
L
X
|i−j|=2
s
i
s
j
, (2.6.10)
where J
L
= k
B
T K
L
. From (2.6.9), we obtain
−ζ(K) =
1
2
ln f(K) −
1
2
ζ(K
L
). (2.6.11)
From (2.6.8), if we know the value of ζ at K, we can obtain the value of ζ at K
L
.
To analyze the dynamics of the renormalization group flow and the change of the free
energy along th e flow, we may proceed as follows. When K = 0, the partition function
is simply Z(N, 0) = 2
N
. Therefore for some small value of K, say 0.01, we may set
Z(N, 0.01) ≈ 2
N
. We then use the renormalization transformation (2.6.8) iteratively to
find the free energy at other values of K. For the 1D Ising model, th is approximation is
indeed quite good [?]. See Table 2.6.2 (from [?]).
Is a permission required in this case?

80 CHAPTER 2. ANALYTICAL METHODS
ζ(K)
K Renormalization group Exact
0.01 ln 2 0.693 197
0.100 334 0.698 147 0.698 172
0.327 447 0.745 814 0.745 827
0.636 247 0.883 204 0.883 210
0.972 710 1.106 299 1.106 302
1.316 710 1.386 078 1.386 080
1.662 637 1.697 968 1.697 968
2.009 049 2.026 876 2.026 877
2.355 582 2.364 536 2.364 537
2.702 146 2.706 633 2.706 634
In this example, the renormalized Hamiltonian (2.6.10) is in exactly the same form
as the Hamiltonian we began with, i.e. we were able to find values of f(K) and K
L
such that (2.6.7) is satified for all values of s
1
and s
3
and no approximations are needed.
This is rarely the case in general. Instead, one has to make approximations in order to
maintain some feasibility for the renormalization group analysis, as the next example
shows.
2.6.3 RG analysis of the two-dimensional Ising model
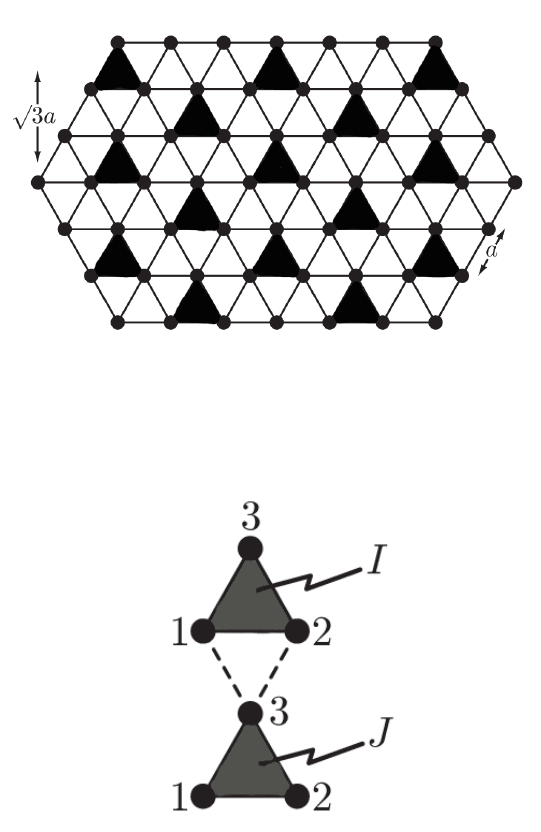
We now look at the Ising model on two-dimensional triangular lattice with lattice
constant a [?]. To coarse-grain the model, we divide the lattice into a triangular lattice
of triangular blocks indexed by I with three vertices inside each block, and define the
block spin S
I
= sgn(s
1
+ s
2
+ s
3
), where s
1
, s
2
, s
3
are the spins on the vertices inside the
I-th block, ordered in some particular way. After coarse-graining, the lattice constant
changes from a to
√
3a. When S
I
= 1, we have four possible spin configurations for s
1
,
s
2
and s
3
that we will denote by σ
I
= 1, 2, 3, 4: + + −, + −+, −+ + and + + +, where
we use + for spin up and − for spin down. These are the internal variables that we will
integrate over. To renormalize, note that we can write H as a function of the variables
{S
I
, σ
I
}: H = H(K, {S
I
, σ
I
}). Integrating out the variables {σ
I
}, we can write Z(K, N)
2.6. RENORMALIZATION GROUP ANALYSIS 81
in the form of
P
S
I
exp(−H(K
L
, {S
I
})) by taking
H(K
L
, {S
I
}) = −log
X
{σ
I
}
exp(−H(K, {S
I
, σ
I
})). (2.6.12)
It would be nice if H(K
L
, {S
I
}) has the same form as the original Hamiltonian, say
H = −J
L
P
hI,Ji
S
I
S
J
for some new parameter J
L
. However, this is impossible unless we
make some approximations.
Figure 2.7: Coarse-graining th e Ising model on triangular lattice.
Figure 2.8: Interaction between two block spins.

82 CHAPTER 2. ANALYTICAL METHODS
The starting point is
P {S
I
} =
X
{s
i
|S
I
}
P {s
i
} (2.6.13)
where
P
{s
i
|S
I
}
means summing over all configurations {s
i
} that give rise to {S
I
} after
coarse graining. For later use, we mention the obvious relation:
X
{s
i
}
=
X
{S
I
}
X
{s
i
|S
I
}
(2.6.14)
and the elementary but useful factorization:
X
x
1
···
X
x
n
f
1
(x
1
) ···f
n
(x
n
) = (
X
x
1
f
1
(x
1
)) ···(
X
x
n
f
n
(x
n
)) (2.6.15)
Rewriting (2.6.13), we have
e
K
L
P
S
I
S
J
P
{S
I
}
e
K
L
P
S
I
S
J
=
X
{s
i
|S
I
}
e
K
P
s
i
s
j
P
{s
i
}
e
K
P
s
i
s
j
(2.6.16)
In the last equation, K
P
|i−j|=1
s
i
s
j
consists of two parts: the part that corresponds to
the internal block, including all terms for which s
i
and s
j
are in the same block, and the
inter-block part that includes all terms for which s
i
and s
j
are in two different blocks.
We denote them by H
0
and H
1
respectively.
Claim: For (2.6.16) to hold, it is sufficient that
e
K
L
P
S
I
S
J
=
P
{s
i
|S
I
}
e
K
P
s
i
s
j
P
{s
i
|S
I
}
e
−H
0
/(k
B
T )
(2.6.17)
Proof. Note that
X
{s
i
|S
I
}
e
−H
0
/(k
B
T )
=
M
Y
I=1
X
σ
I
e
K(S
1
I
S
2
I
+S
2
I
S
3
I
+S
3
I
S
1
I
)
!
= (e
3K
+ 3e
−K
)
M
(2.6.18)
where M is the number of blocks. Note also that the right hand side of (2.6.18) does not
depend on {S
I
}. Summing over {S
I
} on both sides of (2.6.17), we get
X
{S
I
}
e
K
L
P
S
I
S
J
=
P
{s
i
}
e
K
P
s
i
s
j
P
{s
i
|S
I
}
e
−H
0
/(k
B
T )
where we used (2.6.14). The ratio of (2.6.17) and the last equation gives (2.6.16).

2.6. RENORMALIZATION GROUP ANALYSIS 83
Next define the weighted average:
hAi =
P
{s
i
|S
I
}
e
−H
0
/(k
B
T )
A
P
{s
i
|S
I
}
e
−H
0
/(k
B
T )
then (2.6.17) can be written as
e
K
L
P
S
I
S
J
= he
−H
1
/(k
B
T )
i = e
−hH
1
i/(k
B
T )−
1
2
(hH
2
1
i−hH
1
i
2
)/(k
B
T )
+ ··· (2.6.19)
We will make the approximation:
he
−H
1
/(k
B
T )
i ≈ e
−hH
1
i/(k
B
T )
(2.6.20)
This is a drastic approximation. Now compare the exponents:
−K
L
X
|I−J|=1
S
I
S
J
= hH
1
i/(k
B
T ) = −
X
|I−J|=1
K
hs
1
I
s
3
J
i + hs
2
I
s
3
J
i
where s
i
I
, s
j
J
are shown in Figure 2.6.3.
Using (2.6.15) again, we have
hs
1
I
s
3
J
i =
P
{s
i
|S
I
}
e
−H
0
/(k
B
T )
s
1
I
s
3
J
P
{s
i
|S
I
}
e
−H
0
/(k
B
T )
=
P
σ
I
e
K(s
1
I
s
2
I
+s
2
I
s
3
I
+s
3
I
s
1
I
)
s
1
I
P
σ
I
e
K(s
1
I
s
2
I
+s
2
I
s
3
I
+s
3
I
s
1
I
)
·
P
σ
J
e
K(s
1
J
s
2
J
+s
2
J
s
3
J
+s
3
J
s
1
J
)
s
3
J
P
σ
J
e
K(s
1
J
s
2
J
+s
2
J
s
3
J
+s
3
J
s
1
J
)
Similar to (2.6.18), we get
X
σ
I
e
K(s
1
I
s
2
I
+s
2
I
s
3
I
+s
3
I
s
1
I
)
s
1
I
= S
I
(e
3K
+ e
−K
)
Therefore, we have
K
L
X
|I−J|=1
S
I
S
J
=
X
|I−J|=1
2K(
e
3K
+ e
−K
e
3K
+ 3e
−K
)
2
S
I
S
J
namely,
K
L
= R(K) = 2K(
e
3K
+ e
−K
e
3K
+ 3e
−K
)
2
This is the renormalization group flow under the approximation (2.6.20).
The nontrivial fixed point of this map is K
∗
=
1
4
ln(1 + 2
√
2) ≈ 0.3356, from which
we also obtain ν = ln L/ ln R
′
(K
∗
) ≈ 1.134. As a comparison, note that Onsager’s exact
solution for the 2D Ising model on triangular lattice gives K
∗
=
1
4
ln 3 ≈ 0.2747 and
ν = 1.
In principle, we may try to improve upon the approximation (2.6.20). In practice,
this is not easy since the computation quickly becomes very involved.
84 CHAPTER 2. ANALYTICAL METHODS
2.6.4 A PDE example
Consider the example
∂
t
u
1
= ∂
2
x
u
1
− u
1
u
2
2
∂
t
u
2
= D∂
2
x
u
2
+ u
1
u
2
2
(2.6.21)
with initial data that decays sufficiently fast at infinity. This example was analyzed in
[?]. Our interest here is to see how simple-minded renormalization group methods can
be used for this problem.
First let us define the renormalization transformation. Let L > 1 be fixed, and let
(u
1
, u
2
) be the solution of (2.6.21). Define
˜u
1
(x, t) = L
α
1
u
1
(Lx, L
2
t)
˜u
2
(x, t) = L
α
2
u
2
(Lx, L
2
t)
(2.6.22)
Next, we define the renormalization group flow, now in the space of nonlinear opera-
tors. It is easy to see that (˜u
1
, ˜u
2
) satisfies
∂
t
˜u
1
= ∂
2
x
˜u
1
− L
2(1−α
2
)
˜u
1
˜u
2
2
∂
t
˜u
2
= D∂
2
x
˜u
2
+ L
2−(α
1
+α
2
)
˜u
1
˜u
2
2
(2.6.23)
Therefore, under the renormalization transformation (2.6.22), the operator in the PDE
changes to
∂
2
x
u
1
− u
1
u
2
2
D∂
2
x
u
2
+ u
1
u
2
2
−→
∂
2
x
u
1
− L
2(1−α
2
)
u
1
u
2
2
D∂
2
x
u
2
+ L
2−(α
1
+α
2
)
u
1
u
2
2
(2.6.24)
This suggests that we should consider the class of operators with the form
L
u
1
u
2
=
∂
2
x
u
1
+ c
1
u
1
u
2
2
D∂
2
x
u
2
+ c
2
u
1
u
2
2
(2.6.25)
Indeed, under the same renormalization transformation, such an operator changes to
˜
L
u
1
u
2
=
∂
2
x
u
1
+ c
1
L
2(1−α
2
)
u
1
u
2
2
D∂
2
x
u
2
+ c
2
L
2−(α
1
+α
2
)
u
1
u
2
2
(2.6.26)
which is still in the same class of operators. Therefore our renormalization group flow is
defined by:
c
1
→ c
1
L
2(1−α
2
)
, c
2
→ c
2
L
2−(α
1
+α
2
)
(2.6.27)

2.7. THE MORI-ZWANZIG FORMALISM 85
We are interested in the fixed points of the map (2.6.22) and (2.6.27). Fixed points
of (2.6.27) should satisfy
c
∗
1
= c
∗
1
L
2(1−α
2
)
, c
∗
2
= c
∗
2
L
2−(α
1
+α
2
)
(2.6.28)
It is beyond our scope to carry out a complete analysis of all the fixed points. But one
interesting set of fixed points identified by Bricmont et al. is given by [?]
c
∗
1
= −1, c
∗
2
= 0, α
2
= 1, α
1
> 1 (2.6.29)
This fixed point corresponds to the PDE
∂
t
u
1
= ∂
2
x
u
1
− u
1
u
2
2
∂
t
u
2
= D∂
2
x
u
2
(2.6.30)
The final step is to study the linearization of the renormalization group flow (2.6.27)
around this fixed point. We refer to [?] for some details. Let us note that this fixed point
PDE has solutions that are fixed point of the map (2.6.22). The value of α
1
can be found
by looking for solutions of (2.6.30) which are also fixed points of the renormalization
transformation (2.6.22). Such solutions must take the form
u
1
(x, t) = t
−
α
1
2
u
1
x
√
t
, u
2
(x, t) = t
−
1
2
u
2
x
√
t
It is easy to see that
u
2
(ξ) = Ae
−
ξ
2
4
and u
1
satisfies
−
d
2
u
1
dξ
2
−
1
2
ξ
du
1
dξ
−
α
1
2
u
1
+ u
2
2
u
1
= 0
For small values of A, α
1
can be calculated perturbatively, and it has the form [?]
α
1
= 1 +
A
2
4π
√
2D + 1
+ O(A
4
).
2.7 The Mori-Zwanzig formalism
So far we have discussed two special situations in which simplified effective models
can be obtained using asymptotic analysis. The first is the case when the system has

86 CHAPTER 2. ANALYTICAL METHODS
disparate scales. The second is when the system has self-similar behavior at different
scales. A natural question is: What happens in more general situations? To address this
question, we turn to the Mori-Zwanzig formalism.
The Mori-Zwanzig formalism is a strategy for integrating out a subset of variables
in a problem, which is precisely what we would like to do when performing coarse-
graining [?, ?]. What is remarkable about the Mori-Zwanzig formalism is its generality
– it applies to general nonlinear systems. However, at some level, it is also a tautology,
since what it does is simply to represent the solution for a subset of the variables (the
ones to be eliminated) as functionals of the other variables (the ones to be kept) and
then substitute back into the (projected form of the) original equation. In this way, some
variables are formally eliminated, but the remaining m odel is often far from being explicit.
Nevertheless, it is still a very good starting point for model reduction or coarse-graining
for the following reasons:
1. It is a general strategy.
2. It suggests the form of the reduced model. For example, if we start with the
equations in molecular dynamics, then the model obtained after elimination of
some variables can be viewed as a generalized Langevin equation, with noise and
memory terms.
3. It provides the starting point for making further approximations. From a practical
viewpoint, this is the most imp ort ant application of the Mori-Zwanzig formalism.
For example, the abstract generalized Langevin equation that arises from the appli-
cation of the Mori-Zwanzig formalism to molecular dynamics models can sometimes
be approximated by a much simpler Langevin equation.
We start with a simple example to illustrate the basic idea. Consider a linear system
dp
dt
= A
11
p + A
12
q, (2.7.1)
dq
dt
= A
21
p + A
22
q. (2.7.2)
Our objective is to obtain a closed model for p, which is the quantity that we are really
interested in. To this end, we solve the second equation for q, viewing p as a parameter:
q(t) = e
A
22
t
q(0) +
Z
t
0
e
A
22
(t−τ)
A
21
p(τ) dτ.
