Water and Wastewater Engineering

Подождите немного. Документ загружается.

13-8 WATER AND WASTEWATER ENGINEERING

where E  energy in each photon, J

h  Plank ’ s constant, 6.6  10



J · s

c  speed of light, m/s

  wavelength of radiation, m

In general, the more energy associated with a photon of electromagnetic radiation, the more

dangerous it is to living organisms.

Light photons with wavelengths longer than 1,000 nanometers (nm) have a photon energy

too small to cause chemical change when absorbed, and photons with wavelengths shorter than

100 nm have

so much energy that ionization and molecular disruptions characteristic of radiation

chemistry prevail.

Little photochemistry occurs in the near infrared range except in some photosynthetic bac-

teria. The visible range is completely active for photosynthes is in green plants and algae. The

ultraviolet range is divided into three

categories connected with the human skin’s sensitivity to

ultraviolet light. The UVA range causes changes to the skin that lead to tanning. The UVB range

can cause skin burning and is prone to induce skin cancer. The UVC range is extremely dangerous

since it is absorbed by proteins and can lead to cell mu

tations or cell death.

UV electromagnetic energy is typically generated by the flow of electrons from an electrical

source through ionized mercury vapor in a lamp. Several manufacturers have developed systems

to align UV lamps in vessels or channels to provide UV light in the germicidal range for inac-

tivation of bac

teria, viruses, and other microorganisms. The UV lamps are similar to household

fluorescent lamps, except that fluorescent lamps are coated with phosphorus, which converts the

UV light to visible light.

Disinfection Byproducts. Chlorine reacts with natural organic matter (NOM) to form a num-

ber of carcinogenic byproducts. These inc

lude but are not lim ited to trihalomethanes (THMs),

haloacetic acids (HAAs), haloacetonitriles, haloketones, haloaldehydes, chloropicrin, cyanogen

chloride, and chlorophenols. The THMs and HAAs occur most frequently and generally repre-

sent the highest concentrations of the organic contaminants.

Chloramines react with NOM to for

m byproducts similar to those formed by chlorination but

at lower concentrations (U.S. EPA, 1994).

TABLE 13-2

Spectral ranges of interest in photochemistry

Range name Wavelength range (nm)

Near infrared 700–1,000

Visible 400–700

Ultraviolet

UVA 315–400

UVB 280–315

UVC 200–280

Vacuum ultraviolet (VUV) 100–200

DISINFECTION AND FLUORIDATION 13-9

Chlorine dioxide and ozone can oxidize a number of organic constituents without producing

THMs or HAAs. However, chlorine dioxide itself and the chlorite ion are toxic. Approximately

70 percent of the chlorine dioxide consumed by oxidation reactions is converted to chlorite under

conditions typical in water treatment (Singer, 1992). In addition, if bromide is present, ozonation

will form the hypobromite ion (OBr



) which, in turn, forms, hypobromous acid that will react

with NOM to form brominated byproducts.

There are no known disinfection byproducts that result from UV radiation (Haas, 1999).

Chemical Disinfectant Kinetics

Although more complex models are available, it is often assumed that decay of chlorine, com-

bined chlorine, and chlorine dioxide can be modeled as a first order or pseudo-first order reac-

tion, that is:



(13-17)

where C  disinfectant concentration, mg/L

 first order decay rate constant, time



t  time, complementary units to k

E xample pseudo-first order decay rate constants are shown in Table 13-3 .

TABLE 13-3

Pseudo-first order decay rate constants

Compound

Condition Source

Ozone

1.5  10

4

1

Ground water low DOC

;

high alkalinity

Acero & von Gunten, 2001

Ozone

2.5  10

3

1

Surface water high DOC;

low alkalinity

Acero & von Gunten, 2001

Ozone

0.108 to 0.128 min

1

Ozone contact chamber Rakness, 2005

AOP

1.4 

3

1

Ground water low DOC;

high alkalinity

Acero & von Gunten, 2001

AOP 5.8  10

3

1

Surface water high DOC;

low alkalinity

Acero & von Gunten, 2001

Chloramine 0.01 to 0.02 d

1

Surface water TOC

1 to

2 mg/L

Wilczak et al., 2003

Chlorine 0.0011 to 0.0101 min

1

Surface water TOC 2.3 to

3.8 mg/L

Sung et al., 2001

Chlorine 0.71 to 11.09 d

1

Distrib. sys. pipe Clark et al., 1993

Chlorine 0.36 to 1.0 d

1

Distrib. sys. storage tank Rossman et al., 1995

Note that these authors presented these as first order approximations.

DOC  dissolved organic carbon.

AOP  advanced oxidation processes. These are combinations of disinfectants to produce hydroxyl radicals. Most

noteworthy of the AOP processes is ozone plus hydrogen peroxide.

TOC  total organic carbon.

13-10 WATER AND WASTEWATER ENGINEERING

H ypochlorite and ozone decay are modeled as a second order reaction (Gordon et al., 1995;

Gurol and Singer, 1982):



(13-18)

where k

2 d

 second order decay rate constant, L/mg · s

t  time, s

Example 13-3. Using the following data adapted from Gurol and Singer (1982), estimate the

rate constant for ozone decay at a pH of 2.2.

Ozone concentration, mg/L Time, min

14.0 0

12.9 20

11.3 60

9.96 100

9.38 120

Solution:

a . Integration of Equation 13-18 yields

ktC





()()()

b. A plot of



⎛

⎝

⎜

⎞

⎠

⎟

versus time yields a straight lline

with a slope equal to k

as shown in Figure 13-1 .

y  0.0003x  4E06

 0.9996

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

Time, min

1/concentration, L/mg

20 40 60 80 100 120 140

FIGURE 13-1

Ozone decay rate constant.

DISINFECTION AND FLUORIDATION 13-11

The transformed data are



⎛

⎝

⎜

⎞

⎠

⎟

,L/mg

Time, min

0.00609 20

0.01707 60

0.02897 100

0.03518 120

c. From Figure 13-1 , the equation of the line yields a slope ( k

2 d

) of 0.0003 L/mg · min.

Comments:

1 . The calculations, fit of the line to the data points, and equation of the line were per-

formed with a spreadsheet.

2. Rate constants at other pH values will be substantially different.

Chemical Oxidant Demand

The chlorine demand of a water is the difference between the amount of chlorine added and the

amount of free, combined or total chlorine remaining at the end of the contact period. A similar

definition may be used for chlorine dioxide or ozone. The demand is a function of the water

quality characteristics, pH, temperature of the water, amo

unt of oxidant applied, and the time of

contact.

Significant amounts of ammonia in the water react with chlorine to produce an unpleasant

taste and odor (T&O). One method for removing T&O is by the addition of chlorine in a process

called breakpoint chlorination. The reactions of chlorine and ammonia exhibited in breakpoint

chlorination are an illustration of chlorine demand

( Figure 13-2 ). The addition of chlorine results

in the reactions with ammonia described in Equations 13-5 , 13-6 , and 13-7 . With molar Cl

(as N), concentrations up to 1:1 (5:1 mass basis) monochloramine and dichloramine will be

formed. The relative amounts of each depend on pH and other factors. Chloramine residuals gen-

erally reach a maximum at equimolar concentrations of chlorine and ammonia. Further increas

in the Cl

:NH

ratio result in the oxidation of ammonia and reduction of chlorine. Sufficient time

must be provided to allow the reaction to go to completion. Chloramine residuals decline to a

minimum value, the breakpoint, when the molar Cl

:NH

ratio is about 2:1. At this point, the

oxidation/reduction reactions are essentially complete. Further addition of chlorine produces free

chlorine.

Other demand reactions are not s o dramatic as breakpoint chlorination. Significant concen-

trations of strong reducing compounds that react rapidly will yield a demand

curve such as that

for sulfur dioxide ( Figure 13-3 ). Lower concentrations of compounds such as NOM react slowly.

The demand of these compounds is determined by comparison of their rate of decay to the rate of

decay of the oxid

ant in pure water under identical conditions.

13-12 WATER AND WASTEWATER ENGINEERING

Mechanisms of Disinfection

The mode of action by which disinfec tants inactivate or kill microorganisms is dependent on a

large number of variables. This brief overview is limited to some of the common water disinfec-

tants and two broad classes of microorganisms: bacteria and viruses.

Chlorine dose, mg/L

Immediate demand

Residual chlorine, mg/L

Chlorine applie

Chlorine

ure

FIGURE 13-3

Chlorine demand exhibited by a very fast reaction such as that with sulfur

dioxide.

Breakpoint

Combined chlorine

residuals in predominance

Free

chlorine residual

predominant

Chlorine dosage, mg/L

Residual chlorine, mg/L

0.5 1.0 1.5

Mole ratio (Cl

:NH

-N)

2 3 4 5 67891011

Chlorine applie

curve

FIGURE 13-2

Breakpoint chlorination. ( Source: AWWA, 1969.)

DISINFECTION AND FLUORIDATION 13-13

Chlorine. The chlorine must penetrate into the bacterial cell to cause inactivation. In bacteria,

respiratory, transport, and nucleic acid activity are all adversely affected (Haas and Engelbrecht,

1980). In bacteriophage, the mode of action appears to be disruption of the viral nucleic acid,

while in poliovirus the protein coat is affected (Dennis et al., 1979; Fujioka et al., 1985).

Chlorine Dioxide. The physiologic al mode of inactivation is attributed to disruption of pro-

tein synthesis (Benarde et al., 1967). Disruption of capsid functions inactivates viruses (Noss

et al., 1985) .

Ozone. Although complicated by measurement difficulties, physicochem

ical damage to DNA

appears to be the mechanism of inactivation of both bacterial cells and poliovirus (Hammelin

and Chung, 1978; Roy et al., 1981). This includes attack on the bacterial membrane, disruption

of enzymatic activity, and nucleic acids. The first site for virus inactivation is the virion capsid

(U.S. EPA, 1999).

UV Radiation.

UV radiation causes specific deleterious changes in microorganism nucleic

acids. (Jagger, 1967). DNA absorbs light in the ultraviolet range—primarily between 200 and

300 nanometers (nm). UV light is most strongly absorbed by DNA at 253.7 nm. If the DNA

absorbs too much UV light, it will be damaged and will be unable to replicate. It has

been found

that the energy required to damage the DNA is much less than that required to actually destroy

the organism (Setlow, 1967). The effect is the same. If a microorganism cannot reproduce,

it cannot cause an infection.

Disinfection Kinetics

Chick’s Law. Using disinfectants like phenol, mercuric chloride, and silver nitrate and or-

ganisms like Salmonella typhi, Escherischia coli, Staphyloccus aureus, and Bacillus anthracis,

Dr. Harriet Chick demonstrated that disinfection could be m odeled as a pseudo-first order reac-

tion with respect to the concentration of organisms (Chi

ck, 1908). In a thoroughly mixed batch

reactor or a perfect plug flow reactor, Chick’s law takes the form



(13-19)

where N  number of organisms per unit volume

 rate constant of inactivation, s



, or min



t  time, s, or min

In integrated form the equation is

⎛

⎝

⎜

⎞

⎠

⎟



(13-20)

where N

 number of organisms per unit volume at time zero

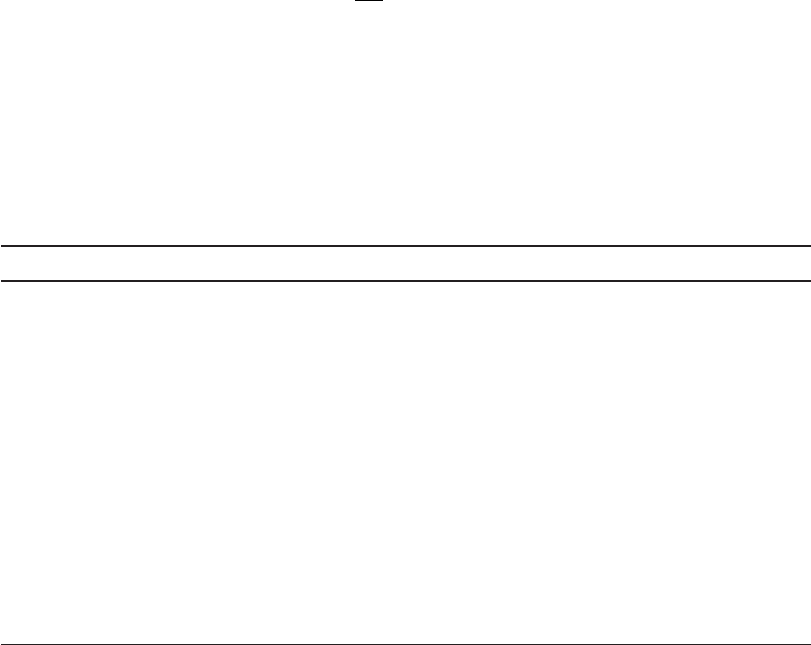
A common method of graphing the data for Chick’s law is to plot the log of the survival ratio

versus time on a semilog graph ( Figure 13-4 ).

13-14 WATER AND WASTEWATER ENGINEERING

Chick-Watson Law. Chick’s law does not take into account the concentration of the disin-

fectant. From Figure 13-4 , it is obvious that the disinfectant concentration has a marked effect.

Recognizing this, Watson (1908) proposed an alternative expression to describe a given level of

inactivation:

 constant

(13-21)

where C  disinfectant concentration, mg/L

n  coefficient of dilution

t  time

Chick’s law and Watson’s equation are combined by relating the rate constant of inactivation to

the disinfectant concentration:

kkC

ccw



(13-22)

where k

 rate constant of inactivation independent of concentration, time

 1

The Chick-Watson law in integrated form is then

kCt

⎛

⎝

⎜

⎞

⎠

⎟



(13-23)

Treatment time, sec

3

2

Log

PFU survival ratio

1

4

8121620

Treatment time, sec

Log

PFU survival ratio

20468

(a)

(b)

3

2

1

4

FIGURE 13-4

Inactivation of single poliovirus particles by HOCl ( a ) at 10  C, pH 6.0: () 1.5  M, () 11  M, () 20  M, and () 41  M; ( b ) at 20  C, pH 6.0: ()

2.2  M, () 11  M, () 22  M, and () 35  M. ( Source: Floyd, et al., 1979. )

DISINFECTION AND FLUORIDATION 13-15

Example 13-4. The data for HOCl disinfection of poliovirus at a c oncentration of 1.8 mg/L

is shown below (adapted from Floyd et al., 1979) . The temperature was 20  C, the pH was 6.0.

Determine the rate constant of inactivation assuming the Chick-Watson model applies with an n

value of 1.0.

Time, s

Number of PFU

0 6,152

2 3,000

4 1,200

6 710

8 300

P FU  plaque forming units.

Solution:

a . Compute ln( N / N

) and Ct for each time.

Time, s

ln(N/N

) Ct

0 0.0 0

2 0.718 3.6

4 1.63 7.2

6 2.16 10.8

8 3.02 14.4

b. A “trendline” fit of ln( N / N

) versus Ct yields a straight line with a slope equal to k

a s

shown in Figure 13-5 .

c. From a spreadsheet, the equation of the trend line yields a slope of 0.2078 and k

0.2078 L/mg · s.

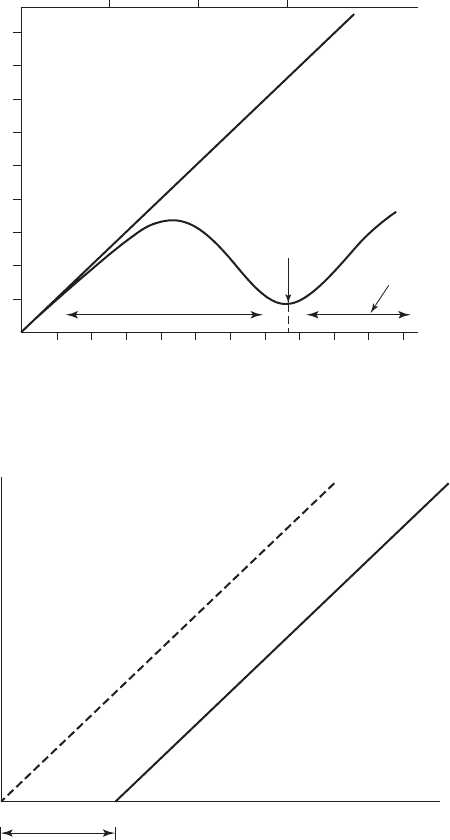
y = 0.2078x  0.0092

 0.9953

3.5

3

2.5

2

1.5

1

0.5

0246

10 12 14 16

Ct, mg·s/L

ln(N/N

)

FIGURE 13-5

Poliovirus decay rate.

13-16 WATER AND WASTEWATER ENGINEERING

The Chick-Watson law assumes that the concentration of disinfectant remains constant. As

noted above, even without reaction with other constituents in the water, the disinfectant con-

centration decays with time. Even if the concentration is kept constant during inactivation of

microorganisms, the resu lts do not always follow Equation 13-23

. “Tailing,” “should ers,” and

time lags may occur with different microorganism and disinfectant combinations. Different tem-

peratures and pH values for the same organism and disinfectant will result in different curves as

shown in Figures 13-4a and 13-4b .

In many

cases the exponent “ n ” in Equation 13-22 is close to 1.0 (Hoff, 1986). Thus, a fixed

value of the product Ct results in a fixed degree of inactivation.

Plotting combinations of disinfectant concentration and time to a fixed percent inactivation

for a given temperature yields curves that follow the form of C

t  constant. The constant is a func-

tion of the organism, temperature, and pH. The curves are linear on a log-log scale ( Figures 13-6 A,

13-6B, and 13-6C).

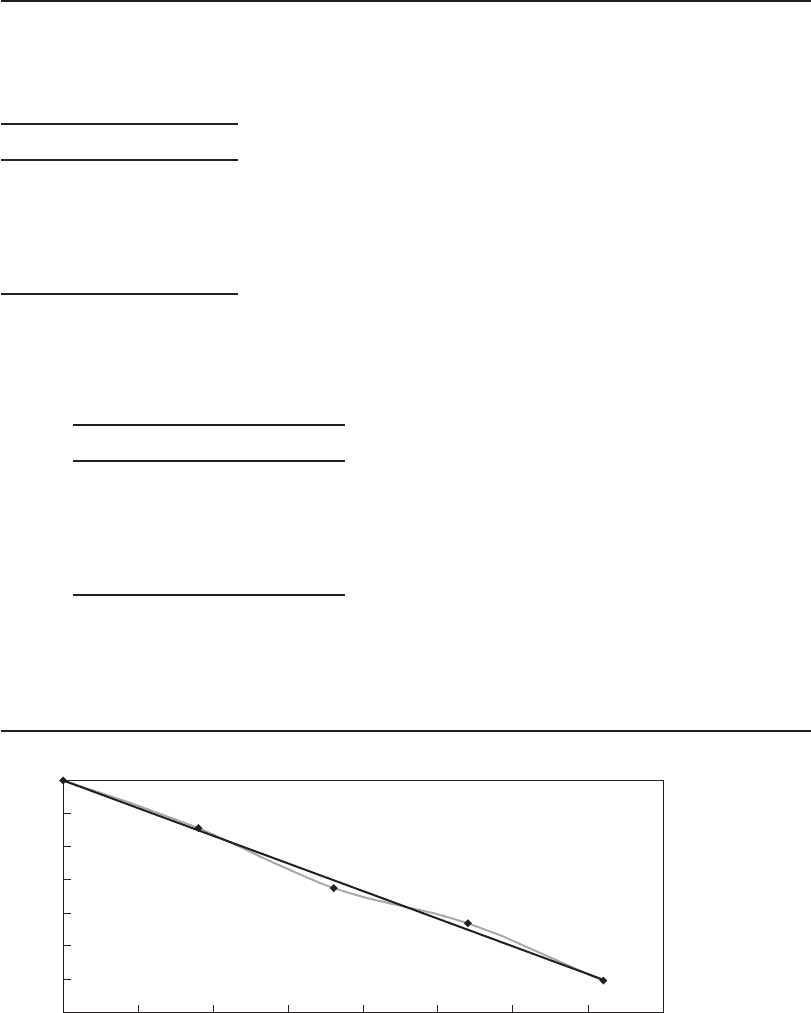
0.1

Free available chlorine, mg/L

(a)

100

1000

Time, min

E. histolytica

Polio type 1

E. coli

Giardia

FIGURE 13-6A

Free available chlorine disinfection. Time to achieve 99.6 to 100 percent

kill at water temperature of 0C to 5  C.

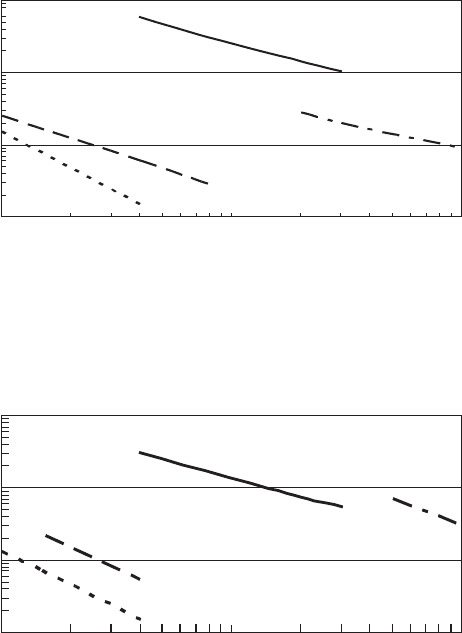
FIGURE 13-6B

Free available chlorine disinfection. Time to achieve 99.6 to 100 percent kill at

water temperature of 10  C.

0.1

(b)

Free available chlorine, mg/L

100

1000

Time, min

E. histolytica

Polio type 1

E. coli

Giardia

DISINFECTION AND FLUORIDATION 13-17

Hom-Haas Model. This model of disinfection accounts for both changes in chemical disinfec-

tant concentration and microorganism survival. The integrated form of the model is (Hom, 1972;

Haas and Joffe, 1994):

kCt

⎛

⎝

⎜

⎞

⎠

⎟



(13-24)

where k

 die-off coefficient, consistent units, for example: L/mg · s

n, m  empirical constants, dimensionless

M ultiple linear regression using survival as the dependent variable and disinfectant concentration

and time as the independent variables prod uces an inter

cept equal to k

and slopes equal to n

and m. This computation can be solved with the aid of a spreadsheet program.

UV Disinfection Kinetics. A modified form of the Chick-Watson law that includes the effects

of the wavelength of light can be used to describe survival of microorganisms exposed to UV

radiation (Linden and Darby, 1997; MWH, 200

5):



{}

(13-25)

where I



 effective germicidal intensity of UV radiation for wavelength , mW/cm

For multiple wavelengths, I



must be integrated over the spectrum of wavelengths. A plot of the

relationship between log survival of MS2 phage and effective germicidal dose [that is the product

of energy per unit area and time (mW/cm

)( t )] is shown in Figure 13-7 .

The inactivation of microorganisms by UV is directly related to UV dose. This is a concept

similar to Ct used for other common disinfectants, including chlorine and ozone. The average UV

dose is calculated as follows:

DIt



(13-26)

where D

 UV dose

I  average intensity, mW/cm

t  average exposure time, s

FIGURE 13-6C

Free available chlorine disinfection. Time to achieve 99.6 to 100 percent kill at

water temperature of 20C to 24  C.

100

1000

0.1

Free available chlorine, mg/L

Time, min

E. coli

Polio Type 1

Giardia

E. histolytica