Water and Wastewater Engineering
Подождите немного. Документ загружается.

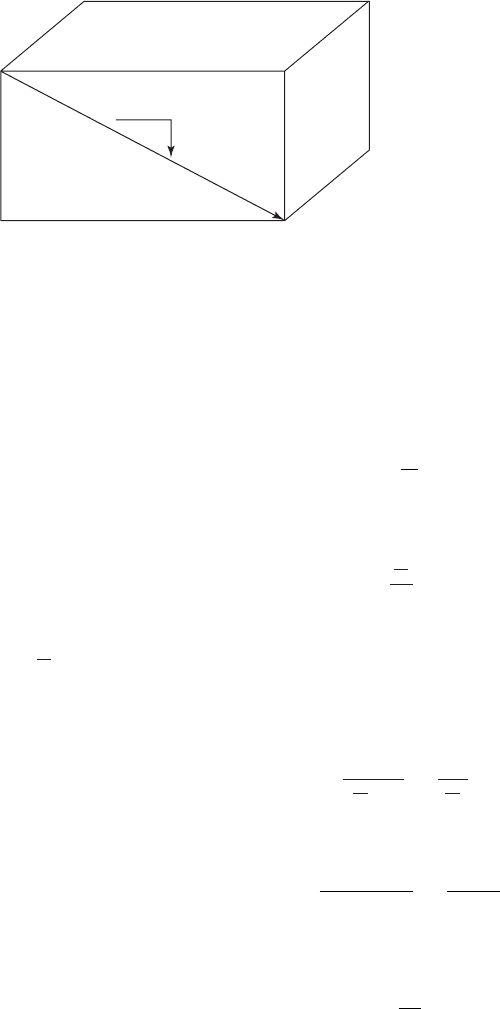
10-10 WATER AND WASTEWATER ENGINEERING
that it reaches the bottom of the tank during the time ( t
o
) the water spends in the tank (the deten-
tion time ). That is, the settling velocity must equal the depth of the tank divided by t
o
v
h
t
s
o
(10-14)
where the detention time is defined as
t
o
Q
V
(10-15)
where
V volume
of tank, m
3
Q flow rate, m
3
/ s
U sing the definition of detention time from Equation 10-15 and substituting into Equation 10-14 :
v
h
Q
hQ
s
()/
V
V
(10-16)
Because tank volume is described by the product of the height, length, and width
v
hQ
lwh
Q
lw
s
(10-17)
The product ( l w ) is the surface area ( A
s
). Therefore,
v
Q
A
s
s
(10-18)
which is the overflow rate ( v
o
). From this, Camp proposed that the overflow rate is the critical
design parameter that determines the removal efficiency of settling tanks. From a theoretical
w
h
l
v
s
v
0
FIGURE 10-6
D i mensional definition of settling zone for Camp’s deriva-
tion of overflow rate for a rectangular horizontal-flow sedi-
mentation tank.
SEDIMENTATION 10-11
perspective, this implies that the removal efficiency is independent of depth and hydraulic
detention time.
In a similar fashion to an upflow clarifier, if the settling velocity of a particle is equal to or
greater than the overflow rate, 100 percent of the particles will be captured in a horizontal sedi-
mentation tank. Unlike an upflow clarifier, some percentage of the particles with a v
s
less than v
o
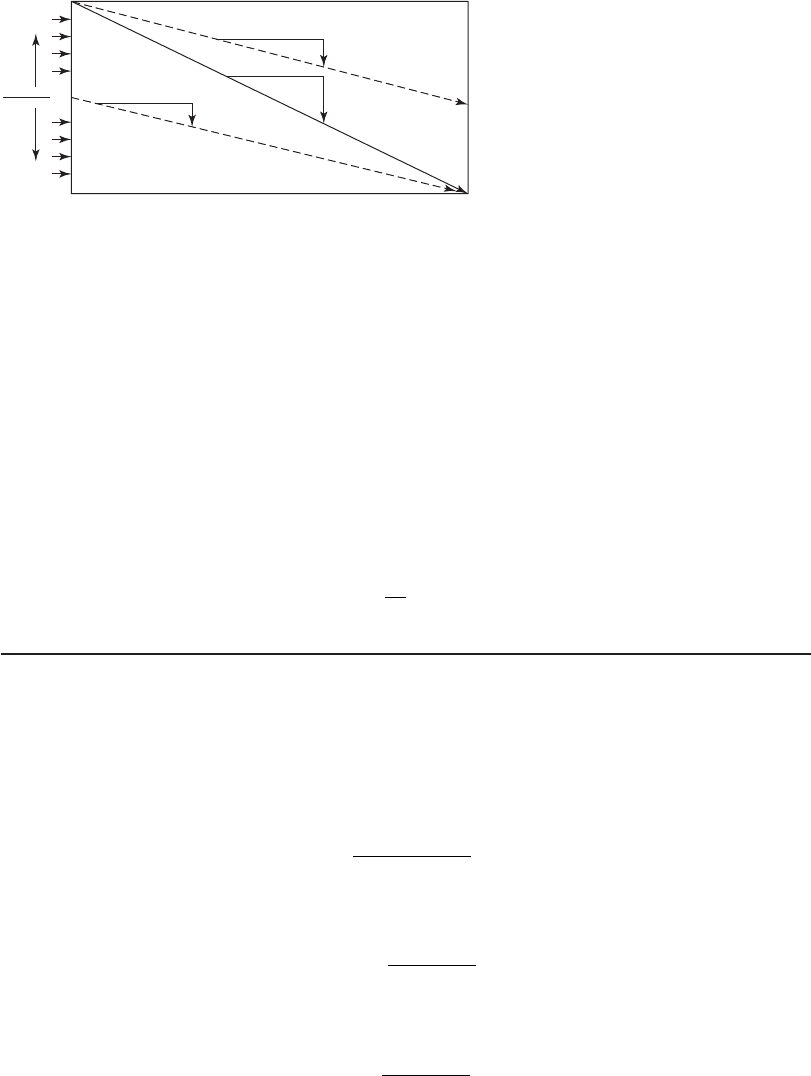
will be removed. For example, consider particles having a settling velocity of 0.5 v
o
entering uni-
formly into the settling zone. Figure 10-7 shows that 50 percent of these particles (those below
half the depth of the tank) will be removed. Likewise, one-fourth of the particles having a settling
velocity of 0.25 v
o
will be removed. The percentage of particles removed, P, with a settling ve-
locity of v
s
in a horizontal flow sedimentation tank designed with an overflow rate of v
o
is
P
v
v
%
s
o
⎛
⎝
⎜
⎞
⎠
⎟
100
(10-19)
Example 10-2. Sleepy Hollow has an existing horizontal-flow sedimentation tank with an over-
flow rate of 17 m
3
/ d · m
2
. What percentage removal should be expected for each of the following
particle settling velocities in an ideal sedimentation tank: 0.1 mm/s, 0.2 mm/s, and 1 mm/s?
Solution:
a . Begin by computing the overflow rate in compatible units.
()17
1 000
86 400
0
3 2
m /dm
mm/m
s/d
,
,
.
⎛
⎝
⎜
⎞
⎠
⎟
1197 0 2or mm/s.
b. For the 0.1 mm/s particles
P%%
01
02
50
.
.
mm/s
mm/s
(100 )
c. For the 0.2 mm/s particles
P%%
02
02
100 100
.
.
mm/s
mm/s
()
50% 50%
Escape
Ca
p
ture
d
v
0
/2
v
0
/2
v
0
FIGURE 10-7
Partial particle removal in an ideal sedimentation tank. ( Source: Davis and Cornwell,
2008.)

10-12 WATER AND WASTEWATER ENGINEERING
d. For the 1 mm/s particles
P%
1
02
500
mm/s
mm/s
(100%)
.
But the particle removal cannot be greater than 100%, so the particle removal is 100%
for the particles settling at 1 mm/s.
Type II Sedimentation
T ype II sedimentation is characterized by particles that flocculate during sedimentation. These
types of particles occur in alum or iron coagulation, in wastewater primary sedimentation, and in
settling tanks in trickling filtration.
There is no adequate mathematical relationship that can be used to desc
ribe Type II settling.
The Stokes equation cannot be used because the flocculating particles are continually changing in
size and shape. In addition, as water is entrapped in the floc, the specific gravity also changes.
Settling Column Model. Laboratory tests with settling columns serve as a model of the behavior
of flocculant settling. These have valu
e in evaluating of existing settling tanks and in developing
data for plant expansion or modification of existing plants, but are not practical for the design
of new settling tanks because of the difficulty in replicating the properties and concentrations of
particles coming from the coagulation/flocculation process. The following discussion illu
strates
both the method of analyzing the column data and the behavior of the flocculant suspension.
A settling column is filled with the suspension to be analyzed. The suspension is allowed to
settle. Samples are withdrawn from sample ports at different elevations at selected time intervals.
The concentration of suspend
ed solids is determined for each sample and the percent removal is
calculated:
R%
C
C
%
t
1 100
0
⎛
⎝
⎜
⎞
⎠
⎟
()
(10-20)
where R % percent removal at one depth and time, %
C
t
concentration at time, t, and given depth, mg/L
C
0
initial concentration, mg/L
Percent removal versus depth is then plotted as shown in Figure 10-8 . The circled numbers are
the calculated percentages. Interpolations are made between these plotted points to construct
curves of equal concentration at reasonable percentages, that is, 5 or 10 percent increm
ents.
Each intersection point of an isoconcentration line and the bottom of the column defines an
overflow rate ( v
o
):
v
H
t
o
i
(10-21)
where H height of column, m
t
i
t i me defined by intersection of isoconcentration line and bottom of column ( x -axis)
where the subscript, i, refers to the first, second, third, and so on intersection points
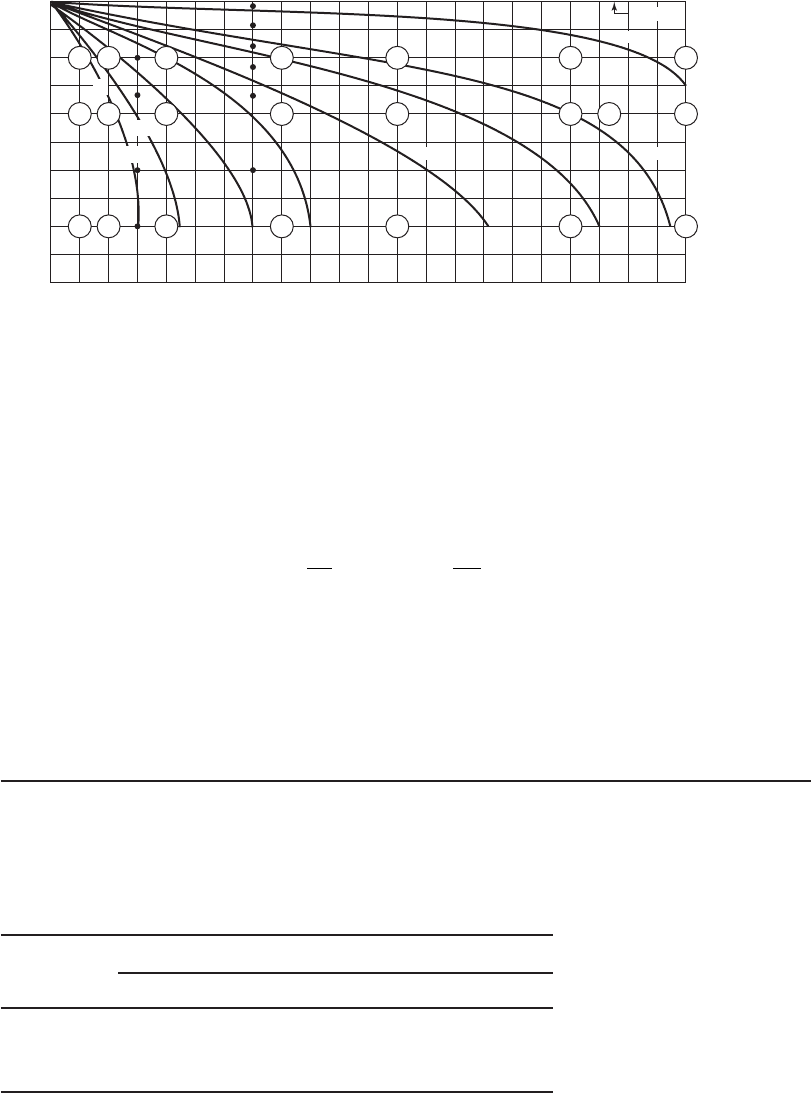
SEDIMENTATION 10-13
A vertical line is drawn from t
i
to intersect all the isoconcentration lines crossing the t
i
time. The
midpoints between isoconcentration lines define heights H
1
, H
2
, H
3
, and so on used to calculate
the fraction of solids removed. For each time, t
i
, defined by the intersection of the isoconcentra-
tion line and the bottom of the column ( x -axis), a vertical line is constructed and the fraction of
solids removal is calculated:
RR
H
H
RR
H
H
RR
Ta ba cb
0
12
()()…
(10-22)
where
R
T
0
total
fraction removed for settling time, t
a
R
a
, R
b
, R
c
isoconcentration fractions a, b, c, etc.
The series of overflow rates and removal fractions are used to plot two curves. One of suspended
solids removal versus detention time and one of suspended solids removal versus overflow rate.
These can be used to size the s
ettling tank. Eckenfelder (1980) recommends that scale-up factors
of 0.65 for overflow rate and 1.75 for detention time be used to design the tank.
Example 10-3. The city of Stillwater is planning to ins tall a new settling tank as an upgrade
to their existing water treatment plant. Design a settling tank to remove 65% of the influent sus-
pended solids from their design flow of 0.5 m
3
/ s. A batch-settling test using a 2.0 m column and
coagulated water from their existing plant yielded the following data:
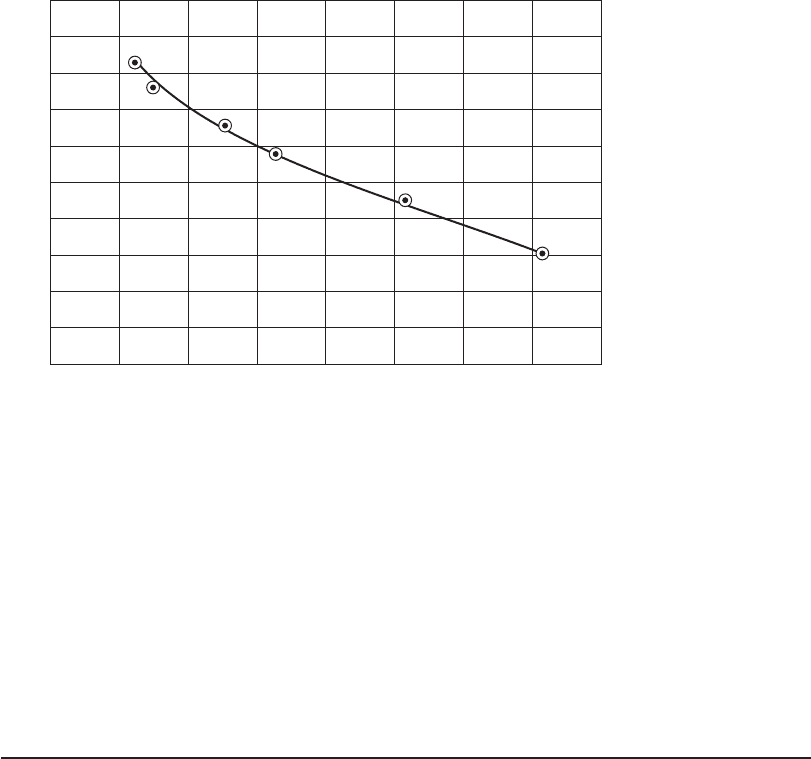
Percent removal as a function of time and depth
Sampling time, min
Depth, m510 20 40 60 90 120
0.5 41 5060677273 76
1.0 19 33 45586270 74
2.0 1531 38 54 5963 71
Sampling time, min
20 3040506070809010012010
2.0
Depth, m
1.5
1.0
0.5
0.0
50
59 63 715438
40% 50% 55%65%
3115
19 33 45 58 62 70 74 74
73 767267605041
H
3
H
2
H
1
t
a
R
c
R
a
R
b
30% 60% 70%
75%
100%
FIGURE 10-8
I soconcentration lines for Type II settling test using a 2-m-deep column.
10-14 WATER AND WASTEWATER ENGINEERING
Solution. The plot is shown in Figure 10-8 .
a . Calculate the overflow rate for each intersection point. For example, for the 50% line,
v
o
20
35
1 440 82 3
.
,.
m
min
min/dm()
b. The corresponding removal percentage is
R
T 50
50
1 5
20
55 50
085
20
60 55
060
2
.
.
.
.
.
.
()()
00
65 60
040
20
70 65
020
20
75 70
00
()()
()
.
.
.
.
.
55
20
100 75
59 5 60
.
.
()
or %
c. The corresponding detention time is taken from the intersection of the isoconcentration
line and the x -axis used to define the overflow rate, that is, 35 minutes for the 50% line.
d. This calculation is repeated for each isoconcentration line that intersects the x -axi
s,
except the last ones for which data are too sparse, that is, 30, 40, 50, 55, 60, and 65%, but
not 70 or 75%.
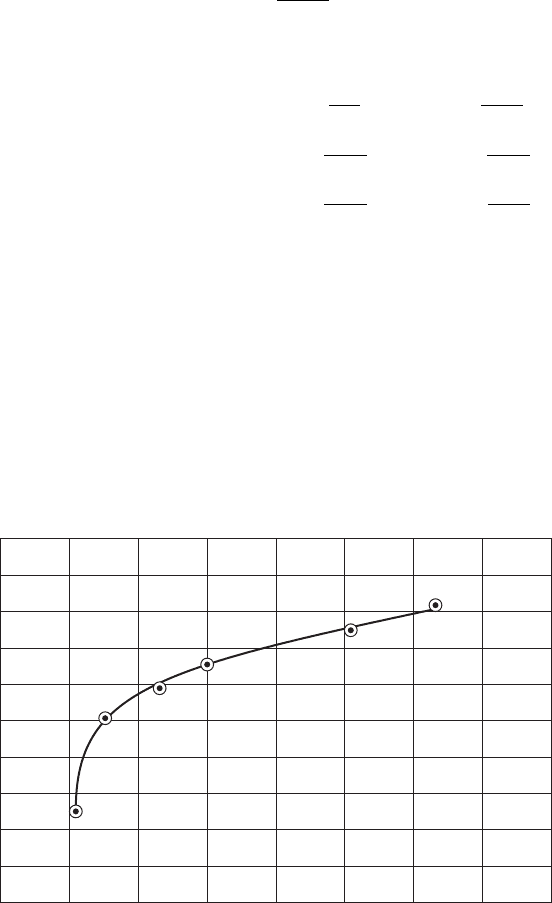
e. Two graphs are then constructed (see Figures 10-9 and 10-10 ). From these graphs the
bench-scale detention time and overflow rate for 65% removal are found to be 54 min-
utes and 50 m/d.
Detention time, h
Suspended solids removal, %
0.5
30
40
50
60
70
80
0 1.0 1.5 2.0
FIGURE 10-9
S uspended solids removal versus detention time. ( Source: Davis and Cornwell, 2008.)
SEDIMENTATION 10-15
Overflow rate, m/d
Suspended solids removal, %
50
30
40
50
60
70
80
0 100 150 200
FIGURE 10-10
S uspended solids removal versus overflow rate. ( Source: Davis & Cornwell, 2008.)
f. Applying the scale-up factors yields
t
v
o
o
()()
()
54175 94 5 95
50
min or min
m/d
..
(()06532 5.. m/d
Comments:
1 . As implied by the shape of the isoconcentration lines, and, conceptually, the trajectory of
the particles, the settling velocity increases as the particles travel through the tank.
2. The depth of the tank is important because flocculant particles tend to grow in size.
Thus, a greater depth facilitates the growth process.
Type III and Type IV Sedimentation
When the water contains a high concentration of particles (for example, greater than 1,000 mg/L)
both Type III ( hindered settling or zone settling) and Type IV ( compression settling) occur along
with discrete and flocculant settling. Zone settling occurs in lime-softening sedimentation, activated-
sludge sedimentation, and sludge thickeners.
When a con
centrated suspension of uniform concentration is placed in a column or graduated
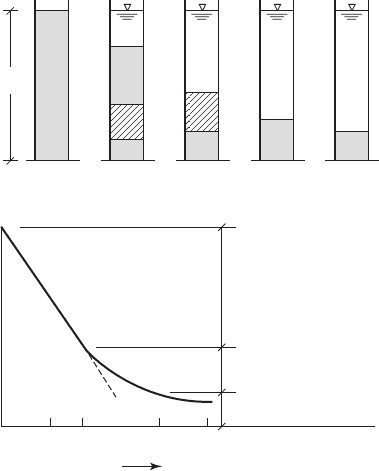
cylinder, Type II, III, and IV take place over time as illustrated in Figure 10-11 . With a high par-
ticle concentration the free area between the particles is reduced. This causes greater interparticle
fluid velocities that reduce the settling velo
city below that of the individual particles. Because of
the high concentration of particles, the liquid tends to move up through the interstices between
the particles. As a result, the particles that are in contact with one another tend to settle as a zone
or “blanket.” The particles in contact tend to maintain the same relative position. This results in a
relatively clear lay
er above the settling mass of settling particles. This phenomenon is known as
10-16 WATER AND WASTEWATER ENGINEERING
hindered settling. The rate of hindered settling is a function of the concentration of the particles
and their characteristics.
A s settling continues, a compressed layer of particles begins to form. The particles are in
contact and d o not really settle. A more correct way to visualize the phenomena is the flow of
water ou
t of a mat of particles that is being compressed. Thus, it is called compression settling.
A s with Type II settling, the methods for analyzing hindered settling require settling test
data. These methods are appropriate for plant expansions or modifications but have not found
use in the design of small treatment plants . The methods
are described in detail in Chapters 15
and 25.
High-Rate Settling. Increasing the particle density, or reducing the distance a particle must fall
prior to removal, can accelerate the clarification process.
The specific gravity of alum floc is approximately 1.001 and that of lime floc is 1.002
(Kawamura, 2000). Several proprietary pro
cesses add a ballast (usually mic rosized sand 20 to
200 m diameter) with a specific gravity on the order of 2.5 to 2.65 to the floc to increase its set-
tling velocity. The sand is recovered and reused.
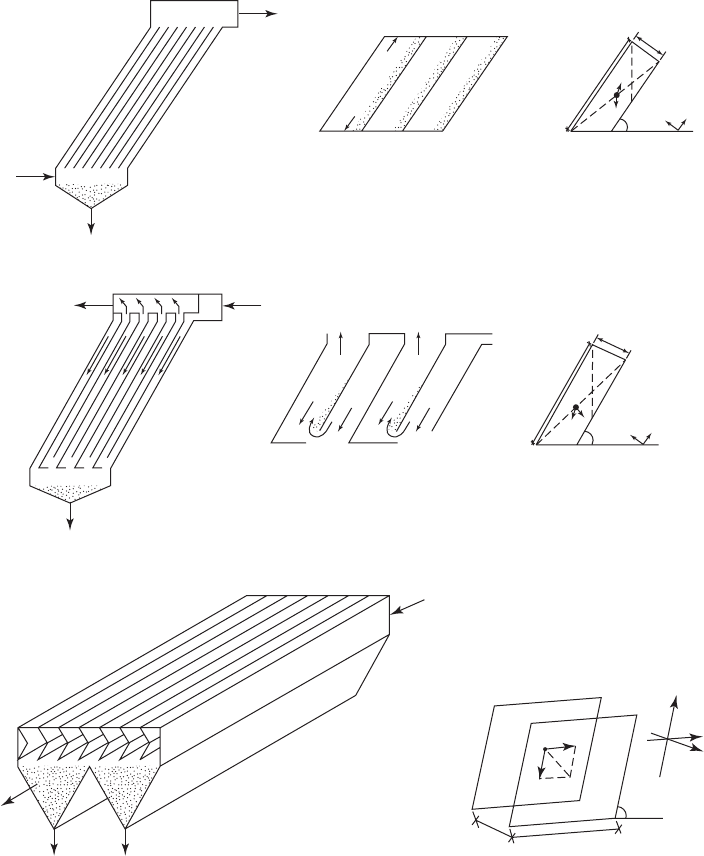
To reduce the distance the particle must fall, a series
of inclined plates or tubes are placed in a
rectangular horizontal flow settling basin. Three typical configurations are shown in Figure 10-12 .
The plates or tubes are inclined to a degree that allows the collected solids to slide down the sur-
face to the sludge zone. Typically the tube is a square, about 5 c
m on each side, and the angle is
FIGURE 10-11
I dealized schematic of Type III and IV settling in a column ( a ) and
a graph of the corresponding settling curve ( b ). ( Source: Metcalf
and Eddy, 2003.)
HS
HS
Slope settling
velocity
CS
CS
CS
t 0
H
(a)
(b)
Hindered (zone)
settling (HS)
Transition settling (TS)
Compression settling (CS)
Height of interfaceHeight of interface
Time
t t
1
t t
2
t t
3
t t
4
ws
TS
TS
TS
TS
t
1
t
2
t
3
t
4
CS
SEDIMENTATION 10-17
about 60 . The configurations are named to reflect the direction of flow of water with respect to
the direction that the particles will leave the plates or tubes: countercurrent, cocurrent, and cross-
current. Thus, for example, the countercurrent configuration is one in which the flow of water is
in the opposite direction to that of the particles.
Influent
Solids
T
u
rbl
d
wat
er
Effluent
Solids
(a)
Effluent
Influent
Solids
(b)
Soli
ds
T
u
rbid
water
T
u
rbi
d
water
L
p
d
y
x
Influent
y
x
z
v
fc
v
s
L
p
d
Effluent
Solids Solids
(c)
L
p
v
s
v
fc
d
yx
Soli
ds
v
s
v
fc
FIGURE 10-12
Flow patterns for inclined settling systems ( a ) countercurrent, ( b ) cocurrent, ( c ) crosscurrent.

10-18 WATER AND WASTEWATER ENGINEERING
The following theoretical development is from MWH (2005). The settling time for a particle
to move between countercurrent parallel plates is
t
d
v
s
cos
(10-23)
where t settling time, s
d distance between two parallel plates (as shown in Figure 10-12 ), m
v
s
particle settling velocity, m/s
inclination angle of plates from horizontal, degrees
If a uniform velocity is assumed, then the particle travel time spent in the plates is
t
L
vv
p
p
fc s
sin
(10-24)
where t
p
particle travel time spent in plates, s
L
p
length of plate, m
v
fc
fluid velocity in channel, m/s
If the trajectory of a particle that is shown in Figure 10-12 is considered, then all of the par-
ticles with a settling velocity v
s
are removed. If Equation 10-23 i s equated to Equation 10-24 , t
p
i s
equal to the settling time t. Those particles with a larger settling velocity are also removed, that is
v
vd
Ld
s
fc
p
cossin
(10-25)
The fluid velocity, v
fc
, may be determined from the number of channels
v
Q
Ndw
fc
(10-26)
where Q flow rate, m
3
/ s
N number of channels, dimensionless
w width of channel, m
If one assumes that the surface area of the basin is comprised of plates and that the area occu-
pied by the plates is ignored, then the fluid velocity, v
fc
, is also related to the overflow rate of the
basin
v
Q
Ndw
Q
A
fc
sin
(10-27)
where A top area of basin, m
2
.
Depending on where they enter the plate, particles with settling velocities less than v
s
may
also be removed.

SEDIMENTATION 10-19
For cocurrent settling, the settling time for a particle to move between two parallel plates is
given by Equation 10-23 . The time that particles moving with the fluid spend in the plates is
t
L
vv
p
p
fc s
sin
(10-28)
If Equation 10-23 i s equated to Equation 10-28 , t
p
i s equal to the settling time t. Those particles with a
settling velocity v
s
are removed. Those particles with larger settling velocity are also removed, that is
v
vd
Ld
s
fc
p
cossin
(10-29)
For crosscurrent settling, the settling time for a particle to move between two parallel plates is
also given by Equation 10-23 . The time that particles moving with the fluid spend in the plates is
t
L
v
p
p
fc
(10-30)
If t
p
i s equal to the settling time (equating Equation 10-23 and Equation 10-30 ), then the
particles with settling time v
s
are removed. Those particles with a larger settling velocity are also
removed, that is
v
vd
L
s
fc
p
cos
(10-31)
Non-Ideal Behavior of Settling Tanks
N umerous factors affect settling tank performance. These include turbulence, inlet energy dissipa-
tion, density currents, wind effects, outlet currents, and sludge equipment movement. In general, for
most water treatment sedimentation basins, performance is primarily
a function of turbulence, inlet
energy dissipation, density currents, and wind effects rather than outlet currents and mechanical
movement. Therefore, this discussion is focused on these effects.
Turbulence. In Camp’s development of a theoretical basis for removal of discretely s
ettling
particles he assumed a uniform horizontal velocity in the settling zone. This assumption implies
near laminar flow conditions (Reynolds number 1). This is rarely, if ever, achieved in actual
settling tanks. However, this important assumption is considered in the design of the tank by
evaluation of the Reynolds nu m
ber and the Froude number. These dimensionless ratios are
described in the next section of this chapter.
The Reynolds number is important as a measure of turbulence in flows that are influenced by
viscous effects, such as internal flows and boundary la
yer flows. The Froude number is important
in flows that are influenced by gravity, such as free surface flows.
Inlet Energy Dissipation. The performance of the sedimentation basin is strongly influ enc ed
by the effectiveness of energy dissipation at the inlet. Again using Camp’s theory, the flow must
