Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach

Подождите немного. Документ загружается.

234 CHAPTER 7 Averaging Schemes for Polyhedral Meshes



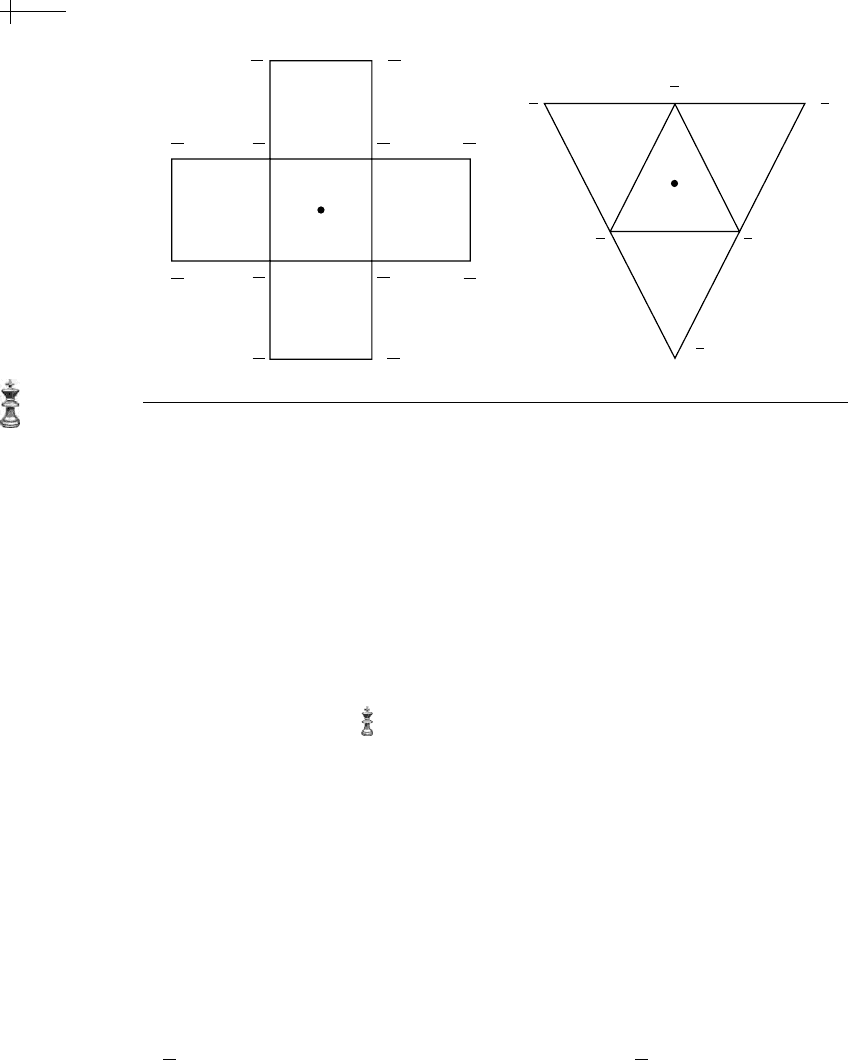
Figure 7.30 Subdivision rules for interpolatory face-splitting subdivision.

subdivision over edge-splitting subdivision is that in the interpolatory case only one

type of subdivision rule is necessary: a positioning rule for new vertices on faces

k−1

. In the uniform case, this rule can easily be derived so as to reproduce

polynomials. Figure 7.30 shows the face rules for a quad and a triangle scheme,

respectively. These rules are chosen so as to reproduce cubic functions for the quad

rule and quadratic functions for the triangle rule. Note that the support of the rule

for triangle meshes is smaller than the Butterfly rule.

A preliminary analysis of the quad scheme (included in the associated Mathe-

matica implementation (

)) shows that the scheme converges to C

limit surfaces

for uniform meshes and produces smooth limit surfaces at extraordinary vertices

for a small range of valences. For the triangle rules, we have no estimates of the

smoothness of the resulting surfaces and leave the analysis of this scheme to the

interested reader. In both cases, we suspect that it will be necessary to develop

variants of these rules to produce schemes that are

for all valences.

7.4.2 Dual Subdivision Schemes

In section 5.3.2, we observed that the uniform B-splines of odd order had the

property that the control points in

could be viewed as being positioned at

Z], the midpoints of the intervals defined by the grid

Z. Such spline schemes

7.4 Other Types of Polyhedral Schemes 235

(a) (b)

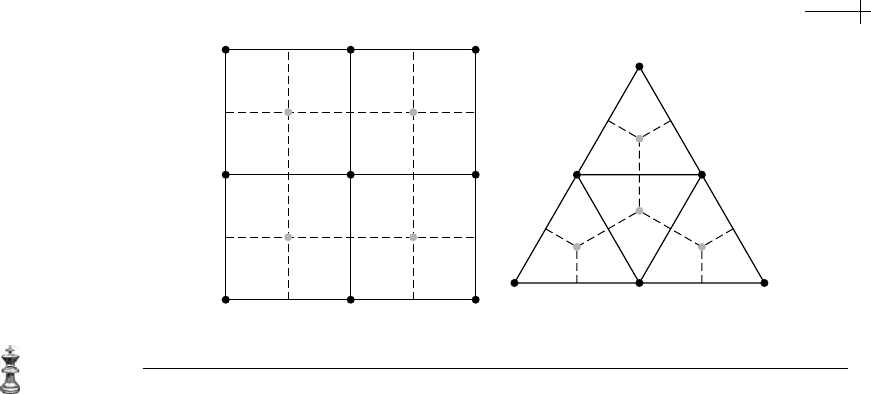
Figure 7.31 Dual meshes (dotted) for quad (a) and triangle (b) meshes.

were referred to as dual schemes. Now, a surface scheme is a dual scheme if the

control points in the vector

p are attached to the faces of the surface mesh M. Note

that placing these control points on the faces of

M defines a new topological surface

mesh

D[M] whose vertices correspond to the faces of M, whose faces correspond

to vertices of

M, and whose edges connect two vertices in D[M] if and only if the

associated faces in

M share a common edge. This surface mesh D[M] is the topological

dual of a surface mesh

Figure 7.31 shows a plot of the topological duals of a portion of a uniform

quad mesh and a portion of a uniform triangle mesh. These duals (dotted lines)

are, respectively, another quad mesh and a hexagonal mesh. Note that constructing

the dual of

M “flips” the edges of M in constructing D[M]. One important feature

of the topological dual is that for closed surface meshes the dual of the dual of a

mesh yields the original mesh (i.e.,

D[D[M]] == M). For example, the dual of the

topological mesh for a cube is the mesh of an octahedron. Likewise, the dual of

the topological mesh for an octahedron is a topological cube.

Now, given a primal subdivision scheme that maps a coarse mesh

k−1

to a

refined mesh

, the corresponding dual scheme maps the coarse mesh D[M

k−1

]

to the refined mesh D[M

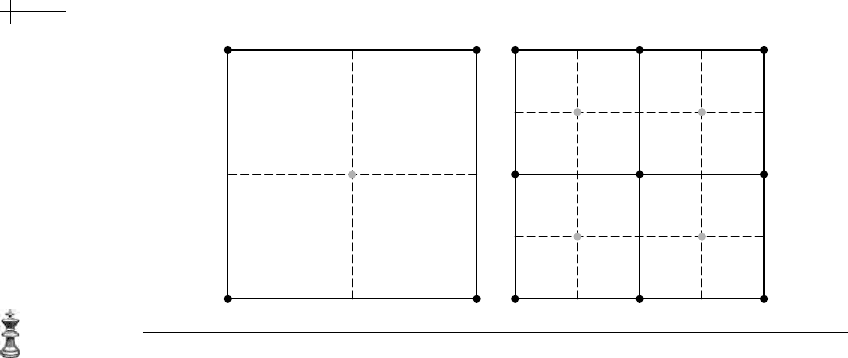
]. Figure 7.32 shows an example of dual topological sub-

division applied to a quad mesh. The solid lines are the meshes

k−1

and M

respectively. The dotted lines are the dual meshes

D[M

k−1

] and D[M

], respectively.

Note that the vertices of

D[M

k−1

] are not a subset of the vertices of D[M

], as they

were for the previous primal schemes. Luckily, dual subdivision retains the key

236 CHAPTER 7 Averaging Schemes for Polyhedral Meshes

Figure 7.32 Topological subdivision of a dual quad mesh.

property that made primal subdivision work: isolation of extraordinary features.

In the primal case, topological subdivision introduces only ordinary vertices and

isolates existing extraordinary vertices. In the dual case, topological subdivision in-

troduces only ordinary faces and isolates those extraordinary faces that are dual to

extraordinary vertices in

The simplest example of a dual subdivision scheme is constant subdivision. This

scheme takes an existing mesh

k−1

, p

k−1

} and splits each face f of M

k−1

into four

subfaces in

. Given the control point in p

k−1

corresponding to this face f , we next

make four copies of this control point for the four subfaces of

f . Unfortunately, this

scheme is not particularly interesting for parametric meshes because the scheme

converges to a set of points corresponding to those in the original vector

. (In the

functional case, this scheme converges to piecewise constant functions; hence the

name.)

The main application of constant subdivision lies in serving as a preprocessor

for higher-order dual schemes. The method for generating these schemes is the

same as in the primal case: apply an appropriate averaging operator to the results

of some type of simple subdivision operation. For primal meshes, applying quad

averaging to the result of linear subdivision leads to smooth primal schemes. For

dual meshes, applying quad averaging to the result of constant subdivision leads to

smooth dual schemes.

For example, one round of quad averaging leads to a dual scheme that

generalizes biquadratic B-splines to polyhedral meshes. The left-hand portion of

Figure 7.33 shows the subdivision rule for this scheme at an extraordinary vertex

v of valence n in M

k−1

. The dark lines bound the face in D[M

k−1

] dual to v; the

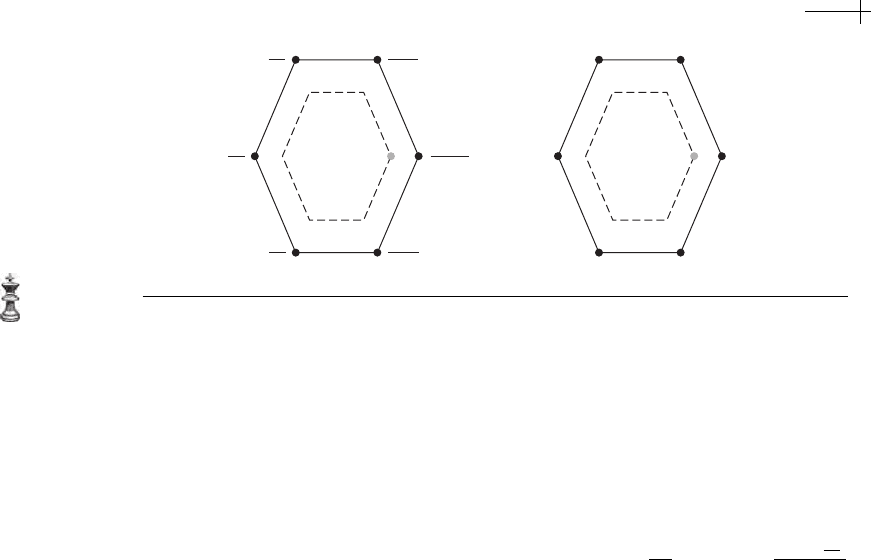
7.4 Other Types of Polyhedral Schemes 237

2  n

1  2n

w[2]

w[...]

w[n  2] w[n  1]

w[1]

w[0]

2  n

Figure 7.33 Two subdivision rules for a dual quad scheme at an extraordinary vertex.

dashed lines bound the face in D[M

] dual to v. The position of a vertex (gray dot)

D[M

] is expressed as a weighted combination of the vertices of D[M

k−1

] (black

dots), as shown. This subdivision rule defines a dual scheme that converges to

smooth limit surfaces even in the presence of extraordinary vertices.

This subdivision rule was first proposed by Doo and Sabin in their original

paper [45]. Doo and Sabin also propose an alternate subdivision rule shown on the

right in Figure 7.33. The weights

w[i ] have the form w[0] =

n+5

and w[i ] =

3+2 Cos[

2i π

]

for i == 1...n − 1. This alternate rule also produces limit surfaces that are smooth

everywhere.

Higher-order dual schemes can be constructed by applying several rounds of

quad averaging. For example, Zorin and Schr

oder [170] generate a dual quar-

tic subdivision scheme via constant subdivision, followed by two rounds of quad

averaging.

Dual schemes based on other types of topological splits are also possible. For

example, Peters and Reif [115] devised a scheme that they refer to as the “mid-

edge” scheme. Topologically, this scheme is the dual of the face-splitting scheme

for quads described previously; that is, vertices in

are placed at the midpoints of

edges in

k−1

. On uniform grids, two rounds of the mid-edge scheme correspond

to one round of subdivision for the four-direction quadratic box spline. Peters and

Reif show that their scheme is

even in the presence of extraordinary vertices.

Habib and Warren [70] describe another variant of the quadratic box spline rule

that converges to a

surface at extraordinary vertices and allows more precise

control over boundary behavior.

Dual schemes based on triangle subdivision of

k−1

are also possible (although

rarely used in practice). These schemes lead to primal subdivision schemes on the

238 CHAPTER 7 Averaging Schemes for Polyhedral Meshes

hexagonal mesh D[M

k−1

]. For example, Goodman [68] describes a construction for

what he refers to as a “cubic half-boxspline.” This spline is a dual spline defined

on a three-direction triangle mesh. The subdivision scheme for this spline is, there-

fore, a primal subdivision scheme for hexagonal meshes. The authors leave the

details of deriving the actual subdivision rules for this scheme to the interested

reader.

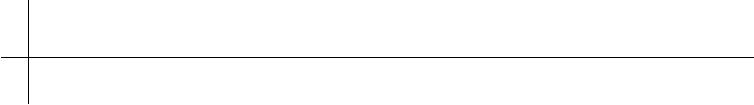
CHAPTER 8

Spectral Analysis at an

Extraordinary Vertex

Given a polyhedral mesh {M

k−1

, p

k−1

}, the subdivision schemes considered in Chap-

ter 7 consisted of two major steps: topological subdivision and geometric posi-

tioning. For most schemes, topological subdivision consisted of splitting each face

k−1

into four new subfaces to produce a new topological mesh M

. Geo-

metric updating involved positioning new vertices

via the subdivision relation

= S

k−1

. For these schemes, the choice of the subdivision rules used in S

k−1

depended only on the topology of M

k−1

, not on the level k. Such schemes in which

the same subdivision rules are used at all levels of subdivision are stationary subdi-

vision schemes. Note that the scheme for surfaces of revolution was not stationary,

because the tensions

, ρ

used in constructing S

k−1

varied as a function of

The goal of this chapter is to develop a set of tools for analyzing the behavior

of stationary subdivision schemes at extraordinary vertices. The first part of the

chapter introduces the main tool used in understanding the behavior of a subdi-

vision process at an extraordinary vertex: spectral analysis. The second portion of

the chapter uses spectral analysis to derive necessary and sufficient conditions for

stationary subdivision schemes to produce smooth limit surfaces. The third portion

of the chapter applies these analysis techniques to an example problem, Loop’s

subdivision scheme, and shows that this scheme converges to a smooth limit sur-

face at extraordinary vertices. Finally, we conclude the book with a brief overview

of some current areas of research in subdivision.

8.1 Convergence Analysis at an Extraordinary Vertex

The averaging schemes of Chapter 7 generalized uniform subdivision schemes to

arbitrary polyhedral meshes. The key idea behind these schemes was to apply

uniform subdivision within each triangle or quad of the original mesh

. Because

239

240 CHAPTER 8 Spectral Analysis at an Extraordinary Vertex

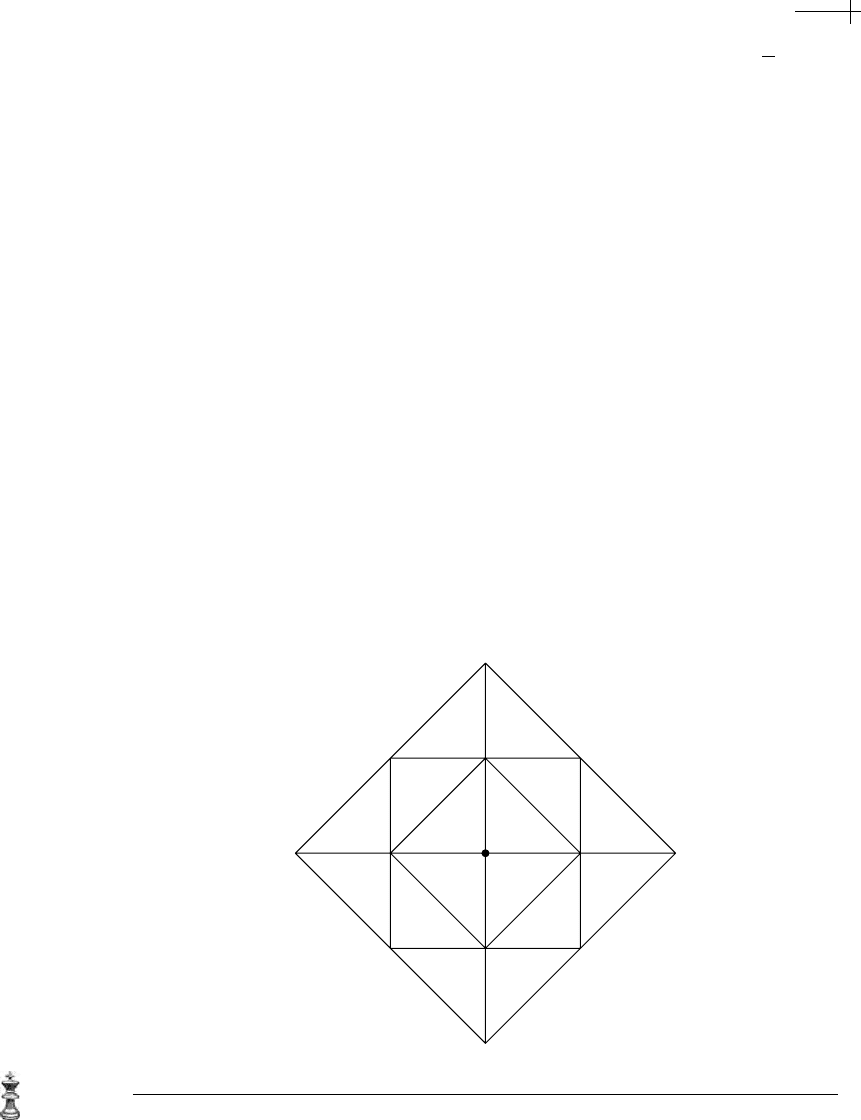
Figure 8.1 Triangular and quadrilateral meshes M consisting of a single extraordinary vertex.

the only nonuniformities present in the resulting meshes M

are those that are

inherited from the original mesh

, these nonuniformities (the extraordinary ver-

tices) are isolated inside an otherwise uniform mesh. Our approach in the next two

sections is to analyze the behavior of averaging schemes on a mesh

M consisting of a

single extraordinary vertex of valence

n surrounded by an otherwise uniform mesh.

In the two-dimensional case, such meshes

M can be formed by combining

several copies of a quadrant of the uniform mesh

. These sectors correspond to

the mesh

)

where Z

denotes the grid of non-negative integers. If M consists

of a single extraordinary vertex

v of valence n, M can be formed by joining n sectors

around a common, extraordinary vertex

v of valence n. Figure 8.1 shows several

examples of such triangular and quadrilateral meshes for an extraordinary vertex

of valence three to eight. (Only a finite portion of the infinite mesh

M centered

around the extraordinary vertex

v is shown.)

These infinite meshes

M have the nice property that they are invariant under

repeated topological subdivision; that is, if

== M, then M

== M for all k ≥ 0.

In other words, topologically subdividing such a mesh

M always returns M back.

Because the subdivision matrices

are functions of the topology M

, the subdivi-

sion process for such an initial mesh

M is independent of the level of subdivision. In

particular, if

S is the bi-infinite subdivision matrix associated with M, the geometric

update rule for the mesh

M has the form

= Sp

k−1

, (8.1)

where p

is the vector of initial vertex positions.

8.1.1 The Limit Surface at an Extraordinary Vertex

Chapter 3 discussed developing tools for analyzing the behavior of subdivision

schemes defined over uniform meshes. The key observation there was to define a

8.1 Convergence Analysis at an Extraordinary Vertex 241

function p

[x, y] associated with a vector of coefficients p

on the grid

and

then to consider the convergence of this sequence of functions. In our current case,

we wish to analyze the behavior of this vector

when associated with the mesh

M. Because M consists of n sectors, we can number the vertices of p

using a triple

index

{h, i, j }, where h denotes a sector of M and {i, j } denotes a particular vertex in

that sector where

i, j ≥ 0

. To model the connection between sectors, this indexing

is also subject to the following rules:

■

The indices {h, 0, 0} coincide with the extraordinary vertex v for 0 ≤ h < n.

■

The boundary vertices of each sector overlap subject to the indexing rules

{h, 0, i } == {mod [h + 1, n], i, 0} for 0 ≤ h < n.

Figure 8.2 shows an example of this indexing for an extraordinary vertex of valence

four in a triangular mesh.

Given a vector of coefficients

,weletp

[[ h , i, j]] denote the coefficient in p

with index {h, i, j }. Based on this indexing, we now define n associated piecewise

polynomial functions

[h, x, y]

for 0 ≤ h < n. For triangular meshes, these functions

[h, x, y] are typically piecewise linear over each sector of M, whereas in the quad

case the functions are piecewise bilinear over each sector of

M. In both cases, these

000

020

120

220

320

010

011

110

111

210

211

310

311

Figure 8.2 An example of vertex indexing for the two-ring of an extraordinary vertex of valence four.

242 CHAPTER 8 Spectral Analysis at an Extraordinary Vertex

functions interpolate the values of p

in a manner similar to that of the uniform

case; that is,





= p

[[ h , i, j]]. (8.2)

Due to the compatibility conditions associated with this indexing, these func-

tions coincide along the common boundary shared by two adjacent sectors; that

is, they satisfy

[h, 0, x] == p

[mod[h + 1, n], x, 0] for 0 ≤ h < n and x ≥ 0. Given a

subdivision process of the form

= S

, we define the limit surface associated

with this process to be the parametric surface of the form

∞

[h, x, y] = lim

k→∞

[h, x, y], (8.3)

where 0 ≤ h < n and x, y ≥ 0. As we shall see, the existence of this limit surface

∞

[h, x, y]

depends on the structure of the subdivision matrix S. Away from the

extraordinary vertex

v, the subdivision rules in S are typically chosen to reproduce

a uniform subdivision scheme. Because the mesh

M is uniform except at v, the limit

surface

∞

[h, x, y] shares all of the convergence and smoothness properties of the

uniform scheme everywhere except at the extraordinary vertex

v (with coordinates

{x, y} == {0, 0}). All that remains is to analyze the behavior of this surface at v.

To illustrate the concepts discussed in this chapter, we will consider a single

running example throughout the entire chapter. The subdivision scheme for this

example is the univariate stationary scheme associated with the following bi-infinite

subdivision matrix

S =

⎛

⎜

⎝

.... . . . ....

. 0

00000.

. 00

00000.

. 00

0000.

. 000

0000.

. 000

000.

. 000 0

000.

. 000 0

00.

. 000 0 0

00.

. 000 0 0

0 .

.... . . . ....

⎞

⎟

⎠

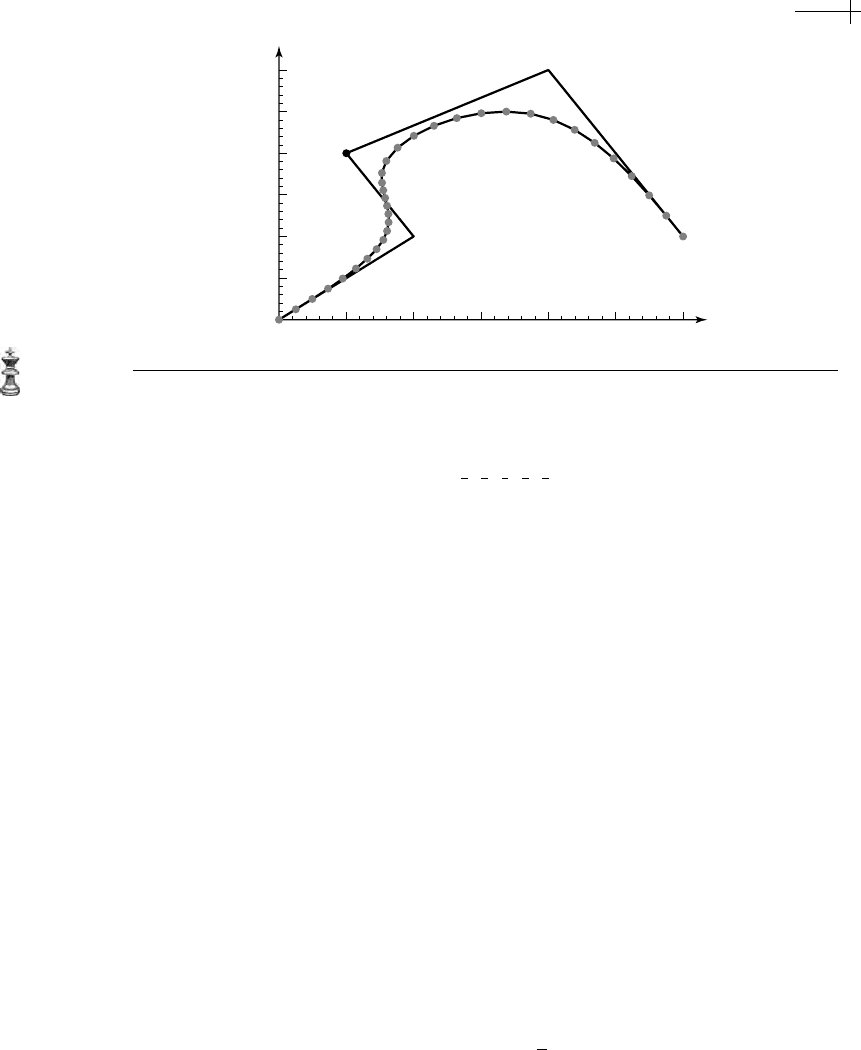
8.1 Convergence Analysis at an Extraordinary Vertex 243

Figure 8.3 Three rounds of subdivision with a nonuniform curve scheme.

This matrix has three nonuniform columns, with the remaining columns corre-

sponding to the subdivision mask

{

} for a uniform cubic B-spline.

Figure 8.3 shows several rounds of subdivision applied to an initial control polygon.

The large, dark vertex on

is the extraordinary vertex v.

Our approach for this univariate example is to treat the central vertex

v as

an extraordinary vertex joining two sectors (each a uniform mesh

). The three

special columns of

S arise from the need to form a smooth transition between these

two meshes. Following our indexing scheme for surfaces, entries of vectors

asso-

ciated with this scheme can be indexed by a pair of the form

{h, i }, where h == 0, 1

and i is a non-negative integer. Index h == 0 corresponds to the upper-left-hand por-

tion of the vector

, whereas indices with h ==

1 correspond to lower-right-hand

portions of the vector

. Enumerated in order, these indices have the form

{..., {0, 2}, {0, 1}, {0, 0} == {1, 0}, {1, 1}, {1, 2}, ...}.

Our task in the rest of this section and the next two is to analyze the convergence

and smoothness of the composite parametric limit curve

∞

[h, x] defined via a

univariate version of equation 8.3.

8.1.2 Local Spectral Analysis

The key to analyzing the behavior of the limit surface p

∞

[h, x, y] near an extraordi-

nary vertex

v is to construct a finite submatrix S of the infinite subdivision matrix

S that encapsulates the behavior of the scheme near the extraordinary vertex v.In