Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach

Подождите немного. Документ загружается.

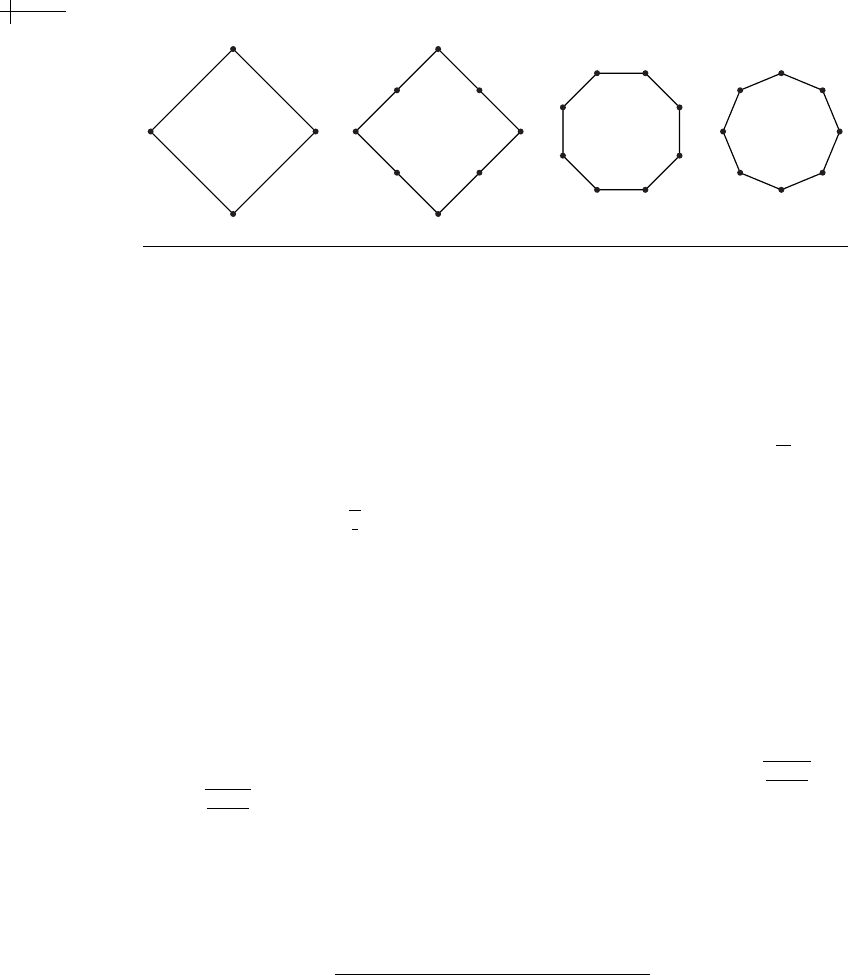
214 CHAPTER 7 Averaging Schemes for Polyhedral Meshes

Figure 7.13 The three separate transformations comprising a single round of subdivision.

Finally, the second round of averaging places the vertices of p

at the midpoints of

these weighted averages.

For example, Figure 7.13 shows the three separate transformations of equa-

tion 7.4 used to perform a single round of subdivision applied to a diamond. The

leftmost polygon

is a diamond whose initial tension is σ

= Cos[

2π

] == 0.

The polygon immediately to its right, 

, is the result of applying linear subdi-

vision. The next polygon (a regular octagon) is the result of weighted averaging

using the tension

)

. Note that applying midpoint averaging here (i.e., σ

== 1)

would not produce a regular octagon. The rightmost polygon,

, is another regular

octagon that results from a final round of averaging using midpoints.

The beauty of this reformulated curve scheme is that it has a simple gen-

eralization to quad meshes. For each quad in the initial mesh

, we assign two

tension parameters,

and ρ

, one per pair of parallel edges in the quad. Each round

of subdivision takes a coarse polyhedron

k−1

, p

k−1

}; applies bilinear subdivision

to produce a finer, intermediate mesh

, p

}; and then applies weighted quad

averaging to produce the final polyhedral mesh

, p

}. During bilinear subdivi-

sion, the tensions

k−1

and ρ

k−1

for a given quad are updated via σ

)

1+σ

k−1

and

)

1+ρ

k−1

. These new tensions are then assigned to the appropriate pairs of edges

for each of the four quad subfaces. These new tensions are then used to compute

weighted centroids of each quad during the averaging phase. Given a quad

{v, u, t, s}

in M

, this weighted centroid is the tensor product of the univariate weighting rule

and has the form

(σ

p

[[v]] + p

[[ u ]] ) + (σ

p

[[ t ]] + p

[[ s ]] )

(σ

+ 1)(ρ

+ 1)

(7.5)

where v is a vertex of M

k−1

, s lies on a face of M

k−1

, and u and t lie on edges of

k−1

tagged by ρ

and σ

, respectively. (The necessary orientation information for

this rule can be maintained for each quad by storing its topological indices in a

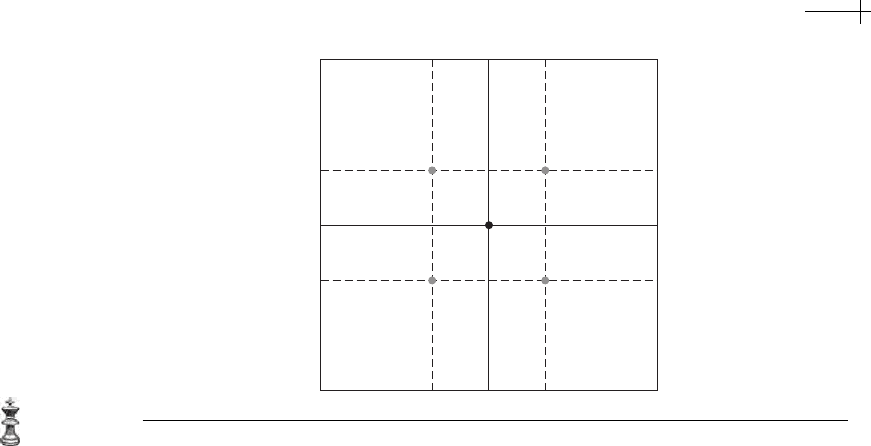
7.2 Smooth Subdivision for Quad Meshes 215

␳

␴

␳

␴

Figure 7.14 Computing the weighted average of the vertices on the solid grid. Gray vertices are interme-

diate points used in computing the position of the black vertex.

systematic order.) The second round of averaging is done by computing the centroid

of these weighted centroids. The update rule for these two rounds of averaging is

exactly that of equation 7.2, in which

cent is the weighted centroid of equation 7.5.

Figure 7.14 illustrates weighted quad averaging in action. The solid lines denote

the mesh

, p

} produced by bilinear subdivision. To compute the new vertex po-

sition of the central black vertex, weighted quad averaging computes the weighted

gray centroids for each quad in

. Note that the weight σ

is always attached to

the vertex of the quad that is also a vertex of

k−1

. Finally, the central black vertex

is repositioned at the centroid of the gray vertices.

This subdivision scheme has several remarkable properties. Because the ini-

tial tensions

and ρ

are greater than or equal to −1, the scheme involves only

convex combinations of control points. If all initial tensions are chosen to be

the scheme reduces to bilinear subdivision plus unweighted averaging. For tensor

product meshes with a single global tension for each coordinate, the resulting limit

surfaces are the tensor product of two

curve schemes. Consequently, the surfaces

must be

. For tensor product meshes whose associated tensions are not the ten-

sor of two sets of curve tensions, the scheme is no longer necessarily

. However,

numerical tests show that the limit surfaces still appear to be

. At extraordinary

vertices, the limit surfaces remain

. The smoothness of this scheme is analyzed

in greater detail in Morin et al. [107].

216 CHAPTER 7 Averaging Schemes for Polyhedral Meshes

To complete this section, we describe a simple construction for generating

surface meshes whose limit surfaces are surfaces of revolution. Given a control

polygon

(and a list of tensions for its segments) in the xz plane, we construct a

tensor product surface mesh

(and associated set of tensions) in xyz space whose

limit

∞

is the surface formed by revolving p

∞

around the z axis. We construct s

making

m copies of p

and revolving the i th copy around the

z axis by

2πi

radians.

If we decompose

into its components in x and z (i.e., p

={p

, p

}), the ith copy

has the form



Cos



2πi



, Sin



2πi



, p

Joining these m revolved curves (and their tensions) yields a tensor product mesh.

If the tensions in the direction of revolution for this mesh are initialized to

Cos[

2π

cross sections of the associated limit surface

∞

taken orthogonal to the z axis are

circles (i.e.,

∞

is a surface revolution).

However, as observed in section 4.4, this limit surface

∞

is not the surface

of revolution formed by revolving

∞

around the z axis. Due to the averaging

that takes place between adjacent revolved copies of

, s

∞

is “squeezed” toward

the

z axis. To counteract this effect, we must scale the x and y coordinates of the

initial polyhedron

by a factor of

2π

Csc [

2π

] (see [107] for a derivation of this

constant). For

m ≥ 4, this scaled version of s

has the property that s

∞

is the surface

of revolution formed by revolving the limit curve

∞

around the z axis.

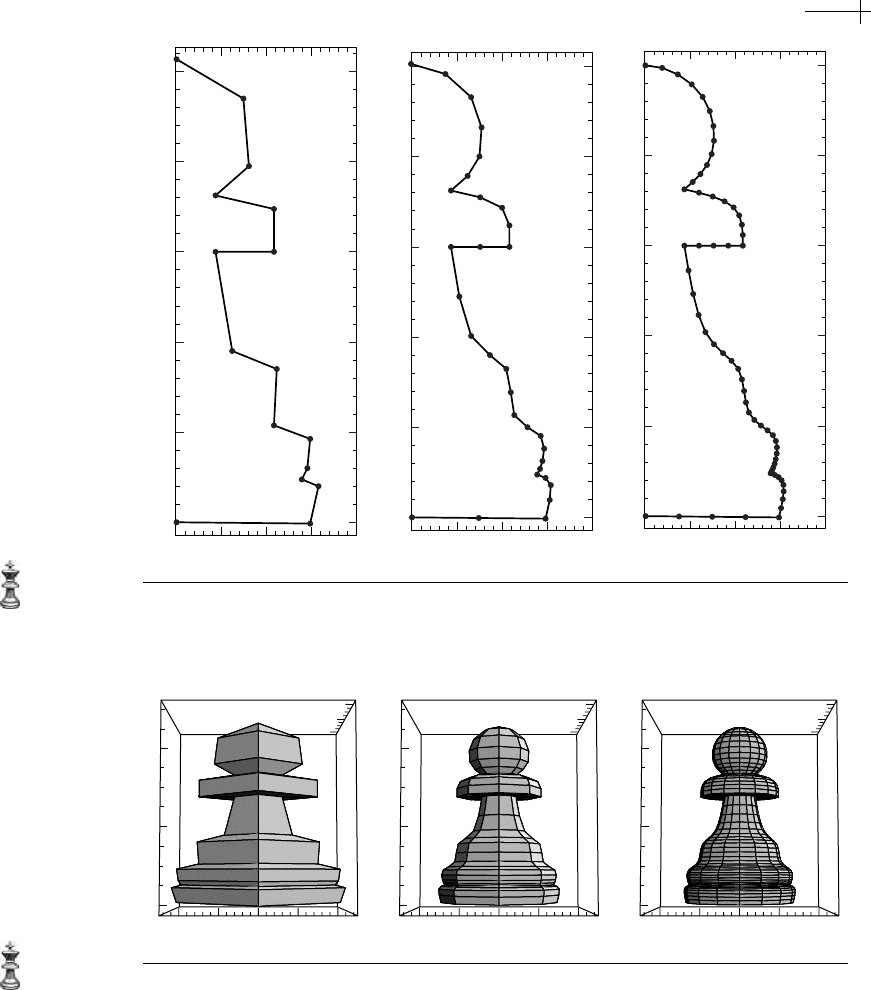
Figures 7.15 and 7.16 show an example of this process used to construct a

pawn. The leftmost polygon in Figure 7.15 is the control polygon

. The polygons

to its right are refined polygons

and p

. The leftmost surface in Figure 7.16 is the

scaled tensor product surface mesh

formed by revolving p

around the vertical

z axis. Note that a vertical cross section of s

is “fatter” than p

due to the scaling in

the

x direction by

2π

Csc [

2π

]. Subsequent meshes s

and s

appearing to the right are

the result of subdivision using weighted averaging. Note that vertical cross sections

of these meshes

are converging to p

. (This example also revolves crease vertices

to introduce crease edges on the limit surface s

∞

. See the next section for

details on creating crease vertices and crease edges.)

Figures 7.17 and 7.18 show two other examples of simple surfaces of revolu-

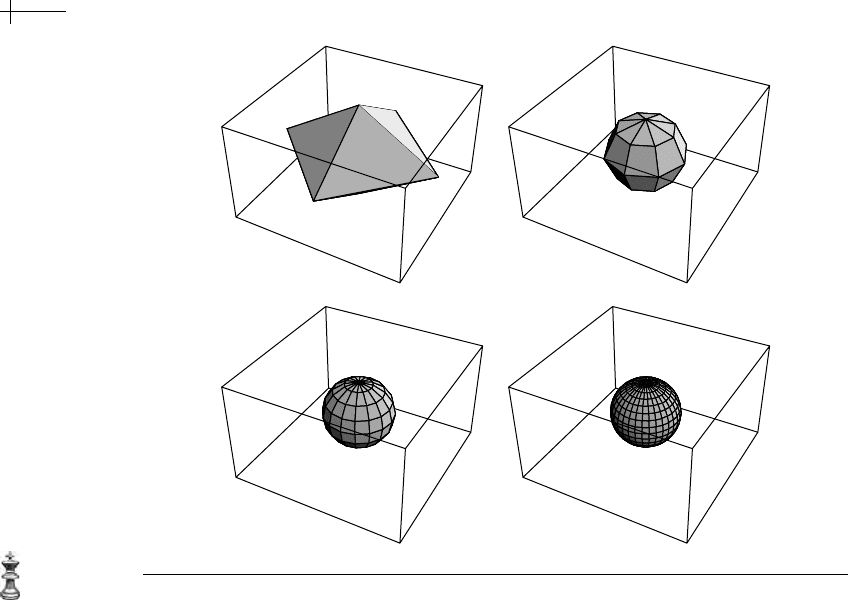
tion. Figure 7.17 shows an octahedron being subdivided into a sphere. Figure 7.18

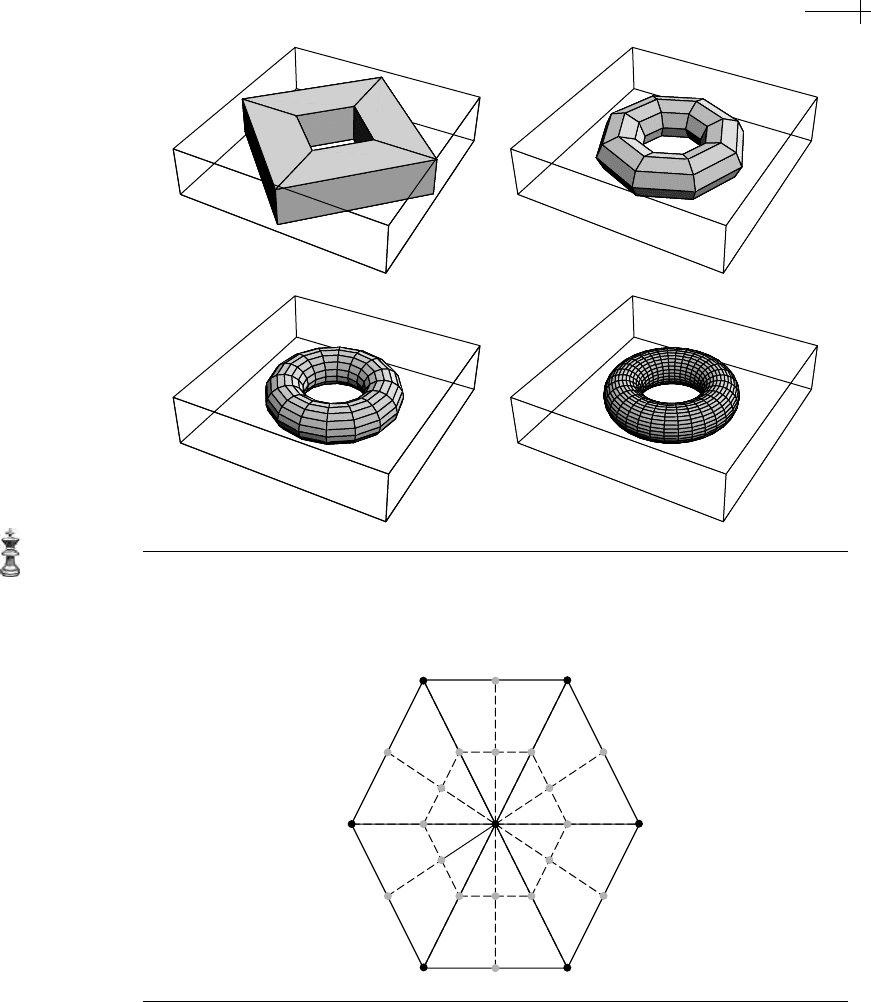
shows a torus being created through subdivision. In both cases, the original profile

curves

∞

were circles. In the case of the torus, the profile curve does not intersect

the

z axis, and thus the surface of revolution is a smooth, single-sheeted surface.

7.2 Smooth Subdivision for Quad Meshes 217

0 .5 1 1.5 2

Figure 7.15 Subdivision of the proﬁle curve for a pawn.

2 1

2

Figure 7.16 A pawn created by subdividing the revolved proﬁle curve.

218 CHAPTER 7 Averaging Schemes for Polyhedral Meshes

Figure 7.17 Three rounds of subdivision converging to a sphere.

In the case of the sphere, the profile curve is a circle symmetrically positioned on

the

z axis. Due to this positioning, the resulting surface of revolution is a smooth,

double-sheeted surface (i.e., a surface that consists of two copies of the same sur-

face). More generally, revolving any profile curve that is symmetric with respect to

the

z axis through 2π radians results in a double-sheeted surface.

In practice, we wish to avoid this double-sheetedness when the profile curve

∞

is symmetric with respect to the z axis. The solution to this problem is to revolve

the initial symmetric polygon

through only π radians. Because the polygon p

symmetric with respect to the

z axis, the new polyhedron s

is closed (and single-

sheeted). If the intersection of the

z axis and polygon p

occurs at vertices of p

, this

quad mesh

has poles at these vertices. These poles consist of a ring of degenerate

quads (triangles) surrounding the pole (as shown by the dark lines in Figure 7.19).

Applying bilinear subdivision plus weighted averaging to this single-sheet poly-

hedron

yields a single-sheeted surface of revolution s

∞

that agrees with the

double-sheeted surface of revolution produced by revolving

through 2π radians.

The key to this observation is to note that applying this subdivision scheme to

7.2 Smooth Subdivision for Quad Meshes 219

Figure 7.18 Three rounds of subdivision converging to a torus.

Figure 7.19 Subdividing a degenerate quad mesh around a pole.

220 CHAPTER 7 Averaging Schemes for Polyhedral Meshes

both the single-sheeted and double-sheeted variants of s

yields the same surface

(single-sheeted and double-sheeted, respectively) as long as the degenerate quads

at the poles of the single-sheet version are treated as such and are subdivided as

shown in Figure 7.19 (the dotted lines).

7.2.4 Averaging for Quad Meshes with Embedded Creases

Up to now, we have focused on constructing subdivision schemes that yield smooth

limit surfaces everywhere. However, most real-world objects have boundaries and

internal creases where the surface of the object is not smooth. Our goal in this

section is to modify the averaging rules developed in the previous two sections to

allow for the controlled introduction of “crease” curves and vertices onto the limit

surface. The key to this modification is to restrict the application of the averaging

rules to a subset of the mesh

corresponding to the crease curves and vertices.

To model such features, the topological base mesh

associated with the

scheme is expanded to allow the inclusion of vertices and edges, as well as faces. For

example, the base mesh

for a quadrilateral surface may contain line segments

and vertices, as well as quad faces. These lower-dimensional cells define crease

curves and crease vertices in the resulting surface mesh. For example, the initial

topology

for the bounded quad surface patch of Figure 7.20 consists of four

faces, eight boundary edges, and four corner vertices. If the vertices in this

3 × 3

grid are numbered



123

456

789



, the initial topology

is a list of the form

{{1, 2, 5, 4}, {4, 5, 8, 7}, {2, 3, 6, 5}, {5, 6, 9, 8}, (7.6)

{1, 4}, {4, 7}, {1, 2}, {2, 3}, {3, 6}, {6, 9}, {7, 8}, {8, 9},

{1}, {3}, {7}, {9}}.

Figure 7.20 Bilinear subdivision plus averaging for a surface patch with boundary creases.

7.2 Smooth Subdivision for Quad Meshes 221

Given this new representation, bilinear subdivision is performed as usual, with

each quad split into four quads, each edge split into two edges, and each vertex

copied.

Given the mesh

produced by bilinear subdivision, we define the dimension

dim[v] of a vertex v in M

to be the dimension of the lowest-dimensional cell in M

that contains v. In the previous example,

dim[v] has the values

v :123456789

dim[v]:010121010

Having computed dim[v] for M

, the rule for quad averaging at vertex v is modified

to use only those cells whose dimension is

dim[v]. In particular, the update process

of equation 7.2 is adjusted as follows:

Quad averaging with creases: Given a vertex

v, compute the centroids of those

cells in

containing v whose dimension equals dim[v]. Reposition v at the centroid

of these centroids.

This modification ensures that the subdivision rules for vertices on a crease are

influenced only by vertices on the crease itself. For example, if

contains a vertex

(a cell of dimension

0), this modified averaging rule leaves the position of the vertex

unchanged and forces the resulting limit surface to interpolate the vertex. If

contains a sequence of edges forming a curve, the resulting limit surface interpolates

the cubic B-spline associated with the control points along the edges.

To implement this modified version of averaging, we compute

dim[v] and val[v]

(now the number of cells of dimension dim[v] containing v) simultaneously during a

first pass through

. Given these two quantities, the averaging rules described in

the previous sections can then be applied. Quad averaging is particularly amenable

to this change because the update rule for the vertices of a cell is independent of

its dimension. Figure 7.20 shows a surface patch produced by bilinear subdivision

plus averaging applied to the example mesh of equation 7.6. The four edges in

force the boundary of the surface patch to interpolate the B-spline curves defined

by the boundary of the initial mesh. Similarly, the four vertices in

force the

limit surface to interpolate the four corners of the initial mesh.

Figures 7.21 and 7.22 show high-resolution renderings of two more complex

objects, a ring and an axe, during subdivision. The ring includes a crease curve

where the stone meets the ring and four crease vertices at the corners of the stone.

The axe incorporates crease edges at the top and bottom of its handle, crease edges

along its blade, and crease vertices at its corners. Note that in both examples a

compact polyhedral mesh leads to a nontrivial, realistic model.

222 CHAPTER 7 Averaging Schemes for Polyhedral Meshes

Figure 7.21 A ring modeled using a subdivision surface with creases. (Thanks to Scott Schaefer for his help

with this ﬁgure.)

7.2 Smooth Subdivision for Quad Meshes 223

Figure 7.22 An axe modeled using a subdivision surface with creases. (Thanks to Scott Schaefer for his help

with this ﬁgure.)