Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach
Подождите немного. Документ загружается.

224 CHAPTER 7 Averaging Schemes for Polyhedral Meshes
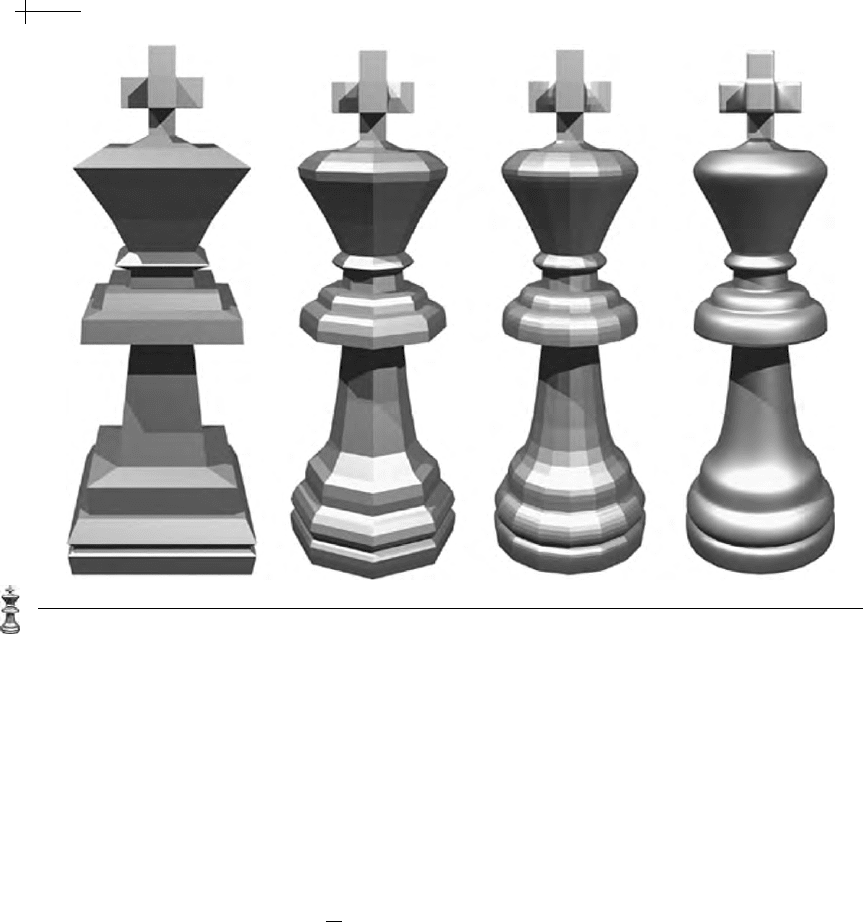
Figure 7.23 A king modeled using weighted subdivision in conjunction with creases. (Thanks to Scott
Schaefer for his help with this figure.)
Using crease vertices and crease edges in conjunction with weighted subdivision
allows us to model complex shapes using coarse initial meshes. Figure 7.23 shows
a high-resolution rendering of another chess piece, a king, during subdivision. This
model was created as a surface of revolution and then hand edited to add the
three-dimensional cross to the king’s head. Figure 7.24 shows a high-resolution
rendering of an umbilic torus defined via subdivision. This object was modeled as
a twisted surface of revolution in which the profile curve, a triangle with concave
edges, was rotated
2π
3
radians around its center during a single sweep around the
axis of revolution. Due to this rotation, the sharp edge on the umbilic torus is
modeled as a single crease curve that wraps around the axis of revolution three
times.
Developing subdivision rules for boundaries and creases of subdivision surfaces
is an active area of research. For example, Hoppe et al. [74] first proposed spe-
cialized rules that allow the introduction of B-spline crease curves onto triangle
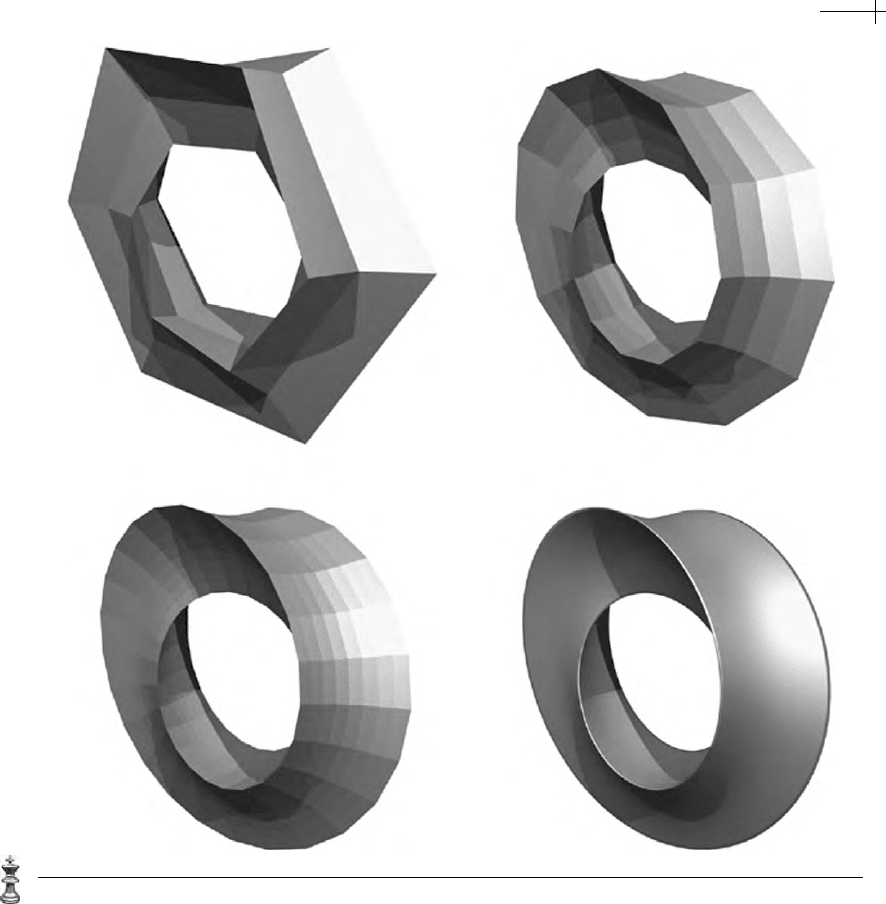
7.2 Smooth Subdivision for Quad Meshes 225
Figure 7.24 An umbilic torus modeled as a twisted surface of revolution with a single crease edge. (Thanks
to Scott Schaefer for his help with this figure.)
subdivision surfaces. Biermann et al. [10] propose an improved set of boundary
rules tailored to deliver better behavior along concave portions of the boundary.
DeRose, Kass, and Truong [42] describe a simple modification to an existing crease
rule that allows the user to control the “sharpness” of a crease. In [94] and [95],
Levin describes a subdivision method called “combined subdivision” that allows for
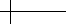
226 CHAPTER 7 Averaging Schemes for Polyhedral Meshes
interpolation of arbitrary curves using subdivision. This scheme is the basis of a
trimming algorithm used to compute the intersection of two subdivision surfaces
[98]. In [109], [110], and [112], Nasri describes several schemes used to interpo-
late points and normals along curves.
7.3 Smooth Subdivision for Triangle Meshes
The previous section described a scheme for smoothly subdividing a quadrilat-
eral mesh in which a single round of subdivision is decomposed into two simpler
steps: bilinear subdivision and quad averaging. One of the major advantages of this
scheme is that almost all of the topological computation takes place during bilinear
subdivision. The only topological information computed during quad averaging is
the valence
val[v] for each vertex v in M
k
. Maintained as an array, val[v] can easily
be computed during a single pass through
M
k
or simply updated during bilinear
subdivision, in that all old vertices in
M
k−1
inherit the same valence and all new ver-
tices introduced into
M
k
have valence four. This decomposition of the subdivision
scheme into two steps is superior to the single-step approach because it avoids the
need to compute or maintain an explicit set of neighbors for each vertex in
M
k−1
.
Our goal in this section is to develop a similar two-step scheme for smoothly
subdividing triangle meshes. Again, the main benefit of this scheme is that it avoids
the need to compute or maintain explicit neighbor information for the meshes
M
k
.
Clearly, the first step of our scheme should be linear subdivision. As described in
section 7.1, linear subdivision can easily be implemented as a single pass through the
triangles of
M
k−1
. All that remains is to construct an averaging method for triangle
meshes that is analogous to quad averaging. Once we have derived this averaging
operator for uniform triangle meshes, an extension to meshes with extraordinary
vertices follows naturally.
7.3.1 Linear Subdivision Plus Triangle Averaging
The key to constructing an averaging rule for triangle meshes is to recall the three-
direction quartic box spline of Chapter 2. This spline is a
C
2
piecewise quartic
function defined over a three-direction triangle mesh. In particular, the set of di-
rection vectors
for this scheme has the form
={{1, 0}, {1, 0}, {0, 1}, {0, 1}, {1, 1}, {1, 1}}.

7.3 Smooth Subdivision for Triangle Meshes 227
Observe that consists of the direction vectors for piecewise linear splines
{{1, 0}, {0, 1}, {1, 1}} repeated twice. Thus, the subdivision scheme for the three-
direction quartic box spline can be expressed as linear subdivision followed by
averaging with the mask corresponding to these three direction vectors. This two-
dimensional averaging mask is of the form
⎛
⎜
⎝
1
8
1
8
0
1
8
1
4
1
8
0
1
8
1
8
⎞
⎟
⎠
.
For quad meshes, we decomposed the averaging mask of equation 7.1 into the
average of four submasks, each supported over one of the four quads meeting at
the vertex. For triangle meshes, we can decompose the averaging mask into six
submasks, each supported over a triangle incident on the vertex:
⎛
⎜
⎝
1
8
1
8
0
1
8
1
4
1
8
0
1
8
1
8
⎞
⎟
⎠
==
1
6
⎛
⎜
⎝
⎛
⎜
⎝
3
8
00
3
8
1
4
0
000
⎞
⎟
⎠
+
⎛
⎜
⎝
3
8
3
8
0
0
1
4
0
000
⎞
⎟
⎠
+
⎛
⎜
⎝
0
3
8
0
0
1
4
3
8
000
⎞
⎟
⎠
(7.7)
+
⎛
⎜
⎝
000
0
1
4
3
8
00
3
8
⎞
⎟
⎠
+
⎛
⎜
⎝
000
0
1
4
0
0
3
8
3
8
⎞
⎟
⎠
+
⎛
⎜
⎝
000
3
8
1
4
0
0
3
8
0
⎞
⎟
⎠
⎞
⎟
⎠
.
This decomposition again suggests a geometric interpretation for this averaging
mask applied at a vertex
v: compute the weighted centroid of each triangle that
contains
v using the weights
1
4
,
3
8
, and
3
8
at v and its two neighbors; then reposition
v at the centroid of these weighted centroids. This generalized averaging opera-
tion, triangle averaging, can now be applied to triangle meshes with vertices of any
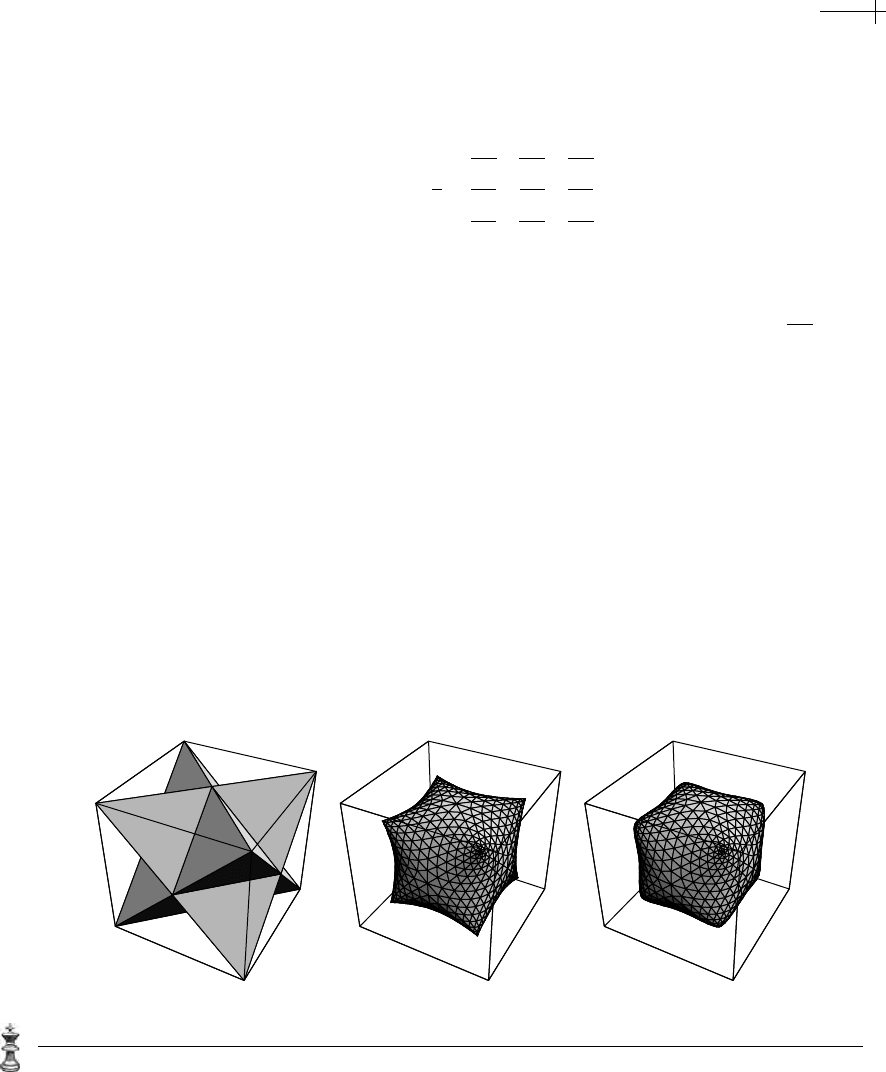
valence. Figure 7.25 shows an example of two rounds of linear subdivision plus
triangle averaging applied to an octahedron. The upper left-hand mesh is the initial
octahedron after linear subdivision. The mesh to its right is the result of applying
triangle averaging to this mesh. The lower left-hand mesh shows the results of ap-
plying linear subdivision to the upper right-hand mesh. The lower right-hand mesh
shows the results of applying triangle averaging to the lower left-hand mesh.
Triangle averaging differs from quad averaging in that the weights used dur-
ing the averaging process vary, depending on which vertex of the triangle is being
updated. Specifically, consider a triangle
{s, t, v} in the triangle mesh {M
k
, p
k
} pro-
duced by linear subdivision. Triangle averaging computes a weighted centroid of
228 CHAPTER 7 Averaging Schemes for Polyhedral Meshes
Figure 7.25 Two rounds of subdivision for an octahedron expressed as alternating steps of linear subdivision
and triangle averaging.
the form
1
4
p
k
[[v]] +
3
8
p
k
[[ s ]] +
3
8
p
k
[[ t ]] when updating the position of vertex v. Simi-
larly, triangle averaging uses weighted centroids of the form
1
4
p
k
[[ s ]] +
3
8
p
k
[[ t ]] +
3
8
p
k
[[v]]
and
1
4
p
k
[[ t ]] +
3
8
p
k
[[ s ]] +
3
8
p
k
[[v]] when updating the position of s and t, respectively.
(Note that using the centroid of the triangle
{s, t, v} in the averaging phase leads to
a subdivision scheme whose limit functions are only
C
1
in the uniform case.)
Luckily, triangle averaging can still be implemented as a single pass through the
topology
M
k
. As for quad averaging, a table of new vertex position p
k
is initialized
to
0, with the positions of the averaged mesh being accumulated on a triangle-
by-triangle basis. The main distinction here from quad averaging is that instead
of computing a single centroid for a triangle
{s, t, v} the three weighted centroids
described previously must be computed and used to update the appropriate vertex
of
{s, t, v}. The update rule for this triangle can be expressed in matrix form as
7.3 Smooth Subdivision for Triangle Meshes 229
the product of an update matrix multiplied by the column vector of old positions
p
k
[[ {s, t, v}]] :
p
k
[[ {s, t, v}]] +=
1
8
⎛
⎜
⎝
2
val[s]
3
val[s]
3
val[s]
3
val[t]
2
val[t]
3
val[t]
3
val[v]
3
val[v]
2
val[v]
⎞
⎟
⎠
p
k
[[ {s, t, v}]] . (7.8)
Here, p
k
[[ {s, t, v}]] is a column vector consisting of the three entries p
k
[[ s ]] , p
k
[[ t ]] , and
p
k
[[v]]. Note that the row of the update matrix corresponding to v sums to
1
val[v]
. This
property is necessary if we desire the corresponding averaging scheme to be affinely
invariant (i.e., the sum of the weights at a vertex is one).
Because triangle averaging is designed to reproduce the averaging rule for three-
direction quartic box splines on valence-six triangle meshes, the resulting limit
surface is
C
2
everywhere except at extraordinary vertices. The next chapter analyzes
the smoothness of the limit surfaces at extraordinary vertices and shows that the
scheme produces limit surfaces that are
C
1
for all valences except three. In this
case, the surface is only
C
0
. The middle portion of Figure 7.26 shows a stellated
octahedron (an octahedron with a regular tetrahedron attached to each face) after
three rounds of subdivision using triangle averaging. Note that the limit surface is
not smooth in the neighborhood of the original valence-three vertices. This problem
is addressed later in this chapter.
(a) (b) (c)
Figure 7.26 A stellated octahedron (a), after three rounds of subdivision with triangle averaging (b) and after
three rounds of subdivision using Loop’s scheme (c).
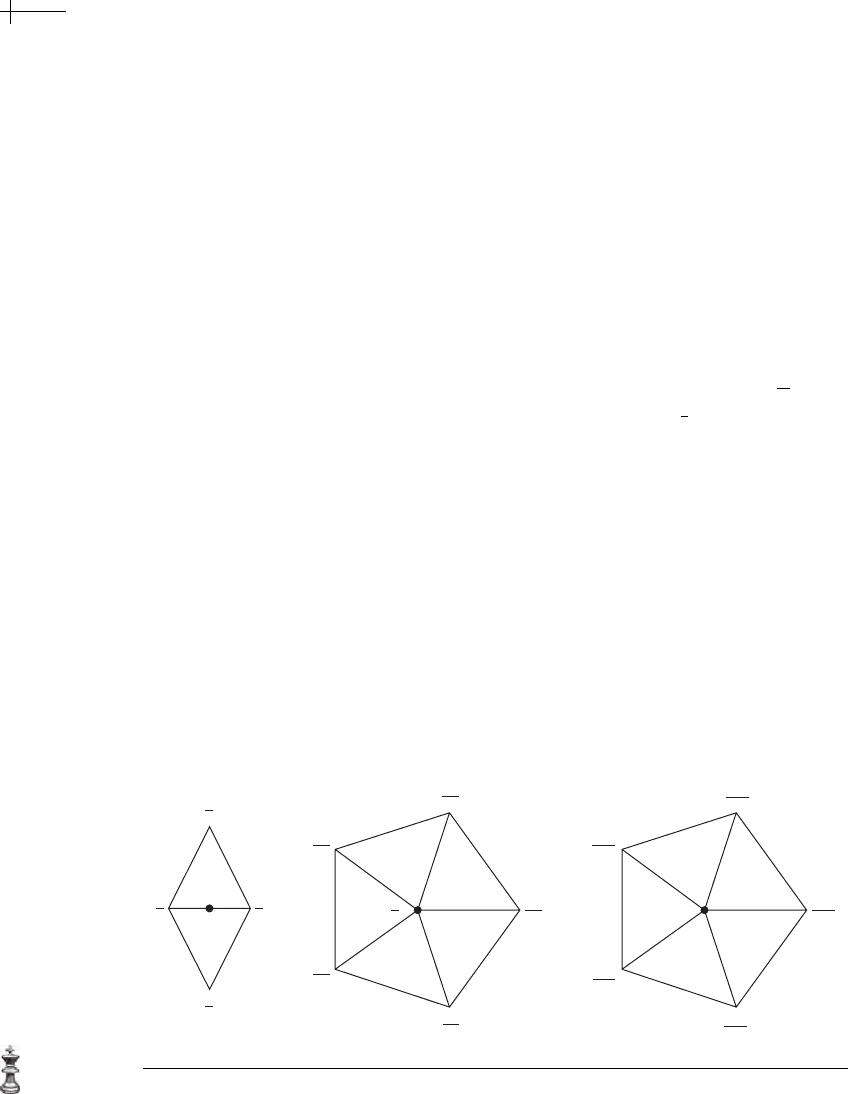
230 CHAPTER 7 Averaging Schemes for Polyhedral Meshes
7.3.2 Comparison to Other Triangle Schemes
The combined action of linear subdivision followed by triangle averaging can be
expressed in a single step as multiplication by a subdivision matrix
S
k−1
. For triangle
schemes, there are essentially two types of rows in
S
k−1
, each corresponding to two
types of subdivision rules. “Edge” rules position vertices of
M
k
that are introduced
during edge splits of
M
k−1
. This rule, the edge rule for the four-direction quartic
box spline, is shown on the left in Figure 7.27.
The remaining type of subdivision rules are “vertex” rules that position those
vertices of
M
k
that are also vertices of M
k−1
. For such a vertex v, the n vertices
adjacent to
v in M
k
lie on the midpoints of n edges incident on v in the origi-
nal mesh
M
k−1
after linear subdivision. Each of these midpoints lies on triangles
containing
v. After triangle averaging, the new position of vertex v is
3
8n
times
the position of each of its
n neighboring vertices in M
k−1
plus
5
8
times the original
position of
v in M
k−1
. The middle portion of Figure 7.27 shows this rule plotted
diagrammatically.
The first smooth subdivision scheme for arbitrary triangle meshes was devel-
oped by Loop in his Master’s thesis [99]. This scheme, also based on a generaliza-
tion of the subdivision rules for the three-direction quartic box spline, converges
to surfaces that smooth at extraordinary vertices of all valences. For example, the
rightmost portion of Figure 7.26 was produced using three rounds of Loop sub-
division. Note that the limit surface is smooth even at extraordinary vertices of
valence three. The rightmost portion of Figure 7.27 shows Loop’s rule for position-
ing an extraordinary vertex of valence
n. The constant w[n] used in this rule has
w[n]
n
w[n]
n
w[n]
n
w[n]
n
1
w[n]
w[n]
n
3
8n
3
8n
3
8n
3
8n
3
8n
5
8
1
8
3
8
1
8
3
8
Figure 7.27 Subdivision rules for smooth triangle schemes.
7.3 Smooth Subdivision for Triangle Meshes 231
the form
w[n] =
5
8
−
3
8
+
1
4
Cos
2π
n
2
. (7.9)
This weight function of equation 7.9, although mysterious looking, was chosen by
Loop so as to make the resulting surfaces close to having continuous curvature (i.e.,
be
C
2
) for low-valence vertices. Although the resulting limit surfaces do not have
continuous curvature (except, of course, at valence-six vertices), the limit surfaces
do have bounded curvature in the neighborhood of extraordinary vertices of valence
three to six (see Peters and Umlauf [117, 118] for details). Both Sabin [135] and
Holt [73] give alternative subdivision rules that also attempt to bound the curvature
of a subdivision surface in the neighborhood of an extraordinary vertex.
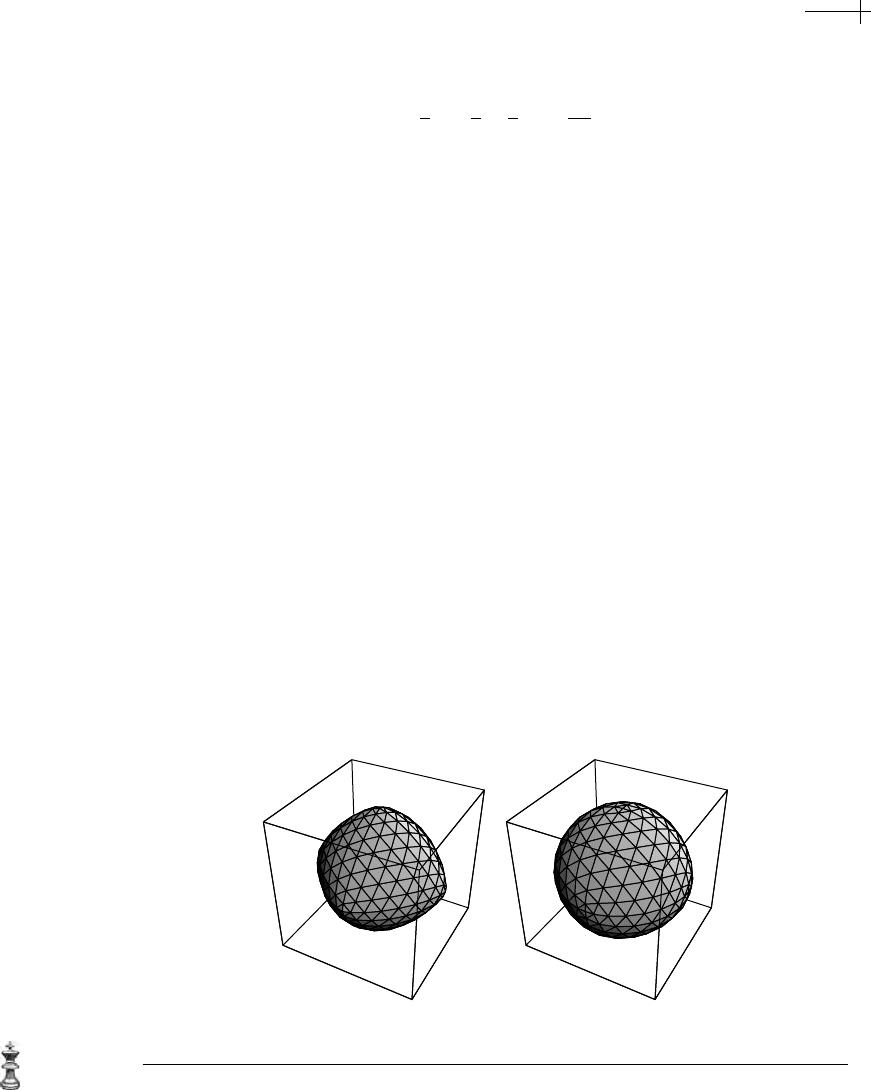
Figure 7.28 shows a side-by-side comparison of linear subdivision with averag-
ing versus Loop’s scheme when the base mesh is an octahedron. The left-hand
surface was produced by linear subdivision plus triangle averaging. The right-
hand surface was produced by Loop’s scheme. Note that the right-hand surface is
“rounder” due to the careful curvature “tuning” of Loop’s subdivision rule. (Section
8.3 provides a more detailed analysis of the differences between these schemes.)
The subdivision rules of Figure 7.27 position a vertex of
M
k
directly in terms
of the positions
p
k−1
of vertices of M
k−1
. Ideally, we would like to recast Loop’s
rule in terms of linear subdivision plus some type of modified averaging with a
simplicity similar to that of triangle averaging. The beauty of the matrix update used
in equation 7.8 is that it can also be modified to reproduce Loop’s extraordinary
(a) (b)
Figure 7.28 A comparison of linear subdivision with triangle averaging (a) versus Loop’s scheme (b).
232 CHAPTER 7 Averaging Schemes for Polyhedral Meshes
vertex rule for triangle meshes. In particular, Loop subdivision can be expressed as
linear subdivision followed by averaging via the matrix update
p
k
[[ {s, t, v}]] +=
⎛
⎜
⎜
⎝
1−2w[val[s]]
val[s]
w[val[s]]
val[s]
w[val[s]]
val[s]
w[val[t]]
val[t]
1−2w[val[t]]
val[t]
w[val[t]]
val[t]
w[val[v]]
val[v]
w[val[v]]
val[v]
1−2w[val[v]]
val[v]
⎞
⎟
⎟
⎠
p
k
[[ {s, t, v}]] ,
where w[n] satisfies equation 7.9. The advantage of this formulation of Loop’s
method is that the positions of vertices in
M
k
can now be accumulated on a
triangle-by-triangle basis as done using triangle averaging.
Although both of the schemes described previously are approximating, inter-
polatory schemes for triangle meshes are also possible. Dyn, Levin, and Gregory
[55] developed the Butterfly scheme, an interpolatory scheme that is
C
1
on three-
direction triangle meshes (see Chapter 3 for details). Although applying the But-
terfly scheme to arbitrary triangle meshes is possible, the resulting surfaces are not
always
C
1
for all possible vertex valences. Zorin et al. [171] describe a modified
version of the Butterfly scheme that is provably
C
1
at extraordinary vertices of all
valences.
7.4 Other Types of Polyhedral Schemes
The previous three sections covered the core subdivision methods for polyhedral
meshes. However, there are a number of other interesting types of subdivision
schemes available for polyhedral meshes. Because subdivision is an active area of
research in which new types of schemes are constantly being invented, it is difficult
to summarize all possible schemes in the subdivision “zoo.” This section provides
a quick overview of some of these schemes, focusing in particular on subdivision
schemes based on other types of topological splits.
7.4.1 Face-splitting Schemes
The two types of topological splits considered previously were based on edge split-
ting. However, these are not the only types of topological splits that can be applied
to a polyhedral mesh. Another interesting class of topological splits involves face-
splitting subdivision. During face-splitting subdivision of a mesh
M
k−1
, new vertices
(gray) are added to
M
k
on the faces of M
k−1
. Existing edges in M
k−1
are then removed
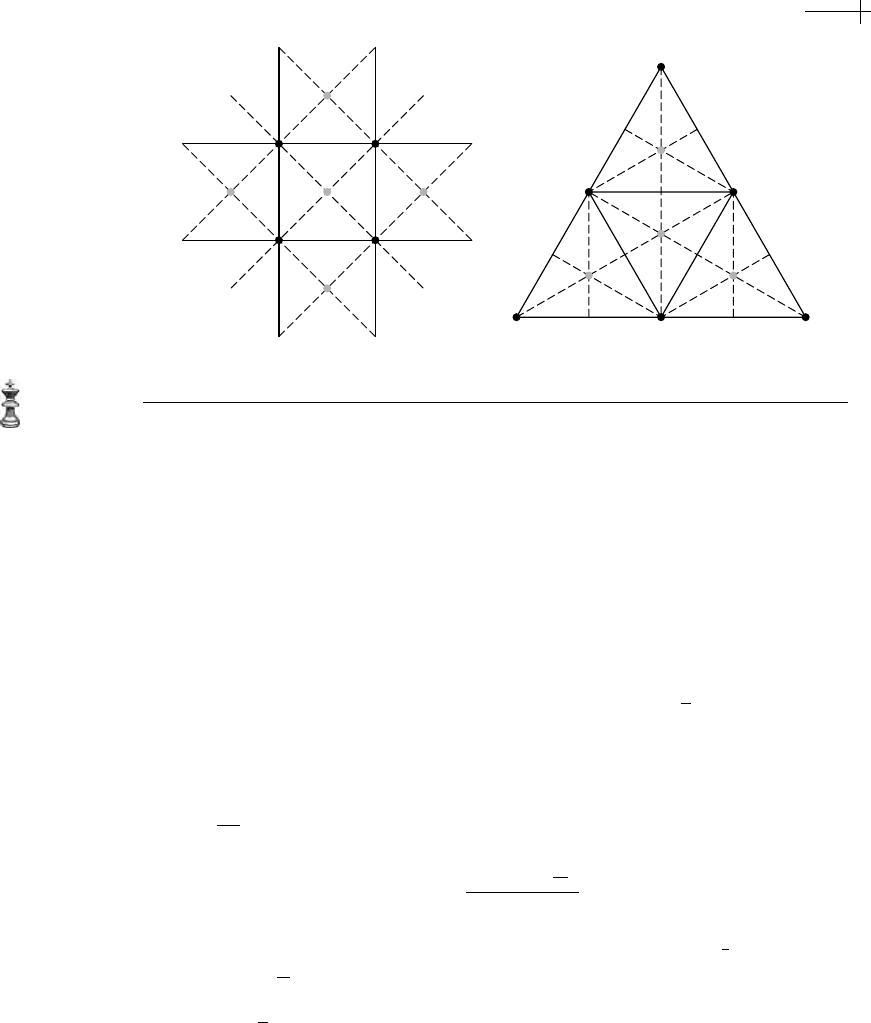
7.4 Other Types of Polyhedral Schemes 233
(a) (b)
Figure 7.29 Face-splitting subdivisions for quad (a) and triangle meshes (b).
with new edges (dashed) added into M
k
, as shown in Figure 7.29. The left-hand
split is for quad meshes, and the right-hand split is for triangle meshes. As in the
case of edge-splitting subdivision, these topological splits introduce only ordinary
vertices and isolate those extraordinary vertices present in the original mesh. An
important feature of these two splits is that performing two rounds of subdivision
is equivalent to one round of binary subdivision for quad meshes and one round of
ternary subdivision for triangle meshes.
Kobbelt [85] has built an interesting subdivision scheme based on face-splitting
subdivision for triangle meshes. This scheme, which he calls
√
3-subdivision, posi-
tions “face” vertices in
M
k
(the gray vertices in Figure 7.29) at the centroid of the
triangular face in
M
k−1
that contains the vertex. The remaining vertices (inherited
from
M
k−1
) are repositioned by applying the weight 1 − w[n] to the vertex and
weights
w[n]
n
to each of its n neighbors where
w[n] =
4 − 2 Cos
&
2π
n
'
9
.
In the ordinary case (i.e., n == 6), this rule leads to a weighting of
2
3
at the vertex
and weights of
1
18
applied to its six neighbors. Kobbelt shows that this rule is C
2
in
the uniform case and delivers
C
1
limit surfaces at extraordinary vertices. Kobbelt
argues that
√
3-subdivision is particularly well suited for adaptive subdivision.
Another area in which face-splitting subdivision appears to have promise is
in creating simpler interpolatory surface schemes. The advantage of face-splitting
