Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach

Подождите немного. Документ загружается.

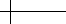
144 CHAPTER 5 Local Approximation of Global Differential Schemes

examples of slow flow include the movement of small particles through water or

air and the swimming of microorganisms [97]. Slow flow may also be viewed as a

minimum-energy elastic deformation applied to an incompressible material. This

observation is based on the fact that the flow of an extremely viscous fluid is es-

sentially equivalent to an elastic deformation of a solid. One by-product of this

view is that any technique for creating slow flows can also be applied to create

minimum-energy deformations.

Slow flows in two dimensions are also governed by two partial differential

equations. The first partial differential equation corresponds to incompressibility.

However, due to their viscosity, slow flows have a rotational component. This

rotational component is governed by the partial differential equation

(2,1)

[x, y] + u

(0,3)

[x, y] − v

(3,0)

[x, y] − v

(1,2)

[x, y] == 0.

(For a complete derivation of this equation, see Liggett [97], page 161.) If L[x, y] =

D [x]

+D[y]

denotes the continuous Laplacian, these two partial differential equa-

tions can now be written together in matrix form as



D [x] D [ y]

L[x, y]D[y] −L[x, y]D[x]



u[x, y]

v[x, y]

== 0. (5.13)

In this form, the similarity between the governing equations for perfect flow and

those for slow flow is striking: the second equation in 5.13 corresponds to the equa-

tion for irrotational flow multiplied by the Laplacian

L[x, y]. The effect of this extra

factor of

L[x, y] on the rotational component of slow flows is easy to explain: perfect

flows exhibit infinite velocities at sources of rotational flow. The extra factor of

L[x, y] smooths the velocity field at rotational sources and causes slow flows to be

continuous everywhere. For the sake of simplicity, we focus most of our analysis

on the case of subdivision for perfect flow. However, the same techniques can be

used to derive a subdivision scheme for slow flow. Those readers interested in more

details for the case of slow flow should consult [163]. The Mathematica implemen-

tation associated with this book includes code for computing approximate matrix

masks for both schemes. This code was used to compute examples for both perfect

and slow flows.

Traditionally, fluid flow has been modeled through either explicit or numerical

solutions of the associated PDEs. Explicit solutions for perfect flow are known for a

number of primitives, such as sources, sinks, and rotors. These can be combined into

more complex fields using simple linear combinations (see [97] for more details).

5.3 Subdivision for Linear Flows 145

Numerical solutions for the modeling and simulation of flow are a very active

research area. Commonly, such solutions involve approximation using either finite

difference or finite element schemes. Brezzi and Fortin [14] provide an introduction

to some of the standard numerical techniques used for modeling flow. Recently,

cellular automata have been applied with some success for the discrete modeling

of physical problems, including gas and fluid flow [21, 133].

On the computer graphics side, Kass and Miller [78] simulate surface waves in

water by approximately solving a two-dimensional shallow water problem. Chen

and Lobo [19] solve the Navier-Stokes equations in two dimensions and use the

resulting pressure field to define a fluid surface. Chiba et al. [20] simulate water

currents using a particle-based behavioral model. Miller and Pearce [106] model

viscous fluids through a connected particle system. Wejchert and Haumann [165]

introduce notions from aerodynamics to the graphics community. Stam and Fiume

[147] model turbulent wind fields for animation based on solving the underlying

PDEs. Foster and Metaxas [64] suggest solving the Navier-Stokes equations on a

coarse grid in three dimensions using a finite-difference approach and then inter-

polating the coarse solution locally as needed. They also extend their method to

handle turbulent steam [65].

5.3.2 Primal Versus Dual Subdivision

Our goal is to use the differential method of Chapter 4 in deriving vector subdivi-

sion schemes for linear flows. In the previous scalar cases, the differential method

produces a subdivision scheme that given an coarse polygon

defines a sequence

of polygons

that converge to a continuous curve p[x] approximating the initial

polygon

. In the current vector case, the differential method produces a subdivi-

sion scheme that given a coarse vector field

, v

}

on the coarse grid Z

defines a

sequence of increasingly dense vector fields

, v

}

on the finer grid

that con-

verge to a continuous vector field

{u[x, y], v[x, y]}

approximating the initial vector

field

, v

}

Before discussing the details of the subdivision scheme for flow, we first make

an important observation concerning the differential method of Chapter 4. In the

univariate case, the difference mask

[x] for the order m divided differences involves

only non-negative powers of

x and leads to a subdivision mask s[x ] for B-splines of

order

m that also only involves non-negative powers of x. As a result, the corre-

sponding B-spline basis function

n[x] is supported on the interval [0, m]. For scalar

subdivision schemes, we did not need to be careful about introducing extra powers

146 CHAPTER 5 Local Approximation of Global Differential Schemes

of x into the difference mask d

[x] and its associated subdivision mask s[x] because

these extra powers simply translated the resulting scaling function

n[x].

For vector subdivision schemes, we must be much more careful about introduc-

ing extraneous translations into the components of the vector field. For example,

translating only the first component of the flow

{u[x, y], v[x, y]}

by one unit in the

x direction yields a new flow

{u[x − 1, y], v[x, y]}

. This new flow is not a translate

of the original flow but a completely different flow. To translate the flow by one

unit in the

x direction, we must translate each component of the flow by one unit,

that is, form the new flow

{u[x − 1, y], v[x − 1, y]}

. The main consequence of this

observation is that when applying the differential method to vector schemes we

must avoid introducing extraneous shifts into the difference masks used to model

equations 5.12 and 5.13.

The solution to this problem is to center higher-order difference masks by tak-

ing powers of the centered first difference mask

d[x] = x

−

−x

. Before constructing

the finite difference equations for equation 5.11, we first consider some of the im-

plications of using half-integer powers of

x in our construction. For B-splines, using

this centered mask

d[x] in place of the uncentered mask 1 − x leads to subdivision

masks

s[x ] whose basis functions n[x] are supported on the interval [−

].Ifm is

even, the powers

cancel out, yielding a mask s[x ] involving only integral powers

x. Because m is even, the knots of the basis function n[x] remain positioned at the

integers

Z. Moreover, the coefficients attached to the integer translates of this basis

function also remain positioned on the integer grid

Z. Such schemes are known as

primal schemes. After

k rounds of subdivision for a primal scheme, the entries of

are positioned on the grid

m is odd, the situation becomes more complicated. The powers of x

do not

cancel, and the resulting mask

s[x ] involves fractional powers of x. More important,

because

m is odd, the integer translates of the basis function n[x] have knots that lie

at the midpoints of segments in the integer grid

Z. We denote the grid consisting

of such points

i +

, where i ∈ Z by D[Z]. Because B-splines are typically viewed

as having knots at the integers, this half-integer shift in

D[Z] can be cancelled by

inducing a half-integer shift in the coefficients of

[x], that is, positioning the

coefficients of

at the midpoints of segments in the integer grid

Z. In this

model,

[x] is now a generating function involving powers of x of the form x

where i ∈ D[Z]. Schemes with this structure are known as dual schemes. After k

rounds of subdivision for a dual scheme, the entries of p

are positioned on the grid

Z], that is, at the midpoints of segments in the grid

In the case of linear flow, the structure of the differential equations causes

the resulting vector subdivision schemes to have an unusual primal/dual structure

5.3 Subdivision for Linear Flows 147

Figure 5.19 Plotting the components of the discrete ﬂow {u

, v

}

on the integer grid.

that does not occur in the scalar case. In particular, the linear flows {u[x, y], v[x, y]}

defined by these schemes have the property that the u[x, y] component is primal

x and dual in y, whereas the v[x, y] component is dual in x and primal in y.In

particular, the entries of the

component of the discrete flow {u

, v

}

lie on the

grid

Z×D[

Z], whereas the entries of the component v

lie on the grid D[

Z]×

One way to visualize this discrete flow is to define a square grid passing through

the vertices of

. The entries of u

approximate flow in the x direction normal

to the vertical walls of the square grid. The entries of

approximate flow in the

y direction normal to the horizontal walls of the grid. Figure 5.19 illustrates this

positioning, with the horizontal vectors corresponding to the

component and

the vertical vectors corresponding to the

component. The length of the vectors

corresponds to the value of the corresponding entry.

As in the scalar case, the vectors

and v

can be represented as generating

functions

[x, y] and v

[x, y], with the dual component of these generating functions

involving half-integer powers of

x and y. (The associated implementation discusses

a method for implementing dual subdivision schemes with generating functions

based on integral powers of

x and y ( ).)

5.3.3 A Finite Difference Scheme for Perfect Flows

To construct the subdivision scheme for perfect flow, we first discretize differ-

ential equation 5.12 on the grid

. As suggested previously, we represent the

148 CHAPTER 5 Local Approximation of Global Differential Schemes

differential operator D[x] in terms of a centered divided difference of the form

[x] = 2

−

− x

). Under this discretization, the left-hand side of equation 5.12

reduces to



[x] d

[y]

[y] −d

[x]



[x, y]



[x] u

[x, y] + d

[y] v

[x, y]

[y] u

[x, y] − d

[x] v

[x, y]

The coefficients of the upper generating function d

[x] u

[x, y] + d

[y] v

[x, y] esti-

mate the compressibility of the discrete flow

, v

}

at the centers of squares in

. Each coefficient is associated with a square and consists of the difference of

entries in

and v

corresponding to flow entering and exiting the four sides of the

square. The coefficients of the lower generating function

[y] u

[x, y] − d

[x] v

[x, y]

estimate the rotational component of the discrete flow at grid points of

. Each

coefficient in this expression involves the difference of the four entries of

and v

corresponding to the edges incident on a particular grid point. (The discrete flow

of Figure 5.19 is incompressible but has a non-zero rotational component at each

grid point.)

Given this discretization of the left-hand side of equation 5.12, our next task is

to choose a right-hand side for equation 5.12 that relates a solution

{u[x, y], v[x, y]}

an initial coarse flow

, v

}

in an intuitive manner. One particularly nice choice is



D [x] D[y]

D [ y] −D[x]



u[x, y]

v[x, y]





i, j

rot[[ i , j]]δ[x − i, y − j]



where rot[[ i , j]]is an estimate of the rotational component of the flow {u

, v

}

at the

integer grid point

{i, j }. In terms of generating functions, rot[x, y] is the expression

[y] u

[x, y] − d

[x] v

[x, y]. Due to this particular choice for the right-hand side,

the resulting flows

{u[x, y], v[x, y]}

are divergence free everywhere and driven by

rotational sources positioned at the integer grid points

Our last task before proceeding to the derivation of the subdivision scheme is

to construct a set of finite difference equations analogous to the partial differential

equations previously given. Given that the discrete analog of the Dirac delta

δ[x, y]

is 4

, the appropriate set of finite difference equations on the grid

has the form



[x] d

[y]

[y] −d

[x]



[x, y]

== 4



rot

, y

(5.14)

== 4



−d





, y

5.3 Subdivision for Linear Flows 149

5.3.4 A Subdivision Scheme for Perfect Flows

Given the previous finite difference equation, we can now derive the associated

subdivision scheme for perfect flow. The subdivision mask for this scheme consists

of a matrix of generating functions that relates successive solutions

k−1

, v

k−1

}

and

, v

}

and has the form



[x, y]





[x, y] s

[x, y]

[x, y] s

[x, y]



k−1

, y

]

k−1

, y

]



Here, we let s

[x] denote the ijth entry of this matrix of generating functions. (Note

that we have dropped the subscript

k − 1 from s because the resulting scheme is

stationary.) The key to computing this matrix of masks is to construct an associated

finite difference equation that relates successive solutions

k−1

, v

k−1

}

and {u

, v

}

In the case of perfect flows, this two-scale relation has the form



[x] d

[y]

[y] −d

[x]



[x, y]



== 4



k−1

] −d

k−1

]



k−1

, y

]

k−1

, y

]



Substituting for {u

[x, y], v

[x, y]}

and canceling common factors of {u

k−1

, y

k−1

, y

]}

on both sides of this equation yields



[x] d

[y]

[y] −d

[x]



[x, y] s

[x, y]

[x, y] s

[x, y]



== 4



k−1

] −d

k−1

]



. (5.15)

The beauty of this relation is that the mask s

[x, y] can now be computed by

inverting the matrix of generating functions

[x ] d

[y]

[y] −d

[x ]

. The resulting matrix of

masks has the form



[x, y] s

[x, y]

[x, y] s

[x, y]



l[x, y]



d[ y] d[y

] −d[ y ] d[ x

]

−d[x] d[y

] d[x] d[x

]



, (5.16)

where d[ x] = x

−

− x

and l[x, y] = d[x]

+ d[y ]

is the discrete Laplacian mask. This

matrix

[x, y]) encodes the subdivision scheme for perfect flow. Note that this

subdivision scheme is a true vector scheme:

depends on both u

k−1

and v

k−1

. Such

schemes, although rare, have been the object of some theoretical study. Dyn [49]

investigates some of the properties of such vector schemes.

As in the polyharmonic case, the denominator

l[x, y] does not divide the

various entries in the numerators of the masks

[x, y]. In reality, this difficulty

is to be expected. Flows, even linear ones, are intrinsically nonlocal. However, just

150 CHAPTER 5 Local Approximation of Global Differential Schemes

as in the case of polyharmonic surfaces, the entries s

[x, y] of the matrix of subdivi-

sion masks can be approximated by a matrix of finite masks

[x, y] using a variant

of the linear programming technique discussed in the previous section.

To construct this linear program, we observe that due to symmetries in

x and y

in equation 5.16 the exact masks s

[x, y] satisfy the relations s

[x, y] == s

[y, x] and

[x, y] ==

[y, x]. Moreover, the coefficients of

[x, y] are symmetric in

x and y,

whereas the coefficients of

[x, y] are antisymmetric in x and y. Thus, our task

reduces to solving for approximate masks

[x, y] and

[x, y] that are symmetric

and antisymmetric, respectively.

If these masks are fixed to have finite support, we can solve for the unknown

coefficients of these approximate masks using equation 5.15. This matrix equa-

tion includes two coupled linear equations involving the exact masks

[x, y] and

[x, y]. We wish to compute approximations

[x, y] and

[x, y] to these exact

masks such that the approximate scheme is irrotational, that is,

d[ y]

[x, y] − d[x]

[x, y] == 2d[y

while minimizing the ∞-norm of the compression term

d[x]

[x, y] + d[y ]

[x, y].

Additionally, we can force the approximate vector scheme to have constant preci-

sion by enforcing the four auxiliary constraints

[1, 1] = 4,

[−1, 1] = 0,

[1, −1] = 0

[−1, −1] = 0

during the linear programming process. These four conditions in conjunction with

the fact that

[±1, ±1] == 0 (due to the antisymmetric structure of

[x, y]) au-

tomatically guarantee that the resulting vector scheme reproduces constant vec-

tor fields. The associated implementation contains a Mathematica version of this

algorithm.

Given these approximate masks, we can apply the vector subdivision scheme to

an initial, coarse vector field

, v

}

and generate increasingly dense vector fields

, v

}

via the matrix relation



[x, y]





[x, y]

[y, x]

[x, y]

[y, x]



k−1

, y

]

k−1

, y

]



5.3 Subdivision for Linear Flows 151

If the vector field {u

k−1

, v

k−1

}

is represented as a pair of arrays, the polynomial

multiplications in this expression can be implemented very efficiently using

discrete convolution. The resulting implementation allows us to model and ma-

nipulate flows in real time. Although matrix masks as small as

5 × 5 yield nicely

behaved vector fields, we recommend the use of

9 × 9 or larger matrix masks if

visually realistic approximations to perfect flows are desired.

Visualizing the discrete vector fields

, v

}

as done in Figure 5.19 is awkward

due to the fact that entries of

and v

are associated with the grids

Z ×D[

Z] and

Z]×

Z, respectively. One solution to this problem is to average pairs of entries

that are adjacent in the y direction. The result is an averaged component whose

entries lie on the grid

. Similarly, applying a similar averaging to pairs of entries

that are adjacent in the x direction yields a second component whose entries lie

on the grid

. The coefficients of these averaged components can be combined

and be plotted as vectors placed at grid points of

. Figures 5.20 and 5.21 show

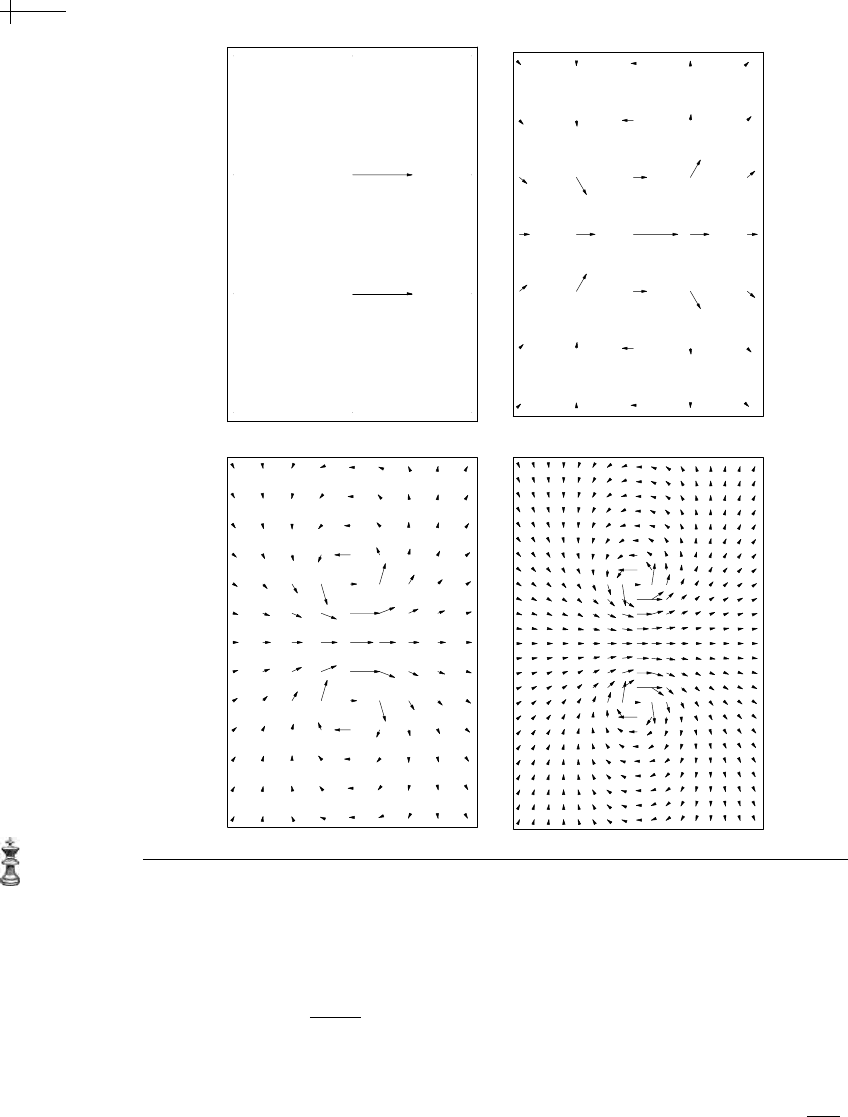
plots of several rounds of subdivision applied to a vector basis function defined in

the

x direction. Figure 5.20 uses the optimal 7 × 7 approximations

[x, y] to the

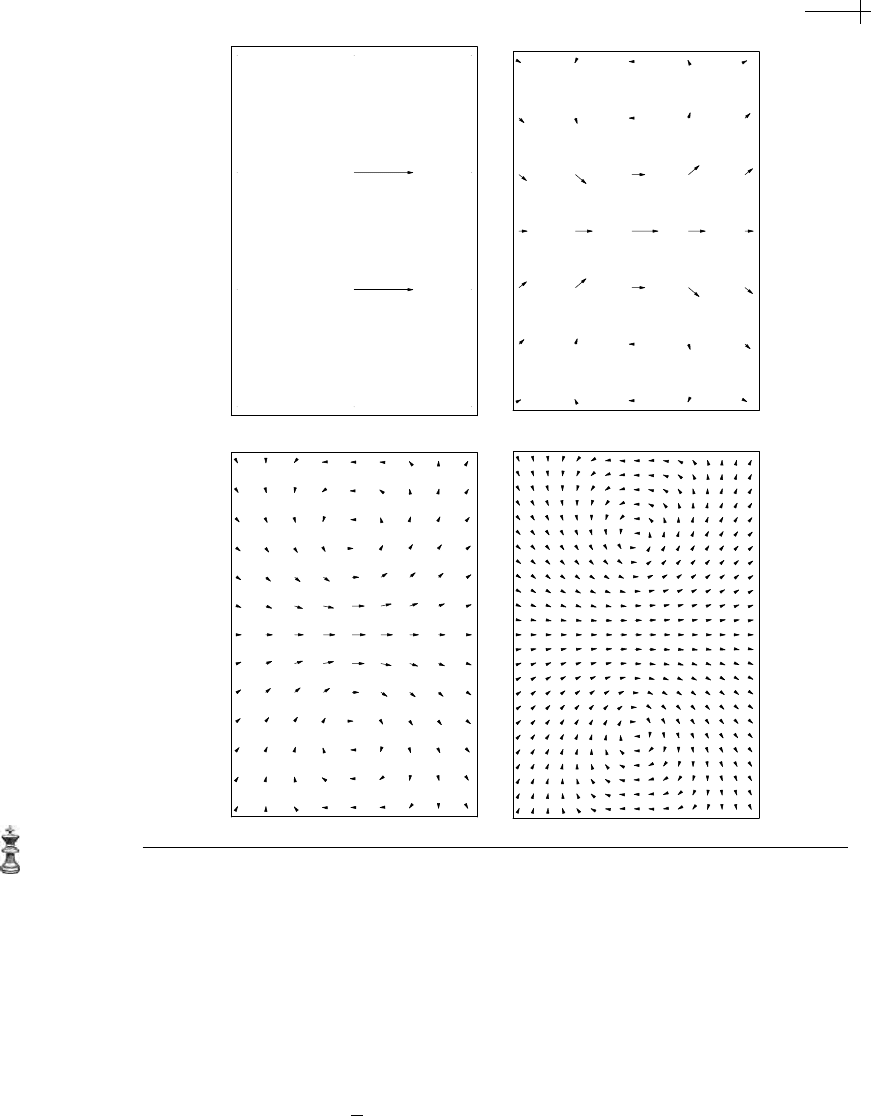
mask for perfect flow. Figure 5.21 uses the optimal

7 ×7 approximations

[x, y] to

the mask for slow flow. Figure 5.18, a slow flow, was also generated using this mask.

Note that in both cases the averaging in the

y direction has split the basis vector in

the

x direction into two separate vectors of length

. The effects of this averaging

diminish as the vector field converges to the underlying continuous flows.

5.3.5 An Analytic Basis for Linear Flows

Due to the linearity of the process, the limiting vector field defined by the sub-

division scheme can be written as a linear combination of translates of two vector

basis functions

[x, y] and n

[x, y] multiplied by the components u

and v

of the

initial vector field, respectively. Specifically, the components of the limiting field

{u[x, y], v[x, y]}

have the form



u[x, y]

v[x, y]



i ∈Z, j ∈D[Z]

[[ i , j]]n

[x − i, y − j]+



i ∈D[Z], j ∈Z

[[ i , j]]n

[x − i, y − j].

(Note that both n

[x, y] and n

[x, y] are vector-valued functions.) Our goal in this

final section is to find simple expressions for these vector basis functions in terms

of the radial basis function

c[x, y] for harmonic splines. Recall that the continuous

field

{u[x, y], v[x, y]}

is the limit of the discrete fields {u

, v

}

as k →∞. By solving

152 CHAPTER 5 Local Approximation of Global Differential Schemes

Figure 5.20 Three rounds of subdivision for a basis function in the x direction (perfect ﬂow).

equation 5.14, we can express {u

, v

}

directly in terms of {u

, v

}



[x, y]



[y]

−d

[x]



−d



, y

. (5.17)

Our task is to find continuous analogs of the various parts of this matrix expres-

sion as

k →∞. We first analyze the most difficult part of the expression,

[x , y]

5.3 Subdivision for Linear Flows 153

Figure 5.21 Three rounds of subdivision for a basis function in the x direction (slow ﬂow).

Consider a sequence of generating functions c

[x, y] such that l

[x, y] c

[x, y] = 4

for

all

k. The coefficients of the c

[x, y] are discrete approximations to the radial basis

function

c[x, y] satisfying the differential equation L[x, y] c[x, y] = δ[x, y].

The other components of this equation are easier to interpret. The differences

[x] and d

[y] taken on

converge to the continuous derivatives D[x] and D[y],