Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach

Подождите немного. Документ загружается.

134 CHAPTER 5 Local Approximation of Global Differential Schemes

focus on the Jacobi iteration due to its simplicity. For a comprehensive description

and analysis of all of these methods, the authors suggest Varga [152] and Young

[166]. Other excellent references on iterative solution methods for linear systems

include Golub and Van Loan [67], Horn and Johnson [75], and Kelly [79].

Given an initial mask

[x, y], the Jacobi iteration constructs a sequence of

masks

[x, y]. For harmonic splines (i.e., masks satisfying equation 5.8), the Jacobi

iteration has the form

[x, y] = (α ∗ l[x, y] + 1) s

i −1

[x, y] − α ∗l[x

, y

]. (5.9)

The mask (α ∗l[x, y] +1) is the smoothing mask associated with the iteration, whereas

the mask

α ∗l[x

, y

] is the correction mask associated with the iteration. For

0 ≤α ≤

, the smoothing mask takes convex combinations of coefficients of the

mask

[x, y]. For example, if α =

, the smoothing mask and correction mask have,

respectively, the form

⎛

⎜

⎝

⎞

⎟

⎠

⎛

⎜

⎝

00 000

0 −

00 000

⎞

⎟

⎠

Observe that the iteration of equation 5.9 has the property that any solution s[x, y]

to equation 5.8 is also a fixed point of the iteration.

The beauty of this iteration is that the masks

[x, y] converge to the exact

Laurent series

s[x , y] for a small range of α around α ==

. This constant α is the

relaxation factor for the iteration and controls the rate of convergence of this it-

eration. (See Young [166] for more details on the convergence of iterative meth-

ods.) If we choose an initial mask

[x, y] to be the mask for bilinear subdivision

(1+x)

(1+y)

, Figure 5.9 shows the 9×9 mask resulting from three rounds of the Jacobi

iteration.

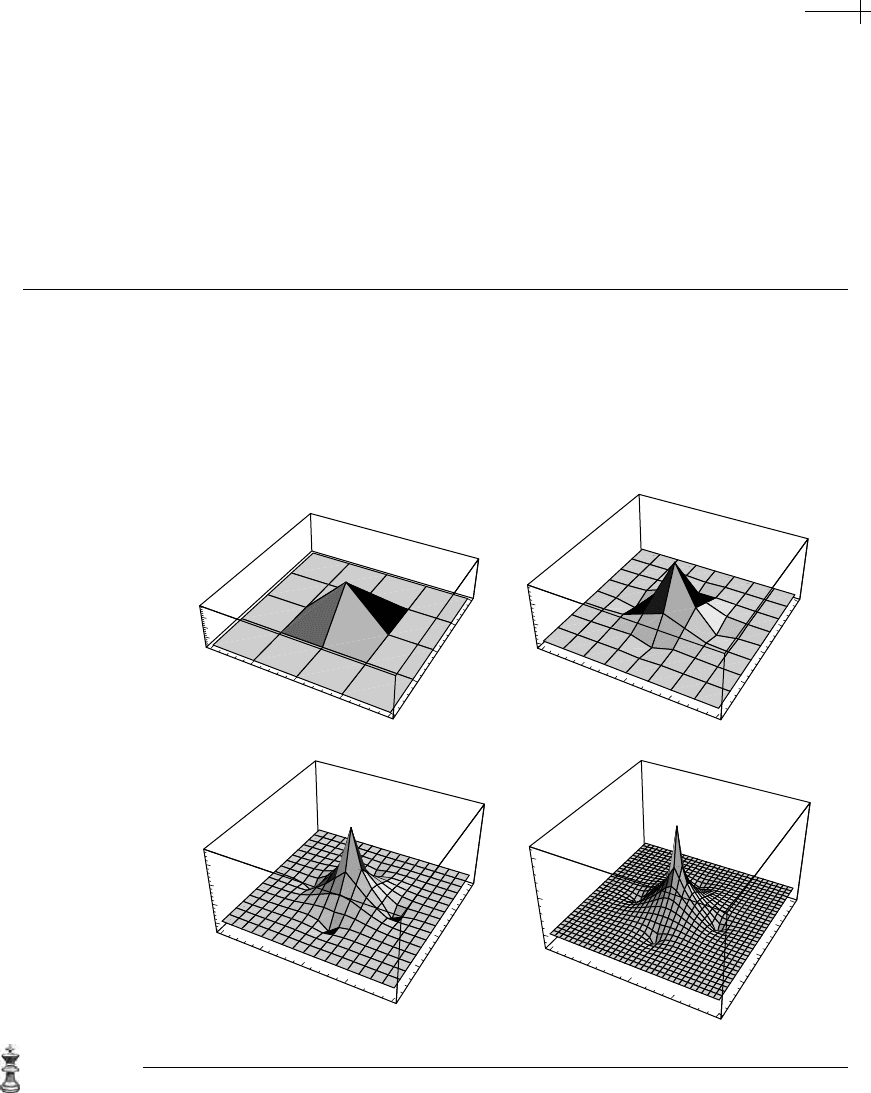
Figure 5.10 shows an approximation to the basis function

n[x, y] based on three

rounds of subdivision, with each round of subdivision using three iterations of equa-

tion 5.9. Note that although the subdivision mask of Figure 5.9 is not a particularly

good approximation of the exact mask

s[x , y] the resulting approximation of n[x, y]

is visually realistic and difficult to distinguish from Figure 5.7. Figure 5.11 shows

three rounds of subdivision applied to the initial polyhedron of Figure 5.2. Again,

this figure and Figure 5.8 are nearly indistinguishable.

5.2 Local Approximations to Polyharmonic Splines 135

0. 0. 0. 0.0012 −0.0023 0.0012 0. 0. 0.

0. 0. 0.0035 0.0069 −0.0208 0.0069 0.0035 0. 0.

0. 0.0035 0.0185 0.0382 −0.1204 0.0382 0.0185 0.0035 0.

0.0012 0.0069 0.0382 0.2361 0.4352 0.2361 0.0382 0.0069 0.0012

−0.0023 −0.0208 −0.1204 0.4352 1.4167 0.4352 −0.1204

−0.0208 −0.0023

0.0012 0

.0069 0.0382 0.2361 0.4352 0.2361 0.0382 0.0069 0.0012

0. 0.0035 0.0185 0.0382 −0.1204 0.0382 0.0185 0.0035 0.

0. 0. 0.0035 0.0069 −0.0208 0.0069 0.0035 0. 0.

0. 0. 0. 0.0012 −0.0023 0.0012 0. 0. 0.

Figure 5.9 Coefﬁcients of the mask s

[x, y] formed by three rounds of Jacobi iteration.

2

1

2

1

2

1

2

1

1.5

1

2

1

2

1

Figure 5.10 A basis function for harmonic splines constructed via subdivision based on the Jacobi iteration.

136 CHAPTER 5 Local Approximation of Global Differential Schemes

1.5

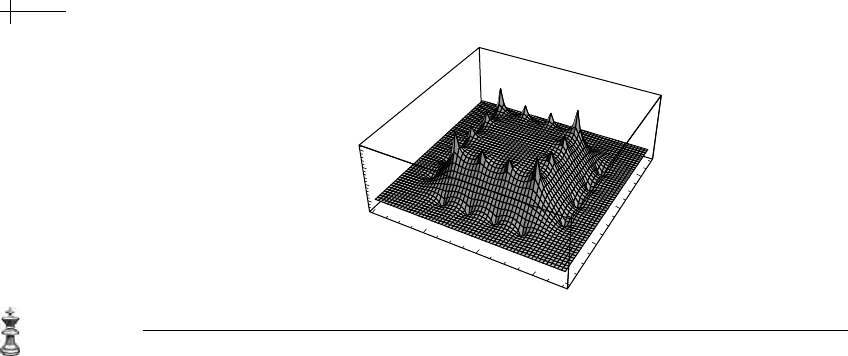
Figure 5.11 The harmonic spline of Figure 5.4 approximated by three rounds of subdivision using the

Jacobi iteration.

For differential and variational problems, the idea of expressing subdivision as

prediction using bilinear subdivision followed by smoothing with the Jacobi iteration

has been examined by Kobbelt in a number of papers [80, 82, 83, 84, 86]. Note

that the other types of iterative methods can be used in place of the Jacobi itera-

tion. For example, Kobbelt and Schr

oder [87] use cyclic reduction in constructing

subdivision schemes for variationally optimal curves. More generally, subdivision

schemes of this type can be viewed as instances of multigrid schemes [13] in which

the coarse grid correction phase has been omitted.

5.2.3 Optimal Local Approximations via Linear Programming

Our last method takes a more direct approach to constructing a local subdivision

scheme that approximates harmonic splines. Because the exact subdivision mask

s[x , y] for harmonic splines is globally supported, any locally supported scheme

has to be an approximation to the exact globally supported scheme. Our strategy

is to compute a subdivision mask

s[x, y] with a given support that approximately

satisfies

l[x, y]

s[x, y]  l[x

, y

]. If the coefficients of

s[x, y] are treated as unknowns,

this approach leads to an optimization problem in these unknown coefficients.

For harmonic splines (

m == 1), we compute a locally supported subdivision

mask

s[x, y] whose coefficients

s[[i, j]] are the unknowns. Because the bell-shaped

basis function for harmonic splines is symmetric with respect to the axes

x == 0,

y == 0 and x == y, the number of unknowns in the symbolic representation of

s[x, y]

can be reduced accordingly by reusing variable names. In particular, for fixed i, j

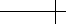
5.2 Local Approximations to Polyharmonic Splines 137

the eight unknowns

s[[±i, ±j]],

s[[±j, ±i]] are constrained to be equal. The key

to computing the remaining unknown coefficients lies in minimizing the residual

mask

r[x, y] of the form

r[x, y] = l[x, y]

s[x, y] − l[x

, y

Observe that any subdivision mask

s[x, y] that causes the residual mask r[x, y]

to be zero yields a subdivision scheme that produces solutions to equation 5.6. In

keeping with the spirit of the analysis of Chapter 3, we choose to minimize the

∞-norm of the residual mask r[x, y]; that is, minimize

Ma x





i, j

|r[[2i, 2j]]|,



i, j

|r[[2i + 1, 2j]]|, (5.10)



i, j

|r[[2i, 2j + 1]]|,



i, j

|r[[2i + 1, 2j + 1]]|



This minimization problem can be expressed as a linear programming problem in

the unknowns of the subdivision mask

s[x, y]. To construct this linear program,

we first convert the expressions

|r[[i, j]]| appearing in expression 5.10 into a set

of inequalities. To this end, we express the unknown

r[[i, j]] as the difference of

two related unknowns

[[ i , j]]− r

−

[[ i , j]], where r

[[ i , j]] ≥ 0 and r

−

[[ i , j]] ≥ 0. Given

this decomposition, the absolute value of

[[ i , j]] satisfies the inequality |r[[i, j]]|≤

[[ i , j]]+ r

−

[[ i , j]]. Observe that during the course of minimizing the sum r

[[ i , j]]+

−

[[ i , j]] one of the variables r

[[ i , j]] and r

−

[[ i , j]] is forced to be zero, with remaining

variables assuming the absolute value

|r[[i, j]]|.

Based on this transformation, minimizing expression 5.10 is equivalent to min-

imizing the variable

obj subject to the four inequality constraints



[[ 2 i , 2j]]+ r

−

[[ 2 i , 2j]] ≤ obj ,



[[ 2 i , 2j + 1]] + r

−

[[ 2 i , 2j + 1]] ≤ obj ,



[[ 2 i + 1, 2j]]+ r

−

[[ 2 i + 1, 2j]] ≤ obj ,



[[ 2 i + 1, 2j + 1]] + r

−

[[ 2 i + 1, 2j + 1]] ≤ obj .

Because the coefficients r[[i, j]] are linear expressions in the unknown coefficients

s[x, y], substituting these linear expressions for r[[i, j]] leads to a linear pro-

gram whose minimizer is the approximate mask

s[x, y]. For example, Figures 5.12

and 5.13 show the

5 ×5 and 9 × 9 masks

s[x, y], respectively, for harmonic splines.

Observe that each of these masks is an increasingly accurate approximation of the

exact mask shown in Figure 5.6.

138 CHAPTER 5 Local Approximation of Global Differential Schemes

00.0303 −0.1212 0.0303 0

0.0303 0.2424 0.4545 0.2424 0.0303

−0.1212 0.4545 1.4545 0.4545 −0.1212

0.0303 0.2424 0.4545 0.2424 0.0303

00.0303 −0.1212 0.0303 0

Figure 5.12 The optimal 5 × 5 approximation to the subdivision mask for harmonic splines.

00.0014 0.0014 −0.0014 −0.009 −0.0014 0.0014 0.0014 0

0.0014 0.0042 0.0072 0.0019 −0.0331 0.0019 0.0072 0.0042 0.0014

0.0014 0.0072 0.0211 0.0351 −0.1273 0.0351 0.0211 0.0072 0.0014

−0.0014 0.0019 0.0351 0.2445 0.4539 0.2445 0.0351 0.0019 −0.0014

−0.009 −0.0331 −0.1273 0

.4539 1.4539 0.4539 −

0.1273 −0.0331 −0.009

−0.0014 0.0019 0.0351 0.2445 0.4539 0.2445 0.0351 0.0019 −0.0014

0.0014 0.0072 0.0211 0.0351 −0.1273 0.0351 0.0211 0.0072 0.0014

0.0014 0.0042 0.0072 0.0019 −0.0331 0.0019 0.0072 0.0042 0.0014

00.0014 0.0014 −0.0014 −0.009 −0.0014 0.0014 0

.0014 0

Figure 5.13 The optimal 9 × 9 approximation to the subdivision mask for harmonic splines.

Figure 5.14 shows an approximation of the basis function n[x, y] for harmonic

splines based on three rounds of subdivision with the

9 × 9 mask of Figure 5.13.

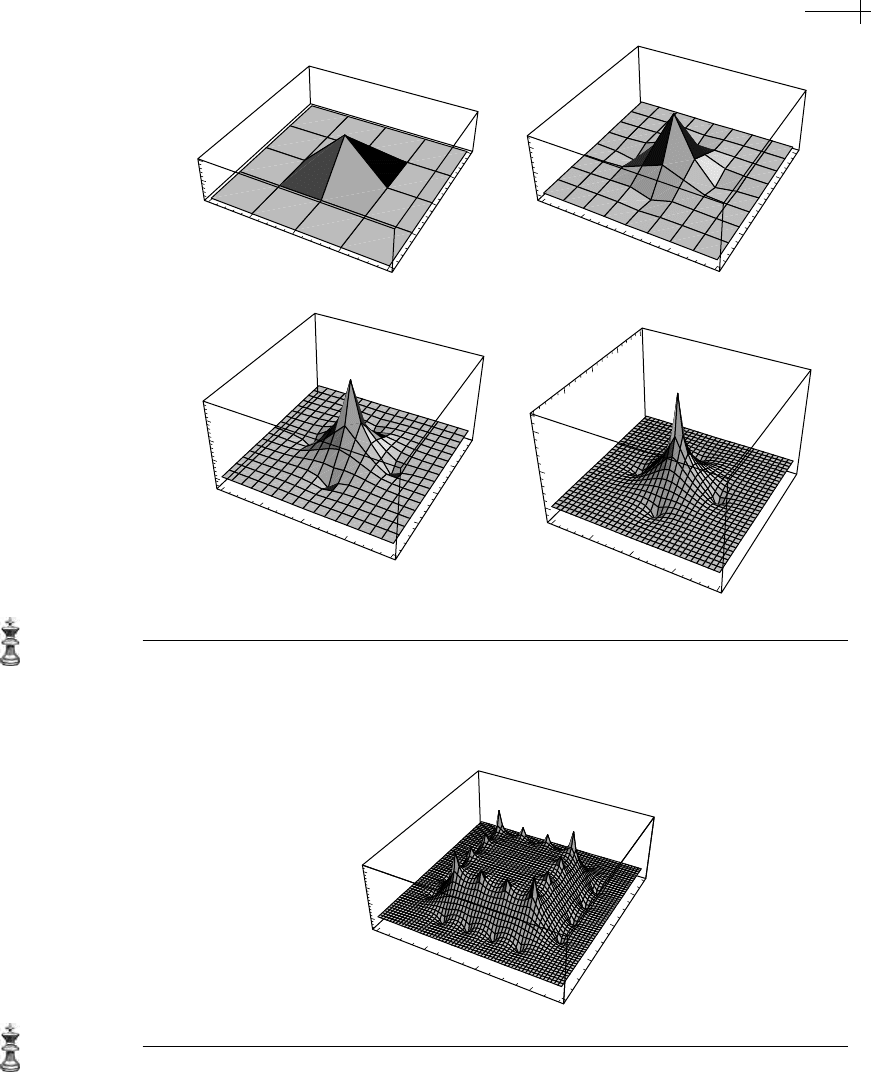
Figure 5.15 shows the result of three rounds of subdivision with this mask applied

to the initial polyhedron of Figure 5.2.

5.2.4 A Comparison of the Three Approaches

All three of the methods in this section (truncated Laurent series, Jacobi iteration,

and linear programming) provide finite approximations to the exact subdivision

mask

s[x , y] for harmonic splines. To conclude this section, we compare the accuracy

of these three methods in reproducing the exact subdivision scheme for harmonic

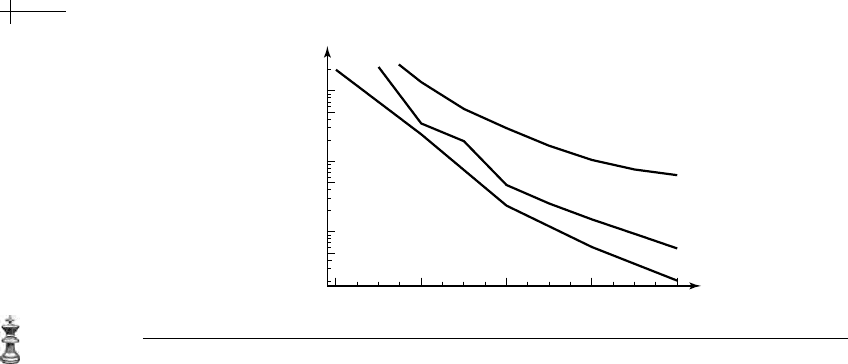
splines. Figure 5.16 shows the

∞-norm of the residual expression r[x, y] for finite

approximations of various sizes using these methods. The upper curve is the residual

plot of the Jacobi iteration, the middle curve is the residual plot for the truncated

Laurent series, and the lower curve is the residual plot for the linear programming

method. The horizontal axis is the size of the approximate mask, and the vertical

axis is the norm of the corresponding residual expression.

5.2 Local Approximations to Polyharmonic Splines 139

2

1

2

1

2

1

1.5

1

2

1

Figure 5.14 A basis function for harmonic splines constructed via subdivision based on the optimal 9 × 9

mask.

1.5

Figure 5.15 The harmonic spline of Figure 5.4 approximated by three rounds of subdivision using the

optimal 9 × 9 mask.

140 CHAPTER 5 Local Approximation of Global Differential Schemes

.005

.01

.05

(a)

(b)

(c)

Figure 5.16 Residual plots for the Jacobi iteration (a), Laurent series expansion (b), and linear programming

method (c).

As expected, the linear programming method yields masks with minimal resid-

ual. In general, the residual for the truncated Laurent mask is roughly twice that

of the optimal mask, with all of the error being distributed at the boundary of the

mask. Finite masks based on the Jacobi iteration typically have a residual that is at

least an order of magnitude larger.

One interesting question involves the behavior of these residuals during several

rounds of subdivision. The mask resulting from

k rounds of subdivision has the form

i =1

i −1

k−i

]. To measure the accuracy of this mask, we compute the norm of the

multilevel residual:

l[x, y]





i =1

i −1

k−i



−l

, y

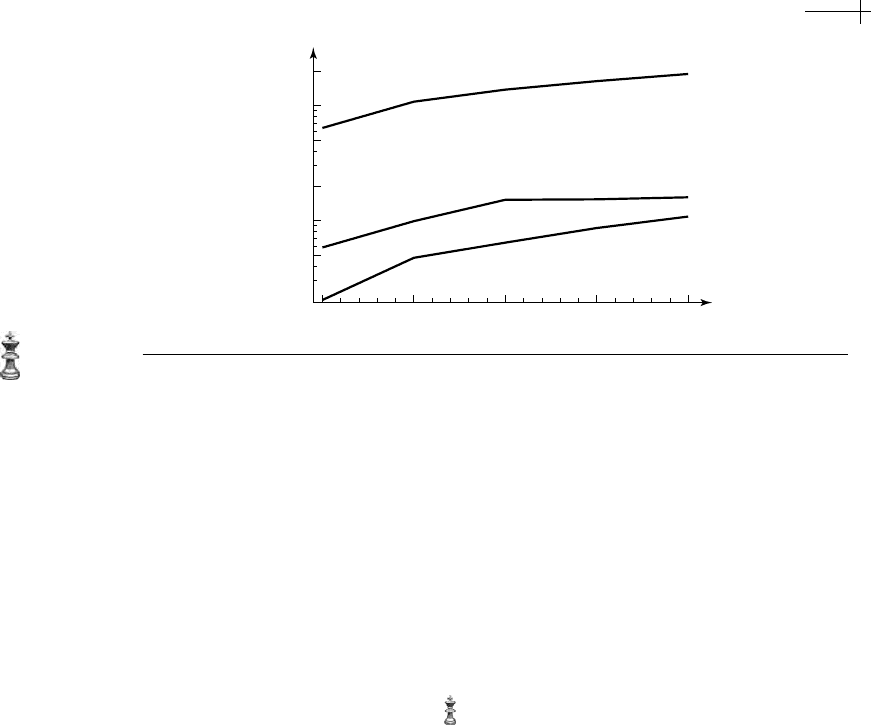
Figure 5.17 shows a plot of the multilevel residual for the masks of size 17 × 17

produced by each scheme. As before, the upper curve is the residual plot of the

Jacobi iteration, the middle curve is the residual plot for the truncated Laurent

series, and the lower curve is the residual plot for the linear programming method.

The horizontal axis denotes the number of rounds of subdivision, whereas the

vertical axis denotes the norm of the residual.

The truncation of the Laurent series expansion yields reasonable results. Be-

cause the Laurent series expansion corresponds to the exact subdivision scheme,

the only error induced is that of the truncation. Expanding the support of the trun-

cated series yields a sequence of subdivision schemes that provides increasingly

accurate approximations of polyharmonic spline surfaces. On the other hand, the

5.3 Subdivision for Linear Flows 141

12345

.002

.005

.01

.02

.05

(a)

(b)

(c)

Figure 5.17 Multilevel residuals for Jacobi iteration (a), Laurent series expansion (b), and linear program-

ming method (c).

Jacobi iteration yields masks that are substantially less accurate. In practice, a very

large number of iterations may be necessary to obtain reasonably precise solutions,

due to the slow convergence of the iteration.

The method based on linear programming exhibits the best performance in

terms of minimizing the residual. For example, the

17 × 17 mask had a residual

error of less than one percent, even after five rounds of subdivision. Although the

size of this mask might seem prohibitive, applying such larger masks during subdi-

vision can be greatly accelerated by using discrete convolution and the Fast Fourier

Transformation. The associated implementation uses this method in computing the

multilevel residual for large masks (

). For example, the multilevel residual for five

rounds of subdivision with a

17 × 17 mask was computed in less than 20 seconds

on a laptop computer. One final advantage of the linear programming approach is

that for higher-order polyharmonic splines (i.e.,

m > 1) it is easy to add extra con-

straints on the approximate mask

s[x, y] that correspond to polynomial precision

and that guarantee the conditions for convergence and smoothness of the resulting

subdivision schemes (as summarized in Chapter 3).

5.3 Subdivision for Linear Flows

Our previous examples considered the problem of constructing subdivision

schemes for scalar-valued functions (with possibly vector coefficients in the para-

metric case). In this section, we consider an extension of the techniques of the

142 CHAPTER 5 Local Approximation of Global Differential Schemes

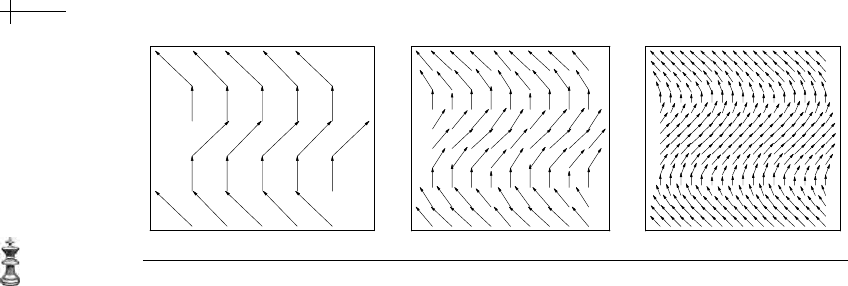
Figure 5.18 An example of subdivision for ﬂow ﬁelds.

previous two sections to the problem of constructing subdivision schemes for vec-

tor fields. Figure 5.18 shows an example of this idea. Given a coarse vector field

on the left, we wish to construct a set of subdivision rules that generate a sequence

of increasingly dense vector fields (shown on the right). If these rules are chosen

carefully, the limit of these vector fields is a continuous vector field that follows

the initial vector field. As was the case for polyharmonic splines, our approach to

constructing these rules is a differential one based on a set of partial differential

equations that model simple types of flow. This method, developed by the authors,

appears in [163].

Mathematically, flow in two dimensions is a vector-valued function

{u[x, y],

v[x, y]}

in two parameters, x and y. Flows can be visualized in a number of ways.

Perhaps the simplest method is to evaluate

{u[x, y], v[x, y]}

at a grid of parameter

values

{i , j }∈Z

. Each resulting vector {u[i , j], v[i , j]}

is then plotted, with its tail

placed at

{i, j } to form a vector field. The behavior of flows is governed by a set

of partial differential equations (PDEs) known as Navier-Stokes equations. Because

the behavior of these equations is a field of study that can occupy an entire career,

our goal is to give a brief introduction to several special cases of these equations.

The source for most of the material in this introduction is Fluid Mechanics by

Liggett [97].

5.3.1 Linear Flows

In their most general setting, the Navier-Stokes equations are nonlinear. Because

subdivision is an intrinsically linear process, it is unreasonable to expect that the

general solution to these equations can be modeled by a subdivision scheme. How-

ever, in several important settings, the Navier-Stokes equations reduce to a much

simpler set of linear PDEs. We next consider two such cases: perfect flow and slow

5.3 Subdivision for Linear Flows 143

flow. Later, we derive subdivision schemes for perfect flow, noting that exactly the

same methodology can be used to build schemes for slow flow.

Perfect flows are characterized by two properties: incompressibility and zero

viscosity. A flow

{u[x, y], v[x, y]}

is incompressible if it satisfies the partial differential

equation

(1,0)

[x, y] + v

(0,1)

[x, y] == 0.

Flows {u[x, y], v[x, y]}

satisfying this equation are said to be divergence free. In most

flows, viscosity induces rotation in the flow. However, if the fluid has zero viscos-

ity, its flows are free of rotation. Such flows are often referred to as irrotational.

Irrotational flows are characterized by the partial differential equation

(0,1)

[x, y] == v

(1,0)

[x, y].

Together, these two equations in two functions u and v uniquely characterize per-

fect flow:

(1,0)

[x, y] + v

(0,1)

[x, y] == 0,

(0,1)

[x, y] − v

(1,0)

[x, y] == 0.

(5.11)

To facilitate manipulations involving such systems of PDEs, we use two impor-

tant tools. As in the scalar case, we express various derivatives using the differen-

tial operators

D [x] and D[y]. Left multiplication by the differential operator D[x] is

simply a shorthand method for taking a continuous derivative in the

x direction; for

example,

D [x]u[x, y] = u

(1,0)

[x, y] and D[y]v[x, y] = v

(0,1)

[x, y]. Our second tool is ma-

trix notation. After replacing the derivatives in equation 5.11 with their equivalent

differential operators, the two linear equations in two unknowns can be written in

matrix form as



D [x] D[y]

D [ y] −D[x]



u[x, y]

v[x, y]

0. (5.12)

In conjunction, these techniques allow the generation of subdivision schemes from

systems of PDEs using the same strategy as employed for polyharmonic splines.

Another important class of linear flow is slow flow. A slow flow is an incom-

pressible flow in which the viscous behavior of the flow dominates any inertial

component of the flow. For example, the flow of viscous fluids such as asphalt,

sewage sludge, and molasses is governed almost entirely by its viscous nature. Other