Warren J., Weimer H. Subdivision Methods for Geometric Design. A Constructive Approach
Подождите немного. Документ загружается.

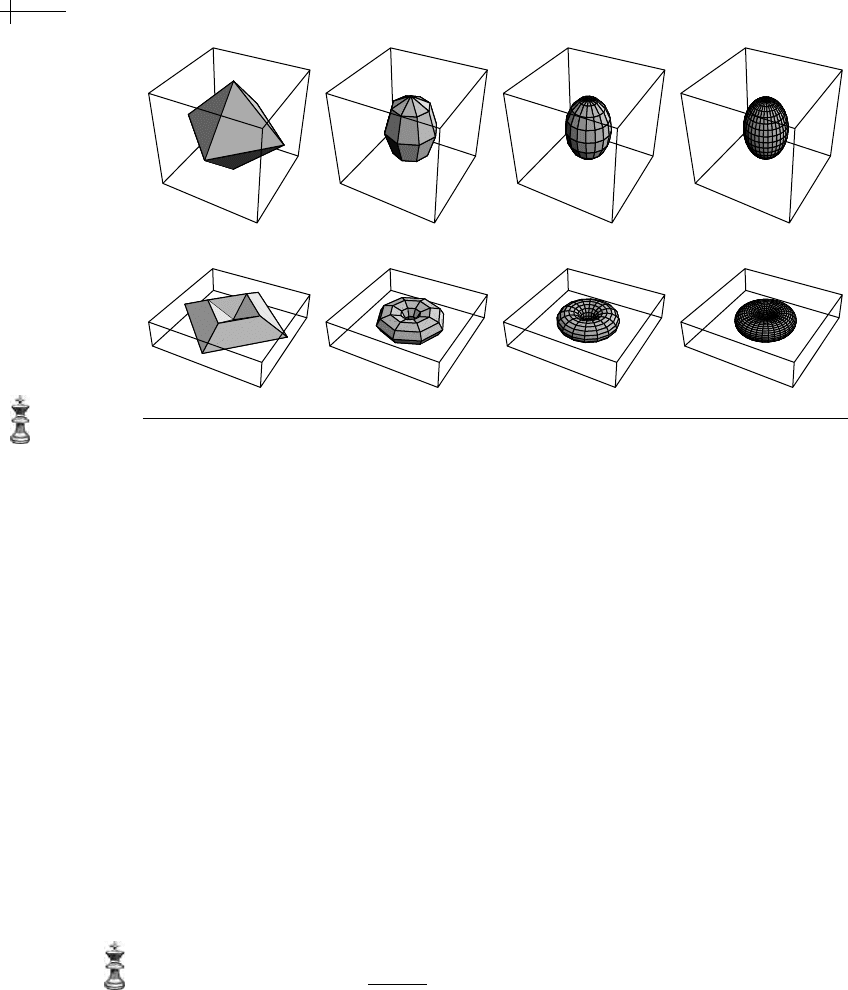
114 CHAPTER 4 A Differential Approach to Uniform Subdivision
Figure 4.5 Three rounds of subdivision for two tensor product trigonometric splines.
axis of revolution are square diamonds, the cross sections of the limit surfaces taken
along the axis of revolution are not circles, but ellipses. To generate a surface of
revolution with a circular cross section (e.g., a sphere), the reader should consult
section 7.2.3.
4.4.3 The Unified Subdivision Scheme
At this point, we have considered three examples of exponential splines of order
four: cubic B-splines, splines in tension, and mixed trigonometric splines. These
splines share enough structure that they can be viewed as instances of a single
spline scheme of order four whose segments satisfy the differential equation
p
(4)
[x] ± γ
2
p
(2)
[x] == 0. Depending on the sign and the value of ±γ
2
, this differential
equation captures the three schemes as special cases. Remarkably, the subdivision
masks for these three schemes can be expressed as a single mask
s
k−1
involving
a “tension” parameter
σ
k
. This mask depends on the tension σ
k
in the following
manner:
s
k−1
=
1
4 + 4σ
k
(1, 2 + 2σ
k
, 2 + 4 σ
k
, 2 + 2σ
k
, 1). (4.25)
For each of the three schemes, the choice of the tension σ
k
depends on the sign and
value of
±γ
2
. These cases are summarized as follows:
■
For γ == 0 (i.e., the polynomial case), let σ
k
== 1.

4.4 A Smooth Subdivision Scheme with Circular Precision 115
■
For +γ
2
(i.e., the exponential case), let σ
k
= Cosh[2
−k
γ ]. Note that in this
case
σ
k
> 1 for all k.
■
For
−γ
2
(i.e., the trigonometric case),
σ
k
= Cos[2
−k
γ ]
. The restriction 0 ≤γ ≤π
causes σ
k
to lie in the range −1 ≤ σ
k
< 1.
In all three cases, the reader may verify by inspection that equation 4.25 reproduces
the appropriate subdivision mask. At first glance, this separation of the values of
σ
k
into three cases seems to provide little help. However, the following theorem
makes these three cases unnecessary once the initial tension
σ
0
has been chosen.
THEOREM
4.4
If
σ
0
≥−1
, for all three of the previously stated cases the tensions σ
k−1
and
σ
k
satisfy the recurrence
σ
k
=
(
1 + σ
k−1
2
.
(4.26)
Proof In the polynomial case, equation 4.26 follows from the fact that 1 ==
)
1+1
2
. In the exponential case, equation 4.26 follows from the identity
Cosh[x]
2
==
1+Cosh[2x]
2
. In the trigonometric case, equation 4.26 follows from
the identity
Cos[x]
2
==
1+Cos[2x]
2
and the fact that 0 <γ ≤ π .
Given the tension σ
k−1
, the subdivision mask s
k−1
is derived by first computing
σ
k
using equation 4.26 and by then substituting σ
k
into equation 4.25. (Observe
that the mask
s
k−1
uses the tension parameter σ
k
, not σ
k−1
.) This nonstationary
subdivision scheme combines the three previous schemes in a very elegant manner.
Instead of choosing
γ , the user simply chooses an initial “tension” σ
0
. In all three
cases, the resulting limit curve is a
C
2
spline.
If the initial tension is
σ
0
= 1, then σ
k
== 1 for all k and the subdivision scheme
is exactly the cubic B-spline subdivision algorithm of Lane and Riesenfeld. If
σ
0
> 1,
the scheme converges to a spline in tension. If
−1 ≤ σ
0
< 1, the scheme converges
to a “mixed” trigonometric spline. Figure 4.3 illustrates the effect of varying initial
tensions
σ
0
on the resulting splines. In particular, the figure shows a diamond-
shaped polygon and the corresponding splines for
σ
0
={−1, 0, 1, 10, 100}. Varying
σ
0
controls the distribution of the curvature of the spline. Using large values for σ
0
causes most of the curvature to be concentrated near the vertices of the control
polygon (i.e., the spline “clings” to the control polygon). Using small values tends
to distribute more of the curvature of the spline near edges of the control polygon.
Finally, if the initial polygon
p
0
is chosen to be a regular n-gon, choosing the initial
tension
σ
0
to be Cos[
2π
n
] causes the subdivision scheme to converge to a circle.

116 CHAPTER 4 A Differential Approach to Uniform Subdivision
4.4.4 Convergence Analysis for Nonstationary Schemes
The convergence analysis of Chapter 3 considered stationary subdivision schemes,
that is, those schemes in which the mask used at each level of subdivision re-
mained unchanged. However, the subdivision schemes for exponential B-splines in
section 4.3.2 had the property that the subdivision masks
s
k−1
[x] and their corre-
sponding matrices
S
k−1
vary as a function of k. Given an initial control polygon
p
0
,
this scheme constructs a sequence of new polygons
p
k
related by p
k
= S
k−1
p
k−1
.
By construction, the limit functions
p
k
[x] associated with this scheme are C
2
.In
this section, we consider the problem of determining the smoothness of the limit
function
p
∞
[x] directly from the subdivision matrices S
k−1
.
One approach would be to follow the general method of Chapter 3 and con-
struct a subdivision scheme for various differences associated with
S
k−1
. The sub-
division matrices
T
k−1
for these schemes should satisfy D
k
S
k−1
= T
k−1
D
k−1
, where D
k
is an appropriate difference matrix. However, there are two difficulties with this
approach. First, we still have to analyze the nonstationary subdivision matrices
T
k−1
for the difference schemes. Second, for many types of nonstationary schemes, these
matrices
T
k−1
may not exist, because the subdivision scheme associated with S
k−1
is
not necessarily affinely invariant. For example, exponential B-splines are affinely
invariant (i.e., have subdivision matrices whose rows sum to one) if and only if one
of the roots
α
i
in equation 4.19 is zero.
In this section, we describe a different method, credited to Dyn and Levin
in [54], for proving that nonstationary schemes converge to
C
m
limit functions. The
key to this method is to observe that the subdivision matrices
S
k−1
for most non-
stationary schemes converge to a limit matrix
S
∞
. If this convergence is sufficiently
fast and the subdivision scheme for the matrix
S
∞
produces C
m
limit functions,
the nonstationary scheme associated with the matrices
S
k−1
also produces C
m
limit
functions. The following, weaker version of Dyn and Levin’s theorem bounds the
rate at which the matrix
S
k−1
must converge to the limit matrix S
∞
to guarantee
that the functions
p
k
[x] defined by the nonstationary scheme converge to a limit
function
p
∞
[x] that is continuous.
THEOREM
4.5
Consider a sequence of subdivision matrices S
k−1
converging to a subdi-
vision matrix
S
∞
whose rows are non-negative and sum to one. If this
convergence occurs at the rate
S
k−1
− S
∞
<βα
k−1
,
4.4 A Smooth Subdivision Scheme with Circular Precision 117
where β>0 and 0 <α<1, and the stationary scheme associated with S
∞
is
uniformly convergent, the nonstationary scheme associated with the matri-
ces
S
k−1
converges uniformly for all initial vectors p
0
with bounded norm.
Proof Because the scheme associated with S
∞
is convergent, let n[x] be its as-
sociated scaling function. Given a sequence of vectors
p
k
defined by the
nonstationary process
p
k
= S
k−1
p
k−1
, our goal is to show that the successive
functions
p
k
[x] of the form
p
k
[x] =
i
p
k
[[ i ]] n[2
k
x − i]
are converging uniformly. To prove this convergence, we examine the dif-
ference of successive functions
p
k
[x] − p
k−1
[x]. These differences can be
expressed as a linear combination of the coefficients of
(p
k
− S
∞
p
k−1
)
multiplied by translates of the scaling function n[2
k
x]. Because translates
of the scaling function
n[2
k
x] are non-negative and sum to one (due to
the rows of
S
∞
being non-negative and summing to one), the following
relation holds:
p
k
[x] − p
k−1
[x]≤p
k
− S
∞
p
k−1
(4.27)
≤(S
k−1
− S
∞
)p
k−1
≤S
k−1
− S
∞
∗p
k−1
.
Given that the norm S
k−1
− S
∞
decays geometrically in k, we next bound
the norm
p
k−1
in terms of the norm p
0
to complete the proof. To this
end, we observe that the vectors
p
k
and p
k−1
defined by the nonstationary
scheme satisfy
p
k
≤S
∞
+ (S
k−1
− S
∞
)p
k−1
≤ (S
∞
+S
k−1
− S
∞
)p
k−1
.
Because the rows of
S
∞
are non-negative and sum to one, the
∞-norm S
∞
is exactly one. Moreover, by hypothesis, S
k−1
−S
∞
<βα
k−1
and, therefore,
p
k
≤(1 + βα
k−1
)p
k−1
≤
k
i =1
(1 + βα
i −1
)
p
0
.

118 CHAPTER 4 A Differential Approach to Uniform Subdivision
The product
!
k
i=1
(1 + βα
i −1
) can be converted into an equivalent sum by
taking the logarithm of the product and then summing the logarithms of
the terms constituting the product. Because
Log[1 +] <for all >0, the
product given previously is bounded by
p
k
≤e
k
i =1
βα
i −1
p
0
≤
e
β
1−α
p
0
.
Substituting this bound into equation 4.27 and applying the hypothesis
yields
p
k
[x] − p
k−1
[x]≤βα
k−1
e
β
1−α
p
0
.
Because 0 <α<1, Theorem 3.1 guarantees that the continuous functions
p
k
[x] converge uniformly to a continuous limit function
p
∞
[x] for all
bounded
p
0
.
Requiring the rows of S
∞
to be non-negative and sum to one is actually un-
necessary and was assumed in order to simplify the proof of Theorem 4.5. Dyn
and Levin [54] give a more general proof that removes this restriction. In the case
of higher-order continuity, Dyn and Levin show that if the convergence rate of
the subdivision matrices
S
k−1
to a limit matrix S
∞
satisfies 0 <α<2
−m
and the
stationary scheme associated with
S
∞
converges to C
m
limit functions then the
nonstationary scheme associated with the matrices
S
k−1
also converges to C
m
limit
functions.
To conclude this section, we use this theorem to analyze the smoothness of the
nonstationary scheme of section 4.4.3. Given an initial tension
σ
0
≥−1, the scheme
uses subdivision masks of the form
s
k−1
[x] =
(1 + x)
2
(1 + 2σ
k
x + x
2
)
4x
2
(1 + σ
k
)
,
where σ is updated via σ
k
=
)
1+σ
k−1
2
. Given our previous analysis based on the
governing differential equation, we know that this scheme converges to a
C
2
spline-
in-tension if
σ
0
> 1,aC
2
trigonometric spline if σ
0
< 1, and a C
2
cubic B-spline if
σ
0
== 1. We now prove that the scheme is C
2
without resorting to any underlying
differential equation. Our first step is to construct a subdivision mask
t
k−1
[x] for
4.4 A Smooth Subdivision Scheme with Circular Precision 119
the second divided differences of the form
t
k−1
[x] =
(1 + 2σ
k
x + x
2
)
x(1 + σ
k
)
.
If the scheme associated with t
k−1
[x] is C
0
, the original scheme s
k−1
[x] is C
2
,asob-
served in Theorem 3.3.
To apply Theorem 4.5, our first task is to determine the behavior of
t
k−1
[x]
as k →∞. As observed previously, the tensions σ
k
converge to one as k →∞.
Therefore, the limit mask
t
∞
[x] is the subdivision mask for linear subdivision
(1+x)
2
2x
.
Because linear subdivision converges to continuous limit functions, our final task
is to bound the coefficients in
t
k−1
[x] − t
∞
[x]. After simplification, this expression
has the form
t
k−1
[x] − t
∞
[x] == −
(1 − x)
2
(1 − σ
k
)
2x(1 + σ
k
)
.
Because σ
k
≥−1, we need only establish the rate at which σ
k
converges to one. To
bound the rate of convergence, we next show that the sequence of tensions
σ
k
obeys
the bound
0 ≤
1−σ
k
1−σ
0
≤
1
2
k
for all k > 0. To establish this bound, it suffices to show
that
0 ≤
1−σ
k
1−σ
k−1
≤
1
2
. Due to the recurrence σ
k
=
)
1+σ
k−1
2
, this ratio satisfies
1 − σ
k
1 − σ
k−1
==
1
2 +
√
2
√
1 + σ
k−1
≤
1
2
,
in that
σ
k−1
≥−1
. Because linear subdivision is convergent and t
k−1
[x]
is converging
to
t
∞
[x] at the rate of O
&
1
2
k
'
, the nonstationary scheme associated with
t
k−1
[x] is also
C
0
, and therefore the original scheme associated with the mask s
k−1
[x] is C
2
.
CHAPTER 5
Local Approximation of Global
Differential Schemes
Chapter 4 described a method of constructing a subdivision mask s
k−1
[x] from the
discretization
d
k
[x] of a differential operator. In particular, these masks satisfy the
finite difference relation
d
k
[x]s
k
[x] = 2d
k−1
[x
2
]. For all three examples in Chapter 4
(polynomial B-splines, exponential B-splines, and box splines), the difference mask
d
k
[x] divides the mask d
k−1
[x
2
], yielding a finite subdivision mask s
k−1
[x]. In this
chapter, we consider two examples of differential operators for which this division
fails and for which there is no local subdivision scheme that exactly models our
physical problem.
The first section considers splines that are solutions to the polyharmonic equa-
tion
L[x, y]
m
p[x, y] == 0, where L[x, y] = D[x]
2
+D[ y]
2
is the standard Laplace operator.
These polyharmonic splines possess a globally supported, but highly localized, bell-
shaped basis that can be expressed as a difference of integer translates of the tradi-
tional radial basis function. This bell-shaped basis function possesses a refinement
relation that itself has a globally supported, but highly localized, subdivision mask.
The next section in this chapter considers three techniques for computing finite
approximations to this infinite mask: Laurent series expansion, Jacobi iteration, and
linear programming. Each method yields a locally supported subdivision scheme
that approximates the polyharmonic splines. The final section in the chapter consid-
ers the problem of generating a subdivision scheme for simple types of linear flows.
As is the case of polyharmonic splines, the subdivision mask for these flows follows
directly from the discretization of the differential operators governing these flows.
5.1 Subdivision for Polyharmonic Splines
One generalization of B-splines from the univariate setting to the multivariate set-
ting is box splines. Recalling their differential definition, box splines satisfy a partial
120
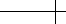
5.1 Subdivision for Polyharmonic Splines 121
differential equation whose structure depends on a set of direction vectors . One
consequence of this dependence on
is that the box-spline scaling functions are
not radially symmetric and exhibit certain directional preferences. This section con-
siders an alternative generalization of B-splines based on the differential operator
L[x, y] = D[x]
2
+ D[y]
2
associated with Laplace’s equation p
(0,2)
[x, y] + p
(2,0)
[x, y] == 0.
Due to the radial symmetry of the operator
L[x, y] (also known as the Laplace oper-
ator), the space of solutions to the partial differential equation
L[x, y]
m
p[x, y] == 0 (5.1)
is invariant under rotation. Spline surfaces that satisfy this equation (with excep-
tions possible at a set of points) are the polyharmonic splines of order
m.
Polyharmonic splines model many interesting physical phenomena. For exam-
ple, harmonic splines (
m == 1) model thin elastic membranes, heat conduction, and
electromagnetic fields. Biharmonic splines (
m == 2) model the bending behavior of
thin elastic plates. (See Powers [121] for more examples and details.) The prop-
erties of polyharmonic splines have been studied in a number of papers, including
[46, 47, 48, 72, 162].
Our approach in constructing a subdivision scheme for polyharmonic splines
follows the differential approach for polynomial splines of Chapter 4. After ini-
tially constructing the Green’s function for the polyharmonic equation, we next
construct a bell-shaped basis function by taking linear combinations of translates
of this Green’s function. This basis function is the analog of the B-spline basis
function for polynomial splines. Finally, we derive the partial differential equa-
tion that governs this bell-shaped basis function and discretize it. The subdivi-
sion mask for this new basis function follows from the resulting finite difference
equations.
5.1.1 The Radial Basis for Polyharmonic Splines
As our first step, we construct a Green’s function c[x, y] associated with the differen-
tial operator
L[x, y]
m
for the polyharmonic equation. Recall that a Green’s function
c[x, y] is a solution to the partial differential equation
L[x, y]
m
c[x, y] == δ[x, y]. (5.2)
As observed previously, this equation has many solutions. Given one Green’s func-
tion
c[x, y], any other solution to equation 5.2 has the form c[x, y] + p[x, y], where
122 CHAPTER 5 Local Approximation of Global Differential Schemes
p[x, y] is a solution to equation 5.1. Observe that any Green’s function c[x, y] satis-
fying equation 5.2 also satisfies a scaling relation of the form
c[x, y] == 4
1−m
c[2x, 2y] + p[x, y], (5.3)
where p[x, y] is a solution to equation 5.1. The key to this equation is to note that
both
c[x, y]
and 4
1−m
c[2x, 2y]
are solutions to equation 5.2, in that the Dirac delta
function
δ[x, y] satisfies a scaling relation of the form δ[x , y] = 4 δ[2x , 2y]. (The factor
of
4 arises from the fact that the integral of δ[2x, 2y] is
1
4
.)
Observe that the scaling relation of equation 5.3 is very similar to the scaling
relation for cone splines given in section 2.3.2. This similarity is no coincidence.
In fact, the Green’s functions associated with a homogeneous differential operator
always satisfy a scaling relation similar to that of equation 5.3. The existence of such
a scaling relation is often an early indication that constructing a subdivision scheme
using the integer translates of
c[x, y] is possible. Analytic solutions to equation 5.2
can be found in the literature [46, 56] and have the form
c[x, y] =
(x
2
+ y
2
)
m−1
Log[x
2
+ y
2
]
2
2m
((m − 1)!)
2
π
.
Note that we have carefully normalized the denominator in our definition of c[x, y]
such that the integral
L[x, y]
m
c[x, y] dx dy is exactly one. This integral can be evalu-
ated by restricting the range of this integral to the unit disc and then converting this
integral over the unit disc to an equivalent integral over the unit circle using Green’s
theorem. (This observation accounts for the factor of
π in the denominator.)
These functions
c[x, y] are often referred to as the radial basis functions because
the resulting functions have radial symmetry. Figure 5.1 plots some examples of
radial basis functions for small values of
m. Note the behavior of these functions
2
1
2
2
1
0
1
2
0
.05
.1
.15
1
0
2
1
0
1
2
2
1
0
1
2
.1
0
.1
2
1
2
2
1
0
1
2
0
.1
.2
.3
1
0
Figure 5.1 Radial basis function c [x, y] for polyharmonic splines of order m = 1, 2, 3.
5.1 Subdivision for Polyharmonic Splines 123
at the origin. For m == 1, c[0, 0] evaluates to
Log[0]
4π
, which is −∞.Form ≥ 2, c[0, 0]
evaluates to a constant multiple of 0 Log[0], which appears to be indeterminate.
However, taking the limit as
{x, y} approaches the origin yields c[0, 0] == 0. In fact,
closer analysis reveals that
c[x, y] has exactly 2m − 3 continuous derivatives at the
origin (i.e.,
c[x, y] is a C
2m−3
function).
For the case of
m == 2, the radial basis function c[x, y] is a smooth (C
1
) function.
One important application of this particular radial basis function is in scattered data
interpolation. Given a collection of
n points (x
i
, y
i
), each with observed values v
i
,
this interpolation problem is that of constructing a function
p[x, y] that interpolates
the data points with the observed values (i.e.,
p[x
i
, y
i
] == v
i
). Of course, many
functions satisfy this interpolation problem. To uniquely determine a solution, an
auxiliary constraint is to require this function
p[x, y] to “bend” as little as possible.
One solution to this problem is to express
p[x, y] as a linear combination of translated
radial basis functions
c[x − x
i
, y − y
i
] of the form
p[x, y] =
n
i =1
α
i
c[x − x
i
, y − y
i
].
Given the n interpolation constraints p[x
i
, y
i
] == v
i
, the coefficients α
i
are uniquely
determined. Because the radial basis function
c[x, y] satisfies the biharmonic equa-
tion (
m == 2), which models a thin sheet of clamped metal, the resulting spline
function
p[x, y] has the property that it “bends” as little as possible while interpo-
lating the desired data points. This function
p[x, y] is often referred to as a thin plate
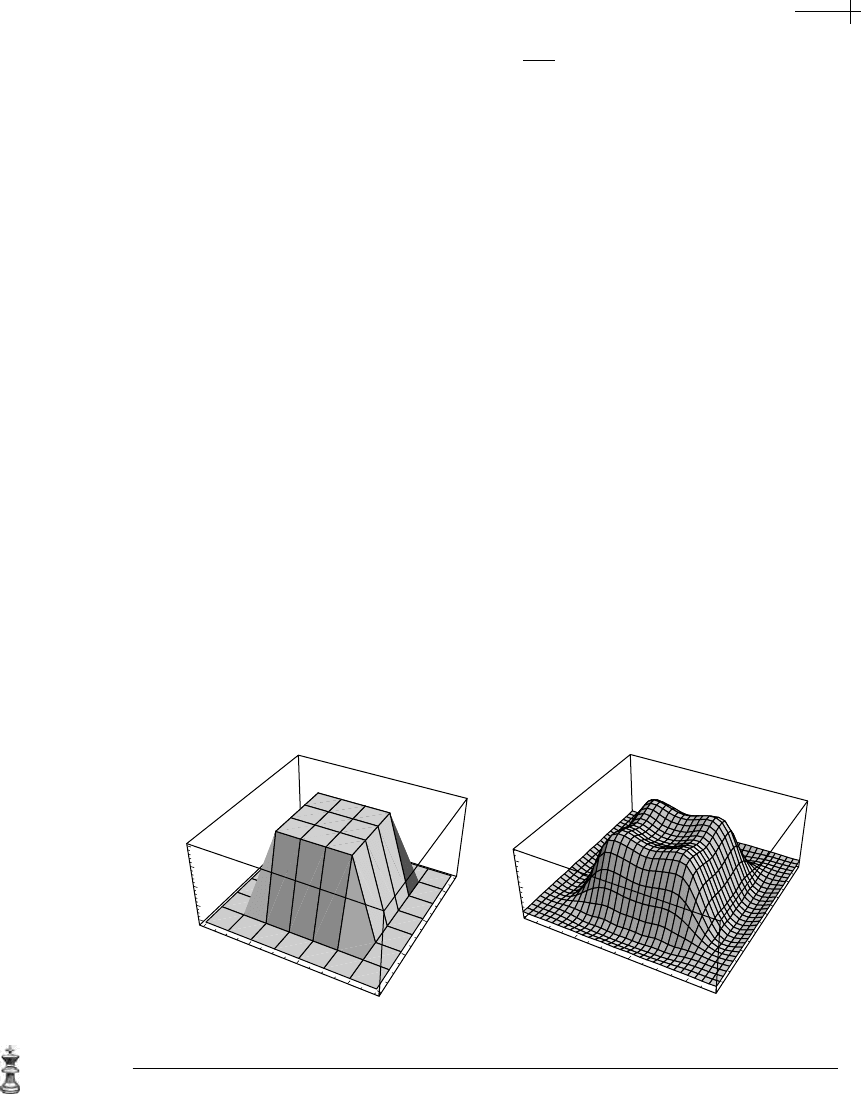
0
4
6
0
2
4
6
0
.25
.5
.75
1
2
0
2
4
6
0
2
4
6
0
.5
1
(a) (b)
Figure 5.2 Given data points (a) interpolated by a thin plate spline (b).
