Wang Zh.M. One-Dimensional Nanostructures

Подождите немного. Документ загружается.

224 B.-K. Kim et al.

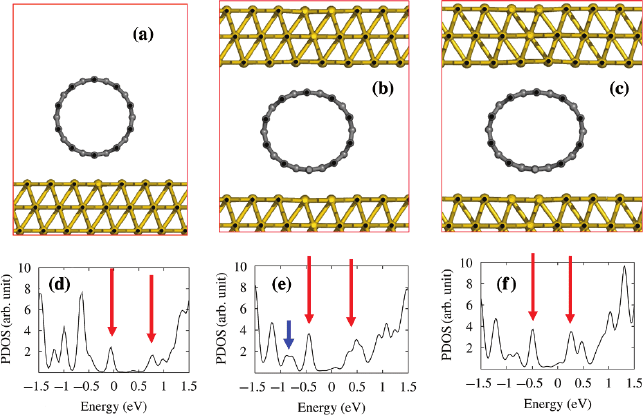
Fig. 9.5 Optimized geometries for the (10,0) carbon nanotube (a) on the Au(111) surface, and

between two gold slabs with (b) small and (c) large pressures. Panels (d), (e),and(f) show the

projected densities of states for the (10,0) carbon nanotubes for the cases of (a), (b),and(c),

respectively. Two long downward arrows in (d), (e),and(f) indicate the valence and conduction

band edges, respectively. The short downward arrow in (e) indicates the second valence band state;

the orbital characteristics of this state are depicted in Fig. 9.6

density of states (PDOS) for the nanotube are shown in Fig. 9.5. In Fig. 9.5a, only

one side of the nanotube is in contact with the gold surface. The equilibrium dis-

tance of 3.01

A indicates that the nanotube is physisorbed on the surface. Since gold

has a larger work function, the Fermi level is aligned at the valence band edge of the

carbon nanotube.

To simulate the compressing metal layers, we reduced the unit cell length of

the supercell along the z-direction, as shown in Fig. 9.5b and c. The most striking

feature of Fig. 9.5b and c is that as the nanotube–metal distance is reduced, the Fermi

level shifts up, and thus becomes aligned closer to the conduction band edge of the

nanotube, as shown in Fig. 9.5f. The calculated quantum-mechanical stresses along

the z-direction are 0.61 and 6.03 kbar for Fig. 9.5b and c, respectively. The nonzero

density of states in the band gap region is due to the metal-induced gap states. It

is also noticeable that the peaks corresponding to the second van Hove singularity

are suppressed signiﬁcantly when the nanotube is compressed by the gold slabs, as

indicated by the short downward arrow in Fig. 9.5e.

To understand these changes in the PDOS, we calculated the electronic struc-

ture of an isolated squeezed (10,0) nanotube with the same atomic geometry as in

Fig. 9.5c without the metal layers. Note that the energy gap and band dispersion

of the squeezed nanotube are almost the same as those of the pristine nanotube,

as shown in Fig. 9.6a. The isosurfaces of the three doubly-degenerate valence band

states at Γ are plotted in Fig. 9.6b, c, and d. The phase changes of the Kohn–Sham

9 Designing the Carbon Nanotube Field Effect Transistor 225

Fig. 9.6 The band structure of the isolated squeezed nanotube with the same geometry as Fig. 9.5b

without the compressing metal layers. Panels (b), (c),and(d) are contour plots of the charge density

of the three doubly degenerate states at the Γ point, as indicated by the three rightward arrows in

panel (a).The+/− signs in (b), (c),and(d) indicate the phase of the wave function. The vertical

dotted lines in (b), (c),and(d) represent the mirror reﬂection plane. Reused with permission from

Noejung Park, Donghoon Kang, and Suklyun Hong, Applied Physics Letters, 87, 013112 (2005).

wave function, indicated by +/− signs, show that the second valence state changes

most slowly along the nanotube–metal contact (dotted lines). Therefore, the hy-

bridization of this state with the Au 6s bands is easier than other valence states.

This explains why the second van Hove singularity is strongly affected, as shown in

Fig. 9.5e, by the shortening of the nanotube–metal distance. As a result, the occupa-

tion of the Au 6s bands increases, which means that the amount of charge transfer

from the CNT to the gold layer is also increased. Thus the Fermi level up-shift

shown in Fig. 9.5e and f is a consequence of the lowered local potential, which is in

turn due to the increased electron depletion in the CNT region.

The variation in the charge transfer with the pressure can be seen explicitly in the

charge density differences, ∆

[CNT/M]−

[CNT]−

[M], where M is a metal

layer. ∆

was plotted along the z-direction after averaging over the xy plane. z is the

distance from the topmost gold layer, and the arrows in Fig. 9.7c and d indicate the

edges of the CNT. Figure 9.7c shows that electronic charge accumulates on the side

of the gold surface, which indicates that the electronegativity of gold is larger than

that of the CNT. The comparison of Fig. 9.7c and d shows that electron accumulation

just above the gold surface increases when the contact is under pressure. This result

is consistent with the increased Au-C hybridization, as discussed earlier. The charge

transfer induced by the hybridization largely compensates the difference between

the local work functions of gold and the CNT, pushing the Fermi level toward the

conduction edge of the CNT. We also performed a similar calculation with other

faces of gold and found similar results.

Now we turn to the case in which strong chemical bonds have formed at the

metal–CNT interface [40,59]. In Fig. 9.8, we show that the Fermi levels of both the

gold and aluminum layers are located at the midgap of the carbon nanotube when

the metal layers and the carbon nanotube are chemically bonded. This suggests that

the Fermi level of the metal is strongly pinned at the midgap of the CNT, irrespective

226 B.-K. Kim et al.

Fig. 9.7 Optimized geometries for the (10,0) carbon nanotube (a) on the Au(111) surface and (b)

between two gold slabs. The charge density differences, as deﬁned in Fig. 9.2, for the conﬁgura-

tions (a) and (b) are plotted along the direction perpendicular to the metal surface in (c) and (d),

respectively. Two upward arrows in (a)–(d) indicate the edges of the nanotubes. Reused with per-

mission from Noejung Park, Donghoon Kang, and Suklyun Hong, Applied Physics Letters, 87,

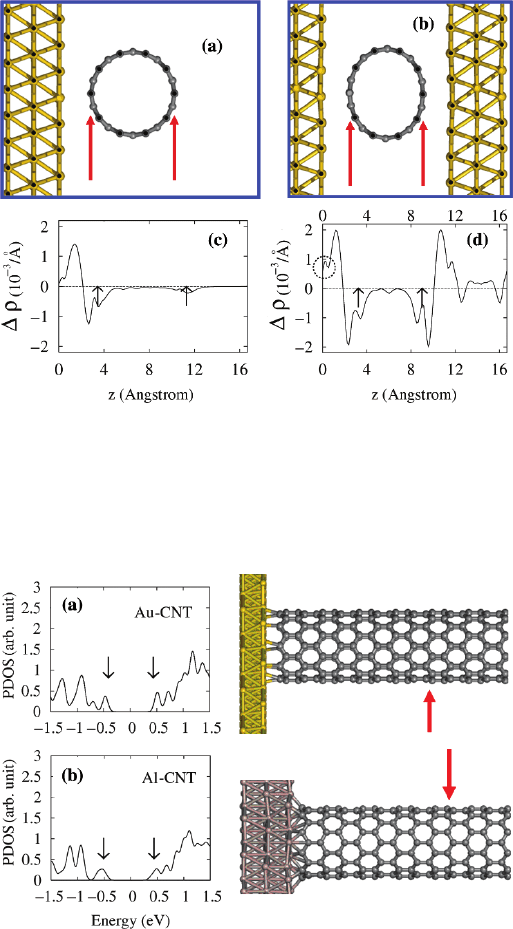
Fig. 9.8 Electronic structures and bonding conﬁgurations of (a) Au layers and (b) Al layers in

end-contact with a semiconducting (10,0) CNT. Partial densities of states (PDOS) for 20 carbon

atoms of the CNT, which is the 9th zigzag chain from the metal surface, indicated by the red

arrows in the atomic geometries, are shown with respect to the Fermi level of each conﬁguration.

The two downward arrows in the PDOS indicate the valence and conduction band edges. In these

calculations, the 10 nm long CNT is connected to the metal at both ends, but only one end part is

shown. Reused with permission from Sunkyoung Moon, Sun-Gul Lee, Woon Song, Joon Sung Lee,

Nam Kim, Jinhee Kim, and Noejung Park, Applied Physics Letters, 90, 092113 (2007). Copyright

2007, American Institute of Physics

9 Designing the Carbon Nanotube Field Effect Transistor 227

of the metal work function. On the basis of these results, we suggest that the micro-

scopic differences between the metal–CNT interfaces are very important inﬂuences

on the Schottky barrier. The adsorption states and bonding conﬁgurations at the

metal–CNT interface are also likely to substantially affect the transport behavior of

SWNT-FETs. This also means that engineering of the metal–CNT interface could

be exploitable to achieve SWNT-FETs with desired conduction patterns.

9.3 Metal–Carbon Nanotube Contact Engineering

In this section, we describe various experimental techniques for controlling the

height of the Schottky barrier at metal–nanotube contacts, and their effects on the

electronic transfer properties of SWNT-FETs. By controlling the Schottky barrier

height, it is possible to fabricate electronic devices such as diodes and n-type transis-

tors that are necessary for logic circuits, and the delicate modulation of the Schottky

barrier can be used to develop highly sensitive SWNT-FET based sensors.

9.3.1 Fabrication of Carbon Nanotube Diodes with Contact

Engineering

In this section, we focus on the fabrication of a SWNT device that operates as a

rectifying diode. Several research groups have fabricated SWNT-based diodes, ei-

ther by using conventional approaches such as selective doping of part of the nan-

otube, or by adopting local split gates to control the carrier concentration in the

nanotube [1, 15, 31, 60]. However, by exploiting the well-known characteristics of

the Schottky barriers of SWNT-FETs, it may be possible to construct a SWNT-based

diode simply by adjusting the Fermi-level lineup at the nanotube–metal contact.

We tested this suggestion by fabricating symmetric p-type SWNT-FETs with

high work function metals, and then converted these devices into Schottky diodes

by modifying one of the contact barriers with a self assembled monolayer (SAM)

of molecules containing a thiol group.

The SWNT-FETs used in this study were fabricated with the patterned growth

method [27b.] and conventional photolithography followed by lift-off. The sample

fabrication procedure was as follows. First, catalyst patterns were created on a heav-

ily doped p-type Si wafer with 500 nm thermal oxide by using a deep-UV mask-

aligner, and the samples were allowed to react with Fe/Mo catalyst in methanol

for 10 ∼ 30s. The samples were lifted off in boiling acetone, and washed three

times with fresh acetone and isopropanol. The samples with patterned catalyst were

then transferred to a furnace, where nanotube growth was carried out in a CH

and

atmosphere at 900

◦

C. The electrode patterns were fabricated with photolithog-

raphy, and 5 nm titanium and 20 nm Au were evaporated successively using ther-

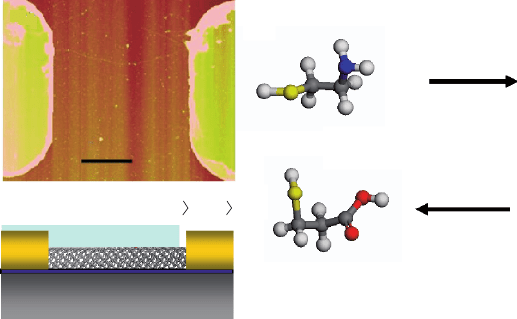
mal evaporation. Figure 9.9a shows an AFM image of the bare device used in our

228 B.-K. Kim et al.

(a) (c)

(b)

2 µm

SU-8

3-Mercaptopropionic acid

N H

2-Aminoethanethiol

−

Fig. 9.9 (a) AFM image of the device used in these experiments. (b) Schematic drawing of a

SWNT-FET with a SAM on one contact. (c) Molecular structures of the two self-assembling mole-

cules used in this study. Reused with permission from Byoung-Kye Kim, Ju-Jin Kim, Hye-Mi So,

Ki-Jeong Kong, Hyunju Chang, Jeong-O Lee, and Noejung Park, Applied Physics Letters, 89,

experiments (i.e., before SAM treatment). Patterns were created on this bare device

with an SU-8 negative photoresist to expose one of the contacts for chemical treat-

ment, as depicted in Fig. 9.9b. Two self-assembling molecules, 2-aminoethanethiol

(HSCH

NH; Mw 77.15), and 3-mercaptopropionic acid (HSCH

Mw 106.14) were purchased from Sigma-Aldrich, and used without further treat-

ment. These molecules were selected because they each contain a thiol group, which

is well known to favor the formation of highly ordered monolayers on Au sur-

faces [54a.]. Figure 9.9c shows the molecular structures of 2-aminoethanethiol and

3-mercaptopropionic acid, and the predicted directions of the dipole moments of the

pristine molecules.

The electrical transport characteristics of the devices were recorded prior to

molecular treatment, and then the devices were reacted with a 10 mM solution of

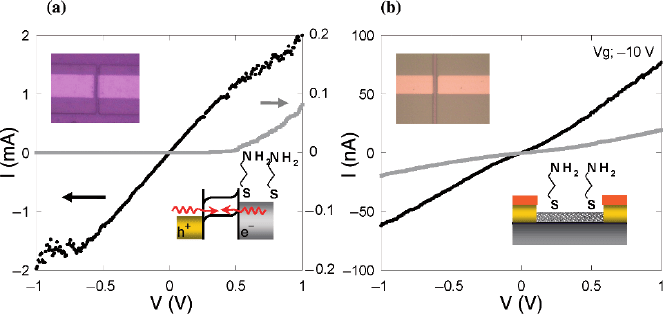
self assembling molecules in ethanol. Figure 9.10 shows the I–V characteristics of

the SWNT-FET before (black curve) and after treatment of the exposed contact

with 2-aminoethanethiol (gray curve; reaction time of 10 min). The upper left inset

shows an optical microscopy image of the device, and the lower right inset shows

the band diagram after the 2-aminoethanethiol treatment. As shown in Fig. 9.10a,

a symmetric I–V curve was observed before introduction of the SAM. After the

2-aminoethanethiol treatment, in contrast, the device exhibits highly asymmetric,

diode-like I–V characteristics.

For comparison, we fabricated a device in which both contact electrodes were

covered with SU-8, exposing only the nanotube body region. After treatment of

these SU-8-covered electrodes with 2-aminoethanethiol, the device was found to ex-

hibit symmetric I–V characteristics with decreased conductance (Fig. 9.10b). This

result is consistent with those of Kong et al., who attributed this conductance de-

crease to the electron doping nature of the amine groups [26]. When we used a

3-mercaptopropionic acid SAM in similar experiments, no signiﬁcant changes in

the transport characteristics were observed (data not shown).

9 Designing the Carbon Nanotube Field Effect Transistor 229

Fig. 9.10 (a) I–V curves measured before (black, at V

= 0) and after treatment of the surface

with 2-aminoethanethiol (gray curve). Upper inset: optical microscopy image of the single-contact

open device. Lower inset: schematic band diagram of the device. (b) I–V curves before (black) and

after (gray) 2-aminoethanethiol treatment of the contact-passivated device. Reused with permission

from Byoung-Kye Kim, Ju-Jin Kim, Hye-Mi So, Ki-Jeong Kong, Hyunju Chang, Jeong-O Lee, and

Physics

The diode-like operation of the SWNT-FET with a 2-aminoethanethiol SAM can

be explained by the formation of asymmetric contacts after the molecular treatment

of the cathode surface, as depicted in the inset in Fig. 9.10a. To fabricate the Schot-

tky diode, we used a self assembly technique to adjust the Fermi-level lineup of the

predeﬁned nanotube transistor. A similar self assembly approach has been used to

control the Schottky barrier height in organic electronic devices. [7, 10] For com-

parison, we used two molecules, 2-aminoethanethiol and 3-mercaptopropionic acid,

which were expected to have different dipole directions (see Fig. 9.9c). We found

that only treatment with 2-aminoethanethiol resulted in diode-like operation.

We investigated the different effects of adding the 2-aminoethanethiol and

3-mercaptopropionic acid molecules to a bare Au surface by carrying out ab initio

electronic structure calculations. We used the calculation method described in our

previous study [41a.]. Here we adopted a slab geometry with six gold layers, in

which the two layers in the center were ﬁxed during the geometry optimization

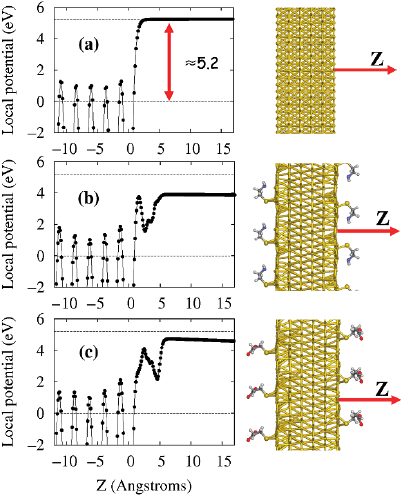
calculation. Plotting the local potential with respect to the Fermi level, we obtained

the work function of the bare Au surface and of the Au surfaces with adsorbed

2-aminoethanethiol and 3-mercaptopropionic acid, as shown in Figs. 9.11a, as well

as 11b, and c, respectively. The calculated work function of the bare Au surface

(≈5.2eV) is very close to the previously reported value [36]. The work functions

of the Au surfaces with adsorbed 2-aminoethanethiol and 3-mercaptopropionic

acid (Fig. 9.11b and c) are signiﬁcantly different. Speciﬁcally, the adsorption of

2-aminoethanethiol molecules substantially decreases the work function (≈3.9eV),

whereas the adsorption of 3-mercaptopropionic acid has little effect (≈4.7eV).This

difference conﬁrms that the asymmetric I–V pattern observed after treatment of one

230 B.-K. Kim et al.

Fig. 9.11 Plots of the local potentials with respect to the Fermi level of (a) thebare6layersofAu,

(b) the 6 layers of Au with adsorbed 2-aminoethanethiol molecules, and (c) the 6 Au layers with

adsorbed 3-mercaptopropionic acid molecules. Reused with permission from Byoung-Kye Kim,

Ju-Jin Kim, Hye-Mi So, Ki-Jeong Kong, Hyunju Chang, Jeong-O Lee, and Noejung Park, Applied

electrode of the SWNT-FET with 2-aminoethanethiol was due to a change in the

Schottky barrier at the treated contact.

To investigate the effect on the transfer characteristics of treatment with

2-aminoethanethiol, we measured the evolution of the I–V

characteristics of the

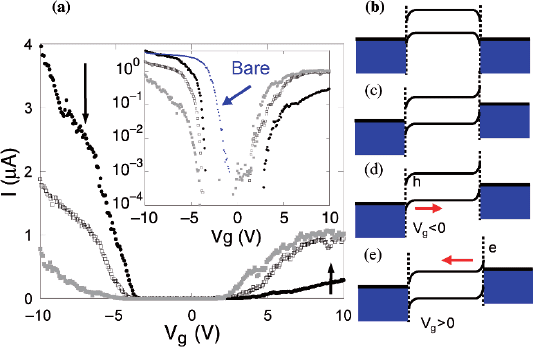
SWNT-FETs, as shown in Fig. 9.12a. Before the reaction with 2-aminoethanethiol,

the device exhibits typical p-type transistor behavior (black circles). After treat-

ment with 2-aminoethanethiol for 10 min (empty squares) and 5 h (gray symbols),

however, the p-channel conduction decreases and n-type conduction becomes

dominant, as indicated by the solid arrows in Fig. 9.12a. The effect of adding the

2-aminoethanethiol SAM seems to saturate after a reaction time of about 5 h, with

the I–V

characteristics remaining almost unchanged upon further treatment. As

a result, the SWNT-FET with a 2-aminoethanethiol SAM on one contact exhibits

ambipolar transfer characteristics.

The ambipolar transfer characteristics can be explained by considering the band

diagram for a device with asymmetric contacts, as generated by SAM treatment of

one contact. Before the SAM treatment (Fig. 9.12b), the Fermi levels of the elec-

trodes are aligned with the valence band of the carbon nanotube, leading to p-type

behavior. After the formation of the 2-aminoethanethiol SAM (Fig. 9.12c), how-

ever, the Fermi level of the cathode is aligned with the conduction band edge. For

9 Designing the Carbon Nanotube Field Effect Transistor 231

Fig. 9.12 (a) The evolution of the electrical transfer characteristics with the formation of a

2-aminoethanethiol SAM: before reaction (black circles); after 10 minutes of reaction (empty

squares); and after 5 h of reaction (gray squares). The inset shows a log-scale plot. The band

diagram of the SWNT-FET (b) before and (c) after SAM treatment. The band diagram of the

SWNT-FET with one contact modiﬁed for (d)V

< 0and(e) V

> 0. Reused with permission from

Byoung-Kye Kim, Ju-Jin Kim, Hye-Mi So, Ki-Jeong Kong, Hyunju Chang, Jeong-O Lee, and

of Physics

a SWNT-FET with a SAM-modiﬁed electrode, the hole current would still dominate

when V

< 0, as shown in Fig. 9.12d. However, signiﬁcant electron conduction will

occur in the SAM-modiﬁed device when V

> 0, as shown in Fig. 9.12e. As a result,

the device exhibits ambipolar transfer characteristics.

It is also noteworthy that the threshold voltage of the device does not change

signiﬁcantly after the SAM treatment of one of the contact electrodes, as shown

in Fig. 9.12a. It is well known that shifts in the threshold voltage are largely due

to variations in the doping level in the semiconductor channel region, whereas

changes in the slope of I–V

curves are due to variations in the Schottky barrier

at the contact [12]. As shown in Fig. 9.12a, the 2-aminoethanethiol treatment in-

duces slope changes in the I–V

curve, eventually resulting in ambipolar behavior,

with no prominent shifts in the threshold voltage. These ﬁndings conﬁrm that the

introduction of the 2-aminoethanethiol SAM modiﬁes the Schottky barrier at the

engineered contact.

In summary, we have fabricated a p-type SWNT-FETs and then converted it into a

diode bytuning the Schottkybarrier height using a SAM technique. Highly asymmet-

ric, diode-like I–V curves were observed when one of the contacts was functionalized

with a 2-aminoethanethiol SAM. Ab initio electronic structure calculations con-

ﬁrmed that the adsorption of 2-aminoethanethiol onto an Au surface induces a strong

decrease in the work function, whereas the adsorption of 3-mercaptopropionic acid

has little effect. These results indicate that tuning the Schottky barrier by introducing

a SAM of a selected molecular species could be a practical method to control the

conduction patterns of nanotube-based electronic devices.

232 B.-K. Kim et al.

9.3.2 Fabrication of n-Type Single-Walled Carbon Nanotube

Transistors with Al Decoration

In this section, we discuss the fabrication of n-type SWNT-FETs using a controlled

in situ Al decoration technique. By using the Al decoration technique, Schottky

barrier control and channel doping are possible at the same time, and it is possible

to compare the effects of channel doping with those of contact-barrier control.

The same sample fabrication process as described in the previous section was

used. Bare SWNT-FETs (open devices) were prepared, and contact-decorated

SWNT-FETs or channel-decorated SWNT-FETs were prepared by using an SU8-

2002 negative photoresist or a PMMA mask.

For the in situ electrical measurements, the samples were wired to a chip con-

nected to electrical feedthrough in an evaporation chamber. For Al decoration, the

vacuum chamber was pumped down to 2 ×10

−6

torr, and the Al source was slowly

evaporated by using an electron beam while monitoring the conductance of the

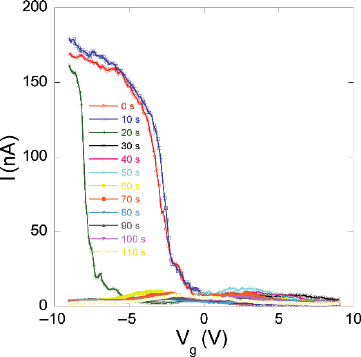
SWNT-FETs. Figure 9.13 shows the variation of the electronic transfer character-

istics of the SWNT-FETs with controlled Al deposition. Upon Al deposition, the

electronic transfer curves shift toward more negative gate voltages. The curves

were obtained by carrying out measurements every 10 s: it can be seen that p-

type conduction disappears completely after about 30 s. The deposition rate was

carefully kept below 0.1

A/s. After about 2–4 min deposition, the p-type SWNT-

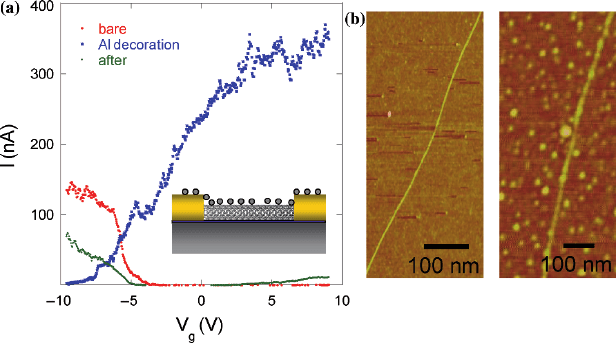
FETs were converted into n-type SWNT-FETs. Figure 9.14 shows the changes in

the electronic transfer characteristics and AFM images of an open SWNT-FET. For

this sample, about 30

A thick Al was deposited while monitoring the conductance.

As shown in Fig. 9.14a, the sample exhibits enhanced n-type conduction follow-

ing the Al deposition. The doping level of the Al-decorated n-type SWNT-FET

Fig. 9.13 The changes in the electronic transfer properties of an open SWNT-FET resulting from

in situ Al decoration

9 Designing the Carbon Nanotube Field Effect Transistor 233

Fig. 9.14 (a) The changes in the electronic transfer properties of the device resulting from Al dec-

oration. (b) AFM images of the device. Reused with permission from Hyo-Suk Kim, Byoung-Kye

Kim, Ju-Jin Kim, Jeong-O Lee, and Noejung Park, Applied Physics Letters, 91, 153113 (2007).

can be controlled by varying the Al deposition time. In this particular device, the

on/off ratio of the n transistor is about 10

, and channel pinch off does not occur

until V

= −10V. Upon adsorption of Al onto the carbon nanotube, electrons will

be transferred from Al to the carbon nanotube, since Al has a lower work func-

tion (4.1 eV) than the nanotube (4.8 eV). Further, the presence of Al clusters in the

contact region can lower the height of the Schottky barrier to electron transport.

However, the device gradually became a p-type SWNT-FET again when exposed to

air. Such phenomena are attributed to the oxidation of Al and the subsequent work

function increase, as indicated by electronic structure calculations in Sect. 9.2.1.

Similar behavior was observed for the contact-decorated and channel-decorated

devices; the devices become n-type transistors after decoration, and are gradually

converted back to p-transistors in air. Channel-decorated devices exhibit decreased

conductance after Al decoration, whereas improved transistor performance was

observed in the contact-decorated devices. The controlled deposition of metallic

nanoparticles can thus be an effective method for the fabrication of complementary

SWNT-FETs and highly sensitive sensor devices, though care must be taken not to

introduce oxygen into the system.

9.3.3 The Effects of Metal Clusters on Carbon Nanotube Sensors

In the previous section, we showed that it is possible to fabricate n-type nanotube

transistors by decorating low work function metals onto nanotubes. In this section,

we discuss the effects of the decorated metal particles on the sensing characteris-

tics of SWNT-FET based chemical sensors and how the change in work function

affects them.