Wallace J.M., Hobbs P.V. Atmospheric Science. An Introductory Survey

Подождите немного. Документ загружается.

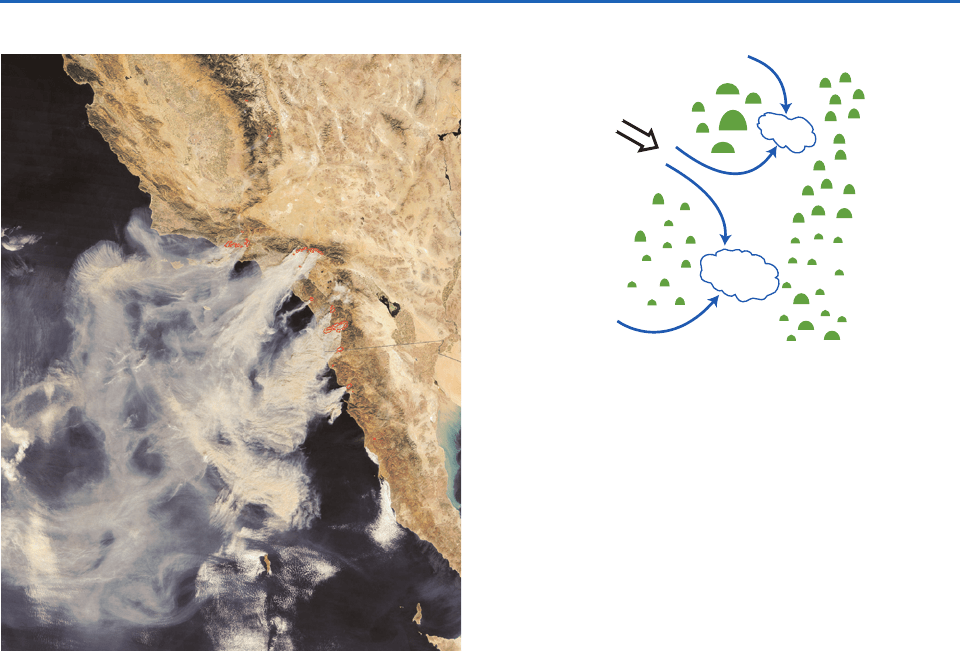
344 Weather Systems

sometimes develop in response to lee cyclogenesis, as

air flowing around the two sides of the mountain

range converges and lifts the air above it, triggering

convection, as illustrated schematically in Fig. 8.41.

A necessary condition for the formation of such a

downwind convergence zone is the presence of condi-

tional instability, which enables the converging air to

ascend without being unduly inhibited by the static

stability.

Mountain ranges can also give rise to dramatic

spatial variations in freezing level. Under conditions

of cold air damming, with colder air and higher pres-

sure to the east side of a range, the approach of a

cyclone or trough of low pressure from the west

increases the pressure gradient across the range,

drawing cold air up and over the mountain passes.

Freezing levels in this cold, upslope flow tend to be

much lower than in the free atmosphere. Hence,

under these conditions, frozen precipitation may be

falling in the passes while rain is falling at higher ele-

vations. Freezing rain occurs much more frequently

in the lowlands along the east side of mountain

ranges, in association with cold air damming, than on

the west side. The drainage of cold air through a gap

in a mountain range can sustain frozen precipitation

on the west side (often in the form of sleet and freez-

ing rain) even when the ambient surface air tempera-

ture is well above freezing.

8.3 Deep Convection

Among the most striking features in time-lapse satel-

lite imagery are clouds formed by the spreading

of updrafts in deep cumulus convection as they

approach the tropopause. Deep convection tends to

be concentrated within certain preferred regions

such as the summer monsoons, persistent bands of

low level convergence like the ITCZ, over and along

the slopes and crests of mountain ranges, and within

the frontal zones and warm sectors of extratropical

cyclones. Global surveys indicate that at any given

time, cirriform anvil clouds formed in this manner

cover only a few percent of the surface area of the

Earth, and active convection occupies only a small

fraction of the surface area beneath those clouds.

Yet despite its small areal coverage, deep convection

and its associated stratiform precipitation account

for most of the rainfall in the tropics and over the

continents of the summer hemisphere.

Fig. 8.40 Dispersion of the smoke plumes from a massive

outbreak of California wildfires on October 26, 2003, during

a nearly week-long episode of hot, dry, northeasterly Santa

Ana winds. Red pixels denote the locations of the fires at this

time. Of the three large clusters of fires in the image, the

middle one is located east of Los Angeles and the southern

one near San Diego. The fires raged out of control until the

winds subsided and shifted 2 days later. [NASA Terra MODIS

satellite imagery.]

Fig. 8.41 Schematic of low level airflow through gaps on an

extended mountain range converging into terrain-induced

cyclones on the lee side of the range, giving rise to the devel-

opment of rain bands. If air simply flowed over the mountains

rather than around them, one might expect to find a rain

shadow directly downstream of the mountains.

P732951-Ch08.qxd 9/12/05 7:47 PM Page 344

8.3 Deep Convection 345

The horizontal scale of deep convection is much

smaller than that of baroclinic waves, the timescale is

correspondingly shorter, and the aspect ratio (i.e., the

ratio of the characteristic depth scale D to the length

scale L) is much larger. As a consequence of the

different scaling, the Earth’s rotation plays only an

indirect role in the dynamics of deep convection,

the vertical motions are much stronger than in large-

scale motion, and hydrostatic balance does not always

prevail.

This section considers deep convection in its various

forms:

• individual convective cells consisting of a single

updraft and downdraft (this category includes

some thunderstorms);

• convective storms made up of organized groups

or sequences of convective cells; and

• mesoscale convective systems: bands or zones of

clouds and precipitation on a scale of 100 km or

larger in at least one direction that are generated

by interacting convective cells.

8.3.1 Environmental Controls

In idealized theoretical and modeling studies, deep

convection is viewed as developing within a large-

scale environment in which temperature, moisture,

and horizontal wind are horizontally uniform. The

vertical profiles of temperature and moisture in the

environment play a critical role in defining the

regions of the atmosphere in which deep convection

develops spontaneously, and the vertical wind profile

determines the direction and rate of movement of

convective storms and profoundly influences their

structure and evolution.

a. Temperature and moisture stratification

The necessary conditions for the occurrence of deep

convection are

• the existence of a conditionally unstable lapse

rate (i.e., 



)

• substantial boundary-layer moisture, and

• low level convergence (or lifting) sufficient to

release the instability.

Convection feeds on the potential energy inher-

ent in the temperature and moisture stratification.

The so-called convective available potential energy

(CAPE), (in J kg

1

) of a reference air parcel is

given by

(8.3)

where F is the upward buoyancy force per unit vol-

ume on the rising air parcel due to the temperature

difference between the parcel and its environment,





is the density of the air parcel, LFC is the level of

free convection, and EL is the equilibrium level

above which the parcel is no longer warmer than its

environment. By analogy with Exercise 3.11, it is

readily shown that the buoyancy force per unit mass

(F



) is given by (







)



times g, where



 is

the specific volume of the rising air parcel,



the specific volume of the environmental air at the

same level, and g is the gravitational acceleration.

Substituting for gdz from the hydrostatic equation

(3.18) and reversing the order of integration yield

Substituting from the equation of state (3.15) yields

(8.4)

If we ignore the small virtual temperature correction,

the integral in this expression is simply the area, on

the skew-T ln p plot, extending from LFC to EL and

bounded by the environmental temperature sound-

ing on the left and a moist adiabat on the right.

The reference air parcel used in computing the

CAPE may be an air parcel at the Earth’s surface or

it may be chosen to be representative of the mean

temperature and humidity of the air within the

boundary layer. As in the exercises in Chapter 3, the

parcel is lifted along a dry adiabat up to its lifting

condensation level (LCL) and then along a saturated

adiabat as illustrated in Fig. 8.42. The integration

begins at the LFC.

Exercise 8.1 Estimate the CAPE for a sounding in

which the LFC and EL for the reference air parcel

are 700 and 175 hPa, respectively, and within the

layer between those levels the reference air parcel is,

on average (with respect to ln p), 10 °C warmer than

the environmental air at the same level.

CAPE  R



LFC

(T

 T

)

d lnp

CAPE 



LFC

(aa) dp

CAPE 



LFC



r) dz

P732951-Ch08.qxd 9/12/05 7:47 PM Page 345

346 Weather Systems

Solution: Substituting values into (8.4), we obtain

For reference, values of CAPE ranging from 0 to

1000 J kg

1

are considered marginal for deep con-

vection, 1000–2500 adequate to support moderate

convection, 2500–4000 adequate to support strong

convection, and in excess of 4000 indicative of the

potential for extreme convection.

■

If it were a common occurrence for air parcels

in ordinary cumulus clouds to reach their level of free

convection, the CAPE would never build up to values

high enough to support vigorous deep convection.

Hence, the degree to which convection is inhibited by

the presence of a stable layer or inversion at the top

of the planetary boundary layer also plays a role in

setting the stage for convective storms. A measure

of this so-called convective inhibition (CIN or CINH)

is the energy, in units of J kg

1

, required to lift the

 3978 J kg

1

CAPE  287  10

C  ln(700



175)

reference air parcel to its LFC. So defined, CIN may

be viewed as negative CAPE and can be represented

as an area on a skew-T ln p plot, as shown in Fig. 8.42.

To set the stage for vigorous deep convection it is

essential that the CIN be non-zero, but not so large

that it precludes the possibility of deep convection

altogether. For CIN  100 J kg

1

, deep convection is

unlikely to occur in the absence of external forcing,

such as might be provided by daytime heating or the

approach of a strong front. A return of several thou-

sand units of CAPE on an investment of perhaps

several tens of units of “startup costs” required to

overcome the CIN rivals the performance of the most

successful new enterprises in the world of business!

The geographical distribution of the frequency of

lightning flashes shown in Fig. 6.56 provides a meas-

ure of the degree to which the vertical stratification

of temperature and moisture over various regions of

the world is conducive to deep convection. Many of

the features in this pattern mirror the distribution of

rainfall shown in Fig. 1.25. However, relative to the

rainfall, lightning flashes are relatively more frequent

over the continents than over the oceans because the

heating of the land surface greatly enhances the

CAPE during the afternoon hours, giving rise to

more vigorous convection.

For the CAPE inherent in the temperature and

moisture sounding to be realized, two things need to

happen: the environmental air needs to be destabi-

lized (i.e., the CIN needs to be reduced) by lifting

and, within this destabilized air mass, air parcels need

to be lifted up to their LFC. Lifting destabilizes the

environmental sounding by weakening the inversion

that caps the mixed layer so that buoyant air parcels

from below can break through it. This process is illus-

trated schematically in Fig. 8.43.

The lifting and associated low level convergence

that is responsible for lifting the inversion layer and

thereby destabilizing the environmental sounding is

usually associated with some large-scale forcing

mechanism such as the approach of an extratropical

cyclone, which can be anticipated a day or more in

advance on the basis of numerical weather prediction.

In contrast, the lifting of the air parcel that initiates

the deep convection is usually associated with a more

Another widely used indicator of the potential for deep convection is the so-called lifted index (LI), defined as the temperature

deficit (relative to the environment) of an air parcel originating at the earth’s surface that is lifted dry adiabatically up to its lifting conden-

sation level and then moist adiabatically up to the 500-hPa level. Negative lifted indices are indicative of a potential for deep convection;

values below 9 indicate the potential for severe convection. Variants of the lifted index based on air parcels originating at various heights

within the planetary boundary layer are also sometimes used.

100-

200-

300-

400-

500-

600-

700-

800-

900-

1000-

–20 –15 –10 –5 0 5 101520253035

LFC

LCL

CAPE

CIN

Fig. 8.42 A hypothetical sounding illustrating the concepts

of convective available potential energy (CAPE) and convec-

tive inhibition (CIN). The CAPE and CIN in this sounding are

indicated by shading.

P732951-Ch08.qxd 9/12/05 7:47 PM Page 346

8.3 Deep Convection 347

localized, short-lived and less predictable forcing

mechanism, such as a sea-breeze front, a range of

hills, or the leading edge of the outflow from a preex-

isting convective storm.

b. The vertical wind profile

Convective storms move at a speed approximately

equal to the vertically averaged horizontal wind in

their environment, where vertically averaged denotes a

mass (or pressure) weighted average over the depth of

the storm. Usually a mid-tropospheric steering level

can be identified at which the storm motion vector is

approximately equal to the wind in the storm’s envi-

ronment. However, it should be understood that the

storm is not really steered by the wind at any particu-

lar level: the steering level is simply the level at which

the wind vector most closely matches the layer-mean

wind vector. Under some conditions, storms propagate

systematically to the left or right of both the vertically

averaged wind and the wind at the steering level.

Convective storms often form in an environment

in which the vertical wind shear vector



V



z is

dominated by the increase in scalar wind speed V

with height. The strength of the shear affects the ver-

tical tilt of the updrafts and downdrafts within the

storm: weak shear favors a structure in which the

downdraft ultimately isolates the updraft from its

supply of low level moisture, leading to the storm’s

demise, while strong shear favors a tilted structure

with a symbiotic relationship between updraft and

downdraft, resulting in more intense, longer lived

storms capable of producing hail and strong winds.

Changes in wind direction with height also play

an important role in the dynamics of convective

storms. Vertical wind profiles that exhibit signifi-

cant veering and backing are conveniently dis-

played in terms of a hodograph: a plot of the wind

components u versus v for a single vertical sound-

ing, with the points representing successive levels

in the sounding connected by a curve. At any level

in the profile the vertical wind shear vector is

tangent to the hodograph curve at that level. In

both the idealized hodographs for a hypothetical

northern hemisphere station shown in Fig. 8.44,

the wind vector V is rotating clockwise (veering)

with height, but the veering is more pronounced

in panel (b). The straightness of hodograph in

Fig. 8.44a implies that the vertical wind shear

vector



V



z does not rotate with height (i.e., that

the shear is unidirectional). In contrast, the cur-

vature of the hodograph in Fig. 8.44b implies

that both V and



Vdz rotate with increasing

height. The importance of curved hodographs in

the dynamics of a class of convective storms called

supercells is touched on in Section 8.3.2.

In the presence of vertical wind shear, air pos-

sesses vorticity that can be visualized as a rolling

motion about a horizontal axis. For example, both

vertical profiles depicted in Fig. 8.44 exhibit vorticity,

in a clockwise sense, about the y axis. In analogy with

Table 7.1, the magnitude of the vorticity about the

y axis is (



u



z 



w



x), where s



u



zs is several

orders of magnitude larger thans



w



xs. Hence, the

vertical shear



u



z is, in effect, the vorticity about

the y axis.

Exercise 8.2 Compare the vorticity about a hori-

zontal axis due to a vertical wind shear of 3 m s

1

per

kilometer with the vorticity associated with the

Earth’s rotation.

Solution: The vorticity is equal to the shear, which is

3m s

1

or 3  10

3

1

. From Exercise 7.1 it can

Temperature T

Height z

Fig. 8.43 Illustration of the increase in the lapse rate dTdz

within an inversion layer as the layer is lifted. The black line seg-

ment AB represents the temperature profile within the inversion

layer before it is lifted; CD represents the temperature profile in

the same layer after it is lifted one height increment, EF after it

is lifted two height increments, etc. It is assumed that the bot-

tom of the layer is saturated with water vapor and cools at the

saturated adiabatic lapse rate as the layer is lifted, while the

top of the layer is unsaturated and cools at the dry adiabatic

lapse rate. The steepening of the lapse rate due to the differen-

tial rate of cooling is partially compensated by the expansion of

the air within the layer as it rises. This effect is not represented

in the diagram.

P732951-Ch08.qxd 9/12/05 7:47 PM Page 347

348 Weather Systems

be inferred that the vorticity associated with the Earth’s

rotation in the plane perpendicular to the axis of

rotation is .

Hence the vorticity inherent in this quite modest verti-

cal wind shear is about 20 times as large as the vorticity

associated with the Earth’s rotation. ■

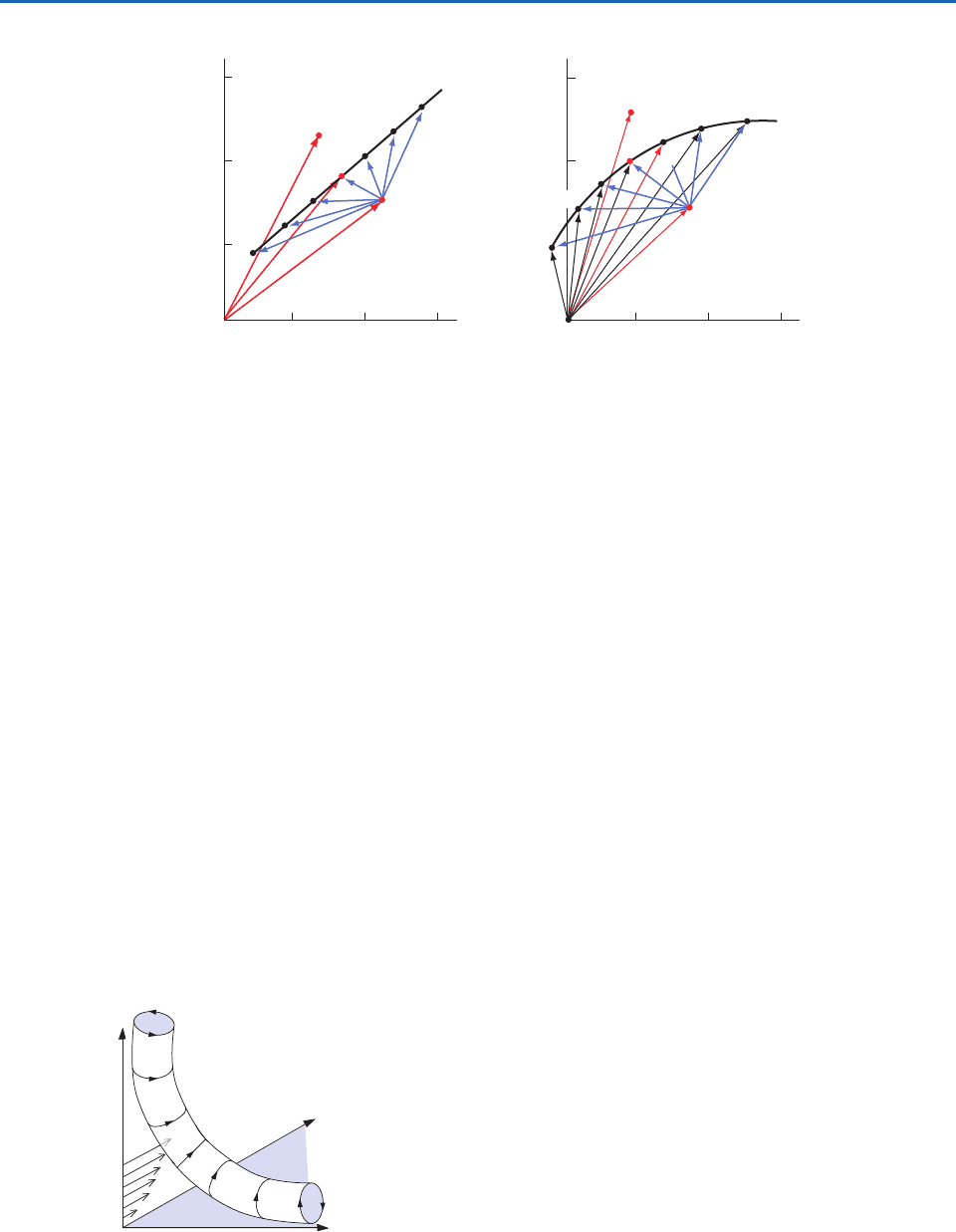
When boundary layer air is drawn into the updraft

of a convective storm, the vorticity about a horizontal

axis may be tilted so that it is transformed into vortic-

ity about a vertical axis, as illustrated in Fig. 8.45. In

this schematic the wind, the vertical wind shear, and

the storm movement are all envisioned as being in the

x direction and the updraft of the storm is centered

22  7.29  10

5

1

 1.5  10

4

over the y axis. Note how counterclockwise vorticity

about the x axis (as viewed looking in the positive

direction along the axis) is tilted into counterclockwise

vorticity about the z axis, as viewed from above.This is

a powerful mechanism for imparting rotation to con-

vective storms.

c. Geographic regions susceptible

to convective storms

During springtime, the central United States enjoys

the dubious distinction of experiencing more tornadic

thunderstorms than any region of comparable size in

the world. Storms break out in the warm sectors of

extratropical cyclones, where all the essential ingredi-

ents are present:

• convectively unstable soundings characterized

by warm, humid, boundary-layer air flowing

northward from the Gulf of Mexico, capped by

dry, conditionally unstable air flowing eastward

from the Rockies;

• strong vertical wind shear, as evidenced by the

presence of a jet stream at the 250-hPa level;

• strong veering of the wind with height, with

southerly low flow underlying westerly flow

aloft; and

• strong synoptic-scale lifting associated with the

passage of cyclones and their associated fronts.

Fig. 8.44 Idealized northern hemisphere vertical wind profiles depicted in the form of hodographs. Points on the hodograph

indicate the ends of wind vectors radiating out from the origin. The points are numbered in order from the bottom to the top

of the profiles, which extend from the ground up to the tropopause. Both profiles exhibit veering of the wind with height. In

(a) the vertical wind shear Vz is unidirectional, while in (b) it rotates clockwise with height, as indicated by the curvature of

the hodograph. In both panels a midtropospheric steering level S and velocity vectors for hypothetical storms moving toward the

left L and right R of the steering flow are indicated in red. The sense of the curvature of the hodograph determines whether left-

or right-moving storms are favored, as explained in the next subsection. Light blue arrows show the relative flow in a coordinate

system moving with the right-moving storm.

10 20 300

v (m s

–1

)

(a)

10 20 300

u (m s

–1

)

(b)

v (m s

–1

)

u (m s

–1

)

Fig. 8.45 Schematic showing how the updraft of a con-

vective storm can acquire vorticity about a vertical axis by

ingesting boundary layer air that possesses vorticity about

the x axis by virtue of the vertical shear u z. See text for

further explanation.

P732951-Ch08.qxd 9/12/05 7:47 PM Page 348

8.3 Deep Convection 349

8.3.2 Structure and Evolution

of Convective Storms

Weather-related deaths and injuries, property dam-

age and transportation disruptions occur much more

frequently in association with localized convective

storms than with extratropical cyclones: so much so,

in fact, that the terms severe storm and severe weather

are implicitly understood as applying to convective

storms, unless otherwise specified.

A great deal has been learned about the structure

and dynamics of convective storms during the past

few decades. Dual-Doppler analysis

has made it

possible to map the three-dimensional wind field in

the updrafts and downdrafts of storms that are too

intense to probe safely with research aircraft. Using

numerical models, it has been possible to simulate

many of the observed structural features of convec-

tive storms and to determine the types of storms that

are favored in various large-scale environments. This

section presents a brief synopsis of these results.

Thunderstorms are made up of cells, which develop,

mature, and decay, as illustrated in Fig. 8.46. The

left panel shows young, rapidly growing cells in the

foreground, fueled by midtropospheric CAPE, with

deeper, more fully developed cells in the background.

The top of the cell at the upper right is approaching its

equilibrium level, beyond which rising air parcels are

no longer buoyant, so they spread out to form an

anvil. The right panel shows a fully developed anvil,

which is still being fed by new convective cells rising

out of the boundary layer.

Most human fatalities attributable to convective storms are caused by lightning, which is an everyday occurrence during certain sea-

sons in some parts of the world. In an average year 50 lightning-related deaths occur in the United States, with highest rates per capita in

the Rocky Mountain states and Florida, where lightning occurs most frequently. An overwhelming percentage of lightning deaths involve

males. Hail is the major source of property damage. In a typical year over the United States hail causes two to three times as much prop-

erty damage as tornadoes. The highest frequency of occurrence of damaging hail is over the western Great Plains, where it causes annual

crop losses amounting to 5% of total crop value. Slow-moving convective storms are capable of producing flash floods, characterized by

abrupt rises in water levels in rivers and streams, that may pose a serious threat to life and property downstream. Winds that form in an

environment with strong vertical wind shear are often accompanied by damaging winds, as described in the next subsection.

Analysis of radial velocity measurements from two or more Doppler radars to determine the three-dimensional velocity field in a

region of precipitation.

Most of the ground-based photographs shown in this section were provided by amateur or professional meteorologists who maintain

or share Web sites: www.stormeffects.com (Brian Morganti); www.twisterchasers.com (Kathryn Piotrowski); www.mesoscale.ws (Eric

Nguyen); skydiary.com (Chris Kridler); and www.dblanchard.net (David Blanchard). These sites provide numerous additional examples of

observed convective storms and related phenomena.

Fig. 8.46 Deep convective cells in various stages in the development of a tornadic storm near Anthony, Kansas, May 25, 1997.

The photo in the left panel was taken about an hour and a half before sunset, looking eastward. The photo in the right panel

was taken around sunset, looking eastward toward the departing storm. [Courtesy of Brian Morganti.

]

P732951-Ch08.qxd 9/12/05 7:47 PM Page 349

350 Weather Systems

Convective storms can be classified as

• relatively small, benign, single cell storms that

form under conditions of weak vertical wind

shear;

• more dangerous multicell storms that develop

under conditions of strong vertical wind shear;

and

• intense, robust, long-lived supercell storms with

rotating updrafts formed from the splitting of

multicell storms.

Both multi- and supercell storms are capable of

producing hail and strong winds. Most damaging

tornadoes are associated with supercell storms.

a. Ordinary thunderstorms

The term airmass thunderstorm or simply ordinary

thunderstorm is used to describe small isolated

cumulonimbus clouds (Fig. 8.47) produced by local

convection in an unstable airmass rather than by

fronts or instability lines. These systems generally

develop just one main precipitation shower (a single

cell storm), and the pressure field is entirely deter-

mined by buoyancy of the warm updraft.

Ordinary thunderstorms were the subject of an

intensive field program, known as the Thunderstorm

Project, which was carried out over Florida and Ohio

during the late 1940s. Data on a large number of

storms were composited together to construct an ide-

alized model of the life cycle of a typical single-cell

thunderstorms. In this model, which is depicted in

Fig. 8.48, the life cycle of a single cell within a multi-

cell storm is shown in terms of three stages: cumulus,

mature, and dissipating. Multicell storms consist of

several such cells, which grow and decay in succes-

sion, each having a lifetime of about half an hour.

In the cumulus stage (Fig. 8.48a) the cloud consists

entirely of a warm, buoyant plume of rising air. The

updraft velocity increases rapidly with height within the

cloud and there is considerable entrainment through

the lateral cloud boundaries. The top of the cloud

moves upward with a velocity of up to 10 m s

1

Because of the large updraft velocities, supercooled

raindrops may be present well above the freezing level

(a situation potentially hazardous to aircraft because of

the possibility of icing). The mature stage (Fig. 8.48b)

is characterized by the development of a vigorous

downdraft circulation, which coincides with the region

of heaviest rain.

The downdraft circulation is initiated by the down-

ward drag force induced by the drops. Dry environ-

mental air entrained into the downdraft (on the

right-hand side of Fig. 8.48b) and unsaturated air

below cloud base are cooled by evaporation of

falling precipitation. In some cases the resulting

evaporative cooling is capable of greatly enhancing

the negative buoyancy of the downdraft air. In the

mature stage, supercooled raindrops still exist well

above the freezing level in the updraft, while

snowflakes or soft hail pellets may be found below

the freezing level in the downdraft. The maximum

updraft vertical velocities are in the middle of the

cloud, with detrainment above that level. The top of

the cloud approaches the tropopause and begins to

spread out horizontally as an anvil in the dissipating

stage (Fig. 8.48c). As precipitation develops through-

out the cloud, the downdraft circulation gradually

becomes more extensive until, in the dissipating

stage, it occupies virtually the entire cloud. Deprived

of a source of supersaturated updraft air, cloud

droplets can no longer grow and, as a consequence,

precipitation soon ceases. Only about 20% of the

water vapor condensed in the updraft actually

reaches the ground in the form of precipitation. The

remainder evaporates in the downdraft or is left

Fig. 8.47 A small isolated cumulonimbus cloud. [Courtesy

of Art Rangno.]

P732951-Ch08.qxd 9/12/05 7:47 PM Page 350

8.3 Deep Convection 351

behind as cloud debris (including extensive patches

of anvil cirrus), to evaporate into the ambient air.

The single-cell thunderstorm is short lived and

rarely produces destructive winds or hail because it

contains a built in “self-destruct mechanism” namely,

the downdraft circulation induced by the rainshaft

(Fig. 8.48c). In the absence of vertical wind shear the

thunderstorm has no way of ridding itself of the pre-

cipitation it produces without destroying the buoyant

updrafts that feed it.

b. Multicell storms

Multicell storms are characterized by a succession of

cells, each evolving through its own cycle as in a sin-

gle cell storm and, in the process, promoting the

development of new cells. Under conditions of weak

vertical wind shear, the storms tend to be poorly

organized and the relationship between the individ-

ual cells so weak as to be barely discernible.

However, when the shear is strong, the individual

cells may be so tightly integrated that they lose their

own identity to the larger scale andor longer lived

entity of which they are a part. The mode of organi-

zation of multicell storms also depends on the parti-

tioning of the shear between the components aligned

with and transverse to the wind itself. A prominent

feature of many convective storms is the gust front,

where warm, moist boundary-layer air is lifted by the

leading edge of the evaporatively cooled (and there-

fore relatively dense) air diverging from the base of

the downdraft. New cells tend to form along the

advancing gust front, sustaining the multicell storm,

while older cells die out as they fall behind the gust

front and become surrounded by cooler, denser

downdraft air.

A schematic of an idealized symmetric multicell

storm is shown in Fig. 8.49 in coordinates moving

with the storm. New convective cells are shown form-

ing in the air that is lifted by the approaching gust

front. When air lifted by the gust front reaches its

level of free convection, it begins to rise sponta-

neously under the force of its own buoyancy. Water

vapor condenses onto cloud droplets and ice parti-

cles in the updraft and, when the particles grow suffi-

ciently heavy, their fall speeds exceed the updraft

velocity and they fall out. Dry environmental air,

with low equivalent potential temperature is shown

entering the storm from the rear at middle levels. As

precipitation particles fall out of the updraft into this

dry air, they partially evaporate and, in so doing, they

cool the air toward its wet bulb temperature. As the

air cools it becomes negatively buoyant relative to its

surroundings and begins to sink. The frictional drag

of the falling precipitation particles produces an

additional downward force, intensifying the down-

draft. The updraft air is shown exiting the storm on

the downwind side, forming an anvil that may extend

100 km or more in advance of the storm. Hence, from

the perspective of a ground-based observer, the pas-

sage of this storm would be marked by thickening

high overcast, followed by the approach of a much

❄

❄ ❄

❄

Pressure (hPa)

Height (km)

(c)(b)(a)

250–

500–

700–

–40°C

Rain

Snow

Ice

Wind vector scale

0 5 10 m s

–1

0°C

SURFACE

–5

–10

Fig. 8.48 Schematic of a typical ordinary single-cell thunderstorm in three stages of its life cycle showing (a) cumulus stage,

(b) mature stage, and (c) dissipating stage. The horizontal scale is compressed by about 30% relative to the vertical scale in the figure.

The 0 °C and 40 °C isotherms are indicated in red. [Adapted from The Thunderstorm, U.S. Government Printing Office (1949).]

P732951-Ch08.qxd 9/12/05 7:47 PM Page 351

352 Weather Systems

lower, darker cloud base, followed by an abrupt wind

shift and temperature drop that marks the arrival of

the gust front. Heavy precipitation would not begin

until a few minutes after the passage of the gust front

and might include hail. The shallow pool of cool,

moistened downdraft air left behind by the storm

may persist for hours, inhibiting the development of

further convection.

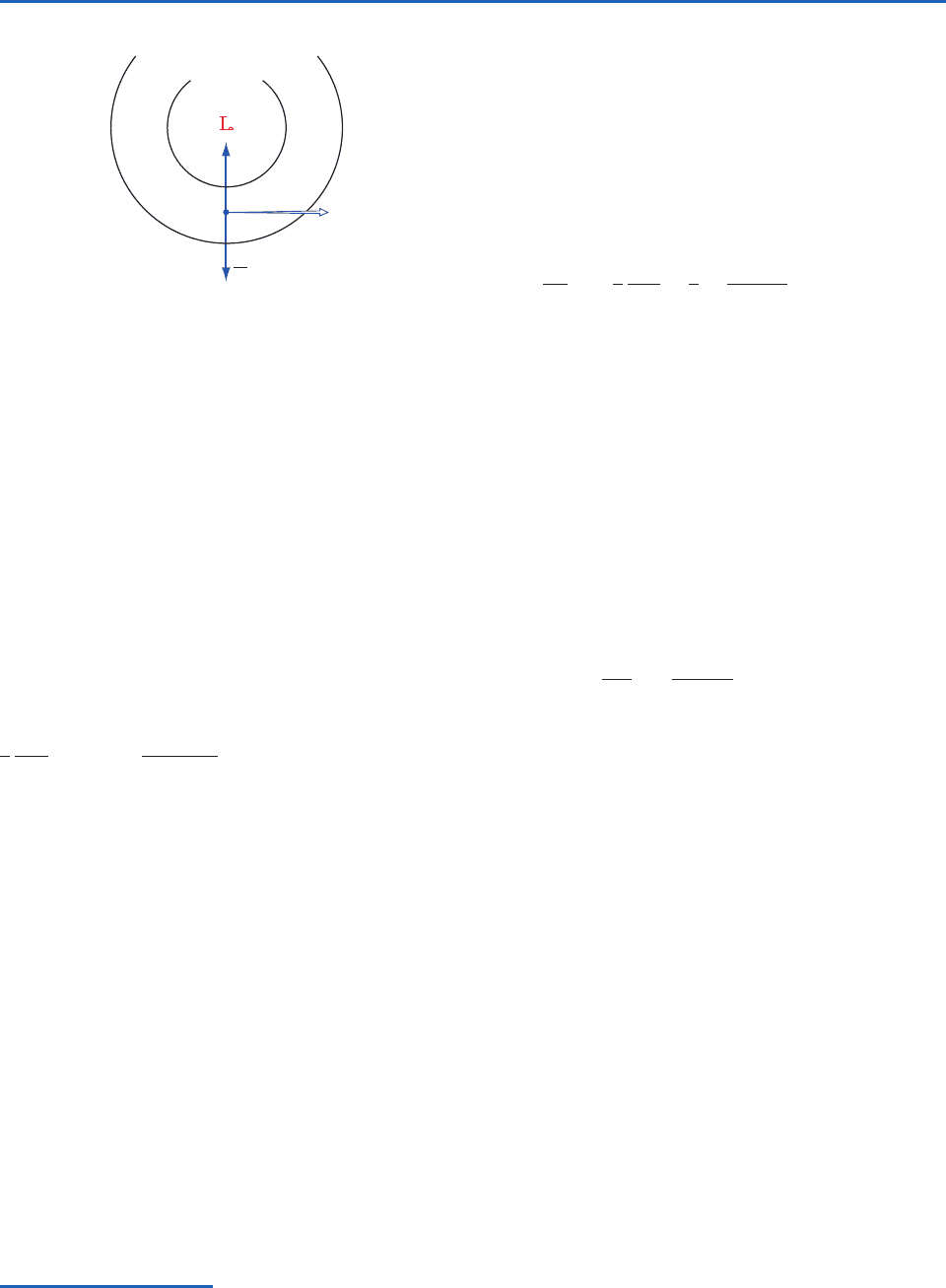
c. Supercell storms

The distinguishing characteristic of the supercell

storm is its rotating updraft that is clearly evident in

Fig. 8.50, and even more so in time-lapse photo-

graphs and in dual-Doppler radar imagery. Rotation

renders the supercell storm more robust by inducing

the formation of a mesolow (i.e., a pressure mini-

mum) within the updraft, which is superimposed

upon the hydrostatically balanced pressure field that

exists by virtue of the density gradients. The mesolow

forms as the rotating air is pulled outward from the

center of the updraft by the centrifugal force.

Pressure at the center of the updraft drops until the

inward-directed pressure gradient force and the

outward-directed centrifugal force come into in a

state of cyclostrophic balance, as illustrated schemati-

cally in Fig. 8.51. Under these conditions,

(8.5)

where



is the speed of the air circulating around the

updraft at radius r.









Fig. 8.49 Schematic of an idealized multicell storm developing in an environment with strong vertical shear in the direction of

the vertically averaged wind. The vertical profile of equivalent potential temperature



in the environment is shown at the left,

together with the wind profile. Arrows in the right panel denote motion relative to the moving storm.

02040

320 340

(K)

u(m s

–1

)

(a) (b)

Rain shaft

Gust front

Moist layer

Inversion

New cells

Mamma

Anvil

Tropopause

"Overshooting"

cloud top

Storm motion

125

250

500

1000

Height (km)

Pressure (hPa)

(c)

Direction of motion

Geostrophic balance and cyclostrophic balance are special cases of the more general, three-way gradient wind balance discussed in

Section 7.2.7. In the case of geostrophic balance, the centrifugal force is neglected, while in the case of cyclostrophic balance the Coriolis

force is neglected. Which forces need to be retained and which ones can be neglected depend on whether the vorticity of the system under

consideration is much smaller than, comparable to, or much larger than the planetary vorticity; for the specific case of circular vortices, it

depends on the rotation rate, as shown in Exercise 8.9. In contrast to flow that is in geostrophic balance, cyclostrophic flow can circulate in

either direction around a mesolow and, indeed, both clockwise and counterclockwise circulations have been observed.

Fig. 8.50 Supercell thunderstorm over north-central Kansas

on May 8, 2001, with a rotating updraft and a shaft of heavy

rain and hail. [Courtesy of Chris Kridler.]

P732951-Ch08.qxd 9/12/05 7:47 PM Page 352

8.3 Deep Convection 353

Exercise 8.3 Air at cloud base in a supercell

updraft is observed to be in solid body rotation out

to a radius of 2 km with a period of 15 minutes.

Estimate the amplitude of the dynamically-induced

radial pressure gradient. The density of the air at

cloud base is 1 kg m

3

Solution: Let p

be the dynamically induced pres-

sure perturbation (in Pa), r the radius, and



the

rotation rate.Assuming cyclostrophic balance,

Multiplying by the density of the air, we obtain

p

r  0.1 Pa m

1

 1 hPa km

1

. ■

The intensity of a dynamically induced mesolow is

thus proportional to the square of the rotation rate,

which tends to be small at the Earth’s surface, but

increases rapidly with height in the lower part of the

updraft. Hence the dynamically induced pressure

deficit 



at the center of the updraft amplifies

with height, giving rise to a hydrostatically unbal-

anced, upward-directed pressure gradient force

(1



)p

z below the updraft, which reenforces the

upward acceleration of the air beneath the updraft. It

is this dynamic (nonhydrostatic) contribution to the

three-dimensional pressure distribution that renders

super-cell storms more intense and longer lasting

than ordinary thunderstorm cells.









r 





15  60s



 2  10

m  0.1 m s

2

Exercise 8.4 Estimate the magnitude of the upward

acceleration at the base of the updraft due to the

presence of a dynamically induced pressure pertur-

bation p

that increases from zero at the ground to

1 hPa at an altitude of 1 km above the ground. The

density of the air is 1 kg m

3

Solution:

Over an interval of 1 min, a force of this magnitude

would impart a vertical velocity of 6 m s

1

to the air

beneath the updraft.The importance of the dynamically

induced pressure gradient force in maintaining the up-

draft is further illustrated in the following exercise. ■

Exercise 8.5 How large a temperature perturbation

would be required to impart a hydrostatically bal-

anced vertical acceleration equivalent to that in the

previous exercise?

Solution: In Exercise 3.11 it was shown that

where T is the perturbed temperature. Substituting



 1kgm

3

and and solving for TT,

we obtain a value of 3 °C.

■

How do supercell storms acquire their rotation? To

answer this question, consider a storm developing in

an environment in which wind speed is increasing with

height, but without any turning of the wind with

height. Suppose that an isolated, deep convective

updraft develops in this environment and that it ini-

tially moves downstream with the vertically averaged

steering flow. Boundary layer air is blowing into the

updraft from the right and left flanks as well as from

the front, as shown in the top panel of Fig. 8.52. As in

the schematic shown in Fig. 8.45, the low level air flow-

ing into the right flank of the updraft exhibits counter-

clockwise vorticity as viewed looking toward the left.

As imaginary tubes of this inflow air bend upward

into the right side of the updraft, they spin in a coun-

terclockwise sense (looking downward). By the same

T  288 K







TT

 0.1 ms

2











100 Pa

1000 m

 0.1 m s

2

This value is an overestimate because the pressure perturbation induced by the rotation of the air in the updraft extends downward,

with reduced amplitude, all the way to the ground. The horizontal pressure gradient force due to the presence of the mesolow at the

ground strengthens the low level horizontal inflow into the updraft.

Fig. 8.51 Balance of forces in flow that is in a state of

cyclostrophic balance. P denotes the pressure gradient force,

V the horizontal wind vector, V the scalar wind speed, and R

the radius of curvature.

P732951-Ch08.qxd 9/12/05 7:47 PM Page 353