Воробьев М.С. Устройства генерирования радиосигналов

41

ɬɟɪɶ ɡɚ ɫɱɟɬ ɤɨɧɟɱɧɨɝɨ ɜɪɟɦɟɧɢ ɜɨɫɫɬɚ-

ɧɨɜɥɟɧɢɹ ɡɚɤɪɵɬɨɝɨ ɫɨɫɬɨɹɧɢɹ ɩɟɪɟ-

ɯɨɞɚ; Ʉ — ɤɥɸɱ, ɢɦɢɬɢɪɭɸɳɢɣ ɨɬɤɪɵ-

ɬɢɟ ɢ ɡɚɤɪɵɬɢɟ ɩɟɪɟɯɨɞɚ. ɉɪɢ ɷɬɨɦ

R

ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɜɪɟɦɟɧɢ ɪɟɤɨɦɛɢ-

ɧɚɰɢɢ ɧɟɨɫɧɨɜɧɵɯ ɧɨɫɢɬɟɥɟɣ

τ

ɪ

;

r

ɩɪɨ-

ɩɨɪɰɢɨɧɚɥɶɧɨ ɜɪɟɦɟɧɢ ɜɨɫɫɬɚɧɨɜɥɟɧɢɹ

τ

ɜ

; L, C

ɤ

ɨɛɵɱɧɨ ɫɱɢɬɚɸɬ ɱɚɫɬɶɸ

ɜɧɟɲɧɟɣ ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɞɢɨɞɭ ɰɟɩɢ.

ɂɡ ɫɯɟɦɵ ɧɚ ɪɢɫ. 4.4, ɚ ɫɥɟɞɭɟɬ, ɱɬɨ ɫɭɳɟɫɬɜɭɟɬ ɤɨɧɟɱɧɚɹ ɨɛɥɚɫɬɶ ɱɚɫɬɨɬ,

ɜ ɩɪɟɞɟɥɚɯ ɤɨɬɨɪɨɣ ɜɚɪɚɤɬɨɪ ɦɨɠɧɨ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɤɚɤ ɩɪɟɢɦɭɳɟɫɬɜɟɧɧɨ ɧɟɥɢ-

ɧɟɣɧɭɸ ɟɦɤɨɫɬɶ ɢ ɝɞɟ ɩɪɢ ɭɦɧɨɠɟɧɢɢ ɱɚɫɬɨɬɵ ɭɪɨɜɟɧɶ ɩɨɬɟɪɶ ɦɟɧɶɲɟ ɞɨ-

ɩɭɫɬɢɦɨɝɨ. ȼ ɪɟɠɢɦɟ ɡɚɩɟɪɬɨɝɨ ɩɟɪɟɯɨɞɚ ɩɨɬɟɪɢ ɜ ɜɚɪɚɤɬɨɪɟ ɡɚɜɢɫɹɬ ɬɨɥɶɤɨ ɨɬ

R

s

ɢ ɞɢɨɞ ɦɨɠɧɨ ɯɚɪɚɤɬɟɪɢɡɨɜɚɬɶ ɞɨɛɪɨɬɧɨɫɬɶɸ

( )

Sɉ

RUC

Q

n

ω

1

=

,

ɝɞɟ

C

ɩ

(U

ɉ

)

— ɺɦɤɨɫɬɶ ɩɟɪɟɯɨɞɚ ɩɪɢ ɫɬɚɧɞɚɪɬɧɨɦ ɫɦɟɳɟɧɢɢ

u = U

ɉ

,

ɭɤɚɡɚɧɧɨɦ ɜ ɩɚɫɩɨɪɬɟ ɞɢɨɞɚ. ɋ ɭɜɟɥɢɱɟɧɢɟɦ ɱɚɫɬɨɬɵ ɞɨɛɪɨɬɧɨɫɬɶ ɩɚɞɚɟɬ.

ɑɚɫɬɨɬɚ, ɧɚ ɤɨɬɨɪɨɣ ɞɨɛɪɨɬɧɨɫɬɶ ɪɚɜɧɚ ɟɞɢɧɢɰɟ, ɧɚɡɵɜɚɟɬɫɹ ɩɪɟɞɟɥɶɧɨɣ

ɱɚɫɬɨɬɨɣ ɭɦɧɨɠɟɧɢɹ:

( )

Sɉ

RUC

f

n

ɩɪɟɞ

π

2

1

=

. (4.5)

Ⱦɥɹ ɨɛɟɫɩɟɱɟɧɢɹ ɞɨɫɬɚɬɨɱɧɨ ɛɨɥɶɲɨɣ ɞɨɛɪɨɬɧɨɫɬɢ ɭɦɧɨɠɢɬɟɥɹ ɩɪɢɧɢɦɚɸɬ

N

f

1

≤ (0,05...0,1)

f

ɩɪɟɞ

. Ⱦɥɹ ɫɟɪɢɣɧɨ ɜɵɩɭɫɤɚɟɦɵɯ ɚɪɫɟɧɢɞ-ɝɚɥɥɢɟɜɵɯ ɜɚɪɚɤɬɨɪɨɜ

ɩɪɟɞɟɥɶɧɵɟ ɱɚɫɬɨɬɵ ɫɨɫɬɚɜɥɹɸɬ 100…300 ȽȽɰ, ɩɨɷɬɨɦɭ ɦɚɤɫɢɦɚɥɶɧɵɟ ɱɚɫɬɨɬɵ

ɜɵɯɨɞɧɨɝɨ ɫɢɝɧɚɥɚ ɞɥɹ ɧɢɯ ɪɚɜɧɵ ɩɪɢɦɟɪɧɨ 10-25 ȽȽɰ.

ȼ ɭɦɧɨɠɢɬɟɥɟ ɧɚ ɜɚɪɚɤɬɨɪɚɯ ɜɨɡɦɨɠɧɚ ɪɚɛɨɬɚ ɜ ɪɟɠɢɦɟ ɫ ɱɚɫɬɢɱɧɵɦ

ɨɬɩɢɪɚɧɢɟɦ ɩɟɪɟɯɨɞɚ, ɬ.ɟ. ɩɪɢ

u

< 0, ɟɫɥɢ ɜɪɟɦɹ, ɧɚ ɤɨɬɨɪɨɟ ɩɟɪɟɯɨɞ ɨɬɩɢɪɚɟɬɫɹ

ɦɟɧɶɲɟ, ɱɟɦ ɫɪɟɞɧɟɟ ɜɪɟɦɹ ɪɟɤɨɦɛɢɧɚɰɢɢ ɧɟɨɫɧɨɜɧɵɯ ɧɨɫɢɬɟɥɟɣ ɡɚɪɹɞɚ ɜ ɛɚɡɟ.

ɋ ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ, ɞɥɢɬɟɥɶɧɨɫɬɶ ɩɟɪɢɨɞɚ ɤɨɥɟɛɚɧɢɣ ɞɨɥɠɧɚ ɛɵɬɶ ɦɧɨɝɨ ɛɨɥɶɲɟ

ɜɪɟɦɟɧɢ ɜɨɫɫɬɚɧɨɜɥɟɧɢɹ ɡɚɤɪɵɬɨɝɨ ɫɨɫɬɨɹɧɢɹ ɩɟɪɟɯɨɞɚ. ȿɫɥɢ ɜɜɟɫɬɢ ɩɨɧɹɬɢɟ

ɞɨɛɪɨɬɧɨɫɬɢ ɩɨ ɪɟɤɨɦɛɢɧɚɰɢɨɧɧɵɦ

Q

ɪ

ɢ ɢɧɟɪɰɢɨɧɧɵɦ

Q

ɜ

ɩɨɬɟɪɹɦ

Q

ɜ

ɪ,

,=

1

ω τ

ɬɨ ɝɪɚɧɢɱɧɵɟ ɱɚɫɬɨɬɵ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ, ɩɪɢɪɚɜɧɢɜɚɹ ɷɬɢ ɞɨɛɪɨɬɧɨɫɬɢ

ɟɞɢɧɢɰɟ :

f f

ɧ ɜ ɜ

=

1 2 1 2( ); ( ),

ɪ

π

τ

π

τ

(4.6)

ɢ ɭɫɥɨɜɢɟ ɦɚɥɨɫɬɢ ɩɨɬɟɪɶ ɜɵɩɨɥɧɹɟɬɫɹ ɜ ɞɢɚɩɚɡɨɧɟ ɱɚɫɬɨɬ

f

ɧ

< f < f

ɜ

.

L R

s

Ʉ

R C

C

ɤ

C

ɩ

(u)

R

s

C

ɞ

r

ɚ) ɛ)

Ɋɢɫ. 4.4. ɗɤɜɢɜɚɥɟɧɬɧɵɟ ɫɯɟɦɵ

ɜɚɪɚɤɬɨɪɚ

42

4.5

Ⱥɧɚɥɢɡ ɭɦɧɨɠɢɬɟɥɹ ɱɚɫɬɨɬɵ ɩɚɪɚɥɥɟɥɶɧɨɝɨ ɬɢɩɚ

1 Ⱥɧɚɥɢɡ ɪɚɛɨɬɵ ɭɦɧɨɠɢɬɟɥɹ ɜ ɪɟɠɢɦɟ ɫ ɱɚɫɬɢɱɧɵɦ ɨɬɩɢɪɚɧɢɟɦ

ɩɟɪɟɯɨɞɚ. ȼ ɷɬɨɦ ɪɟɠɢɦɟ ɜ ɬɟɱɟɧɢɟ ɱɚɫɬɢ ɩɟɪɢɨɞɚ ɞɢɨɞ ɨɬɤɪɵɬ ɢ ɟɝɨ ɺɦɤɨɫɬɶ ɜ

ɷɬɨɬ ɢɧɬɟɪɜɚɥ ɜɪɟɦɟɧɢ ɪɚɜɧɚ ɞɢɮɮɭɡɢɨɧɧɨɣ ɺɦɤɨɫɬɢ. Ɉɛɵɱɧɨ ɫɱɢɬɚɸɬ, ɱɬɨ ɨɧɚ

ɛɟɫɤɨɧɟɱɧɨ ɜɟɥɢɤɚ, ɩɨɷɬɨɦɭ ɡɚɜɢɫɢɦɨɫɬɶ ɫɭɦɦɚɪɧɨɣ ɺɦɤɨɫɬɢ ɩɟɪɟɯɨɞɚ ɩɪɟɞ-

ɫɬɚɜɥɹɸɬ ɜ ɜɢɞɟ

( )

(

)

(

)







≤∞

>

=

.0 ɩɪɢ

;0 ɩɪɢ

00

u

uuUUC

uC

ɩ

γ

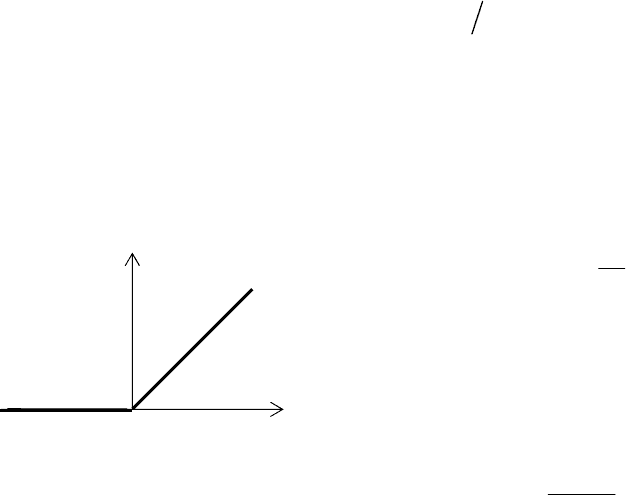
Ʉɚɤ ɩɪɚɜɢɥɨ, ɞɥɹ ɷɬɨɝɨ ɪɟɠɢɦɚ ɢɫɩɨɥɶɡɭɸɬɫɹ ɞɢɨɞɵ ɫ ɩɥɚɜɧɵɦ ɩɟɪɟɯɨɞɨɦ.

ɉɨɷɬɨɦɭ ɫ ɰɟɥɶɸ ɭɩɪɨɳɟɧɢɹ ɚɧɚɥɢɡɚ ɩɪɟɧɟɛɪɟɝɚɸɬ ɡɚɜɢɫɢɦɨɫɬɶɸ ɺɦɤɨɫɬɢ

ɡɚɩɟɪɬɨɝɨ p-n ɩɟɪɟɯɨɞɚ. Ɂɚɜɢɫɢɦɨɫɬɶ ɧɚɩɪɹɠɟɧɢɹ ɧɚ ɩɟɪɟɯɨɞɟ ɨɬ ɡɚɪɹɞɚ ɜ

ɫɭɦɦɚɪɧɨɣ ɺɦɤɨɫɬɢ ɩɪɢɨɛɪɟɬɚɟɬ ɜɢɞ (ɪɢɫ. 4.5)











<

≥

=

,0ɩɪɢ0

;0ɩɪɢ

q

C

q

u

ɝɞɟ

C

— ɧɟɤɨɬɨɪɚɹ ɭɫɪɟɞɧɟɧɧɚɹ ɟɦɤɨɫɬɶ ɡɚ-

ɩɟɪɬɨɝɨ ɞɢɨɞɚ, ɤɨɬɨɪɭɸ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ,

ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:

(

)

ɩɪɨɛ

UCC

ɩ

γ

−

=

2

, (4.7)

ɝɞɟ

C

ɜ

(U

ɩɪɨɛ

)

— ɺɦɤɨɫɬɶ ɜɚɪɚɤɬɨɪɚ ɩɪɢ ɧɚɩɪɹɠɟɧɢɢ ɩɪɨɛɨɹ.

ɉɨɫɤɨɥɶɤɭ ɜ ɩɚɪɚɥɥɟɥɶɧɨɣ ɫɯɟɦɟ ɱɟɪɟɡ ɞɢɨɞ ɩɪɨɬɟɤɚɸɬ ɬɨɥɶɤɨ ɞɜɟ ɝɚɪɦɨ-

ɧɢɱɟɫɤɢɟ ɫɨɫɬɚɜɥɹɸɳɢɟ ɬɨɤɚ, ɬɨ ɡɚɪɹɞ ɺɦɤɨɫɬɢ ɩɟɪɟɯɨɞɚ ɛɭɞɟɬ ɢɦɟɬɶ ɜɢɞ

q (t)=q

0

+ q

1

⋅

cos

ω

1

t + q

N

⋅

cos(N

⋅ω

1

t+

ϕ

N

),

(4.8)

ϕ

N

— ɮɚɡɚ ɤɨɥɟɛɚɧɢɣ ɡɚɪɹɞɚ ɫ ɱɚɫɬɨɬɨɣ

N

⋅ω

1

. ȼɟɥɢɱɢɧɚ

ϕ

N

ɞɨɥɠɧɚ ɛɵɬɶ

ɜɩɨɥɧɟ ɨɩɪɟɞɟɥɟɧɧɨɣ ɞɥɹ ɨɛɟɫɩɟɱɟɧɢɹ ɧɚɢɛɨɥɟɟ ɷɮɮɟɤɬɢɜɧɨɝɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ.

ȿɫɥɢ ɷɬɨɬ ɭɝɨɥ ɫɞɟɥɚɬɶ ɪɚɜɧɵɦ

ϕ

N

=

k

π

(

k

= 0, 1, 2, ...), ɬɨ ɮɚɡɵ ɝɚɪɦɨɧɢɱɟɫɤɢɯ

ɫɨɫɬɚɜɥɹɸɳɢɯ ɧɚɩɪɹɠɟɧɢɹ ɧɚ ɩɟɪɟɯɨɞɟ

u = q/C

ɢ ɮɚɡɵ ɝɚɪɦɨɧɢɱɟɫɤɢɯ

ɫɨɫɬɚɜɥɹɸɳɢɯ ɬɨɤɚ ɱɟɪɟɡ ɞɢɨɞ

i = dq/dt

ɛɭɞɭɬ ɫɞɜɢɧɭɬɵ ɧɚ ɭɝɨɥ

π

/2

ɨɬɧɨɫɢɬɟɥɶɧɨ ɞɪɭɝ ɞɪɭɝɚ. ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɜɵɯɨɞɧɚɹ ɦɨɳɧɨɫɬɶ

P

N

= 0.

ɇɚɩɪɨɬɢɜ, ɞɥɹ ɩɨɥɭɱɟɧɢɹ ɦɚɤɫɢɦɚɥɶɧɨɣ ɜɵɯɨɞɧɨɣ ɦɨɳɧɨɫɬɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ

ɝɚɪɦɨɧɢɤɢ ɬɨɤɚ ɢ ɧɚɩɪɹɠɟɧɢɹ ɞɨɥɠɧɵ ɛɵɬɶ ɜ ɮɚɡɟ, ɱɬɨ ɩɨɥɭɱɚɟɬɫɹ ɩɪɢ

ϕ

N

=

π

/2

ɗɬɨ ɨɛɟɫɩɟɱɢɜɚɟɬɫɹ ɧɚɫɬɪɨɣɤɨɣ ɜɵɯɨɞɧɨɝɨ ɤɨɧɬɭɪɚ ɭɦɧɨɠɢɬɟɥɹ. ɉɨɷɬɨɦɭ

ɜɵɪɚɠɟɧɢɟ (4.8) ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ

q(t)=q

0

+ q

1

⋅

cos

ω

1

t

−

q

N

⋅

sin(N

⋅ω

1

t).

(4.8)

ȼɜɟɞɺɦ ɩɨɧɹɬɢɟ ɭɝɥɚ ɨɬɫɟɱɤɢ

θ

, ɯɚɪɚɤɬɟɪɢɡɭɸɳɟɝɨ ɱɚɫɬɶ ɩɟɪɢɨɞɚ ɤɨɥɟ-

ɛɚɧɢɣ, ɜ ɬɟɱɟɧɢɟ ɤɨɬɨɪɨɝɨ ɩɟɪɟɯɨɞ ɡɚɤɪɵɬ. Ɇɨɦɟɧɬɵ ɨɬɤɪɵɬɢɹ ɢ ɡɚɤɪɵɬɢɹ

u

q

Ɋɢɫ. 4.5. Ɂɚɜɢɫɢɦɨɫɬɶ ɧɚɩɪɹ-

ɠɟɧɢɹ ɧɚ ɩɟɪɟɯɨɞɟ ɨɬ ɡɚɪɹɞɚ

43

ɨɩɪɟɞɟɥɹɸɬɫɹ ɭɫɥɨɜɢɟɦ

q

= 0. ɗɬɢ ɦɨɦɟɧɬɵ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɛɟɡ ɭɱɟɬɚ

ɫɨɫɬɚɜɥɹɸɳɟɣ

q

N

, ɟɫɥɢ ɧɚɥɨɠɟɧɨ ɨɝɪɚɧɢɱɟɧɢɟ

K

q

q N

N

= ≤

1

sin

,

Θ

ɤɨɬɨɪɨɟ ɦɨɠɧɨ ɨɛɟɫɩɟɱɢɬɶ ɩɨɞɛɨɪɨɦ

R

ɧ

. ɍɝɨɥ ɨɬɫɟɱɤɢ ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɨɩɪɟ-

ɞɟɥɹɟɬɫɹ ɤɚɤ

cos .

Θ

=

−

q q

0 1

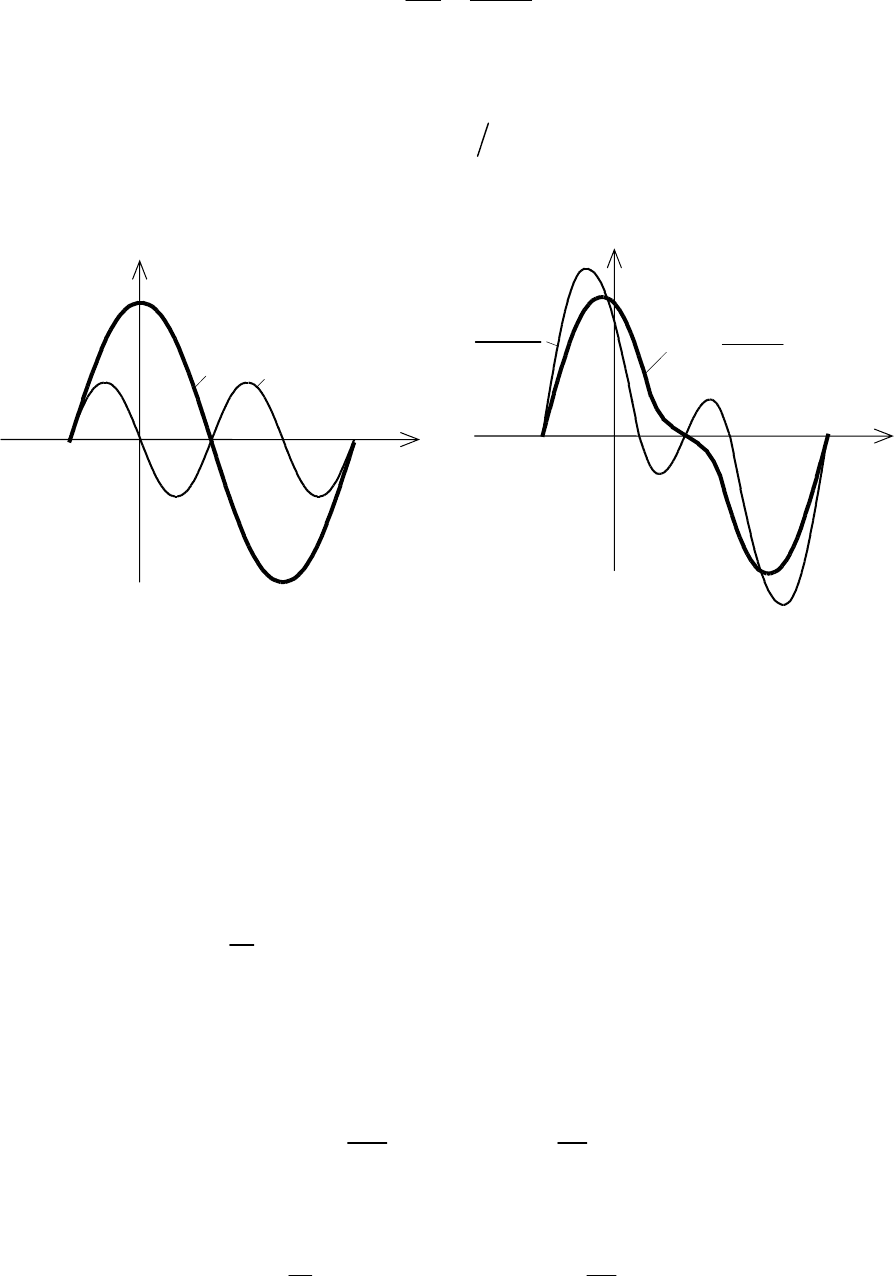
ɉɪɨɞɟɦɨɧɫɬɪɢɪɭɟɦ ɷɬɨ ɧɚ ɩɪɢɦɟɪɟ ɭɞɜɨɢɬɟɥɹ ɱɚɫɬɨɬɵ ɫ

Θ

= 90

ɨ

. ȼ ɷɬɨɦ

ɫɥɭɱɚɟ

q

0

= 0, ɢ ɮɨɪɦɚ ɡɚɪɹɞɚ ɧɚ ɩɟɪɟɯɨɞɟ ɢɦɟɟɬ ɜɢɞ, ɩɨɤɚɡɚɧɧɵɣ ɧɚ ɪɢɫ. 4.6.

q

1

,q

N

q

1

+q

N

q

1

q

N

K

N

>

sin

Θ

K

N

≤

sin

Θ

ω

t

ω

t

Ɋɢɫ. 4.6. ȼɪɟɦɟɧɧɵɟ ɡɚɜɢɫɢɦɨɫɬɢ ɡɚɪɹɞɨɜ ɺɦɤɨɫɬɢ ɩɟɪɟɯɨɞɚ

ɜɚɪɚɤɬɨɪɚ ɩɪɢ N = 2

ɂɡ ɩɨɫɬɪɨɟɧɢɣ ɜɢɞɧɨ, ɩɪɢ ɨɝɪɚɧɢɱɟɧɢɢ (4.9) ɦɨɦɟɧɬɵ ɩɟɪɟɯɨɞɚ ɡɧɚɱɟɧɢɹ

ɫɭɦɦɚɪɧɨɝɨ ɡɚɪɹɞɚ

q

ɱɟɪɟɡ ɧɨɥɶ ɫɨɜɩɚɞɚɸɬ ɫ ɦɨɦɟɧɬɚɦɢ ɩɟɪɟɯɨɞɚ ɱɟɪɟɡ ɧɨɥɶ

ɡɚɪɹɞɚ

q

1

. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɡɚɪɹɞɚ ɦɨɠɧɨ ɫ ɭɱɟɬɨɦ (4.10)

ɡɚɩɢɫɚɬɶ ɜ ɫɥɟɞɭɸɳɟɦ ɜɢɞɟ:

q(t)= q

1

⋅

cos(

ω

1

t

−

cos

Θ

)

−

q

N

⋅sin(N

⋅ω

1

t).

(4.11)

ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɩɟɪɟɯɨɞɟ ɪɚɜɧɨ

u

C

q t q N t

N

= − −

1

1 1 1

[ (cos cos ) sin( )]

ω ωΘ

ɩɪɢ

−Θ +2π

k <

ω

1

t <

Θ +2π

k

,

k

= 0, 1, 2, ...; ɢ

u=

0 ɜɨ ɜɫɺ ɨɫɬɚɥɶɧɨɟ ɜɪɟɦɹ.

Ɋɚɡɥɨɠɢɦ ɧɚɩɪɹɠɟɧɢɟ

u(t)

ɜ ɪɹɞ Ɏɭɪɶɟ. Ⱦɥɹ ɷɬɨɝɨ ɪɚɫɫɱɢɬɚɟɦ ɚɦɩɥɢɬɭɞɵ

ɝɚɪɦɨɧɢɤ ɪɹɞɚ. ɉɨɫɬɨɹɧɧɚɹ ɫɨɫɬɚɜɥɹɸɳɚɹ ɪɚɜɧɚ

( )

Ĭ

C

q

dtuU

Ĭ

0

1

10

)(

2

1

γω

π



−

==

. (4.13)

Ⱥɦɩɥɢɬɭɞɵ ɤɨɫɢɧɭɫɨɢɞɚɥɶɧɵɯ ɝɚɪɦɨɧɢɤ ɪɚɜɧɵ

( )

Ĭ

C

q

dtktuU

k

Ĭ

ck

γωω

π



−

==

1

11

cos)(

1

. (4.14)

(4.9)

(4.10)

(4.12)

44

Ⱥɦɩɥɢɬɭɞɵ ɫɢɧɭɫɨɢɞɚɥɶɧɵɯ ɝɚɪɦɨɧɢɤ ɪɚɜɧɵ

(

)

(

)













+

−

−==



−

kN

ĬkN

kN

ĬkN

C

q

dtktuU

Ĭ

sk

sinsin1

sin)(

1

11

π

ωω

π

.

Ⱦɥɹ ɢɧɬɟɪɟɫɭɸɳɢɯ ɧɚɫ ɝɚɪɦɨɧɢɤ

k

= 1 ɢ

k = N

ɢɦɟɟɦ

( )













−−=−=

N

NĬ

Ĭ

C

q

UĬN

C

q

U

N

sN

s

2

2sin1

;

1

π

γ

. (4.15)

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɨɥɭɱɢɥɢ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɪɚɛɨɱɢɯ ɝɚɪɦɨɧɢɤ ɧɚɩɪɹɠɟɧɢɹ ɧɚ

ɩɟɪɟɯɨɞɟ

u(t) = U

0

+ U

c1

cos

ω

1

t + U

cN

cosN

ω

1

t + U

s1

sin

ω

1

t + U

sN

sinN

ω

1

t.

ɋɪɚɜɧɢɦ ɷɬɨ ɜɵɪɚɠɟɧɢɟ ɫ ɜɵɪɚɠɟɧɢɟɦ ɬɨɤɚ ɱɟɪɟɡ ɞɢɨɞ:

i t

dq

dt

I t I N t

N

( ) sin sin ,= = − −

1 1 1

ω ω

ɝɞɟ

I

1

= q

1

ω

1

,

I

N

= q

N

ω

1

.

ɋ ɭɱɟɬɨɦ ɡɧɚɤɨɜ ɤɨɷɮɮɢɰɢɟɧɬɨɜ ɪɹɞɚ Ɏɭɪɶɟ ɦɨɠɧɨ ɫɞɟɥɚɬɶ ɫɥɟɞɭɸɳɢɟ

ɜɵɜɨɞɵ.

• ɇɚ ɩɟɪɟɯɨɞɟ ɩɪɢɫɭɬɫɬɜɭɟɬ ɩɨɫɬɨɹɧɧɨɟ ɧɚɩɪɹɠɟɧɢɟ

U

0

.

• ȼɬɨɪɨɣ ɱɥɟɧ ɫɭɦɦɵ

u(t)

ɧɚɯɨɞɢɬɫɹ ɜ ɤɜɚɞɪɚɬɭɪɟ ɫ ɩɟɪɜɨɣ ɝɚɪɦɨɧɢɤɨɣ ɬɨɤɚ

I

1

. ɗɬɨ ɷɤɜɢɜɚɥɟɧɬɧɨ ɬɨɦɭ, ɱɬɨ ɬɨɤ

I

1

ɩɪɨɬɟɤɚɟɬ ɩɨ ɧɟɤɨɬɨɪɨɣ ɺɦɤɨɫɬɢ

C

q

U

C

ɷ

c

1

1 1

= =

γ

( )

.

Θ

• ɑɟɬɜɟɪɬɵɣ ɱɥɟɧ ɫɭɦɦɵ

u(t)

ɧɚɯɨɞɢɬɫɹ ɜ ɮɚɡɟ ɫ ɩɟɪɜɨɣ ɝɚɪɦɨɧɢɤɨɣ ɬɨɤɚ ɢ

ɨɩɪɟɞɟɥɹɟɬ ɚɤɬɢɜɧɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ

R

U

I

q

N

C

ɷ

s N N

1

1 1 1

= = ⋅

⋅

γ

ω

( )

.

Θ

• ɑɟɬɜɟɪɬɵɣ ɱɥɟɧ ɫɭɦɦɵ

u(t)

— ɧɚɩɪɹɠɟɧɢɟ, ɤɨɥɟɛɥɸɳɟɟɫɹ ɫ ɱɚɫɬɨɬɨɣ

N

ω

1

, ɧɚɯɨɞɢɬɫɹ ɜ ɩɪɨɬɢɜɨɮɚɡɟ ɫ N-ɣ ɝɚɪɦɨɧɢɤɨɣ ɬɨɤɚ

I

N

. ɋɥɟɞɨɜɚɬɟɥɶɧɨ,

ɷɬɨ ɧɚɩɪɹɠɟɧɢɟ ɟɫɬɶ ɷ.ɞ.ɫ.

e N

q

C

N

( ) ( ).

ω γ

1

=

Θ

• ɇɚɤɨɧɟɰ, ɩɹɬɵɣ ɱɥɟɧ ɫɭɦɦɵ

u(t)

— ɧɚɩɪɹɠɟɧɢɟ, ɤɨɥɟɛɥɸɳɟɟɫɹ ɫ ɱɚɫɬɨɬɨɣ

N

ω

1

, ɧɚɯɨɞɢɬɫɹ ɜ ɤɜɚɞɪɚɬɭɪɟ ɫ N-ɣ ɝɚɪɦɨɧɢɤɨɣ ɬɨɤɚ

I

N

ɢ ɨɩɪɟɞɟɥɹɟɬ ɷɤɜɢ-

ɜɚɥɟɧɬɧɭɸ ɜɵɯɨɞɧɭɸ ɺɦɤɨɫɬɶ

Ĭ

C

N

NĬ

Ĭ

C

Nɗ

π

≈

¸

¹

·

¨

©

§

−

=

2

2sin1

. (4.18)

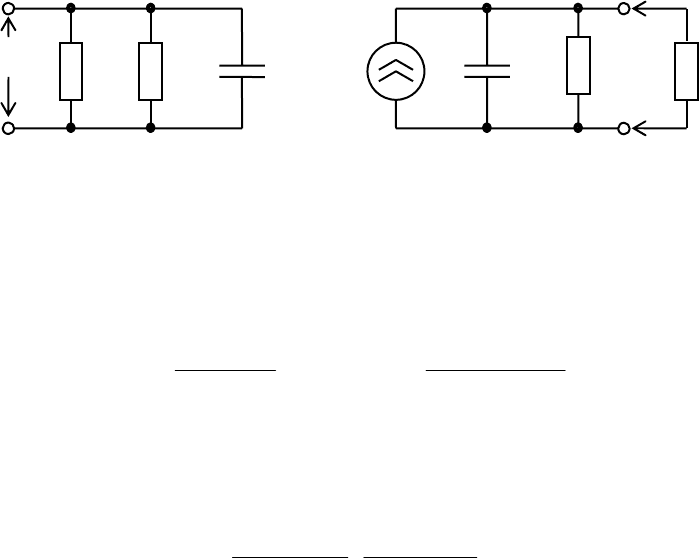
ȼɫɟ ɷɬɨ ɩɨɡɜɨɥɹɟɬ ɫɨɫɬɚɜɢɬɶ ɷɤɜɢɜɚɥɟɧɬɧɭɸ ɫɯɟɦɭ ɞɢɨɞɚ, ɪɚɛɨɬɚɸɳɟɝɨ ɜ

ɫɨɫɬɚɜɟ ɭɦɧɨɠɢɬɟɥɹ ɱɚɫɬɨɬɵ (ɪɢɫ. 4.7). ɋɯɟɦɚ ɭɦɧɨɠɢɬɟɥɹ ɪɚɡɛɢɥɚɫɶ ɧɚ ɞɜɚ

(4.16)

(4.17)

45

ɤɨɧɬɭɪɚ: ɜɯɨɞɧɨɣ ɢ ɜɵɯɨɞɧɨɣ. Ɍɚɤɢɟ ɫɯɟɦɵ ɭɦɧɨɠɢɬɟɥɟɣ ɩɨɥɭɱɢɥɢ ɧɚɡɜɚɧɢɟ

ɞɜɭɯɤɨɧɬɭɪɧɵɯ.

R

s

C

1ɷ

C

Nɷ

R

s

jX

ɧ

Z

ɜɯ

R

1ɷ

e(N

ω

1

) R

ɧ

Ɋɢɫ. 4.7. ɗɤɜɢɜɚɥɟɧɬɧɚɹ ɫɯɟɦɚ ɜɚɪɚɤɬɨɪɚ ɜ ɭɦɧɨɠɢɬɟɥɟ ɱɚɫɬɨɬɵ

ɗɤɜɢɜɚɥɟɧɬɧɚɹ ɫɯɟɦɚ ɜɚɪɚɤɬɨɪɚ ɩɨɡɜɨɥɹɟɬ ɪɚɫɫɱɢɬɚɬɶ ɨɫɧɨɜɧɵɟ ɩɚɪɚɦɟɬɪɵ

ɭɦɧɨɠɢɬɟɥɹ: ɜɵɯɨɞɧɭɸ ɦɨɳɧɨɫɬɶ

P

N

ɢ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ

η

.

Ɇɨɳɧɨɫɬɶ, ɩɨɞɜɟɞɟɧɧɚɹ ɤ ɞɢɨɞɭ,

P I R R P P

s ɷ s ɩ1 1

2

1 1

0 5= ⋅ + = +, ( ) ,

ɪ

ɝɞɟ

P

1s

— ɦɨɳɧɨɫɬɶ ɪɚɫɫɟɹɧɧɚɹ ɜ

R

s

;

P

ɩɪ

— ɦɨɳɧɨɫɬɶ, ɩɟɪɟɞɚɧɧɚɹ ɜɨ ɜɬɨɪɨɣ

ɤɨɧɬɭɪ. ɉɪɟɨɛɪɚɡɨɜɚɧɧɚɹ ɦɨɳɧɨɫɬɶ

P

P R

R R

ɩ

ɷ

s ɷ

ɪ

.=

⋅

+

1 1

1

Ɇɨɳɧɨɫɬɶ

P

ɩɪ

, ɜ ɫɜɨɸ ɨɱɟɪɟɞɶ, ɬɚɤɠɟ ɱɚɫɬɢɱɧɨ ɪɚɫɫɟɢɜɚɟɬɫɹ ɜ

R

s

(ɡɚ ɫɱɟɬ

ɩɪɨɬɟɤɚɧɢɹ ɬɨɤɚ

I

N

), ɚ ɱɚɫɬɢɱɧɨ ɩɟɪɟɞɚɟɬɫɹ ɜ ɧɚɝɪɭɡɤɭ:

P

P R

R R

P

R

R R

R

R R

ɧ

ɩ ɧ

s ɧ

ɷ

s ɷ

ɧ

s ɧ

=

⋅

+

=

+

⋅

+

ɪ

. .

1

Ɉɬɫɸɞɚ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ

η

=

+

⋅

+

R

R R

R

R R

ɷ

s ɷ

ɧ

s ɧ

1

.

ɂɡ ɜɵɪɚɠɟɧɢɹ (4.17) ɦɨɠɧɨ ɢɫɤɥɸɱɢɬɶ ɧɟɢɡɜɟɫɬɧɵɟ ɜɟɥɢɱɢɧɵ

q

1

ɢ

q

N

.

ȿɫɥɢ ɜɵɯɨɞɧɚɹ ɰɟɩɶ ɫɨɝɥɚɫɨɜɚɧɚ, ɬɨ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜɵɪɚɠɟɧɢɟ

e N

I

q

q N C

R R

N N

N

ɧ s

( ) ( )

,

ω

γ

ω

1 1

1

= ⋅ = +

Θ

ɢ ɧɚɣɬɢ ɢɡ ɧɟɝɨ ɨɬɧɨɲɟɧɢɟ ɡɚɪɹɞɨɜ

q

q N C R R

N N

ɧ s1 1

=

+

γ

ω

( )

.

Θ

ɉɨɞɫɬɚɜɥɹɹ ɷɬɨ ɜɵɪɚɠɟɧɢɟ ɜ (4.17), ɧɚɯɨɞɢɦ

R

C R R

ɷ

N

ɧ s

1

2

1

2 2

=

+

γ

ω

( )

.

Θ

(4.19)

(4.20)

(4.21)

(4.22)

46

Ⱦɥɹ ɡɚɜɟɪɲɟɧɢɹ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɪɚɫɱɟɬɚ ɧɟɨɛɯɨɞɢɦɨ ɧɚɣɬɢ ɧɚɩɪɹ-

ɠɟɧɢɟ ɫɦɟɳɟɧɢɹ. ɇɚɣɞɟɦ ɜɟɥɢɱɢɧɭ ɡɚɪɹɞɚ

q

N

ɢɡ ɜɵɯɨɞɧɨɣ ɦɨɳɧɨɫɬɢ

P

I R q N R

q

P

R N

N

N ɧ N ɧ

N

ɧ

= = =

2 2 2

1

2

1

2 2

2 1

ω

, .

ɬ.ɟ.

Ɉɬɫɸɞɚ, ɢɫɩɨɥɶɡɭɹ ɜɵɪɚɠɟɧɢɹ (4.13) ɢ (4.21), ɧɚɯɨɞɢɦ

U

P

R

R R

N

ɧ

ɧ s0

0

2

= +

γ

( )

( ).

Θ

2. Ⱥɧɚɥɢɡ ɪɚɛɨɬɵ ɭɦɧɨɠɢɬɟɥɹ ɜ ɪɟɠɢɦɟ ɩɨɥɧɨɝɨ ɡɚɩɢɪɚɧɢɹ ɩɟɪɟɯɨɞɚ.

ȼ ɷɬɨɦ ɪɟɠɢɦɟ ɧɟɨɛɯɨɞɢɦɨ ɭɱɢɬɵɜɚɬɶ ɫɬɪɨɝɭɸ ɡɚɜɢɫɢɦɨɫɬɶ ɦɟɠɞɭ ɡɚɪɹɞɨɦ

ɺɦɤɨɫɬɢ ɩɟɪɟɯɨɞɚ ɢ ɧɚɩɪɹɠɟɧɢɟɦ ɧɚ ɧɟɦ:

( )



=

u

duuCq

0

.

ɉɨɞɫɬɚɜɥɹɹ ɫɸɞɚ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɟɦɤɨɫɬɢ (4.4), ɩɨɫɥɟ ɢɧɬɟɝɪɢɪɨɜɚɧɢɹ ɧɚɯɨɞɢɦ

γ

−

==



1

00

0

00

1

u

UC

du

u

UC

q

u

,

ɝɞɟ

C

0

= C(U

0

)

— ɺɦɤɨɫɬɶ ɩɟɪɟɯɨɞɚ ɩɪɢ ɧɚɩɪɹɠɟɧɢɢ ɫɦɟɳɟɧɢɹ

U

0

. Ɍɚɤɢɦ

ɨɛɪɚɡɨɦ, ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɩɟɪɟɯɨɞɟ

γ

−

¸

¹

·

¨

©

§

−

=

1

00

1

q

UC

u

.

ɉɪɟɞɫɬɚɜɢɦ ɡɚɪɹɞ

q

ɜ ɜɢɞɟ ɫɭɦɦɵ ɩɨɫɬɨɹɧɧɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ

q

0

, ɨɛɪɚɡɭɸɳɟɣɫɹ

ɡɚ ɫɱɟɬ ɩɨɫɬɨɹɧɧɨɝɨ ɫɦɟɳɟɧɢɹ

U

0

, ɢ ɩɟɪɟɦɟɧɧɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ

q

ɩ

:

q

=

q

0

+

q

ɩ

.

ɉɨɫɬɨɹɧɧɭɸ ɫɨɫɬɚɜɥɹɸɳɭɸ ɥɟɝɤɨ ɨɩɪɟɞɟɥɢɬɶ ɢɡ (4.25):

q U

C U

0 0

1

( ) .=

−

γ

ȼ ɩɚɪɚɥɥɟɥɶɧɨɣ ɫɯɟɦɟ ɬɨɤ ɱɟɪɟɡ ɞɢɨɞ ɫɨɞɟɪɠɢɬ ɞɜɟ ɝɚɪɦɨɧɢɤɢ:

i I t I N t

N N

=

+

1 1 1

cos cos( ),

ω

ϕ

ɝɞɟ

ϕ

N

— ɮɚɡɚ N-ɣ ɝɚɪɦɨɧɢɤɢ ɬɨɤɚ ɨɬɧɨɫɢɬɟɥɶɧɨ ɩɟɪɜɨɣ. ɉɟɪɟɦɟɧɧɚɹ ɫɨɫ-

ɬɚɜɥɹɸɳɚɹ ɡɚɪɹɞɚ ɧɚɯɨɞɢɬɫɹ ɢɡ (4.28):



= dtiq

n

.

ɉɨɞɫɬɚɜɥɹɹ (4.28) ɜ (4.29) ɢ ɭɱɢɬɵɜɚɹ (4.27), ɦɨɠɧɨ (2.26) ɩɟɪɟɩɢɫɚɬɶ ɜ

ɜɢɞɟ

(4.23)

(4.24)

(4.25)

(4.26)

(4.27)

(4.28)

(4.29)

47

γγ

γ

−−

−

¸

¹

·

¨

©

§

+=













+=













−

=

1

0

1

0

1

0

1

00

1

0

1)(

)1(

q

Uqq

q

U

q

UC

U

u

n

. (4.30)

Ⱦɥɹ

γ

= 1/2 (ɫɥɭɱɚɣ ɪɟɡɤɨɝɨ ɩɟɪɟɯɨɞɚ) ɜɵɪɚɠɟɧɢɟ (4.30) ɢɦɟɟɬ ɤɨɧɟɱɧɨɟ ɱɢɫɥɨ

ɱɥɟɧɨɜ ɢ ɥɟɝɤɨ ɩɨɞɞɚɟɬɫɹ ɚɧɚɥɢɡɭ. Ⱦɥɹ ɩɥɚɜɧɨɝɨ ɩɟɪɟɯɨɞɚ

γ

= 1/3 ɹɜɧɨɟ

ɜɵɪɚɠɟɧɢɟ ɩɨɥɭɱɢɬɶ ɧɟɥɶɡɹ, ɢ ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɢɫɩɨɥɶɡɭɸɬ ɩɪɢɛɥɢɠɟɧɧɨɟ ɪɟɲɟ-

ɧɢɟ. Ɍɚɤ ɤɚɤ

q

ɩ

/q

0

≤ 1, ɬɨ ɜɵɪɚɠɟɧɢɟ ɜ ɫɤɨɛɤɚɯ ɜ (4.30) ɦɨɠɧɨ ɪɚɡɥɨɠɢɬɶ ɜ

Ɇɚɤɥɨɪɟɧɚ. ɉɨɫɥɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ, ɟɫɥɢ ɨɬɛɪɨɫɢɬɶ ɦɚɥɵɟ ɱɥɟɧɵ ɢ ɧɟɪɚɛɨɱɢɟ

ɝɚɪɦɨɧɢɤɢ, ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɜɵɪɚɠɟɧɢɟ, ɫɨɞɟɪɠɚɳɢɟ ɩɹɬɶ ɱɥɟɧɨɜ, ɤɚɤ ɢ ɜ ɪɟ-

ɠɢɦɟ ɫ ɱɚɫɬɢɱɧɵɦ ɨɬɩɢɪɚɧɢɟɦ ɩɟɪɟɯɨɞɚ:

u=U

′

0

+ U

c1

sin

ω

1

t + U

cN

sin(N

ω

1

t+

ϕ

N

) +

+U

a1

cos[

ω

1

t+

ϕ

N

–0,5(N – 2)

π

] – U

aN

cos[N

ω

1

t + 0,5(N – 2)

π

].

(4.31)

ɉɟɪɜɵɣ ɱɥɟɧ ɩɪɚɜɨɣ ɱɚɫɬɢ (4.31) — ɷɬɨ ɧɚɩɪɹɠɟɧɢɟ ɫɦɟɳɟɧɢɹ ɞɢɨɞɚ. Ɂɚɦɟɬɢɦ,

ɱɬɨ

U

′

0

≠

U

0

. ɇɚɩɪɹɠɟɧɢɟ ɫɦɟɳɟɧɢɹ ɧɟɦɧɨɝɨ ɭɜɟɥɢɱɢɜɚɟɬɫɹ ɡɚ ɫɱɟɬ

ɜɵɩɪɹɦɥɹɸɳɟɝɨ ɞɟɣɫɬɜɢɹ ɧɟɥɢɧɟɣɧɨɣ ɺɦɤɨɫɬɢ, ɱɬɨ ɩɪɢɜɨɞɢɬ ɤ ɩɪɨɬɟɤɚɧɢɸ

ɧɟɛɨɥɶɲɨɝɨ ɩɨɫɬɨɹɧɧɨɝɨ ɬɨɤɚ ɱɟɪɟɡ ɞɢɨɞ.

ȼɬɨɪɨɣ ɢ ɬɪɟɬɢɣ ɱɥɟɧɵ ɜɵɪɚɠɟɧɢɹ (4.31) ɩɪɟɞɫɬɚɜɥɹɸɬ ɫɨɛɨɣ ɝɚɪɦɨɧɢɱɟɫɤɢɟ

ɤɨɥɟɛɚɧɢɹ ɩɟɪɜɨɣ ɢ n-ɣ ɝɚɪɦɨɧɢɤ, ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ, ɢ ɧɚɯɨɞɹɬɫɹ ɜ ɤɜɚɞɪɚɬɭɪɟ ɤ

ɝɚɪɦɨɧɢɤɚɦ ɬɨɤɚ. ɗɬɢ ɱɥɟɧɵ ɨɩɪɟɞɟɥɹɸɬ ɷɤɜɢɜɚɥɟɧɬɧɵɟ ɜɯɨɞɧɭɸ

C

1ɷ

ɢ

ɜɵɯɨɞɧɭɸ

C

Nɷ

ɺɦɤɨɫɬɢ. Ⱦɥɹ ɢɧɠɟɧɟɪɧɵɯ ɪɚɫɱɟɬɨɜ ɦɨɠɧɨ ɩɪɢɧɹɬɶ

C

1ɷ

≈

C

Nɷ

≈

C

0

. (4.32)

ȿɫɥɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɣ ɧɚɫɬɪɨɣɤɨɣ ɜɵɯɨɞɧɨɣ ɰɟɩɢ ɭɦɧɨɠɢɬɟɥɹ ɨɛɟɫɩɟɱɢɬɶ

ɮɚɡɭ ɧɚɝɪɭɡɤɢ

ϕ

N

= 0,5(N – 2)

π

,

ɬɨ ɱɟɬɜɟɪɬɵɣ ɱɥɟɧ ɜɵɪɚɠɟɧɢɹ (4.31) ɛɭɞɟɬ

ɧɚɯɨɞɢɬɶɫɹ ɜ ɮɚɡɟ ɫ ɜɯɨɞɧɵɦ ɬɨɤɨɦ

I

1

. ɗɬɨ ɨɡɧɚɱɚɟɬ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɷɧɟɪɝɢɢ,

ɱɬɨ ɦɨɠɧɨ ɨɬɪɚɡɢɬɶ ɫ ɩɨɦɨɳɶɸ ɷɤɜɢɜɚɥɟɧɬɧɨɝɨ ɚɤɬɢɜɧɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ

R

U

I

ɷ

a

1

= .

ɉɹɬɵɣ ɱɥɟɧ ɜɵɪɚɠɟɧɢɹ (4.31) ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɜɵɪɚɠɚɟɬ ɷ.ɞ.ɫ., ɨɛɟɫɩɟɱɢɜɚɸɳɭɸ

ɩɪɨɬɟɤɚɧɢɟ ɬɨɤɚ N-ɣ ɝɚɪɦɨɧɢɤɢ ɜ ɜɵɯɨɞɧɵɯ ɰɟɩɹɯ ɭɦɧɨɠɢɬɟɥɹ.

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɵ ɩɪɢɲɥɢ ɤ ɬɨɣ ɠɟ ɞɜɭɯɤɨɧɬɭɪɧɨɣ ɷɤɜɢɜɚɥɟɧɬɧɨɣ ɫɯɟɦɟ,

ɱɬɨ ɢ ɜ ɪɟɠɢɦɟ ɫ ɱɚɫɬɢɱɧɵɦ ɨɬɩɢɪɚɧɢɟɦ ɩɟɪɟɯɨɞɚ (ɪɢɫ. 4.7). ɋɥɟɞɨɜɚɬɟɥɶɧɨ,

ɫɩɪɚɜɟɞɥɢɜɨ ɢ ɜɵɪɚɠɟɧɢɟ (4.20) ɞɥɹ ɤɨɷɮɮɢɰɢɟɧɬɚ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ.

ɋɞɟɥɚɟɦ ɞɜɚ ɡɚɦɟɱɚɧɢɹ ɨɬɧɨɫɢɬɟɥɶɧɨ ɩɪɢɦɟɧɟɧɢɹ ɮɨɪɦɭɥɵ (4.20).

1. ȼɟɥɢɱɢɧɚ ɷɤɜɢɜɚɥɟɧɬɧɨɝɨ ɫɨɩɪɨɬɢɜɥɟɧɢɹ

R

1ɷ

ɛɭɞɟɬ ɡɚɜɢɫɟɬɶ ɨɬ ɜɟɥɢ-

ɱɢɧɵ ɬɨɤɨɜ

I

1

ɢ

I

N

. ɉɨɷɬɨɦɭ ɭɦɧɨɠɢɬɟɥɶ, ɧɚɫɬɪɨɟɧɧɵɣ ɩɪɢ ɨɞɧɨɣ ɜɯɨɞɧɨɣ

ɦɨɳɧɨɫɬɢ, ɛɭɞɟɬ ɪɚɫɫɬɪɨɟɧ ɩɪɢ ɞɪɭɝɨɣ ɟɺ ɜɟɥɢɱɢɧɟ.

48

2. ɋɭɳɟɫɬɜɭɟɬ ɧɟɤɨɬɨɪɚɹ ɨɩɬɢɦɚɥɶɧɚɹ ɜɟɥɢɱɢɧɚ ɧɚɝɪɭɡɤɢ

R

ɧ

, ɩɪɢ ɤɨɬɨɪɨɣ

ɦɚɤɫɢɦɚɥɟɧ ɤɨɷɮɮɢɰɢɟɧɬ

η

ɢɥɢ ɦɚɤɫɢɦɚɥɶɧɚ ɜɵɯɨɞɧɚɹ ɦɨɳɧɨɫɬɶ. ɉɪɢɱɟɦ ɷɬɢ

ɷɤɫɬɪɟɦɭɦɵ ɧɟ ɫɨɜɩɚɞɚɸɬ.

4.6. Ⱥɧɚɥɢɡ ɭɦɧɨɠɢɬɟɥɹ ɱɚɫɬɨɬɵ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɝɨ ɬɢɩɚ

Ⱦɥɹ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɣ ɫɯɟɦɵ ɚɧɚɥɢɡ ɩɪɨɜɨɞɢɬɫɹ ɚɧɚɥɨɝɢɱɧɨ, ɫ ɬɨɣ ɪɚɡɧɢ-

ɰɟɣ, ɱɬɨ ɧɚ ɩɟɪɟɯɨɞɟ ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɢɦɟɟɦ ɫɭɦɦɭ ɩɨɫɬɨɹɧɧɨɝɨ ɢ ɞɜɭɯ ɝɚɪɦɨ-

ɧɢɱɟɫɤɢɯ ɧɚɩɪɹɠɟɧɢɣ:

u = U

0

+ U

1

sin

ω

1

t + U

n

sin(N

ω

1

t+

ϕ

N

),

ɚ ɬɨɤ ɱɟɪɟɡ ɞɢɨɞ

i = Cdu/dt

ɹɜɥɹɟɬɫɹ ɧɟɥɢɧɟɣɧɨɣ ɮɭɧɤɰɢɟɣ ɧɚɩɪɹɠɟɧɢɹ.

Ɇɵ ɡɞɟɫɶ ɧɟ ɛɭɞɟɦ ɩɪɨɜɨɞɢɬɶ ɩɨɞɪɨɛɧɵɣ ɚɧɚɥɢɡ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɣ ɫɯɟɦɵ,

ɚ ɨɝɪɚɧɢɱɢɦɫɹ ɫɚɦɵɦɢ ɨɛɳɢɦɢ ɡɚɦɟɱɚɧɢɹɦɢ. ɗɤɜɢɜɚɥɟɧɬɧɚɹ ɫɯɟɦɚ ɜɚɪɚɤɬɨɪɚ ɜ

ɫɨɫɬɚɜɟ ɭɦɧɨɠɢɬɟɥɹ ɱɚɫɬɨɬɵ ɜ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɣ ɫɯɟɦɟ ɢɦɟɟɬ ɜɢɞ, ɩɨɤɚɡɚɧɧɵɣ

ɧɚ ɪɢɫ. 4.8.

Z

ɜɯ

R

1s

R

1ɷ

C

1ɷ

i

N

C

Nɷ

R

Ns

R

ɧ

Ɋɢɫ. 4.8. ɗɤɜɢɜɚɥɟɧɬɧɚɹ ɫɯɟɦɚ ɜɚɪɚɤɬɨɪɚ ɜ ɭɦɧɨɠɢɬɟɥɟ ɱɚɫɬɨɬɵ

ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɝɨ ɬɢɩɚ

ɇɚ ɪɢɫ. 4.8

R

1ɷ

— ɷɤɜɢɜɚɥɟɧɬɧɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɞɢɨɞɚ ɩɨ ɩɟɪɜɨɣ ɝɚɪɦɨ-

ɧɢɤɟ;

C

1ɷ

ɢ

C

Nɷ

— ɷɤɜɢɜɚɥɟɧɬɧɵɟ ɺɦɤɨɫɬɢ ɩɨ ɩɟɪɜɨɣ ɢ N-ɣ ɝɚɪɦɨɧɢɤɚɦ;

R

C R

R

N C R

s

sN

s

1

2

0

2 2

1

2

0

2

1 1

= =

ω ω

ɢ

— ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɩɨɬɟɪɶ p-n ɩɟɪɟɯɨɞɚ ɧɚ ɜɯɨɞɧɨɣ ɢ ɜɵɯɨɞɧɨɣ ɱɚɫɬɨɬɚɯ,

ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ, ɩɟɪɟɫɱɢɬɚɧɧɵɟ ɜ ɩɚɪɚɥɥɟɥɶɧɭɸ ɫɯɟɦɭ.

Ʉɨɷɮɮɢɰɢɟɧɬ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɢɦɟɟɬ ɜɢɞ

η

=

+

⋅

+

R

R R

R

R R

ɷ

s ɷ

ɧ

sN ɧ

1

1 1

.

4.7. ɋɪɚɜɧɢɬɟɥɶɧɚɹ ɨɰɟɧɤɚ ɫɯɟɦ ɢ ɪɟɠɢɦɨɜ

ɪɚɛɨɬɵ ɭɦɧɨɠɢɬɟɥɹ ɱɚɫɬɨɬɵ

ɉɚɪɚɥɥɟɥɶɧɚɹ ɫɯɟɦɚ ɨɛɥɚɞɚɟɬ ɫɥɟɞɭɸɳɢɦɢ ɩɪɟɢɦɭɳɟɫɬɜɚɦɢ ɩɟɪɟɞ ɩɨɫɥɟ-

ɞɨɜɚɬɟɥɶɧɨɣ:

ɚ) ɩɪɨɫɬɚɹ ɜɨɡɦɨɠɧɨɫɬɶ ɤɨɦɩɟɧɫɚɰɢɢ ɢɧɞɭɤɬɢɜɧɨɫɬɢ ɜɵɜɨɞɨɜ;

ɛ) ɯɨɪɨɲɢɣ ɬɟɩɥɨɨɬɜɨɞ, ɱɬɨ ɩɨɡɜɨɥɹɟɬ ɩɨɥɭɱɚɬɶ ɛɨɥɟɟ ɜɵɫɨɤɭɸ ɦɨɳɧɨɫɬɶ;

49

ɜ) ɛɨ′ɥɶɲɢɣ ɄɉȾ, ɬɚɤ ɤɚɤ ɱɟɪɟɡ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɩɨɬɟɪɶ

R

s

ɩɪɨɬɟɤɚɸɬ ɬɨɥɶɤɨ

ɞɜɟ ɝɚɪɦɨɧɢɱɟɫɤɢɟ ɫɨɫɬɚɜɥɹɸɳɢɟ ɬɨɤɚ.

ɇɟɞɨɫɬɚɬɤɢ ɩɚɪɚɥɥɟɥɶɧɨɣ ɫɯɟɦɵ ɫɜɨɞɹɬɫɹ ɤ ɫɥɟɞɭɸɳɟɦɭ:

ɚ) ɦɚɥɨɟ ɜɯɨɞɧɨɟ ɢ ɜɵɯɨɞɧɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ (ɟɞɢɧɢɰɵ Ɉɦ) ɫɨɡɞɚɸɬ

ɬɪɭɞɧɨɫɬɢ ɢɯ ɫɨɝɥɚɫɨɜɚɧɢɹ;

ɛ) ɜ ɪɟɠɢɦɟ ɩɨɥɧɨɝɨ ɡɚɩɢɪɚɧɢɹ ɜɨɡɦɨɠɟɧ ɦɟɧɶɲɢɣ ɤɨɷɮɮɢɰɢɟɧɬ ɭɦɧɨ-

ɠɟɧɢɹ, ɧɚɩɪɢɦɟɪ, ɞɥɹ ɞɢɨɞɨɜ ɫ ɪɟɡɤɢɦ ɩɟɪɟɯɨɞɨɦ ɜɨɡɦɨɠɧɨ ɬɨɥɶɤɨ ɭɞɜɨɟɧɢɟ

ɱɚɫɬɨɬɵ.

Ⱦɨɫɬɨɢɧɫɬɜɚ ɢ ɧɟɞɨɫɬɚɬɤɢ ɩɚɪɚɥɥɟɥɶɧɨɣ ɫɯɟɦɵ ɫɮɨɪɦɭɥɢɪɨɜɚɧɵ ɨɬɧɨ-

ɫɢɬɟɥɶɧɨ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɣ, ɩɨɷɬɨɦɭ ɧɟɞɨɫɬɚɬɤɢ ɨɞɧɨɣ ɫɯɟɦɵ ɹɜɥɹɸɬɫɹ ɨɬɧɨ-

ɫɢɬɟɥɶɧɵɦɢ ɞɨɫɬɨɢɧɫɬɜɚɦɢ ɞɪɭɝɨɣ.

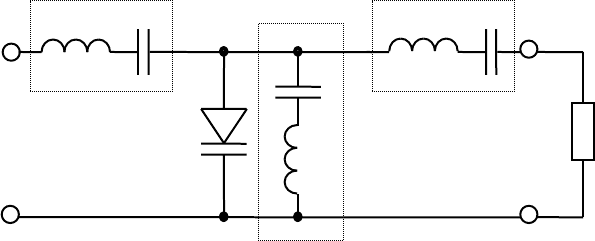
ȼ ɪɹɞɟ ɫɥɭɱɚɟɜ ɦɨɠɧɨ ɭɜɟɥɢɱɢɬɶ ɤɨɷɮɮɢɰɢɟɧɬ ɭɦɧɨɠɟɧɢɹ ɩɚɪɚɥɥɟɥɶɧɨɣ

ɫɯɟɦɵ ɫ ɩɨɦɨɳɶɸ ɯɨɥɨɫɬɵɯ ɤɨɧɬɭɪɨɜ (ɪɢɫ. 4.9). ɏɨɥɨɫɬɨɣ ɤɨɧɬɭɪ — ɷɬɨ ɤɨɧɬɭɪ

(ɱɢɬɚɣ — ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɵɣ ɪɟɡɨɧɚɧɫɧɵɣ ɤɨɧɬɭɪ), ɩɨɞɫɨɟɞɢɧɟɧɧɵɣ

ɩɚɪɚɥɥɟɥɶɧɨ ɤ ɞɢɨɞɭ ɢ ɧɚɫɬɪɨɟɧɧɵɣ ɧɚ ɩɪɨɦɟɠɭɬɨɱɧɭɸ ɱɚɫɬɨɬɭ. ɗɬɨɬ ɤɨɧɬɭɪ

ɧɟ ɫɜɹɡɚɧ ɫ ɧɚɝɪɭɡɤɨɣ ɢ ɧɟ ɩɟɪɟɞɚɟɬ ɧɢ ɤɭɞɚ ɷɧɟɪɝɢɸ. ȿɝɨ ɡɚɞɚɱɚ ɨɛɟɫɩɟɱɢɬɶ

ɩɪɨɬɟɤɚɧɢɟ ɱɟɪɟɡ ɞɢɨɞ ɩɪɨɦɟɠɭɬɨɱɧɨɣ ɝɚɪɦɨɧɢɤɢ ɬɨɤɚ ɞɥɹ ɬɨɝɨ, ɱɬɨɛɵ ɨɧɚ

ɩɪɟɨɛɪɚɡɨɜɚɥɚɫɶ ɜ ɛɨɥɟɟ ɜɵɫɨɤɨɱɚɫɬɨɬɧɵɟ ɤɨɥɟɛɚɧɢɹ. ȼɨɡɦɨɠɧɨ ɩɪɢɦɟɧɟɧɢɟ

ɧɟɫɤɨɥɶɤɢɯ ɯɨɥɨɫɬɵɯ ɤɨɧɬɭɪɨɜ. Ɉɫɧɨɜɧɨɣ ɧɟɞɨɫɬɚɬɨɤ ɬɚɤɢɯ ɫɯɟɦ — ɛɨɥɟɟ ɭɡɤɚɹ

ɩɨɥɨɫɚ ɱɚɫɬɨɬ (ɦɟɧɟɟ 1%, ɬɨɝɞɚ ɤɚɤ ɭ ɞɜɭɯɤɨɧɬɭɪɧɵɯ — ɧɟɫɤɨɥɶɤɨ ɩɪɨɰɟɧɬɨɜ).

Ɏ

1

Ɏ

N

Ɏ

k

ɯɨɥɨɫɬɨɣ

R

ɧ

ɤɨɧɬɭɪ (0<

k

<N)

Ɋɢɫ. 4.9. ɍɦɧɨɠɢɬɟɥɶ ɱɚɫɬɨɬɵ ɫ ɯɨɥɨɫɬɵɦ ɤɨɧɬɭɪɨɦ

ɋɪɚɜɧɢɦ ɬɟɩɟɪɶ ɜɨɡɦɨɠɧɨɫɬɢ ɪɚɡɥɢɱɧɵɯ ɪɟɠɢɦɨɜ ɪɚɛɨɬɵ ɞɢɨɞɚ: ɫ ɩɨɥɧɵɦ

ɡɚɩɢɪɚɧɢɟɦ ɩɟɪɟɯɨɞɚ ɢ ɫ ɱɚɫɬɢɱɧɵɦ ɨɬɩɢɪɚɧɢɟɦ.

ɉɪɢ ɦɚɥɵɯ ɤɨɷɮɮɢɰɢɟɧɬɚɯ ɭɦɧɨɠɟɧɢɹ N = 2, 3 ɷɧɟɪɝɟɬɢɱɟɫɤɢɟ ɩɚɪɚɦɟɬɪɵ

ɨɛɨɢɯ ɪɟɠɢɦɨɜ ɩɪɢɦɟɪɧɨ ɨɞɢɧɚɤɨɜɵ. ɉɪɢ N = 4..6 ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɟɨɛɪɚ-

ɡɨɜɚɧɢɹ ɪɟɠɢɦɚ ɫ ɱɚɫɬɢɱɧɵɦ ɨɬɩɢɪɚɧɢɟɦ ɡɧɚɱɢɬɟɥɶɧɨ ɜɵɲɟ. Ʉɪɨɦɟ ɬɨɝɨ, ɜ

ɷɬɨɦ ɪɟɠɢɦɟ ɜɨɡɦɨɠɧɨ ɩɨɥɭɱɚɬɶ ɛɨ′ɥɶɲɭɸ ɜɵɯɨɞɧɭɸ ɦɨɳɧɨɫɬɶ, ɬɚɤ ɤɚɤ ɡɞɟɫɶ

ɞɨɩɭɫɬɢɦɚ ɛɨ′ɥɶɲɚɹ ɚɦɩɥɢɬɭɞɚ ɤɨɥɟɛɚɧɢɣ ɧɚɩɪɹɠɟɧɢɹ ɢɡ-ɡɚ ɜɨɡɦɨɠɧɨɫɬɢ

ɡɚɯɨɞɚ ɜ ɨɛɥɚɫɬɶ ɨɬɩɢɪɚɧɢɹ ɞɢɨɞɚ.

Ɉɫɧɨɜɧɨɣ ɧɟɞɨɫɬɚɬɨɤ ɪɟɠɢɦɚ ɫ ɱɚɫɬɢɱɧɵɦ ɨɬɩɢɪɚɧɢɟɦ ɞɢɨɞɚ — ɨɝɪɚ-

ɧɢɱɟɧɧɵɣ ɱɚɫɬɨɬɧɵɣ ɞɢɚɩɚɡɨɧ. ɇɚ ɱɚɫɬɨɬɚɯ ɛɨɥɟɟ 10 ȽȽɰ ɜɨɡɦɨɠɧɨ ɢɫɩɨɥɶ-

ɡɨɜɚɧɢɟ ɬɨɥɶɤɨ ɪɟɠɢɦɚ ɡɚɩɟɪɬɨɝɨ ɞɢɨɞɚ.

50

Ƚɥɚɜɚ 5. ȺȼɌɈȽȿɇȿɊȺɌɈɊɕ

5.1. Ɉɛɳɢɟ ɫɜɟɞɟɧɢɹ. ɍɪɚɜɧɟɧɢɟ ɚɜɬɨɝɟɧɟɪɚɬɨɪɚ

Ⱥɜɬɨɝɟɧɟɪɚɬɨɪɚɦɢ (ȺȽ) ɹɜɥɹɸɬɫɹ ɭɫɬɪɨɣɫɬɜɚ, ɜ ɤɨɬɨɪɵɯ ɷɧɟɪɝɢɹ ɢɫɬɨɱɧɢɤɚ

ɩɢɬɚɧɢɹ ɩɪɟɨɛɪɚɡɭɟɬɫɹ ɜ ɷɧɟɪɝɢɸ ɜɵɫɨɤɨɱɚɫɬɨɬɧɵɯ ɤɨɥɟɛɚɧɢɣ ɛɟɡ ɜɧɟɲɧɟɝɨ

ɜɨɡɛɭɠɞɟɧɢɹ.

ȺȽ ɹɜɥɹɸɬɫɹ ɩɟɪɜɢɱɧɵɦɢ ɢɫɬɨɱɧɢɤɚɦɢ ɤɨɥɟɛɚɧɢɣ, ɱɚɫɬɨɬɚ ɢ ɚɦɩɥɢɬɭɞɚ

ɤɨɬɨɪɵɯ ɨɩɪɟɞɟɥɹɸɬɫɹ ɬɨɥɶɤɨ ɫɨɛɫɬɜɟɧɧɵɦɢ ɩɚɪɚɦɟɬɪɚɦɢ ɫɯɟɦɵ ɢ ɞɨɥɠɧɵ ɜ

ɨɱɟɧɶ ɦɚɥɨɣ ɫɬɟɩɟɧɢ ɡɚɜɢɫɟɬɶ ɨɬ ɜɧɟɲɧɢɯ ɭɫɥɨɜɢɣ.

ȼ ɥɸɛɨɦ ȺȽ ɦɨɠɧɨ ɜɵɞɟɥɢɬɶ ɤɨɥɟɛɚɬɟɥɶɧɭɸ ɫɢɫɬɟɦɭ (Ʉɋ), ɤɨɥɟɛɚɧɢɹ ɜ

ɤɨɬɨɪɨɣ ɩɨɞɞɟɪɠɢɜɚɸɬɫɹ ɡɚ ɫɱɟɬ ɩɨɫɬɭɩɥɟɧɢɹ ɩɨɪɰɢɣ ɷɧɟɪɝɢɢ ɨɬ ɢɫɬɨɱɧɢɤɚ

ɩɢɬɚɧɢɹ. ɍɩɪɚɜɥɹɟɬ ɷɬɢɦ ɩɪɨɰɟɫɫɨɦ ɚɤɬɢɜɧɵɣ ɷɥɟɦɟɧɬ (Ⱥɗ) ɜ ɜɢɞɟ ɞɜɭɯ-

ɩɨɥɸɫɧɢɤɚ (ɬɭɧɧɟɥɶɧɵɣ ɞɢɨɞ, ɞɢɨɞ Ƚɚɧɧɚ ɢ ɞɪ.) ɢɥɢ ɬɪɟɯɩɨɥɸɫɧɢɤɚ

(ɬɪɚɧɡɢɫɬɨɪ, ɥɚɦɩɚ), ɢ ɧɚ ɤɨɬɨɪɵɣ ɜɨɡɞɟɣɫɬɜɭɸɬ ɤɨɥɟɛɚɧɢɹ, ɩɨɫɬɭɩɚɸɳɢɟ ɢɡ

Ʉɋ.

ɉɪɟɞɦɟɬɨɦ ɪɚɫɫɦɨɬɪɟɧɢɹ ɞɚɧɧɨɣ ɝɥɚɜɵ ɛɭɞɭɬ ɬɪɚɧɡɢɫɬɨɪɧɵɟ ȺȽ, ɨɛɨɛ-

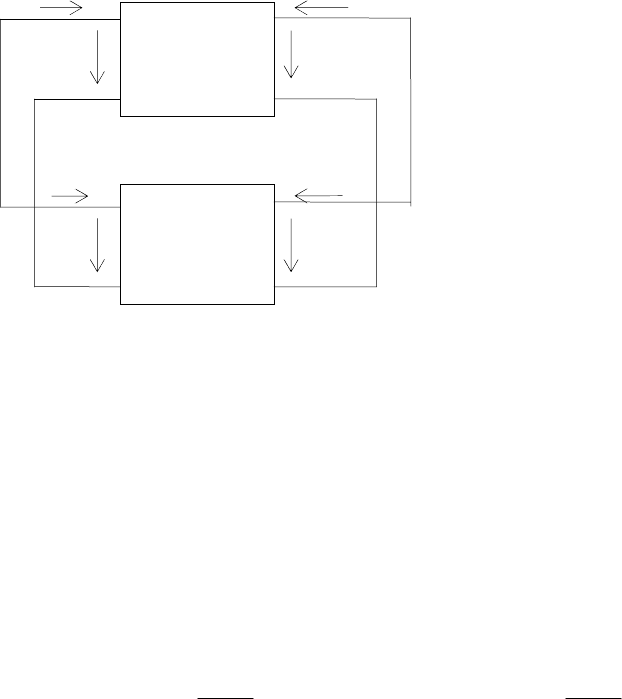
ɳɟɧɧɭɸ ɫɯɟɦɭ ɤɨɬɨɪɵɯ ɦɨɠɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɜ ɜɢɞɟ, ɩɨɤɚɡɚɧɧɨɦ ɧɚ ɪɢɫ.5.1. ɇɚ

ɫɯɟɦɟ ɨɛɨɡɧɚɱɟɧɢɹ ɬɨɤɨɜ ɢ ɧɚɩɪɹɠɟ-

ɧɢɣ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɨɛɳɟɦɭ ɫɥɭɱɚɸ.

Ɇɵ ɩɪɢ ɚɧɚɥɢɡɟ ȺȽ ɚɤɬɢɜɧɵɣ ɱɟɬɵ-

ɪɟɯɩɨɥɸɫɧɢɤ ɛɭɞɟɦ ɫɱɢɬɚɬɶ ɢɞɟɚɥɶ-

ɧɵɦ, ɬ.ɟ. ɬɚɤɢɦ, ɭ ɤɨɬɨɪɨɝɨ ɜɯɨɞɧɨɟ

ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɛɟɫɤɨɧɟɱɧɨ ɜɟɥɢɤɨ

(

I

ɜɯ

= 0), ɢ ɨɬɫɭɬɫɬɜɭɟɬ ɜɥɢɹɧɢɟ ɜɵ-

ɯɨɞɧɨɝɨ ɧɚɩɪɹɠɟɧɢɹ

U

ɜɵɯ

ɧɚ ɜɵɯɨɞ-

ɧɨɣ ɬɨɤ

I

ɜɵɯ

. Ⱦɥɹ ɛɨɥɶɲɢɧɫɬɜɚ ɩɪɚɤ-

ɬɢɱɟɫɤɢɯ ɫɥɭɱɚɟɜ ɬɚɤɨɟ ɩɪɟɞɩɨ-

ɥɨɠɟɧɢɟ ɦɨɠɧɨ ɞɨɩɭɫɬɢɬɶ ɢɥɢ

ɩɪɟɨɛɪɚɡɨɜɚɬɶ ɪɟɚɥɶɧɵɣ ɱɟɬɵɪɟɯɩɨ-

ɥɸɫɧɢɤ ɤ ɢɞɟɚɥɶɧɨɦɭ. ȼɵɯɨɞɧɨɣ ɬɨɤ

I

ɜɵɯ

ɢɞɟɚɥɶɧɨɝɨ ɱɟɬɵɪɟɯɩɨɥɸɫɧɢɤɚ

ɡɚɜɢɫɢɬ ɨɬ ɩɪɢɥɨɠɟɧɧɨɝɨ ɧɚ ɜɯɨɞ ɧɚɩɪɹɠɟɧɢɹ:

I

ɜɵɯ

= U

ɜɯ

S

1

; S

1

= S

1

exp(j

ϕ

s

),

ɝɞɟ

S

1

=

S

1

(

U

ɜɯ

) — ɭɫɪɟɞɧɟɧɧɚɹ ɩɨ ɩɟɪɜɨɣ ɝɚɪɦɨɧɢɤɟ ɤɪɭɬɢɡɧɚ ɩɪɨɯɨɞɧɨɣ

ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ, ɤɨɬɨɪɚɹ ɡɚɜɢɫɢɬ ɨɬ ɚɦɩɥɢɬɭɞɵ ɜɯɨɞɧɨɝɨ ɧɚɩɪɹɠɟɧɢɹ;

ϕ

s

— ɮɚɡɨɜɚɹ ɡɚɞɟɪɠɤɚ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ

I

ɜɵɯ

ɨɬ ɭɩɪɚɜɥɹɸɳɟɝɨ ɜɯɨɞɧɨɝɨ

ɧɚɩɪɹɠɟɧɢɹ

U

ɜɯ

.

ȼɜɟɞɟɦ ɤɨɷɮɮɢɰɢɟɧɬ ɨɛɪɚɬɧɨɣ ɫɜɹɡɢ

k

ɨɫ

ɢ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɧɚɝɪɭɡɤɢ

Z

ɧ

:

k

U

Z

U

I

ɨɫ

ɜɯ

ɜɵɯ

k ɧ

ɜɵɯ

ɧ ɧ

k j Z j= − = ⋅ = = ⋅exp( ); exp( ).

ϕ ϕ

ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɭɪɚɜɧɟɧɢɟ ɚɜɬɨɝɟɧɟɪɚɬɨɪɚ ɢɦɟɟɬ ɜɢɞ

S

1

k

ɨɫ

Z

ɧ

= 1

. (5.2)

I

ɜɯ

I

ɜɵɯ

Ⱥɤɬɢɜɧɵɣ

U

ɜɯ

ɱɟɬɵɪɟɯ-

U

ɜɵɯ

ɩɨɥɸɫɧɢɤ

–I

ɜɯ

–I

ɜɵɯ

ɉɚɫɫɢɜɧɵɣ

U

ɜɯ

ɱɟɬɵɪɟɯ-

U

ɜɵɯ

ɩɨɥɸɫɧɢɤ

Ɋɢɫ. 5.1. Ɉɛɨɛɳɟɧɧɚɹ ɫɯɟɦɚ ȺȽ

(5.1)

Воробьев М.С. Устройства генерирования радиосигналов

Подождите немного. Документ загружается.