Воробьев М.С. Устройства генерирования радиосигналов

i

ɜɵɯ

i

ɜɵɯ

i

ɜɵɯ

i

′′

ɜɵɯ

S

ɤɪ

U

ɧ

i

′

ɜɵɯ

i

″

ɜɵɯ

S

ɤɪ

ȿ

ɉ

S(E

ɫɦ

–E

′

+U

ɜɯ

) i

′

ɜɵɯ

U

ɜɯ

= U

ɜɯ max

E

ɫɦ

E

′

u

ɜɯ

τ

E

ɉ

u

ɜɵɯ

θ

ɚ) ɛ) ɜ) U

ɧ

2

θ

u

ɜɯ

ɇɊ ɄɊ ɉɊ u

ɜɵɯ

U

ɜɯ

|E

′

– E

ɫɦ

|

τ

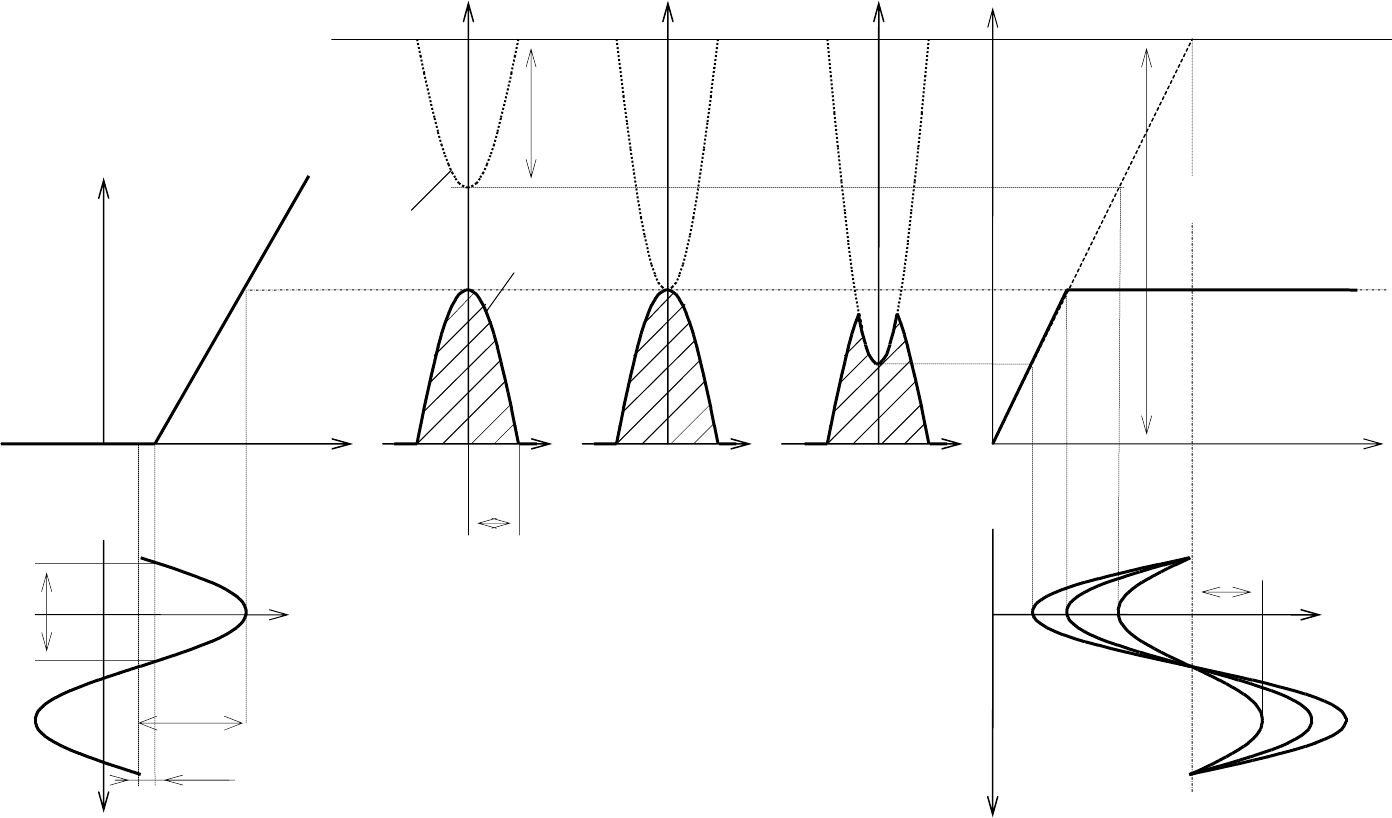
Ɋɢɫ. 1.6. ɂɦɩɭɥɶɫɵ ɬɨɤɚ ɜ ɛɟɡɵɧɟɪɰɢɨɧɧɨɦ Ⱥɗ

12

ɇɚɩɪɢɦɟɪ, ɞɥɹ ɥɚɦɩɵ ɷɬɨ ɦɨɠɟɬ ɨɡɧɚɱɚɬɶ ɩɟɪɟɝɪɟɜ ɫɟɬɤɢ, ɚ ɞɥɹ ɬɪɚɧɡɢɫɬɨɪɚ

— ɩɟɪɟɝɪɟɜ ɛɚɡɨɜɨɣ ɨɛɥɚɫɬɢ.

ȿɫɥɢ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɧɚɝɪɭɡɤɢ ɢɦɟɟɬ ɪɟɚɤɬɢɜɧɭɸ ɫɨɫɬɚɜɥɹɸɳɭɸ ɧɚ

ɱɚɫɬɨɬɟ 1-ɣ ɝɚɪɦɨɧɢɤɢ, ɬɨ ɦɢɧɢɦɭɦ ɧɚɩɪɹɠɟɧɢɹ

E

ɉ

– u

ɧ

(

τ

)

ɫɞɜɢɧɭɬ ɨɬɧɨɫɢ-

ɬɟɥɶɧɨ ɦɚɤɫɢɦɭɦɚ

u

ɜɯ

(

τ

)

. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɢ ɩɪɨɜɚɥ ɜ ɜɵɯɨɞɧɨɦ ɢɦɩɭɥɶɫɟ ɬɨɤɚ

ɛɭɞɟɬ ɫɦɟɳɟɧ.

1.4. ɇɚɝɪɭɡɨɱɧɵɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ Ƚȼȼ

Ɂɚɜɢɫɢɦɨɫɬɢ ɬɨɤɨɜ, ɧɚɩɪɹɠɟɧɢɣ ɢ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɩɚɪɚɦɟɬɪɨɜ Ⱥɗ ɨɬ

ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɧɚɝɪɭɡɤɢ ɩɪɢ ɧɟɢɡɦɟɧɧɵɯ ɧɚɩɪɹɠɟɧɢɹɯ

u

ɜɯ

,

E

ɉ

,

E

ɫɦ

ɧɚɡɵɜɚɸɬɫɹ

ɧɚɝɪɭɡɨɱɧɵɦɢ ɯɚɪɚɤɬɟɪɢɫɬɢɤɚɦɢ. Ȼɭɞɟɦ

ɫɱɢɬɚɬɶ, ɱɬɨ ɧɚɝɪɭɡɤɚ ɹɜɥɹɟɬɫɹ ɚɤɬɢɜɧɨɣ:

Z

ɧ

= R

ɧ

. ɂɡɦɟɧɟɧɢɟ

R

ɧ

ɜɥɟɱɟɬ ɢɡɦɟɧɟɧɢɟ

ɧɚɩɪɹɠɟɧɢɹ

U

ɧ

= I

ɜɵɯ1

R

ɧ

. Ɋɚɫɫɦɨɬɪɢɦ ɤɚɤ

ɩɪɢ ɷɬɨɦ ɢɡɦɟɧɹɟɬɫɹ ɪɟɠɢɦ ɪɚɛɨɬɵ Ⱥɗ.

ɉɪɢ ɦɚɥɵɯ ɡɧɚɱɟɧɢɹɯ

R

ɧ

ɦɚɥɨ

U

ɧ

, ɢ Ⱥɗ ɧɚ-

ɯɨɞɢɬɫɹ ɜ ɇɊ. ȼ ɷɬɨɦ ɪɟɠɢɦɟ ɫ ɪɨɫɬɨɦ

R

ɧ

ɩɪɨɢɫɯɨɞɢɬ ɫɥɟɞɭɸɳɟɟ:

• ɮɨɪɦɚ ɢɦɩɭɥɶɫɚ ɬɨɤɚ ɧɟ ɢɡɦɟɧɹɟɬɫɹ,

ɫɥɟɞɨɜɚɬɟɥɶɧɨ,

g

1

= const

;

• ɩɨɫɬɨɹɧɧɵɦɢ ɞɨɥɠɧɵ ɨɫɬɚɜɚɬɶɫɹ ɢ

ɚɦɩɥɢɬɭɞɵ ɬɨɤɨɜ

I

ɜɵɯ0

, I

ɜɵɯ1

, ɧɨ ɜ ɪɟɚɥɶ-

ɧɵɯ Ⱥɗ ɭɜɟɥɢɱɟɧɢɟ

U

ɧ

ɜɫɟɝɞɚ ɩɪɢɜɨɞɢɬ

ɤ ɭɦɟɧɶɲɟɧɢɸ ɚɦɩɥɢɬɭɞɵ ɢɦɩɭɥɶɫɚ ɢ,

ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɤ ɧɟɡɧɚɱɢɬɟɥɶɧɨɦɭ

ɭɦɟɧɶɲɟɧɢɸ

I

ɜɵɯ0

,

I

ɜɵɯ1

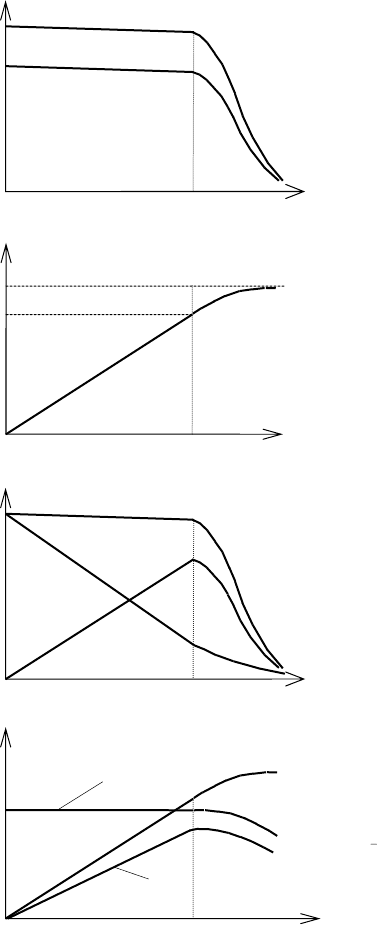
, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ

ɪɢɫ. 1.7, ɚ;

• ɧɚɩɪɹɠɟɧɢɟ

U

ɧ

ɢ ɤɨɷɮɮɢɰɢɟɧɬ

ξ

ɥɢɧɟɣɧɨ ɧɚɪɚɫɬɚɸɬ (ɪɢɫ. 1.7, ɛ ɢ ɝ);

• ɩɨɬɪɟɛɥɹɟɦɚɹ ɨɬ ɢɫɬɨɱɧɢɤɚ ɦɨɳɧɨɫɬɶ

P

0

ɧɟɡɧɚɱɢɬɟɥɶɧɨ ɫɧɢɠɚɟɬɫɹ ɢɡ-ɡɚ ɫɧɢɠɟɧɢɹ

I

ɜɵɯ0

;

• ɜɵɯɨɞɧɚɹ ɦɨɳɧɨɫɬɶ

P

1

ɥɢɧɟɣɧɨ ɧɚɪɚɫ-

ɬɚɟɬ, ɚ ɦɨɳɧɨɫɬɶ ɪɚɫɫɟɹɧɢɹ

P

ɪɚɫɫ

ɩɚɞɚɟɬ.

ɉɪɢ

R

ɧ

=

R

ɧ ɤɪ

ɢɦɟɟɬ ɦɟɫɬɨ ɤɪɢɬɢ-

ɱɟɫɤɢɣ ɪɟɠɢɦ, ɚ ɩɪɢ ɞɚɥɶɧɟɣɲɟɦ

ɭɜɟɥɢɱɟɧɢɢ

R

ɧ

Ⱥɗ ɩɟɪɟɯɨɞɢɬ ɜ ɉɊ. ȼ

ɩɟɪɟɧɚɩɪɹɠɟɧɧɨɦ ɪɟɠɢɦɟ ɨɫɧɨɜɧɵɟ ɩɚɪɚ-

ɦɟɬɪɵ ɜɟɞɭɬ ɫɟɛɹ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:

• ɢɡ-ɡɚ ɩɨɹɜɢɜɲɟɝɨɫɹ ɩɪɨɜɚɥɚ ɜ ɢɦɩɭɥɶɫɟ

ɩɪɨɢɫɯɨɞɢɬ ɛɵɫɬɪɨɟ ɭɦɟɧɶɲɟɧɢɟ ɬɨɤɨɜ

I

ɜɵɯ0

,

I

ɜɵɯ1

, ɩɪɢɱɟɦ, ɩɨɫɬɨɹɧɧɚɹ

I

ɜɵɯ1

, I

ɜɵɯ1

I

ɜɵɯ0

ɉɊ

I

ɜɵɯ0

ɇɊ

ɚ)

R

ɧ ɤɪ

R

ɧ

U

ɧ

E

ɉ

U

ɧ ɤɪ

ɛ)

R

ɧ ɤɪ

R

ɧ

P

0

,P

1

, P

0

P

ɪɚɫɫ

P

ɪɚɫɫ

P

1

ɜ)

R

ɧ ɤɪ

R

ɧ

ξ

,g

1

η

ɷ

g

1

/2

ξ

η

ɷ

ɝ)

R

ɧ ɤɪ

R

ɧ

Ɋɢɫ. 1.7. ɇɚɝɪɭɡɨɱɧɵɟ ɯɚɪɚɤ-

ɬɟɪɢɫ

ɬɢɤɢ Ƚȼȼ

13

ɫɨɫɬɚɜɥɹɸɳɚɹ ɭɦɟɧɶɲɚɟɬɫɹ ɦɟɞɥɟɧɧɟɟ, ɩɨɷɬɨɦɭ ɫɧɢɠɚɟɬɫɹ ɜɟɥɢɱɢɧɚ

ɤɨɷɮɮɢɰɢɟɧɬɚ ɮɨɪɦɵ ɬɨɤɚ

g

1

(ɪɢɫ. 1.7, ɚ, ɝ);

• ɫɤɨɪɨɫɬɶ ɪɨɫɬɚ ɧɚɩɪɹɠɟɧɢɹ

U

ɧ

ɢ ɤɨɷɮɮɢɰɢɟɧɬɚ

ξ

ɫɧɢɠɚɟɬɫɹ ɬɚɤ, ɱɬɨ ɜ

ɩɟɪɜɨɦ ɩɪɢɛɥɢɠɟɧɢɢ ɢɯ ɦɨɠɧɨ ɫɱɢɬɚɬɶ ɩɨɫɬɨɹɧɧɵɦɢ ɜɟɥɢɱɢɧɚɦɢ;

• ɦɨɳɧɨɫɬɶ ɩɨɬɪɟɛɥɟɧɢɹ

P

0

ɢ ɜɵɯɨɞɧɚɹ ɦɨɳɧɨɫɬɶ

P

1

ɩɚɞɚɸɬ ɩɪɨɩɨɪ-

ɰɢɨɧɚɥɶɧɨ

I

ɜɵɯ0

ɢ

I

ɜɵɯ1

, ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ (ɪɢɫ. 1.7, ɜ).

ɉɪɨɚɧɚɥɢɡɢɪɭɟɦ ɩɨɥɭɱɟɧɧɵɟ ɪɟɡɭɥɶɬɚɬɵ. ɗɥɟɤɬɪɨɧɧɵɣ ɄɉȾ, ɨɩɪɟ-

ɞɟɥɹɟɦɵɣ ɩɨ (1.5), ɢɦɟɟɬ ɬɭɩɨɣ ɦɚɤɫɢɦɭɦ ɜ ɉɊ (ɪɢɫ.1.7, ɝ). Ɇɚɤɫɢɦɚɥɶɧɚɹ

ɜɵɯɨɞɧɚɹ ɦɨɳɧɨɫɬɶ ɧɚɛɥɸɞɚɟɬɫɹ ɜ ɄɊ. ɉɪɚɤɬɢɤɚ ɩɨɤɚɡɵɜɚɟɬ, ɱɬɨ ɦɚɤɫɢ-

ɦɚɥɶɧɵɣ ɤɨɷɮɮɢɰɢɟɧɬ ɭɫɢɥɟɧɢɹ ɬɚɤɠɟ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɄɊ. ȼ ɫɜɹɡɢ ɫ ɷɬɢɦ, ɤɪɢ-

ɬɢɱɟɫɤɢɣ ɪɟɠɢɦ ɹɜɥɹɟɬɫɹ ɨɩɬɢɦɚɥɶɧɵɦ, ɢ ɫɱɢɬɚɟɬɫɹ ɨɫɧɨɜɧɵɦ. Ⱦɜɚ ɞɪɭɝɢɯ

ɪɟɠɢɦɚ ɬɚɤɠɟ ɩɪɢɦɟɧɹɸɬɫɹ ɜ ɫɩɟɰɢɚɥɶɧɵɯ ɤɚɫɤɚɞɚɯ, ɨ ɤɨɬɨɪɵɯ ɩɨɣɞɟɬ ɪɟɱɶ

ɧɢɠɟ. ɋɟɣɱɚɫ ɜɚɠɧɨ ɨɬɦɟɬɢɬɶ, ɱɬɨ ɄɉȾ ɉɊ ɫɭɳɟɫɬɜɟɧɧɨ ɜɵɲɟ ɄɉȾ ɝɥɭɛɨɤɨɝɨ

ɇɊ. ȼ ɩɨɫɥɟɞɧɟɦ ɫɥɭɱɚɟ ɜɨɡɦɨɠɟɧ ɩɟɪɟɝɪɟɜ Ⱥɗ ɢɡ-ɡɚ ɡɧɚɱɢɬɟɥɶɧɨɣ ɦɨɳɧɨɫɬɢ

ɪɚɫɫɟɹɧɢɹ.

1.5. ȼɥɢɹɧɢɟ ɩɢɬɚɸɳɢɯ ɧɚɩɪɹɠɟɧɢɣ ɢ ɚɦɩɥɢɬɭɞɵ

ɜɨɡɛɭɠɞɟɧɢɹ ɧɚ ɪɟɠɢɦ ɪɚɛɨɬɵ ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ

ȼɟɥɢɱɢɧɵ ɧɚɩɪɹɠɟɧɢɣ ɩɢɬɚɧɢɹ

E

ɉ

ɢ ɫɦɟɳɟɧɢɹ

E

ɫɦ

ɢ ɚɦɩɥɢɬɭɞɵ

ɜɨɡɛɭɠɞɟɧɢɹ

U

ɜɯ

ɹɜɥɹɸɬɫɹ ɜɚɠɧɵɦɢ ɩɚɪɚɦɟɬɪɚɦɢ, ɩɨɡɜɨɥɹɸɳɢɦɢ ɪɟɝɭ-

ɥɢɪɨɜɚɬɶ ɪɟɠɢɦ ɪɚɛɨɬɵ Ƚȼȼ. ɉɪɨɚɧɚɥɢɡɢɪɭɟɦ ɜɥɢɹɧɢɟ ɷɬɢɯ ɩɚɪɚɦɟɬɪɨɜ ɧɚ

ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ Ƚȼȼ ɧɚ ɩɪɢɦɟɪɟ ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ.

Ɋɚɫɫɦɨɬɪɢɦ ɫɧɚɱɚɥɚ, ɜɥɢɹɧɢɟ ɚɦɩɥɢɬɭɞɵ ɜɨɡɛɭɠɞɟɧɢɹ

U

ɜɯ

. ɉɪɟɞ-

ɩɨɥɨɠɢɦ, ɱɬɨ

E

ɉ

,

E

ɫɦ

, ɢ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɧɚɝɪɭɡɤɢ

R

ɧ

ɡɚɞɚɧɵ, ɚ

U

ɜɯ

ɜɨɡɪɚɫɬɚɟɬ,

ɧɚɱɢɧɚɹ ɫ ɧɭɥɹ. ɉɪɢ ɷɬɨɦ, ɤɚɤ ɜɢɞɧɨ ɢɡ ɪɢɫ. 1.8, ɜɨɡɪɚɫɬɚɟɬ ɚɦɩɥɢɬɭɞɚ ɢɦɩɭɥɶɫɚ

ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ. Ɉɞɧɚɤɨ ɞɥɹ ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ ɜɚɠɧɟɟ ɜɵɹɜɢɬɶ ɡɚɜɢɫɢɦɨɫɬɶ

ɚɦɩɥɢɬɭɞɵ ɟɝɨ 1-ɣ ɝɚɪɦɨɧɢɤɢ ɨɬ

U

ɜɯ

. ɉɪɢ

ɦɚɥɵɯ

U

ɜɯ

, ɤɨɝɞɚ Ⱥɗ ɟɳɺ ɧɚɯɨɞɢɬɫɹ ɜ ɇɊ,

ɢɡ (1.6) ɢ ɪɢɫ 1.8 ɫɥɟɞɭɟɬ:

I

ɜɵɯ1

= I

ɜɵɯ max

α

1

(

θ

) =

= S U

ɜɯ

(1 – cos

θ

)

α

1

(

θ

),

ɬɨ ɟɫɬɶ,

I

ɜɵɯ1

= S U

ɜɯ

γ

1

(

θ

),

(1.12)

ɝɞɟ

γ

1

(

θ

) —

ɤɨɷɮɮɢɰɢɟɧɬ Ȼɟɪɝɚ.

Ɉɬɫɸɞɚ ɜɢɞɧɨ, ɱɬɨ

I

ɜɵɯ1

ɡɚɜɢɫɢɬ ɧɟ

ɬɨɥɶɤɨ ɨɬ ɚɦɩɥɢɬɭɞɵ ɜɨɡɛɭɠɞɟɧɢɹ

U

ɜɯ

, ɧɨ

ɢ ɨɬ ɭɝɥɚ ɨɬɫɟɱɤɢ

θ

, ɤɨɬɨɪɵɣ, ɤɚɤ ɫɥɟɞɭɟɬ

ɢɡ (1.10), ɬɚɤɠɟ ɡɚɜɢɫɢɬ ɨɬ

U

ɜɯ

. ɉɨɷɬɨɦɭ

ɜɨɡɦɨɠɧɵ ɬɪɢ ɮɨɪɦɵ ɡɚɜɢɫɢɦɨɫɬɢ

I

ɜɵɯ1

(U

ɜɯ

)

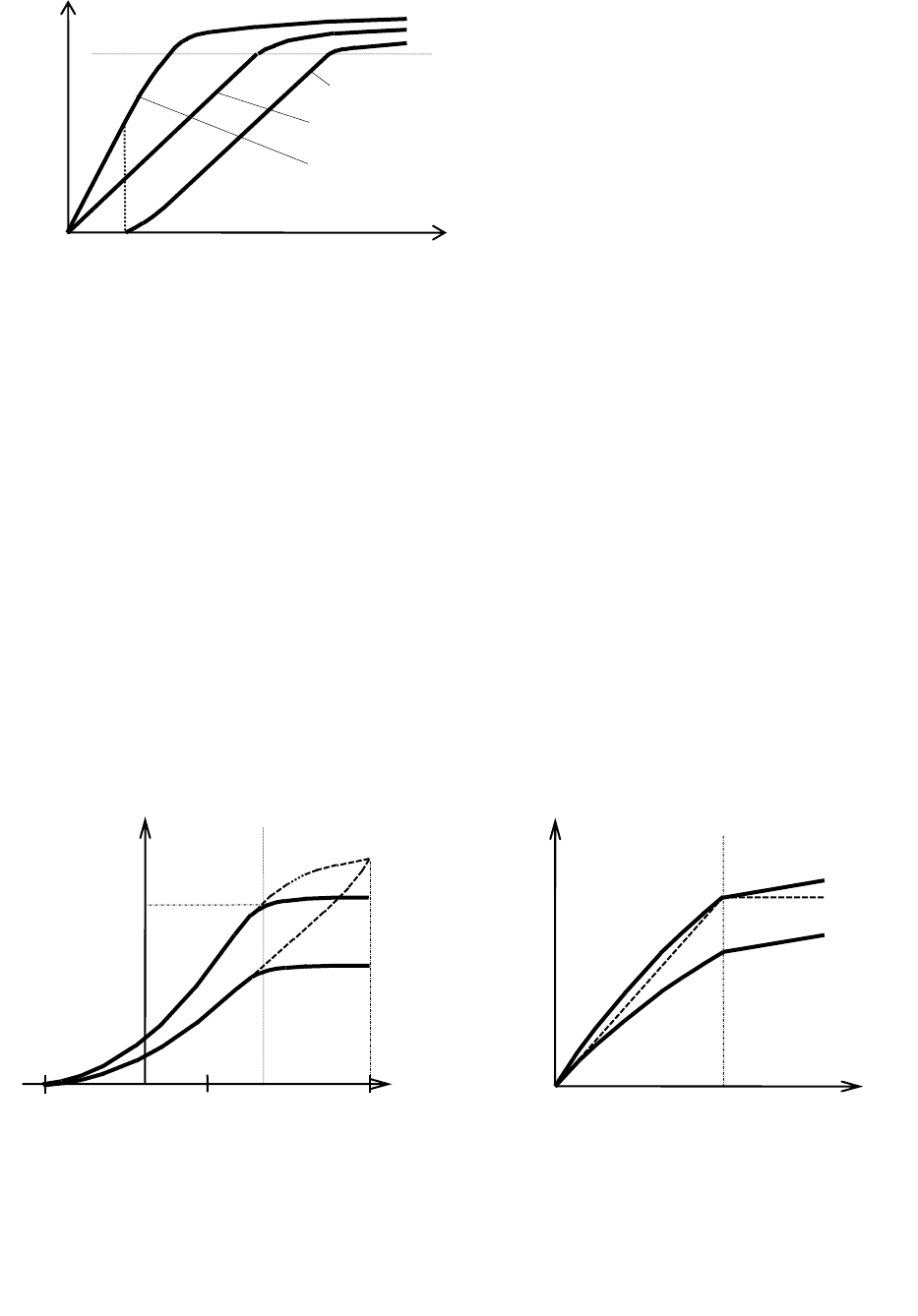
, ɩɨɤɚɡɚɧɧɵɟ ɧɚ ɪɢɫ. 1.9.

i

ɜɵɯ

i

ɜɵɯ

I

ɜɵɯ max

E

ɫɦ

E

′

U

ɜɯ

τ

U

ɜɯ

cos(

θ

)

U

ɜɯ

τ

U

ɜɯ

(1 – cos

θ

)

Ɋɢɫ. 1.8. ɉɨɫɬɪɨɟɧɢɹ ɞɥɹ

ɜɵɱɢɫɥɟɧɢɹ

I

ɜɵɯ

max

14

ɇɚɢɛɨɥɟɟ ɩɪɨɫɬɚɹ ɮɨɪɦɚ ɩɨɥɭɱɚɟɬɫɹ ɩɪɢ

E

ɫɦ

=

E

′

. ȼ ɷɬɨɦ ɫɥɭɱɚɟ

θ

= 90

ɨ

,

γ

1

(90

ɨ

) = 0,5

ɢ ɩɨɷɬɨɦɭ

I

ɜɵɯ1

= 0,5 S U

ɜɯ

.

(1.13)

Ⱥɦɩɥɢɬɭɞɚ 1-ɣ ɝɚɪɦɨɧɢɤɢ ɬɨɤɚ

ɭɜɟɥɢɱɢɜɚɟɬɫɹ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ

U

ɜɯ

. ɉɪɢ ɞɚɥɶɧɟɣɲɟɦ ɜɨɡɪɚɫɬɚɧɢɢ

U

ɜɯ

Ⱥɗ ɩɟɪɟɯɨɞɢɬ ɜ ɉɊ, ɜ ɢɦ-

ɩɭɥɶɫɟ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ ɩɨɹɜɥɹɟɬɫɹ

ɩɪɨɜɚɥ, ɢ ɬɨɤ ɩɟɪɟɫɬɚɟɬ ɪɚɫɬɢ.

ȿɫɥɢ

E

ɫɦ

>

E

′

, ɬɨ ɩɪɢ ɦɚɥɵɯ

ɚɦɩɥɢɬɭɞɚɯ

U

ɜɯ

<

E

ɫɦ

−

E

′

. ɨɬɫɟɱɤɢ

ɧɟɬ ɢ

I

ɜɵɯ1

= S U

ɜɯ

; ɩɨɫɥɟ ɩɨɹɜ-

ɥɟɧɢɹ ɨɬɫɟɱɤɢ ɭɝɨɥ

θ

→ 90

ɨ

ɩɪɢ

U

ɜɯ

→ ∞

. ɋɨɝɥɚɫɧɨ (1.12) ɭɦɟɧɶ-

ɲɟɧɢɟ

θ

ɩɪɢɜɟɞɟɬ ɤ ɭɦɟɧɶɲɟɧɢɸ

ɤɪɭɬɢɡɧɵ ɡɚɜɢɫɢɦɨɫɬɢ

I

ɜɵɯ1

(U

ɜɯ

)

,

ɧɨ ɷɬɚ ɤɪɭɬɢɡɧɚ ɜɫɟɝɞɚ ɛɨɥɶɲɟ, ɱɟɦ

0,5S

. ɉɨɫɤɨɥɶɤɭ ɩɪɢ

E

ɫɦ

>

E

′

, ɤɚɠɞɨɦɭ

ɡɧɚɱɟɧɢɸ

U

ɜɯ

ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɛɨ′ɥɶɲɢɣ ɢɦɩɭɥɶɫ ɬɨɤɚ, ɱɟɦ ɩɪɢ

E

ɫɦ

=

E

′

, Ⱥɗ

ɩɟɪɟɯɨɞɢɬ ɜ ɉɊ ɩɪɢ ɦɟɧɶɲɟɦ ɡɧɚɱɟɧɢɢ

U

ɜɯ

. ɉɪɢ

E

ɫɦ

<

E

′

ɢ

U

ɜɯ

<

E

ɫɦ

−

E

′

ɬɨɤ

I

ɜɵɯ1

ɨɬɫɭɬɫɬɜɭɟɬ; ɩɨɫɥɟ ɨɬɤɪɵɜɚɧɢɹ Ⱥɗ

I

ɜɵɯ1

ɧɚɪɚɫɬɚɟɬ ɢɡ-ɡɚ ɨɞɧɨɜɪɟɦɟɧɧɨɝɨ

ɭɜɟɥɢɱɟɧɢɹ

U

ɜɯ

ɢ

θ

ɢ ɨɫɬɚɟɬɫɹ ɩɨɫɬɨɹɧɧɵɦ ɜ ɉɊ.

ɉɟɪɟɣɞɟɦ ɤ ɢɡɭɱɟɧɢɸ ɜɥɢɹɧɢɹ ɧɚɩɪɹɠɟɧɢɹ ɫɦɟɳɟɧɢɹ

E

ɫɦ

ɧɚ ɪɟɠɢɦ

ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ. ɉɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ

U

ɜɯ

, ɢ

E

ɉ

ɩɨɫɬɨɹɧɧɵ. ȼ ɇɊ ɢɡɦɟɧɟɧɢɟ

E

ɫɦ

ɩɪɢɜɨɞɢɬ ɤ ɢɡɦɟɧɟɧɢɸ ɭɝɥɚ ɨɬɫɟɱɤɢ

θ

. ɂɡ (1.10) ɫɥɟɞɭɟɬ, ɱɬɨ

–cos

θ

ɢ

I

ɜɵɯ1

I

ɜɵɯ0

I

ɜɵɯ1

I

ɜɵɯ0

ɇɊ ɉɊ ɉɊ ɇɊ

I

ɜɵɯ1

I

ɜɵɯ1

I

ɜɵɯ0

I

ɜɵɯ0

E

ɫɦ

E

ɉ

E

′−

U

ɜɯ

E

′

E

′

+U

ɜɯ

E

ɉ ɤɪ

I

ɜɵɯ1

I

ɜɵɯ ɤɪ

E

ɫɦ

<

E

′

.

E

ɫɦ

=

E

′

.

E

ɫɦ

>

E

′

.

|E

ɫɦ

–

E

′

| U

ɜɯ

Ɋɢɫ. 1.9. Ɂɚɜɢɫɢɦɨɫɬɶ ɚɦɩɥɢɬɭɞɵ 1-ɣ

ɝɚɪɦɨɧɢɤɢ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ ɨɬ ɚɦɩɥɢ-

ɬɭɞɵ ɜɨɡɛɭɠɞɟɧɢɹ

Ɋɢɫ. 1.10. Ɂɚɜɢɫɢɦɨɫɬɶ ɚɦɩɥɢɬɭɞɵ

1-ɣ ɝɚɪɦɨɧɢɤɢ ɢ ɩɨɫɬɨɹɧɧɨɣ ɫɨɫ-

ɬɚɜɥɹɸɳɟɣ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ ɨɬ

ɧɚɩɪɹɠɟɧɢɹ ɫɦɟɳɟɧɢɹ ȿ

ɫɦ

Ɋɢɫ. 1.11. Ɂɚɜɢɫɢɦɨɫɬɶ ɚɦɩɥɢɬɭɞɵ

1-ɣ ɝɚɪɦɨɧɢɤɢ ɢ ɩɨɫɬɨɹɧɧɨɣ ɫɨɫ-

ɬɚɜɥɹɸɳɟɣ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ ɨɬ

ɧɚɩɪɹɠɟɧɢɹ ɩɢɬɚɧɢɹ ȿ

ɉ

15

E

ɫɦ

ɫɜɹɡɚɧɵ ɥɢɧɟɣɧɨ, ɩɨɷɬɨɦɭ ɜɵɯɨɞɧɵɟ ɯɚɪɚɤɬɟɪɢɫɬɢɤɢ

I

ɜɵɯ1

(E

ɫɦ

)

ɢ

I

ɜɵɯ0

(E

ɫɦ

)

ɛɭɞɭɬ ɩɨɜɬɨɪɹɬɶ ɜ ɢɧɨɦ ɦɚɫɲɬɚɛɟ ɮɭɧɤɰɢɢ

γ

1

(−cos

θ

)

ɢ

γ

0

(−cos

θ

))

ɞɨ ɬɟɯ ɩɨɪ,

ɩɨɤɚ Ⱥɗ ɧɟ ɩɟɪɟɣɞɟɬ ɜ ɉɊ (ɫɦ. ɪɢɫ. 1.10).

ɉɪɟɞɩɨɥɨɠɢɦ ɬɟɩɟɪɶ, ɱɬɨ

E

ɫɦ

,

U

ɜɯ

ɢ

R

ɧ

ɩɨɫɬɨɹɧɧɵ ɚ

E

ɉ

ɢɡɦɟɧɹɟɬɫɹ.

ɉɪɢ ɛɨɥɶɲɢɯ

E

ɉ

Ⱥɗ ɧɚɯɨɞɢɬɫɹ ɜ ɇɊ, ɩɨɷɬɨɦɭ ɜɵɫɨɬɚ ɢ ɮɨɪɦɚ ɢɦɩɭɥɶɫɚ

ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ ɛɭɞɭɬ ɨɩɪɟɞɟɥɹɬɶɫɹ ɬɨɥɶɤɨ ɡɧɚɱɟɧɢɟɦ

U

ɜɯ

. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɬɨɤɢ

I

ɜɵɯ1

,

I

ɜɵɯ0

ɛɭɞɭɬ ɩɨɱɬɢ ɩɨɫɬɨɹɧɧɵɦɢ. ɉɪɢ ɭɦɟɧɶɲɟɧɢɢ

E

ɉ

ɜ ɢɦɩɭɥɶɫɟ ɬɨɤɚ

ɩɨɹɜɥɹɟɬɫɹ ɩɪɨɜɚɥ ɢ ɚɦɩɥɢɬɭɞɚ 1-ɣ ɝɚɪɦɨɧɢɤɢ ɬɨɤɚ

I

ɜɵɯ1

ɜɦɟɫɬɟ ɫ

I

ɜɵɯ0

ɭɛɵɜɚɸɬ. ɋɥɟɞɭɟɬ ɨɬɦɟɬɢɬɶ, ɱɬɨ ɡɚɜɢɫɢɦɨɫɬɶ

I

ɜɵɯ1

(

E

ɉ

) ɛɥɢɡɤɚ ɤ ɥɢɧɟɣɧɨɣ.

1.6. ȼɵɛɨɪ ɭɝɥɚ ɨɬɫɟɱɤɢ ɭɫɢɥɢɬɟɥɹ ɦɨɳɧɨɫɬɢ

Ʉɚɤ ɩɪɚɜɢɥɨ, Ⱥɗ ɜ ɭɫɢɥɢɬɟɥɹɯ ɦɨɳɧɨɫɬɢ ɪɚɛɨɬɚɸɬ ɜ ɤɪɢɬɢɱɟɫɤɨɦ ɪɟ-

ɠɢɦɟ, ɤɚɤ ɧɚɢɛɨɥɟɟ ɷɧɟɪɝɟɬɢɱɟɫɤɢ ɜɵɝɨɞɧɨɦ. Ʉɨɧɤɪɟɬɧɵɟ ɠɟ ɷɧɟɪɝɟɬɢɱɟɫɤɢɟ

ɩɚɪɚɦɟɬɪɵ ɛɭɞɭɬ ɜɨ ɦɧɨɝɨɦ ɨɩɪɟɞɟɥɹɬɶɫɹ ɜɵɛɨɪɨɦ ɡɧɚɱɟɧɢɹ ɭɝɥɚ ɨɬɫɟɱɤɢ

θ

.

Ʉɚɤ ɛɵɥɨ ɩɨɤɚɡɚɧɨ ɜ ɩ. 1.2 ɭɦɟɧɶɲɟɧɢɟ ɭɝɥɚ ɨɬɫɟɱɤɢ

θ

ɩɪɢɜɨɞɢɬ ɤ

ɭɜɟɥɢɱɟɧɢɸ ɷɥɟɤɬɪɨɧɧɨɝɨ ɄɉȾ

η

ɷ

. Ɉɞɧɚɤɨ ɭɱɟɬ ɪɟɚɥɶɧɵɯ ɯɚɪɚɤɬɟɪɢɫɬɢɤ Ⱥɗ

ɩɨɤɚɡɵɜɚɟɬ, ɱɬɨ ɦɚɥɵɟ ɡɧɚɱɟɧɢɹ

θ

ɬɚɤɠɟ ɷɧɟɪɝɟɬɢɱɟɫɤɢ ɧɟɜɵɝɨɞɧɵ. Ʉɚɤɨɟ ɡɧɚ-

ɱɟɧɢɟ

θ

ɦɨɠɧɨ ɫɱɢɬɚɬɶ ɨɩɬɢɦɚɥɶɧɵɦ? ɗɬɨ ɡɚɜɢɫɢɬ ɨɬ ɯɚɪɚɤɬɟɪɚ ɩɨɫɬɚɧɨɜɤɢ

ɡɚɞɚɱɢ.

1. Ɋɚɫɱɟɬ ɧɚ ɦɚɤɫɢɦɚɥɶɧɭɸ ɜɵɯɨɞɧɭɸ ɦɨɳɧɨɫɬɶ. ɉɭɫɬɶ ɜɵɛɪɚɧ ɬɢɩ Ⱥɗ

ɢ ɨɩɪɟɞɟɥɟɧɨ ɧɚɩɪɹɠɟɧɢɟ ɩɢɬɚɧɢɹ

E

ɉ

ɢ ɬɪɟɛɭɟɬɫɹ ɩɨɥɭɱɢɬɶ ɦɚɤɫɢɦɚɥɶɧɭɸ

ɜɵɯɨɞɧɭɸ ɦɨɳɧɨɫɬɶ

P

1

. ɗɬɨ ɜɨɡɦɨɠɧɨ ɩɪɢ ɩɨɥɧɨɦ ɢɫɩɨɥɶɡɨɜɚɧɢɢ Ⱥɗ ɩɨ ɬɨɤɭ,

ɬ.ɟ.

i

ɜɵɯ max

=

I

ɜɵɯ ɞɨɩ

, ɝɞɟ

I

ɜɵɯ ɞɨɩ

— ɦɚɤɫɢɦɚɥɶɧɨ ɞɨɩɭɫɬɢɦɨɟ ɡɧɚɱɟɧɢɟ ɢɦ-

ɩɭɥɶɫɧɨɝɨ ɬɨɤɚ ɞɥɹ ɞɚɧɧɨɝɨ Ⱥɗ. ɉɪɢ ɷɬɢɯ ɭɫɥɨɜɢɹɯ ɧɚɢɛɨɥɶɲɚɹ ɚɦɩɥɢɬɭɞɚ 1-ɣ

ɝɚɪɦɨɧɢɤɢ ɬɨɤɚ ɩɨɥɭɱɚɟɬɫɹ ɩɪɢ

θ

= 120

ɨ

. Ɉɞɧɚɤɨ, ɟɫɥɢ ɭɦɟɧɶɲɢɬɶ ɭɝɨɥ

ɨɬɫɟɱɤɢ ɞɨ

θ

= 90

ɨ

, ɬɨ ɦɨɳɧɨɫɬɶ

P

1

ɭɩɚɞɟɬ ɦɟɧɶɲɟ ɱɟɦ ɧɚ 7%, ɡɚɬɨ ɄɉȾ ɭɜɟ-

ɥɢɱɢɬɫɹ (ɩɪɢ

ξ ≈

0,9

) ɫ 0,6 ɞɨ 0,71 ɢ, ɱɬɨ ɫɚɦɨɟ ɝɥɚɜɧɨɟ, ɦɨɳɧɨɫɬɶ,

ɪɚɫɫɟɢɜɚɟɦɚɹ Ⱥɗ, ɫɧɢɡɢɬɫɹ ɩɨɱɬɢ ɜ ɩɨɥɬɨɪɚ ɪɚɡɚ. ɉɨɷɬɨɦɭ ɞɥɹ ɞɚɧɧɨɣ

ɩɨɫɬɚɧɨɜɤɢ ɡɚɞɚɱɢ ɭɝɨɥ ɨɬɫɟɱɤɢ

θ

= 90

ɨ

ɫɱɢɬɚɟɬɫɹ ɨɩɬɢɦɚɥɶɧɵɦ.

2. Ɋɚɫɱɟɬ ɧɚ ɡɚɞɚɧɧɭɸ ɜɵɯɨɞɧɭɸ ɦɨɳɧɨɫɬɶ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɡɚɞɚɧɵ ɬɢɩ

Ⱥɗ, ɧɚɩɪɹɠɟɧɢɟ ɩɢɬɚɧɢɹ

E

ɉ

ɢ ɬɪɟɛɭɟɦɚɹ ɜɵɯɨɞɧɚɹ ɦɨɳɧɨɫɬɶ

P

1.

.

ɉɪɟɞ-

ɩɨɥɨɠɢɦ ɫɧɚɱɚɥɚ, ɱɬɨ ɨɝɪɚɧɢɱɟɧɢɟ ɧɚ

I

ɜɵɯ ɞɨɩ

ɨɬɫɭɬɫɬɜɭɟɬ ɢ ɪɚɫɫɦɨɬɪɢɦ, ɤɚɤ

ɦɟɧɹɟɬɫɹ

η

ɷ

ɩɪɢ ɢɡɦɟɧɟɧɢɢ

θ

, ɟɫɥɢ

P

1

ɮɢɤɫɢɪɨɜɚɧɨ. ɉɪɢ ɭɦɟɧɶɲɟɧɢɢ

θ

ɚɦɩɥɢɬɭɞɚ ɩɟɪɜɨɣ ɝɚɪɦɨɧɢɤɢ ɜɵɯɨɞɧɨɝɨ ɬɨɤɚ

I

ɜɵɯ1

ɫɧɢɠɚɟɬɫɹ. Ⱦɥɹ ɬɨɝɨ ɱɬɨɛɵ

ɜɵɯɨɞɧɚɹ ɦɨɳɧɨɫɬɶ ɩɪɢ ɷɬɨɦ ɧɟ ɫɧɢɠɚɥɚɫɶ, ɧɟɨɛɯɨɞɢɦɨ ɭɜɟɥɢɱɢɜɚɬɶ

ɚɦɩɥɢɬɭɞɭ ɜɵɯɨɞɧɨɝɨ ɢɦɩɭɥɶɫɚ

i

ɜɵɯ max

, ɱɬɨ, ɤɚɤ ɜɢɞɧɨ ɢɡ ɩɨɫɬɪɨɟɧɢɣ ɧɚ

ɪɢɫ. 1.12, ɩɪɢɜɨɞɢɬ ɤ ɫɧɢɠɟɧɢɸ

ξ

ɤɪ

. ɉɨɷɬɨɦɭ ɄɉȾ ɫɨɝɥɚɫɧɨ (1.5) ɩɪɢ

ɭɦɟɧɶɲɟɧɢɢ

θ

ɫɧɚɱɚɥɚ ɜɨɡɪɚɫɬɚɟɬ, ɩɨɫɤɨɥɶɤɭ

ξ

ɤɪ

ɩɨɱɬɢ ɧɟ ɢɡɦɟɧɹɟɬɫɹ, ɚ

16

i

ɜɵɯ

i

ɜɵɯ

i

ɜɵɯ

i

′′

ɜɵɯ max

i

′

ɜɵɯ max

E

′′

ɫɦ

E

′

ɫɦ

u

ɜɯ

E

ɉ

u

ɜɵɯ

2

θ′′

u

ɜɯ

2

θ′

u

ɜɵɯ

E

′′

ɫɦ

– U

ɜɯ

τ

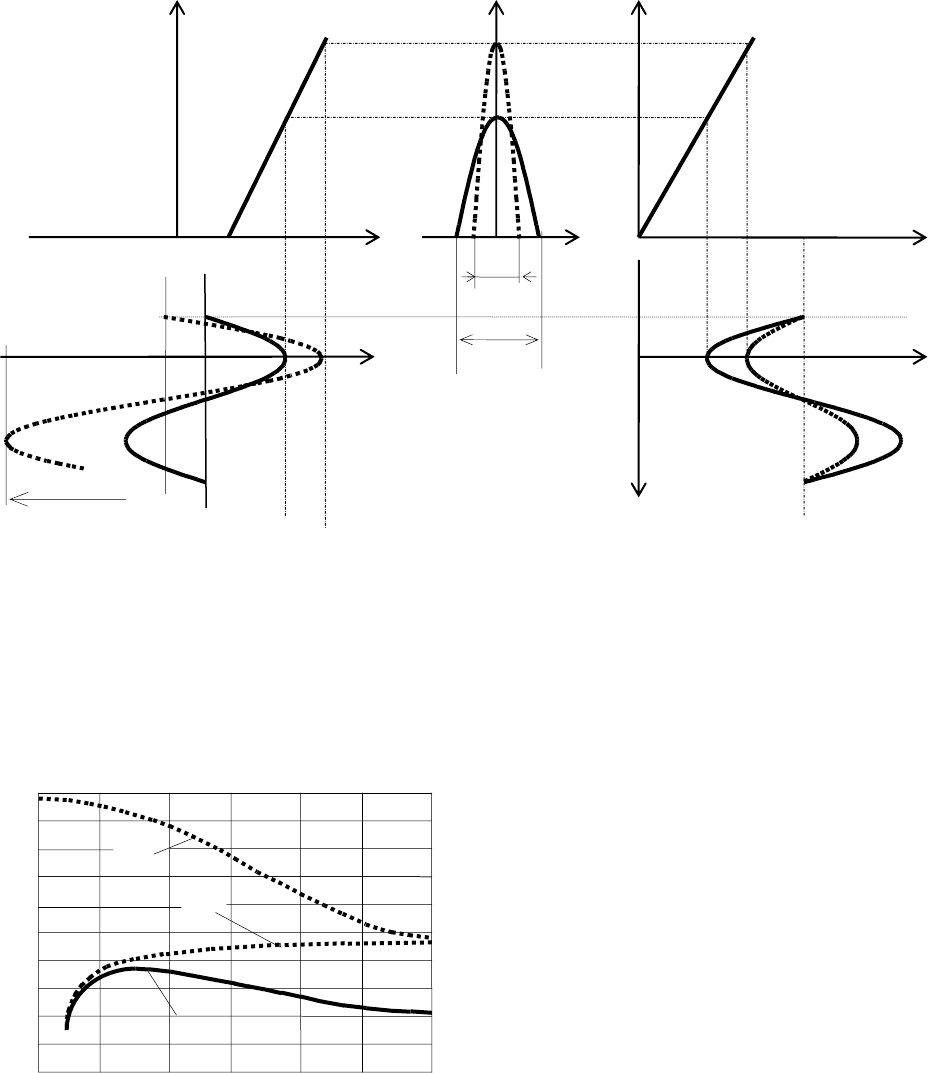
Ɋɢɫ. 1.12. ɂɦɩɭɥɶɫɵ ɬɨɤɚ ɢ ɧɚɩɪɹɠɟɧɢɹ ɧɚ Ⱥɗ ɩɪɢ ɞɜɭɯ ɡɧɚɱɟɧɢɹɯ ɭɝɥɚ ɨɬ-

ɫɟɱɤɢ ɢ ɩɨɫɬɨɹɧɧɨɣ ɦɨɳɧɨɫɬɢ

P

1

.

g

1

(

θ

)

ɪɚɫɬɟɬ (ɪɢɫ. 1.13). Ɉɞɧɚɤɨ ɩɪɢ

θ

< 70…80

ɨ

ɭɜɟɥɢɱɟɧɢɟ

g

1

(

θ

)

ɭɠɟ ɧɟɡɧɚ-

ɱɢɬɟɥɶɧɨ, ɚ ɩɚɞɟɧɢɟ

ξ

ɤɪ

, ɜɵɡɜɚɧɧɨɟ ɪɨɫɬɨɦ

i

ɜɵɯ max

ɫɬɚɧɨɜɢɬɫɹ ɛɵɫɬɪɵɦ.

ɉɨɷɬɨɦɭ ɜ ɨɛɥɚɫɬɢ ɦɚɥɵɯ ɭɝɥɨɜ

θ

ɭɦɟɧɶɲɟɧɢɟ ɭɝɥɚ ɨɬɫɟɱɤɢ ɜɵɡɵɜɚɟɬ

ɭɦɟɧɶɲɟɧɢɟ ɄɉȾ. Ɇɚɤɫɢɦɚɥɶɧɨɟ ɡɧɚɱɟ-

ɧɢɟ

η

ɷ

ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɭɝɥɭ ɨɬɫɟɱɤɢ,

ɥɟɠɚɳɟɦɭ ɜ ɩɪɟɞɟɥɚɯ ɨɬ 50 ɞɨ 80

ɨ

ɢ

ɡɚɜɢɫɢɬ ɨɬ

S

ɤɪ

ɢ

E

ɉ

.

ɂɡ ɪɢɫ. 1.12 ɜɢɞɧɨ, ɱɬɨ ɭɦɟɧɶɲɟɧɢɟ

θ

ɫɨɩɪɨɜɨɠɞɚɟɬɫɹ ɪɨɫɬɨɦ

i

ɜɵɯ max

, ɩɪɢɱɟɦ

ɩɪɟɞɟɥɶɧɨɟ ɡɧɚɱɟɧɢɟ

I

ɜɵɯ ɞɨɩ

ɦɨɠɟɬ

ɛɵɬɶ ɞɨɫɬɢɝɧɭɬɨ ɪɚɧɶɲɟ, ɱɟɦ

ɨɩɬɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ

θ

. ɋ ɞɪɭɝɨɣ ɫɬɨ-

ɪɨɧɵ, ɫ ɭɦɟɧɶɲɟɧɢɟɦ

θ

ɪɚɫɬɟɬ ɦɚɤɫɢ-

ɦɚɥɶɧɨɟ ɨɛɪɚɬɧɨɟ ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɜɯɨɞɟ.

Ɂɧɚɱɟɧɢɟ

θ

, ɩɪɢ ɤɨɬɨɪɨɦ |

E

ɫɦ

−

U

ɜɯ

|

ɫɬɚɧɨɜɢɬɫɹ ɛɨɥɶɲɟ ɞɨɩɭɫɬɢɦɨɝɨ, ɬɚɤɠɟ ɦɨɠɟɬ ɨɤɚɡɚɬɶɫɹ ɛɨɥɶɲɟ ɨɩɬɢɦɚɥɶɧɨɝɨ.

Ʉɪɨɦɟ ɬɨɝɨ, ɫ ɭɦɟɧɶɲɟɧɢɟɦ

θ

ɪɚɫɬɟɬ ɧɚɩɪɹɠɟɧɢɟ ɜɨɡɛɭɠɞɟɧɢɹ

U

ɜɯ

, ɱɬɨ ɜ

ɪɟɚɥɶɧɵɯ ɤɚɫɤɚɞɚɯ ɫɧɢɠɚɟɬ ɨɛɳɢɣ ɤɨɷɮɮɢɰɢɟɧɬ ɭɫɢɥɟɧɢɹ ɩɨ ɦɨɳɧɨɫɬɢ.

ɍɱɢɬɵɜɚɹ ɢɡɥɨɠɟɧɧɨɟ, ɪɟɤɨɦɟɧɞɭɟɬɫɹ ɜɵɛɢɪɚɬɶ ɭɝɨɥ ɨɬɫɟɱɤɢ ɜ ɢɧɬɟɪɜɚɥɟ

75...90

ɨ

.

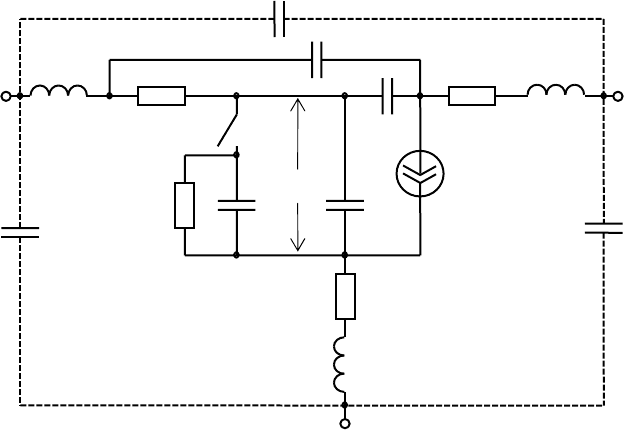
η

ɷ

,

ξ

, g

1

2.0

1.6

g

1

1.2

ξ

0.8

0.4

η

ɷ

0 30 60 90 120 150

θ

ɨ

Ɋɢɫ. 1.13. Ɂɚɜɢɫɢɦɨɫɬɶ ɄɉȾ Ⱥɗ ɨɬ

ɭɝɥɚ ɨɬɫɟɱɤɢ

17

Ƚɥɚɜɚ 2. ɌɊȺɇɁɂɋɌɈɊɇɕȿ ɍɋɂɅɂɌȿɅɂ ɆɈɓɇɈɋɌɂ

ȼ ɝɥɚɜɟ 1 ɛɵɥɢ ɪɚɫɫɦɨɬɪɟɧɵ ɫɚɦɵɟ ɨɛɳɢɟ ɫɜɨɣɫɬɜɚ Ƚȼȼ ɧɚ ɩɪɢɦɟɪɟ

ɚɛɫɬɪɚɤɬɧɨɝɨ ɛɟɡɵɧɟɪɰɢɨɧɧɨɝɨ Ⱥɗ. ɉɪɢɦɟɪɨɦ ɪɟɚɥɶɧɨɝɨ Ƚȼȼ, ɨɛɥɚɞɚɸɳɢɦ

ɹɪɤɨ ɜɵɪɚɠɟɧɧɵɦɢ ɢɧɟɪɰɢɨɧɧɵɦɢ ɫɜɨɣɫɬɜɚɦɢ ɹɜɥɹɟɬɫɹ, ɬɪɚɧɡɢɫɬɨɪɧɵɣ ɭɫɢ-

ɥɢɬɟɥɶ ɦɨɳɧɨɫɬɢ (ɌɍɆ). ɍɫɢɥɢɬɟɥɶɧɵɟ ɭɫɬɪɨɣɫɬɜɚ ɧɚ ɬɪɚɧɡɢɫɬɨɪɚɯ

ɪɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɜ ɪɚɡɥɢɱɧɵɯ ɤɭɪɫɚɯ, ɩɨɷɬɨɦɭ ɧɟɬ ɫɦɵɫɥɚ ɢɡɭɱɚɬɶ ɢɯ ɨɛɳɭɸ

ɬɟɨɪɢɸ. ɐɟɥɶ ɞɚɧɧɨɝɨ ɪɚɡɞɟɥɚ — ɢɡɭɱɟɧɢɟ ɨɫɨɛɟɧɧɨɫɬɟɣ ɌɍɆ ɜ ɦɨɳɧɵɯ

ɤɚɫɤɚɞɚɯ ɪɚɞɢɨɷɥɟɤɬɪɨɧɧɵɯ ɭɫɬɪɨɣɫɬɜ ɧɚ ɜɵɫɨɤɢɯ ɱɚɫɬɨɬɚɯ. Ɇɨɠɧɨ ɜɵɞɟɥɢɬɶ

ɫɥɟɞɭɸɳɢɟ ɨɫɨɛɟɧɧɨɫɬɢ ɪɚɛɨɬɵ ɬɪɚɧɡɢɫɬɨɪɚ ɜ ɭɫɢɥɢɬɟɥɹɯ ɦɨɳɧɨɫɬɢ:

• ɧɟɥɢɧɟɣɧɵɣ ɪɟɠɢɦ, ɢɥɢ ɪɟɠɢɦ ɛɨɥɶɲɨɝɨ ɫɢɝɧɚɥɚ;

• ɛɨɥɶɲɚɹ ɜɵɯɨɞɧɚɹ ɦɨɳɧɨɫɬɶ;

• ɜɵɫɨɤɚɹ ɱɚɫɬɨɬɚ.

ɉɨɫɤɨɥɶɤɭ ɬɨɱɧɨ ɨɩɢɫɚɬɶ ɪɚɛɨɬɭ ɬɪɚɧɡɢɫɬɨɪɚ ɩɪɚɤɬɢɱɟɫɤɢ ɧɟɜɨɡɦɨɠɧɨ ɢɡ-ɡɚ

ɫɥɨɠɧɨɫɬɢ ɩɪɨɬɟɤɚɸɳɢɯ ɜ ɧɟɦ ɩɪɨɰɟɫɫɨɜ, ɨɛɵɱɧɨ ɩɪɢɦɟɧɹɸɬ ɤɚɤɭɸ-ɥɢɛɨ

ɭɩɪɨɳɟɧɧɭɸ ɦɨɞɟɥɶ, ɩɪɢɛɥɢɠɟɧɧɨ ɨɩɢɫɵɜɚɸɳɭɸ ɪɚɛɨɬɭ ɬɪɚɧɡɢɫɬɨɪɚ.

2.1.

Ɇɨɞɟɥɶ ɦɨɳɧɨɝɨ ɛɢɩɨɥɹɪɧɨɝɨ ɬɪɚɧɡɢɫɬɨɪɚ

ɂɡɜɟɫɬɧɨ ɧɟɫɤɨɥɶɤɨ ɦɨɞɟɥɟɣ ɛɢɩɨɥɹɪɧɵɯ ɬɪɚɧɡɢɫɬɨɪɨɜ, ɨɫɧɨɜɧɨɟ

ɪɚɡɥɢɱɢɟ ɦɟɠɞɭ ɤɨɬɨɪɵɦɢ ɫɜɹɡɚɧɨ ɫɨ ɫɩɨɫɨɛɨɦ ɨɩɢɫɚɧɢɹ ɷɤɜɢɜɚɥɟɧɬɧɨɝɨ

ɝɟɧɟɪɚɬɨɪɚ ɬɨɤɚ. Ɇɵ ɛɭɞɟɦ ɢɫɩɨɥɶɡɨɜɚɬɶ ɦɨɞɟɥɶ Ⱦɠɢɚɤɨɥɟɬɬɨ, ɜ ɤɨɬɨɪɨɣ ɬɨɤ

ɝɟɧɟɪɚɬɨɪɚ

i

ɝ

= S

ɉ

u

ɉ

, ɝɞɟ

u

ɉ

— ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɩɟɪɟɯɨɞɟ ɛɚɡɚ-ɷɦɢɬɬɟɪ.

Ȼɢɩɨɥɹɪɧɵɣ ɬɪɚɧɡɢɫɬɨɪ ɦɨɠɟɬ ɪɚɛɨɬɚɬɶ ɜ ɱɟɬɵɪɟɯ ɪɟɠɢɦɚɯ: ɚɤɬɢɜɧɨɦ,

ɨɬɫɟɱɤɢ, ɧɚɫɵɳɟɧɢɹ ɢ ɢɧɜɟɪɫɢɢ. ɉɨɫɥɟɞɧɢɣ ɪɟɠɢɦ ɜ ɌɍɆ ɧɟ ɢɫɩɨɥɶɡɭɟɬɫɹ,

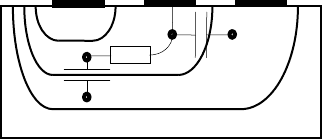
ɩɨɷɬɨɦɭ ɷɤɜɢɜɚɥɟɧɬɧɚɹ ɫɯɟɦɚ ɬɪɚɧɡɢɫɬɨɪɚ ɢɦɟɟɬ ɜɢɞ, ɩɨɤɚɡɚɧɧɵɣ ɧɚ ɪɢɫ. 2.1.

C

ɤɛ

C

ɤɩ

Ȼ

L

ɛ

r

ɛ

r

ɤ

L

ɤ

Ʉ

ɥ

C

ɤɚ

C

ɞ

u

ɩ

i

ɝ

C

ɛɷ

r

β

C

ɷ

C

ɤɷ

r

ɷ

L

ɷ

ɗ

Ɋɢɫ 2.1. ɗɤɜɢɜɚɥɟɧɬɧɚɹ ɫɯɟɦɚ ɛɢɩɨɥɹɪɧɨɝɨ ɬɪɚɧɡɢɫɬɨɪɚ

18

ɇɚ ɷɤɜɢɜɚɥɟɧɬɧɨɣ ɫɯɟɦɟ ɢɫɩɨɥɶɡɭɸɬɫɹ ɫɥɟɞɭɸɳɢɟ ɨɛɨɡɧɚɱɟɧɢɹ:

L

ɛ

, L

ɤ

, L

ɷ

— ɢɧɞɭɤɬɢɜɧɨɫɬɢ ɜɵɜɨɞɨɜ;

r

ɛ

, r

ɤ

, r

ɷ

— ɨɦɢɱɟɫɤɢɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɦɚɬɟɪɢɚɥɚ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɛɚɡɵ,

ɤɨɥɥɟɤɬɨɪɚ ɢ ɷɦɢɬɬɟɪɚ;

C

ɷ

— ɺɦɤɨɫɬɶ ɡɚɩɟɪɬɨɝɨ ɷɦɢɬɬɟɪɧɨɝɨ ɩɟɪɟɯɨɞɚ:

C

ɞ

— ɞɢɮɮɭɡɢɨɧɧɚɹ ɺɦɤɨɫɬɶ ɷɦɢɬɬɟɪɧɨɝɨ ɩɟɪɟɯɨɞɚ;

r

β

— ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɪɟɤɨɦɛɢɧɚɰɢɢ;

C

ɤɚ

,

C

ɤɩ

— ɺɦɤɨɫɬɢ ɚɤɬɢɜɧɨɣ ɢ ɩɚɫɫɢɜɧɨɣ ɱɚɫɬɟɣ ɤɨɥɥɟɤɬɨɪɧɨɝɨ

ɩɟɪɟɯɨɞɚ, ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ;

C

ɤɷ

,

C

ɤɛ

,

C

ɛɷ

, — ɩɚɪɚɡɢɬɧɵɟ ɺɦɤɨɫɬɢ ɜɵɜɨɞɨɜ;







′

≤

′

>

′

−

=

,,0

;),(

Eu

EuEuS

i

ɉ

ɉɉɉ

ɝ

(2.1)

ɝɞɟ

E

′

— ɧɚɩɪɹɠɟɧɢɟ ɨɬɫɟɱɤɢ;

u

ɉ

— ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɷɦɢɬɬɟɪɧɨɦ ɩɟɪɟɯɨɞɟ;

S

ɉ

— ɤɪɭɬɢɡɧɚ ɩɨ ɩɟɪɟɯɨɞɭ.

ɉɪɨɢɫɯɨɠɞɟɧɢɟ ɺɦɤɨɫɬɟɣ ɋ

ɤɚ

ɢ ɋ

ɤɩ

ɦɨɠɧɨ ɩɨɧɹɬɶ, ɟɫɥɢ ɨɛɪɚɬɢɬɶɫɹ ɤ

ɤɨɧɫɬɪɭɤɰɢɢ ɦɨɳɧɨɝɨ ɜɵɫɨɤɨɱɚɫɬɨɬɧɨɝɨ ɬɪɚɧɡɢɫɬɨɪɚ, ɤɨɬɨɪɵɣ ɨɛɵɱɧɨ

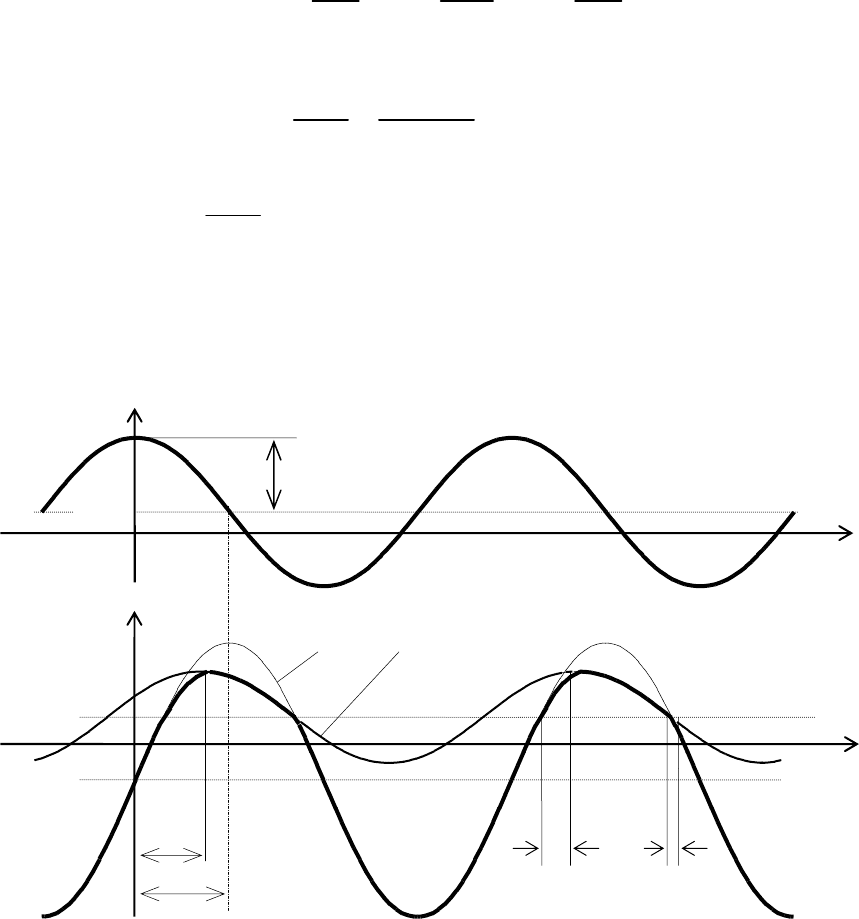
ɜɵɩɨɥɧɹɟɬɫɹ ɩɨ ɩɥɚɧɚɪɧɨɣ ɬɟɯɧɨɥɨɝɢɢ

(ɪɢɫ. 2.2). ɇɚ ɢɫɯɨɞɧɨɣ ɩɨɞɥɨɠɤɟ

ɩɨɥɭɩɪɨɜɨɞɧɢɤɨɜɨɝɨ ɦɚɬɟɪɢɚɥɚ ɩɭɬɟɦ ɫɟɥɟɤ-

ɬɢɜɧɨɝɨ ɥɟɝɢɪɨɜɚɧɢɹ ɩɨɥɭɱɚɸɬ ɧɟɨɛɯɨɞɢɦɵɟ

p ɢ n ɨɛɥɚɫɬɢ. ɉɥɨɳɚɞɶ ɤɨɥɥɟɤɬɨɪɧɨɝɨ ɩɟ-

ɪɟɯɨɞɚ ɩɨɥɭɱɚɟɬɫɹ ɜ 3..5 ɪɚɡ ɛɨɥɶɲɟ ɩɥɨɳɚɞɢ

ɷɦɢɬɬɟɪɧɨɝɨ ɩɟɪɟɯɨɞɚ. ɗɬɚ ɢɡɛɵɬɨɱɧɚɹ ɩɥɨ-

ɳɚɞɶ ɢ ɫɨɡɞɚɟɬ ɩɚɫɫɢɜɧɭɸ ɱɚɫɬɶ ɺɦɤɨɫɬɢ ɤɨɥ-

ɥɟɤɬɨɪɧɨɝɨ ɩɟɪɟɯɨɞɚ. ɉɨɷɬɨɦɭ ɫɩɪɚɜɟɞɥɢɜɨ

ɫɨɨɬɧɨɲɟɧɢɟ C

ɤɚ

= C

ɤɩ

/(3...5).

Ɇɨɳɧɵɟ ɜɵɫɨɤɨɱɚɫɬɨɬɧɵɟ ɬɪɚɧɡɢɫɬɨɪɵ ɞɟɥɚɸɬɫɹ, ɤɚɤ ɩɪɚɜɢɥɨ,

ɦɧɨɝɨɷɦɢɬɬɟɪɧɵɦɢ. Ⱦɥɹ ɜɵɪɚɜɧɢɜɚɧɢɹ ɬɨɤɨɜ ɦɟɠɞɭ ɧɢɦɢ ɩɪɟɞɭɫɦɚɬɪɢɜɚɸɬ

ɞɨɩɨɥɧɢɬɟɥɶɧɵɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜ ɤɚɠɞɨɦ ɷɦɢɬɬɟɪɟ, ɤɨɬɨɪɵɟ ɬɚɤɠɟ ɜɤɥɸɱɚɸɬɫɹ

ɜ

r

ɷ

. Ʉɥɸɱ Ʉɥ ɜ ɫɯɟɦɟ ɢɦɢɬɢɪɭɟɬ ɨɬɩɢɪɚɧɢɟ ɢ ɡɚɩɢɪɚɧɢɟ ɷɦɢɬɬɟɪɧɨɝɨ ɩɟɪɟɯɨɞɚ.

ȼɨ ɦɧɨɝɢɯ ɫɥɭɱɚɹɯ ɷɤɜɢɜɚɥɟɧɬɧɚɹ ɫɯɟɦɚ ɦɨɠɟɬ ɛɵɬɶ ɭɩɪɨɳɟɧɚ. ɇɚ ɱɚɫɬɨɬɚɯ ɞɨ

1...2 ȽȽɰ ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ ɺɦɤɨɫɬɹɦɢ

C

ɤɷ

,

C

ɤɛ

,

C

ɛɷ

. ɑɚɫɬɨ ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ ɢ

ɜɟɥɢɱɢɧɨɣ

r

ɤ

, ɚ

L

ɤ

ɜɤɥɸɱɚɸɬ ɜ ɫɯɟɦɭ ɰɟɩɢ ɫɨɝɥɚɫɨɜɚɧɢɹ.

ɇɚ ɞɨɫɬɚɬɨɱɧɨ ɜɵɫɨɤɢɯ ɱɚɫɬɨɬɚɯ, ɨɫɨɛɟɧɧɨ ɜ ɋȼɑ ɞɢɚɩɚɡɨɧɟ,

ɧɟɨɛɯɨɞɢɦɨ ɭɱɢɬɵɜɚɬɶ ɜɪɟɦɹ ɩɪɨɥɺɬɚ

τ

ɩɪ

ɧɨɫɢɬɟɥɟɣ ɡɚɪɹɞɚ ɱɟɪɟɡ ɛɚɡɭ

ɬɪɚɧɡɢɫɬɨɪɚ. ȼ ɞɚɥɶɧɟɣɲɟɦ, ɩɪɢ ɝɚɪɦɨɧɢɱɟɫɤɨɦ ɚɧɚɥɢɡɟ, ɷɬɨ ɦɨɠɧɨ ɫɞɟɥɚɬɶ

ɜɜɟɞɟɧɢɟɦ ɤɨɦɩɥɟɤɫɧɨɣ ɤɪɭɬɢɡɧɵ

S

ɉ

= S

ɉ

exp(–j

ωτ

ɩɪ

).

ɗ Ȼ Ʉ

p

r

ɛ

n C

ɤɩ

p C

ɤɚ

ɩɨɞɥɨɠɤɚ

Ɋɢɫ. 2.2. ɋɬɪɭɤɬɭɪɚ ɦɨɳɧɨɝɨ

ɛɢɩɨɥɹɪɧɨɝɨ ɬɪɚɧɡɢɫɬɨɪɚ

19

2.2.

Ƚɚɪɦɨɧɢɱɟɫɤɢɣ ɚɧɚɥɢɡ ɬɨɤɨɜ ɢ ɧɚɩɪɹɠɟɧɢɣ ɌɍɆ

ɇɚ ɜɵɫɨɤɢɯ ɱɚɫɬɨɬɚɯ ɜɯɨɞɧɨɣ ɬɨɤ ɦɨɳɧɵɯ ɬɪɚɧɡɢɫɬɨɪɨɜ ɨɤɚɡɵɜɚɟɬɫɹ

ɛɥɢɡɤɢɦ ɤ ɝɚɪɦɨɧɢɱɟɫɤɨɦɭ. ɗɬɨ ɩɪɨɢɫɯɨɞɢɬ ɢɡ-ɡɚ ɧɢɡɤɨɝɨ ɜɯɨɞɧɨɝɨ ɫɨɩ-

ɪɨɬɢɜɥɟɧɢɹ ɢ ɩɨɞɚɜɥɟɧɢɹ ɜɵɫɲɢɯ ɝɚɪɦɨɧɢɤ ɬɨɤɚ ɢɧɞɭɤɬɢɜɧɨɫɬɶɸ ɜɯɨɞɧɨɝɨ

ɷɥɟɤɬɪɨɞɚ ɢ ɢɧɞɭɤɬɢɜɧɨɫɬɹɦɢ ɰɟɩɟɣ ɫɜɹɡɢ ɫ ɩɪɟɞɵɞɭɳɢɦɢ ɤɚɫɤɚɞɚɦɢ. ɉɨɷɬɨɦɭ

ɛɭɞɟɦ ɫɱɢɬɚɬɶ, ɱɬɨ ɧɚ ɜɯɨɞɟ ɬɪɚɧɡɢɫɬɨɪɚ ɞɟɣɫɬɜɭɟɬ ɬɨɤ

i

ɛ

= I

ɛɨ

+ I

ɛ1

cos

τ

.

(2.2)

ɋɧɚɱɚɥɚ, ɞɥɹ ɭɩɪɨɳɟɧɢɹ ɚɧɚɥɢɡɚ, ɩɪɟɞɩɨɥɨɠɢɦ, ɱɬɨ

C

ɤɚ

= C

ɤɩ

= 0

. ȼ ɷɬɨɦ

ɫɥɭɱɚɟ ɜɯɨɞɧɨɣ ɬɨɤ ɪɚɜɟɧ ɬɨɤɭ, ɩɪɨɬɟɤɚɸɳɟɦɭ ɱɟɪɟɡ ɷɦɢɬɬɟɪɧɵɣ ɩɟɪɟɯɨɞ,

ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɤɨɬɨɪɨɝɨ ɪɚɡɥɢɱɧɨ ɜ ɨɬɤɪɵɬɨɦ ɢ ɡɚɤɪɵɬɨɦ ɫɨɫɬɨɹɧɢɹɯ.

ɍɱɢɬɵɜɚɹ, ɱɬɨ ɬɨɤ ɱɟɪɟɡ ɟɦɤɨɫɬɶ

C

ɪɚɜɟɧ

i C

du

dt

C

du

d t

C

du

d

c

c c c

= = =

ω

τ

,

ɝɞɟ

u

c

— ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɺɦɤɨɫɬɢ, ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɫɥɟɞɭɸɳɢɟ ɭɪɚɜɧɟɧɢɹ:

;,)()( Eu

r

Eu

dt

du

CCi

ɉ

ɉɉ

ɷɞ

ɛ

′

≥

′

−

++=

β

ωτ

(2.3, ɚ)

.,)( Eu

dt

du

Ci

ɉ

ɷ

ɛ

′

<=

ωτ

(2.3, ɛ)

Ⱥɧɚɥɢɬɢɱɟɫɤɨɟ ɪɟɲɟɧɢɟ ɫɢɫɬɟɦɵ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɵɯ ɭɪɚɜɧɟɧɢɣ (2.3)

ɞɨɜɨɥɶɧɨ ɫɥɨɠɧɨ. Ɇɵ ɜɨɫɩɨɥɶɡɭɟɦɫɹ ɝɨɬɨɜɵɦ ɪɟɲɟɧɢɟɦ ɢ ɥɢɲɶ ɤɚɱɟɫɬɜɟɧɧɨ

ɨɰɟɧɢɦ ɩɨɥɭɱɟɧɧɵɟ ɪɟɡɭɥɶɬɚɬɵ ɫ ɩɨɦɨɳɶɸ ɩɨɫɬɪɨɟɧɢɣ, ɩɨɤɚɡɚɧɧɵɯ ɧɚ ɪɢɫ.

2.3 .

i

ɛ

I

ɛ1

I

ɛɨ

τ

u

ɉ

u

ɫɷ

u

rc

E

′

τ

E

ɫɦ

τ

ɦ

Ɉɛɥɚɫɬɢ ɩɟɪɟɯɨɞ-

π⁄2 ɧɵɯ ɩɪɨɰɟɫɫɨɜ

Ɋɢɫ. 2.3. ȼɪɟɦɟɧɧɵɟ ɞɢɚɝɪɚɦɦɵ ɬɨɤɨɜ ɢ ɧɚɩɪɹɠɟɧɢɣ ɦɨɳɧɨɝɨ ɬɪɚɧɡɢɫɬɨɪɚ

20

ɉɪɢ ɡɚɤɪɵɬɨɦ ɫɨɫɬɨɹɧɢɢ ɩɟɪɟɯɨɞɚ ɛɚɡɚ-ɷɦɢɬɬɟɪ ɜɯɨɞɧɨɣ ɬɨɤ

i

ɛ

ɫɨɡɞɚɟɬ ɧɚ

C

ɷ

ɩɚɞɟɧɢɟ ɧɚɩɪɹɠɟɧɢɹ

u

ɫɷ

, ɨɬɫɬɚɸɳɟɟ ɩɨ ɮɚɡɟ ɧɚ π⁄2 ɨɬ

I

ɛ1

ɢ ɤɨɥɟɛɥɸɳɟɟɫɹ

ɜɨɤɪɭɝ ɧɚɩɪɹɠɟɧɢɹ

E

ɫɦ

(ɪɢɫ.2.3). ȼ ɨɬɤɪɵɬɨɦ ɫɨɫɬɨɹɧɢɢ ɬɨɤ

i

ɛ

ɫɨɡɞɚɟɬ ɩɚɞɟɧɢɟ

ɧɚɩɪɹɠɟɧɢɹ

u

rc

ɧɚ RC ɰɟɩɨɱɤɟ, ɫɨɫɬɨɹɳɟɣ ɢɡ ɩɚɪɚɥɥɟɥɶɧɨɝɨ ɫɨɟɞɢɧɟɧɢɹ

ɷɥɟɦɟɧɬɨɜ

r

β

,

C

ɞ

ɢ

C

ɷ

. ɇɚɩɪɹɠɟɧɢɟ

u

rc

ɨɬɫɬɚɟɬ ɩɨ ɮɚɡɟ ɨɬ

I

ɛ1

ɧɚ ɭɝɨɥ

τ

ɦ

<

π

⁄2,

ɤɨɥɟɛɥɟɬɫɹ ɨɤɨɥɨ

E

′

ɢ ɡɧɚɱɢɬɟɥɶɧɨ ɦɟɧɶɲɟ, ɱɟɦ

u

ɫɷ

ɜ ɡɚɤɪɵɬɨɦ ɫɨɫɬɨɹɧɢɢ

ɩɟɪɟɯɨɞɚ. ɇɚɩɪɹɠɟɧɢɟ ɧɚ ɩɟɪɟɯɨɞɟ







′

<

′

≥

=

.,

,,

Euu

u

ɉ

cɷ

rɫ

ɇɚɩɪɹɠɟɧɢɟ

u

rc

ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɪɟɲɟɧɢɸ ɭɪɚɜɧɟɧɢɹ (2.3, ɚ), ɚ

u

ɫɷ

— ɭɪɚɜɧɟɧɢɸ

(2.3, ɛ). Ʉɚɤ ɜɢɞɧɨ ɢɡ ɪɢɫ. 2.3 ɦɨɦɟɧɬɵ ɩɟɪɟɯɨɞɨɜ ɧɚɩɪɹɠɟɧɢɣ

u

ɫɷ

ɢ

u

rc

ɱɟɪɟɡ

E

′

ɧɟ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɞɪɭɝ ɞɪɭɝɭ. ɗɬɨ ɨɛɥɚɫɬɢ ɩɟɪɟɯɨɞɧɵɯ ɩɪɨɰɟɫɫɨɜ ɩɪɢ

ɨɬɩɢɪɚɧɢɢ ɢ ɡɚɩɢɪɚɧɢɢ ɬɪɚɧɡɢɫɬɨɪɚ. Ʉɚɱɟɫɬɜɟɧɧɨ ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɩɟɪɟɯɨɞɟ

u

ɉ

ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 2.3 ɭɬɨɥɳɟɧɧɨɣ ɥɢɧɢɟɣ. ȼɢɞɧɨ, ɱɬɨ ɮɨɪɦɚ ɧɚɩɪɹɠɟɧɢɹ ɧɚ

ɩɟɪɟɯɨɞɟ ɹɜɧɨ ɧɟɝɚɪɦɨɧɢɱɟɫɤɚɹ. ȼɵɯɨɞɧɨɣ ɬɨɤ ɬɪɚɧɡɢɫɬɨɪɚ, ɤɚɤ ɫɥɟɞɭɟɬ ɢɡ

(2.1), ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɢɦɩɭɥɶɫɵ ɬɨɤɚ, ɧɨ ɧɟɤɨɫɢɧɭɫɨɢɞɚɥɶɧɨɣ ɮɨɪɦɵ.

Ɉɞɧɚɤɨ ɪɟɚɥɶɧɭɸ ɮɨɪɦɭ ɢɦɩɭɥɶɫɨɜ ɞɥɹ ɭɩɪɨɳɟɧɢɹ ɚɧɚɥɢɡɚ ɦɨɠɧɨ ɡɚɦɟɧɢɬɶ

ɤɨɫɢɧɭɫɨɢɞɚɥɶɧɨɣ, ɱɬɨ ɧɟɡɧɚɱɢɬɟɥɶɧɨ ɫɧɢɡɢɬ ɬɨɱɧɨɫɬɶ ɪɚɫɱɟɬɨɜ. Ⱦɥɹ ɷɬɨɝɨ

ɧɚɩɪɹɠɟɧɢɟ ɧɚ ɩɟɪɟɯɨɞɟ ɩɪɟɞɫɬɚɜɢɦ ɜ ɫɥɟɞɭɸɳɟɣ ɮɨɪɦɟ:

( )

[ ]

Eu

Ĭ

T

Ir

Eu

ɉ

ɦ

ɛ

′

≥

−−

+

=

′

− coscos

1

2

1

ττ

ω

β

; (2.4, ɚ)

( ) ( )

[ ]

Eu

Ĭ

C

I

Eu

ɉ

ɦ

ɷ

ɛ

′

<

−−−=

′

− )cos(cos

1

πττ

ω

, (2.4, ɛ)

ɝɞɟ

Θ

— ɭɝɨɥ ɨɬɫɟɱɤɢ ɤɨɥɥɟɤɬɨɪɧɨɝɨ ɬɨɤɚ;

T

β

=

r

β

(

C

ɞ

+

C

ɷ

) ≅

r

β

C

ɞ

— ɩɨɫɬɨɹɧɧɚɹ ɜɪɟɦɟɧɢ, ɡɧɚɱɟɧɢɟ ɤɨɬɨɪɨɣ ɛɥɢɡɤɨ

ɤ ɫɪɟɞɧɟɦɭ ɜɪɟɦɟɧɢ ɠɢɡɧɢ ɧɟɨɫɧɨɜɧɵɯ ɧɨɫɢɬɟɥɟɣ ɜ ɛɚɡɟ. ɍɪɚɜɧɟɧɢɟ (2.4 ɚ)

ɬɚɤɠɟ ɨɩɪɟɞɟɥɹɟɬ ɮɨɪɦɭ ɤɨɥɥɟɤɬɨɪɧɨɝɨ ɬɨɤɚ.

ɉɨ ɯɚɪɚɤɬɟɪɭ ɩɪɨɯɨɞɹɳɢɯ ɜ ɬɪɚɧɡɢɫɬɨɪɟ ɩɪɨɰɟɫɫɨɜ ɜɟɫɶ ɪɚɞɢɨɱɚɫɬɨɬɧɵɣ

ɞɢɚɩɚɡɨɧ ɦɨɠɧɨ ɪɚɡɞɟɥɢɬɶ ɧɚ ɬɪɢ ɱɚɫɬɢ.

1. ɇɢɡɤɨɱɚɫɬɨɬɧɵɣ ɞɢɚɩɚɡɨɧ, ɜ ɤɨɬɨɪɨɦ

ω

< 1/3T

β

, ɧɚ ɩɪɚɤɬɢɤɟ ɧɟ

ɩɪɢɦɟɧɹɟɬɫɹ ɢɡ-ɡɚ ɧɟɜɨɡɦɨɠɧɨɫɬɢ ɪɟɚɥɢɡɚɰɢɢ ɪɟɠɢɦɚ ɜɨɡɛɭɠɞɟɧɢɹ ɝɚɪ-

ɦɨɧɢɱɟɫɤɢɦ ɬɨɤɨɦ.

2. ɋɪɟɞɧɟɱɚɫɬɨɬɧɵɣ ɞɢɚɩɚɡɨɧ, ɜ ɤɨɬɨɪɨɦ

1

3

T T

β β

ω

< < .

ȼ ɷɬɨɦ ɞɢɚɩɚɡɨɧɟ ɬɨɤ ɤɨɥɥɟɤɬɨɪɚ ɛɭɞɟɬ ɢɦɟɬɶ ɮɨɪɦɭ, ɛɥɢɡɤɭɸ ɤ ɤɨɫɢɧɭ-

ɫɨɢɞɚɥɶɧɵɦ ɢɦɩɭɥɶɫɚɦ:

Воробьев М.С. Устройства генерирования радиосигналов

Подождите немного. Документ загружается.