Вольдек А.И. Электрические машины

Подождите немного. Документ загружается.

Механическая характеристика двигателя представляет собой

зависимость скорости вращения п от развиваемого момента на

валу М

при U

= const и = const:

n = f(MJ

или, наоборот,

M, = f(n).

Так как при нагрузке момент М

мал по сравнению с УИ и М

то можно положить М

« 0 или включить М

в величину статиче-

ского тормозящего момента УИ

СТ

, который развивается рабочей

машиной или механизмом, приводимым во вращение асинхронным

двигателем. Поэтому ниже в качестве механической характеристики

двигателя будем рассматривать зависимость между п (или s) и

электромагнитным моментом М:

n = f(M); M = f(n). (25-30)

Изображенные на рис. 25-1 и 25-3 кривые момента М при ука-

занных условиях и представляют собой механические характери-

стики асинхронного двигателя с постоянными параметрами.

Очевидно, что вид механических характеристик существенно

зависит от величины вторичного активного сопротивления.

Процесс пуска и установившийся режим работы асинхронного

двигателя. Рассмотрим процесс пуска асинхронного двигателя с ко-

роткозамкнутой вторичной обмоткой при его включении на полное

напряжение сети. Так производится пуск подавляющего большин-

ства находящихся в эксплуатации асинхронных двигателей. При

рассмотрении процесса пуска не будем принимать во внимание

электромагнитные переходные процессы, связанные с тем, что

при включении любой электрической цепи электромагнитного ме-

ханизма под напряжение и при изменении режима его работы токи

достигают практически установившихся значений не сразу, а после

истечения некоторого времени, величина которого пропорциональна

электромагнитной постоянной времени Т, зависящей от индуктив-

ности и активного сопротивления цепи. Обычно при пуске асин-

хронного двигателя время его разбега до нормальной скорости

значительно больше длительности электромагнитных переходных

процессов, и поэтому влияние этих процессов на процесс пуска

невелико. Следовательно, процесс пуска можно рассматривать на

основе полученных выше зависимостей для вращающего момента

и токов в условиях работы двигателя при установившемся режиме

с заданным скольжением.

На рис. 25-4 показана механическая характеристика М = f(n)

асинхронного двигателя и механическая характеристика Л4

СТ

= f (п)

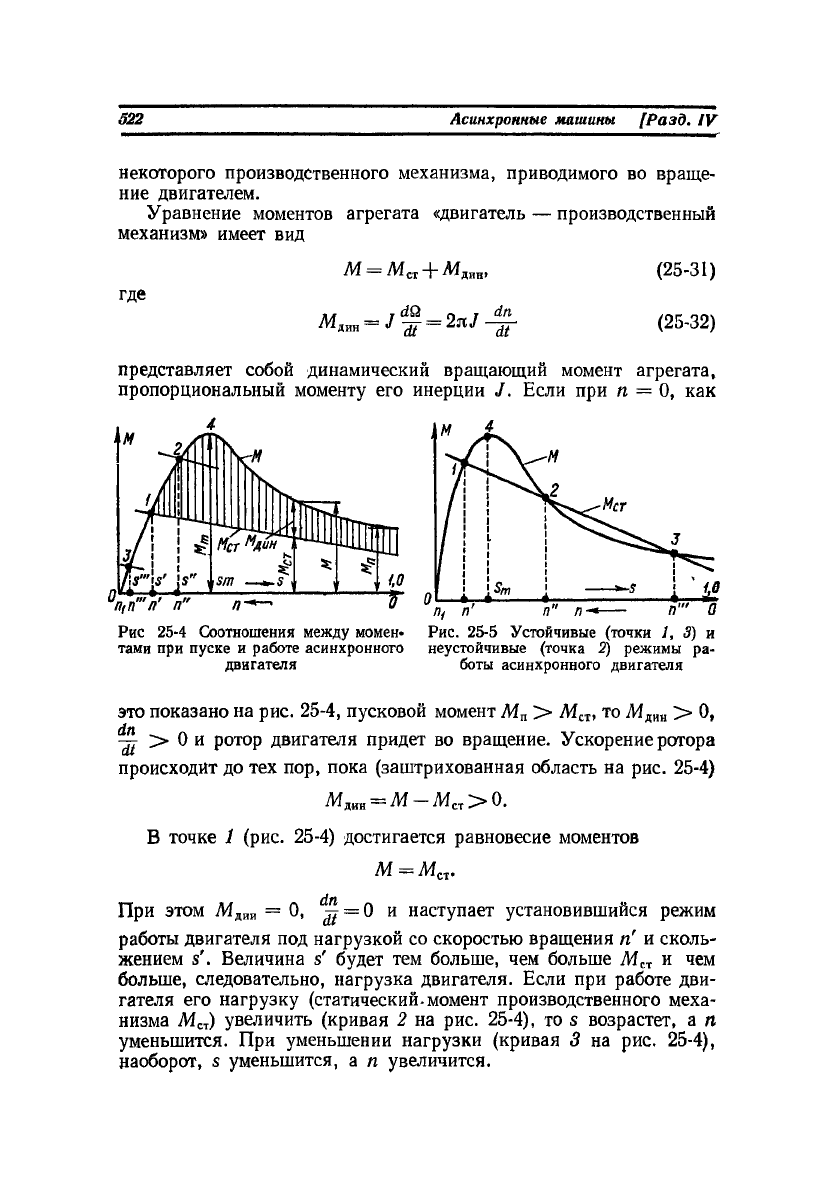
некоторого производственного механизма, приводимого во враще-

ние двигателем.

Уравнение моментов агрегата «двигатель — производственный

механизм» имеет вид

М = М

ст

+ М

тю

(25-31)

где

= = (25-32)

представляет собой динамический вращающий момент агрегата.

тами при пуске и работе асинхронного неустойчивые (точка 2) режимы ра-

двигателя боты асинхронного двигателя

это показано на рис. 25-4, пусковой момент М

> М

ст

, то М

лт

>• О,

^ > 0 и ротор двигателя придет во вращение. Ускорение ротора

происходит до тех пор, пока (заштрихованная область на рис. 25-4)

тя

= М-М

сг

>0.

В точке 1 (рис. 25-4) достигается равновесие моментов

М = М

СТ

При этом М

дии

= 0, ^ = 0 и наступает установившийся режим

работы двигателя под нагрузкой со скоростью вращения п' и сколь-

жением s'. Величина s' будет тем больше, чем больше М

СТ

и чем

больше, следовательно, нагрузка двигателя. Если при работе дви-

гателя его нагрузку (статический, момент производственного меха-

низма М

ст

) увеличить (кривая 2 на рис. 25-4), то s возрастет, а п

уменьшится. При уменьшении нагрузки (кривая 3 на рис. 25-4),

наоборот, s уменьшится, а п увеличится.

Переход двигателя к новому установившемуся режиму работы

при изменении нагрузки физически происходит следующим обра-

зом. Если Мп возрастет, то будет М < Af

, М

лт

< 0, ^ < 0 и

движение ротора двигателя станет замедляться. При этом сколь-

жение возрастает, в соответствии с чем увеличиваются также э. д. с.

И ТОК

вторичной цепи. В результате электромагнитный момент

М увеличивается и уменьшение п (увеличение s) происходит до тех

пор, пока снова не наступит равенство моментов М = М

СТ

. При

уменьшении нагрузки процесс протекает в обратном напра-

влении.

Как видно из рис. 25-4, при круто поднимающейся начальной

(левой) части кривой момента М = / (s) асинхронный двигатель

обладает жесткой механической характеристикой, т. е. при изме-

нении нагрузки скорость вращения двигатедя изменяется мало.

Все нормальные асинхронные двигатели строятся с жесткой

механической характеристикой, когда г'

и s

относительно малы.

При этом s и, следовательно, р

вда

[см. равенство (24-72)] при

работе также малы и двигатель имеет высокий к. п. д.

Условия устойчивой работы. В общем случае, как показано на

рис. 25-5, характеристики двигателя М = / (п) и производствен-

ного механизма М

ст

= f (п) могут иметь несколько точек пере-

сечения.

В точках 1 а 3

dM dM

dn dn >

(25-33)

и, согласно § 10-3, в этих точках работа устойчива, а в точке 2

(25-34)

и работа неустойчива.

При пуске из неподвижного состояния двигатель достигает

устойчивой скорости вращения в точке и'" (рис. 25-5) и дальнейщее

увеличение п невозможно, так как влево от этой точки М„ > М.

Если бы двигатель работал в режиме; соответствующем точке 2

(рис. 25-5), то при малейших нарушениях режима и изменении п

соотношения между М и М

ст

стали бы такими, что двигатель пере-

шел бы на работу в режиме, соответствующем одной из устойчивых

точек 1 или 3. Режим работы в точке 3 на практике неприемлем,

так как характеризуется малой скоростью вращения, плохим к. п. д.

и наличием больших токов в обмотках, вследствие чего двигатель

быстро перегревается и выходит из строя. Поэтому нормальной

устойчивой областью работы двигателя считается участок механи-

ческой характеристики влево от точки 4 (рис. 25-4), когда 0 < s <

Перегрузочная способность асинхронного двигателя. При работе

двигателя на нормальном устойчивом участке механической харак-

теристики (влево от точек 4 на рис. 25-4 и 25-5) его нагрузку, опре-

деляемую статическим моментом М

ст

рабочего механизма или ма-

шины, можно постепенно поднять до величины УИ

СТ

= М

(точки

4 на рис. 25-4 и 25-5), причем устойчивая работа сохраняется вплоть

до этой точки. При дальнейшем увеличении нагрузки, когда М

СТ

>•

>• М

, двигатель будет быстро затормаживаться и либо остановится,

либо при характеристиках вида рис. 25-5 перейдет в устойчивый

режим работы при малой скорости вращения. В обоих случаях, есди

двигатель не будет отключен, возникает опасный в отношении на-

грева режим.

Таким образом, в принципе работа асинхронного двигателя

возможна при 0 < М < М

. Однако продолжительная работа

при М М

в отношении нагрева также недопустима.

Кроме того, при работе двигателя необходимо иметь некоторый

запас по моменту, так как возможны кратковременные перегрузки

случайного характера, а также кратковременные или длительные

понижения напряжения сети.

Так как М

U\, то при уменьшении и

например, на 15%

максимальный момент двигателя снизится до 0,85

= 0,72 или 72%

от своего первоначального значения.

В связи с изложенным всегда должно быть М

> М

Отношение максимального момента при номинальном напря-

жении к номинальному

= М

/М

(25-35)

определяет перегрузочную способность двигателя и называется

кратностью максимального момента. Со-

гласно ГОСТ 186—52 и ГОСТ 9362—60, для двигателей разных

мощностей и скоростей вращения требуется, чтобы k

>• 1,7 -з-

2,2. Меньший предел относится к двигателям со скоростью

вращения п ^ 750 об/мин.

Кратности начального пускового момента и пускового тока.

Часто асинхронные двигатели можно пускать в ход на холостом

ходу или с малой нагрузкой на валу и нагружать их до номиналь-

ной или иной мощности после достижения нормальной скорости

вращения. В других случаях рабочие механизмы и машины (напри-

мер, вентиляторы) имеют механическую характеристику Л1

СТ

= f (/г) такого вида, что при п = 0 статический момент М

ст

мал

и постепенно повышается с увеличением п. При этом не требуется,

чтобы двигатель развивал большой пусковой момент. Однако иногда

двигатели необходимо пускать в ход под значительной нагрузкой

(например, крановые механизмы, подъемники, различные мельницы

и т. д.), и в этих случаях требуется, чтобы двигатели имели боль-

шие пусковые моменты.

Асинхронные двигатели с фазным ротором можно пускать в ход

с помощью реостата, включаемого на время пуска во вторичную

цепь двигателя. Как следует из § 25-1 (см. рис. 25-3), при этом пу-

сковой момент двигателя увеличивается, а пусковой ток умень-

шается. Поэтому стандарты не регламентируют величин пусковых

моментов и токов асинхронных двигателей с фазным ротором. В то

же время выпускаемые электромашиностроительными заводами

серийные асинхронные двигатели с короткозамкнутым ротором

должны удовлетворять разнообразным условиям пуска производ-

ственных механизмов и их пусковые моменты должны быть доста-

точно велики.

Согласно ГОСТ 186—52 и ГОСТ 9362—60, короткозамкнутые

асинхронные двигатели должны иметь при пуске под номиналь-

ным напряжением кратность начального пускового момента М

(s = 1, п = 0)

= M

(25-36)

не менее 0,7—1,8. Меньшие значения относятся к двигателям

большей мощности. Кратность пускового тока

=^ (25-37)

для двигателей с короткозамкнутым ротором разных мощностей

и разных скоростей вращения при этом должна быть не больше

5,5—7,0.

Пригодность асинхронных двигателей с короткозамкнутым рото-

ром и с постоянными параметрами в качестве двигателей общего

назначения. Как уже указывалось, для получения хорошего к. п. д.

асинхронные двигатели должны работать при номинальной нагрузке

с малым скольжением (s = 0,02 -г- 0,05) и иметь, таким образом,

жесткую механическую характеристику (s

= 0,06 н- 0,15). Это

требование для двигателей с короткозамкнутым ротором и с по-

стоянными параметрами вступает в противоречие с требованием

о достаточной величине пускового момента двигателя. Действи-

тельно, как видно из кривой 1 рис. 25-3, пусковой момент при этих

условиях получается недостаточно большим. Это же можно уста-

новить по соотношению (25-25), если переписать его один раз для

режима пуска (s = 1, М — М

), другой раз — для номинального

режима (s = s

, М = М

) и разделить получаемые соотношения

друг на друга. При этом будем иметь

/7I

"Ь

Мн ~ l/s

+ s

Например, при s

= 0,03 и s

= 0,10

_ 0,03/0,10 + 0,10/0,03 _ 3^63

„„

~ 1/0,10 + 0,10 10,1

Таким образом, двигатели с постоянными параметрами разви-

вают недостаточный пусковой момент. В связи с этим двигатели

общего назначения с короткозамкнутым ротором строятся исключи-

тельно как двигатели с переменными параметрами. При этом для

увеличения в период пуска и для увеличения тем самым М„

используется явление поверхностного эффекта или вытеснения тока

в обмотке ротора (см. гл. 27).

§ 25-3. Электромагнитные моменты и силы от высших гармоник

магнитного поля

Выше рассматривался электромагнитный момент, создаваемый основной

гармоникой поля. Наряду с основной гармоникой существуют также высшие и

"низшие гармоники ncwyi, вызванные наличием гармоник н с. обмоток и зубчатым

строением статора и ротора. Эти гармоники поля также создают вращающие

моменты, которые можно подразделить на асинхронные и синхронные.

Вращающие моменты создаются тангенциальными электромагнитными си-

лами. Кроме этих сил, действуют также радиальные электромагнитные силы,

которые вызывают вибрацию и шум машины.

Указанные моменты и силы проявляются наиболее сильно при скольжениях,

близких к единице, т. е. при пуске и торможении двигателя. Причина этого

заключается, во-первых, в том, что при s = 1 токи велики. Во-вторых, высшие

гармоники поля вращаются медленно и синхронная скорость вращения ротора

для них мала, а моменты достигают максимальных значений вблизи их синхрон-

ной скорости.

Остановимся кратко на перечисленных явлениях.

Асинхронные моменты. Рассмотрим, например, седьмую гармонику поля

статора^ = 7), которая вращается в том же направлении, что и основная, со

скоростью п

— у- п

. При вращении этой гармоники относительно ротора в об-

мотке ротора индуктируются э. д. с. и токи и создается вращающий момент М-,,

так же как и в результате действия основной гармоники поля. В момент пуска,

при 5=1, момент М

> 0 и действует согласно с моментом основной гармоники

Mi (рис. 26-6). Когда ротор придет во вращение в сторону вращения основной

гармоники (s < 1), относительная скорость поля седьмой гармоники и ротора

начнет уменьшаться. При скорости ротора п = щ.П или s = 6/7 седьмая гармо-

ника поля будет относительно него неподвижна и М

= 0 При дальнейшем уве-

личении п ротор вращается быстрее седьмой гармоники поля, по отношению

к нему возникает генераторный режим работы и /И, < 0 (рис. 25-6).

Пятая гармоника поля вращается в обратном направлении, и синхронное

вращение ротора относительно нее наступает в тормозном режиме — при п =

= — rti/5 или s = 6/5. Кривая момента этой гармоники М

также изображена

на рис. 25-6.

Подобные же кривые моментов создаются другими гармониками поля, поэтому

кривая результирующего момента

Al = Af

+ Al

-|-Af

+ ...

искажается (рис. 25-6) и в ней возникают провалы. При большой величине этих

провалов и достаточно большом статическом моменте УИ

СТ

на валу может насту-

пить устойчивый режим работы при малой скорости вращения в процессе пуска

двигателя (точка а на рис. 25-6) или при его торможении (точка б на рис. 25-6),

в результате чего двигатель не достигает нормальной скорости вращения. При

пуске опасным является действие прямых гармоник поля, а при торможении —

обратных. Ввиду изложенного моменты от высших гармоник поля называются

также паразитными.

Рис. 25-6. Искажение кривой момента асин- Рис. 25-7. Токи в беличьей

хроиными моментами от высших гармоник клетке, индуктируемые выс-

поля шими гармониками поля

Согласно ГОСТ 186—52, отношение минимального момента в процессе пуска

к номинальному для двигателей мощностью 0,6—100 квт не должно быть мень-

ше 0,8.

При фазной обмотке ротора искажение кривой моментов незначительно. Это,

с одной стороны, объясняется тем, что ввиду малых значений обмоточных коэф-

фициентов такой обмотки для высших гармоник поля индуктируемые гармоники

э. д. с. невелики. С другой стороны, индуктивное сопротивление рассеяния такой

обмотки для токов от высших гармоник поля велико.

Это

вызвано тем, что токи,

индуктируемые v-й гармоникой поля статора в обмотке ротора, создают, кро-

ме v-fi же гармоники, также гармонику v = 1 поля ротора, которая значи-

тельно больше гармоник и в данном случае по отношению к v-й индуктирую-

щей гармонике составляет поле рассеяния.

Отметим, что высшие гармоники поля самого ротора в свою очередь индук-

тируют токи в обмотке статора и поэтому также создают паразитные моменты

рассмотренного выше характера. Поскольку, однако, обмотка статора всегда

является фазной, то эти моменты незначительны.

Реальную опасность моменты высших гармоник вызывают в случае коротко-

замкнутой обмотки ротора, так как при этом для токов от высших гармоник

поля могут создаваться короткие цепи, состоящие из соседних илр близлежащих

стержней и участков колец и обладающие весьма малым сопротивлением (рис. 25-7).

Возможность образования таких цепей тем больше, чем больше число пазов

ротора

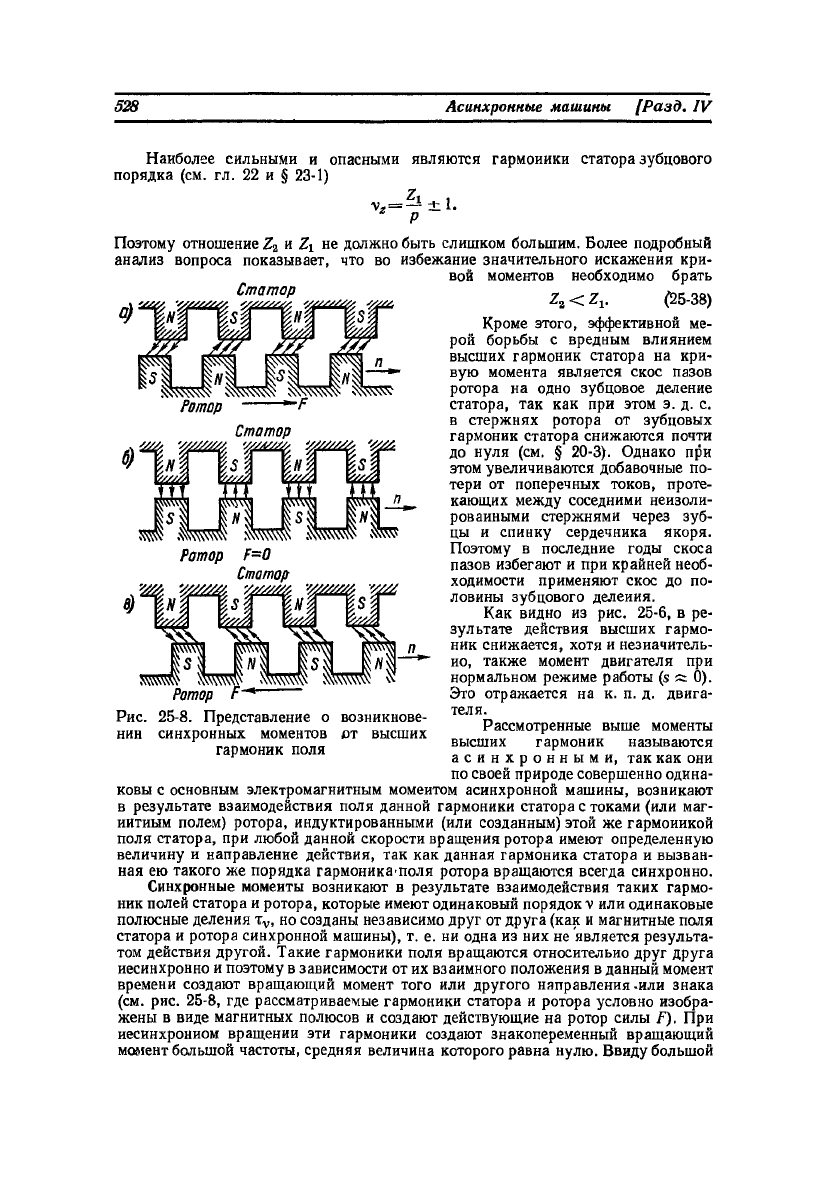
Ротор F=0

Статор

Наиболее сильными и опасными являются гармоники статора зубцового

порядка (см. гл. 22 и § 23-1)

i 1

Поэтому отношение Z

и Z\ не должно быть слишком большим. Более подробный

анализ вопроса показывает, что во избежание значительного искажения кри-

вой моментов необходимо брать

Стат0Р

. (25-38)

Кроме этого, эффективной ме-

рой борьбы с вредным влиянием

высших гармоник статора на кри-

вую момента является скос пазов

ротора на одно зубцовое деление

статора, так как при этом э. д. с.

в стержнях ротора от зубцовых

гармоник статора снижаются почти

до нуля (см. § 20-3). Однако при

этом увеличиваются добавочные по-

тери от поперечных токов, проте-

кающих между соседними неизоли-

рованными стержнями через зуб-

цы и спинку сердечника якоря.

Поэтому в последние годы скоса

пазов избегают и при крайней необ-

ходимости применяют скос до по-

ловины зубцового деления.

Как видно из рис. 25-6, в ре-

зультате действия высших гармо-

ник снижается, хотя и незначитель-

но, также момент двигателя при

нормальном режиме работы (s я: 0).

Это отражается на к. п. д. двига-

теля.

Рассмотренные выше моменты

высших гармоник называются

асинхронными, так как они

по своей природе совершенно одина-

ковы с основным электромагнитным моментом асинхронной машины, возникают

в результате взаимодействия поля данной гармоники статора с токами (или маг-

нитным полем) ротора, индуктированными (или созданным) этой же гармоникой

поля статора, при любой данной скорости вращения ротора имеют определенную

величину и направление действия, так как данная гармоника статора и вызван-

ная ею такого же порядка гармоника>поля ротора вращаются всегда синхронно.

Синхронные моменты возникают в результате взаимодействия таких гармо-

ник полей статора и ротора, которые имеют одинаковый порядок v или одинаковые

полюсные деления T

, но созданы независимо друг от друга (как и магнитные поля

статора и ротора синхронной машины), т. е. ни одна из них не является результа-

том действия другой. Такие гармоники поля вращаются относительно друг друга

несинхронно и поэтому в зависимости от их взаимного положения в данный момент

времени создают вращающий момент того или другого направления-или знака

(см. рис. 25-8, где рассматриваемые гармоники статора и ротора условно изобра-

жены в виде магнитных полюсов и создают действующие на ротор силы F). При

несинхронном вращении эти гармоники создают знакопеременный вращающий

момент большой частоты, средняя величина которого равна нулю. Ввиду большой

Ротор

Рис. 25-8. Представление о возникнове-

нии синхронных моментов от высших

гармоник поля

механической инерции ротора этот момент на движение ротора влияния не ока-

зывает.

Однако при некоторой, вполне определенной скорости ротора п = n

такие

гармоники могут вращаться синхронно, и при этом в зависимости от их взаимного

положения создается положительный или отрицательный момент M

той или

иной величины в пределах — М

стмакс

гС M

гС + M

CVMaK(

.. Величина этого

момента изобразится на кривой М = f (s) в виде определенной точки на вертикаль-

ном отрезке прямой аб (рис. 25-9). Из-за действия этого момента при пуске дви-

гатель может «застрять» на скорости вращения n

и не «дойти» до нормальной

скорости. Но в отличие от асинхронных моментов в данном случае имеется большая

вероятность того, что ротор вследствие своей инерции перейдет через зону

опасного действия синхронного момента. Поэтому, если синхронные моменты

возникают при скорости п ф 0, то они менее опасны, чем асинхронные моменты.

Рассмотрим пример, когда синхронный момент создается гармониками зуб-

цового порядка, которые являются наибо-

лее сильными.

Пусть обмотка статора имеет т

= 3,

2р = 4, Zi = 24, а короткозамкнутый ротор

имеет Z

= 28. Тогда гармоники первого зуб-

цового порядка, создаваемые током статора

и током основной частоты = sf

ротора,

будут равны: прямая гармоника статора

= Z

/p+1 = 24/2 +

= 13

и обратная

v^j = Zj/p—1 = 24/2—

= 11;

прямая гармоника ротора

JP +

и обратная

v^ = Z

/p-1 = 28/2-1 = 13.

Таким образом, одинаковый порядок имеют прямая гармоника статора и

обратная гармоника ротора = v"

= 13. Первая из них вращается относи-

тельно статора со скоростью nj

13,

а вторая — относительно ротора со скоростью

snj _ п^

— п

~"13 13~

и относительно статора со скоростью

Скорости этих гармоник относительно статора одинаковы, когда

"г -„

13 13 '

откуда п = nJT, т. е. синхронный момент возникает в двигательном режиме во

время пуска при скорости, равной одной седьмой синхронной скорости.

В рассматриваемом случае Z

— Z

= 4 = 2р. Нетрудно видеть, что син-

хронные моменты возникают всегда в результате взаимодействия зубцовых гар-

моник первого порядка при вращении ротора при

-Z

=±2p,

Рис. 25-9. Искажение кривой

моментов синхронным моментом

от высших гармоник поля

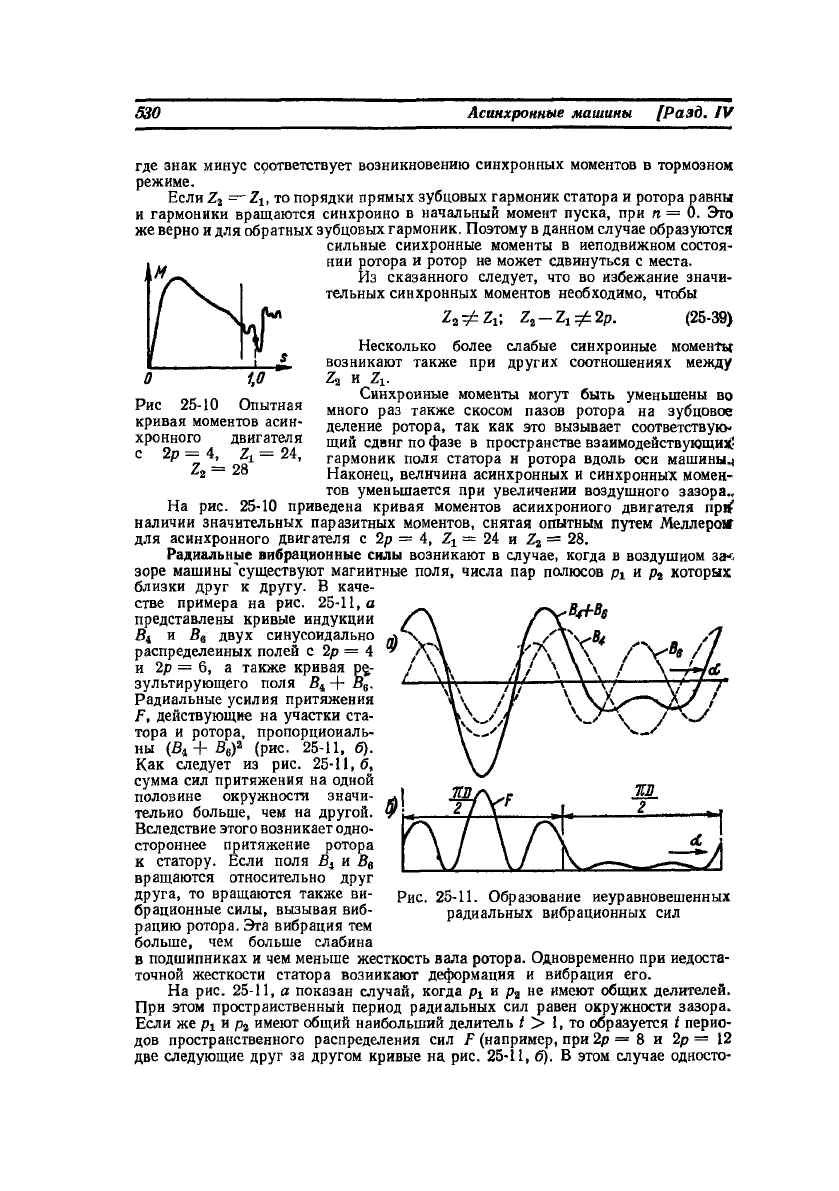
где знак минус соответствует возникновению синхронных моментов в тормозном

режиме.

Если

Z-i

— Z

то порядки прямых зубцовых гармоник статора и ротора равны

и гармоники вращаются синхронно в начальный момент пуска, при п = 0. Это

же верно и для обратных зубцовых гармоник. Поэтому в данном случае образуются

сильные синхронные моменты в неподвижном состоя-

нии ротора и ротор не может сдвинуться с места.

Из сказанного следует, что во избежание значи-

тельных синхронных моментов необходимо, чтобы

^Zi, Z

-Z

z^2p. (25-39)

0 1,0

Рис 25-10 Опытная

кривая моментов асин-

хронного двигателя

с 2р = 4, Z

= 24,

= 28

Несколько более слабые синхронные моменты

возникают также при других соотношениях между

и Z

Синхронные моменты могут быть уменьшены во

много раз также скосом пазов ротора на зубцовое

деление ротора, так как это вызывает соответствую-

щий сдвнгпофазе в пространстве взаимодействующих!

гармоник поля статора и ротора вдоль оси машины.!

Наконец, величина асинхронных и синхронных момен-

тов уменьшается при увеличении воздушного зазора.»

На рис. 25-10 приведена кривая моментов асинхронного двигателя nprf

наличии значительных паразитных моментов, снятая опытным путем Меллеро*

для асинхронного двигателя с 2р = 4, Z

= 24 и Z

= 28.

Радиальные вибрационные силы возникают в случае, когда в воздушном за*

зоре машины "существуют магнитные поля, числа пар полюсов р

и р

которых

близки друг к другу. В каче-

стве примера на рис. 25-11, с

представлены кривые индукции

Bft-Bg

и В

двух синусоидально

распределенных полей с 2р = 4

и 2р = 6, а также кривая ре-

зультирующего поля В

+ В

Радиальные усилия притяжения

F, действующие на участки ста-

тора и ротора, пропорциональ-

ны (fl

+ В

)

(рис. 25-11, б).

Как следует из рис. 25-11,6,

сумма сил притяжения на одной

половине окружности значи-

тельно больше, чем на другой.

Вследствие этого возникает одно-

стороннее притяжение ротора

к статору. Если поля B

и В

вращаются относительно друг

друга, то вращаются также ви-

брационные силы, вызывая виб-

рацию ротора. Эта вибрация тем

больше, чем больше слабина

в подшипниках и чем меньше жесткость вала ротора. Одновременно при недоста-

точной жесткости статора возникают деформация и вибрация его.

На рис. 25-11, а показан случай, когда Pi и р

не имеют общих делителей.

При этом пространственный период радиальных сил равен окружности зазора.

Если же pi и р

имеют общий наибольший делитель t > 1, то образуется t перио-

дов пространственного распределения сил F (например, при 2р = 8 и 2р = 12

две следующие друг за другом кривые на рис. 25-11, б). В этом случае односто-

Рис. 25-11. Образование неуравновешенных

радиальных вибрационных сил