Вольдек А.И. Электрические машины

Подождите немного. Документ загружается.

Подставив эти значения E

и Е

в (20-13), получим формулу для

вычисления k

(20-15)

Очевидно, что при q = 1 имеем k

= 1, а при q > 1 будет k

< 1.

Если в пределах угла фазной зоны а величину q увеличить,

переходя ко все более мелким пазам, то в идеализированном пре-

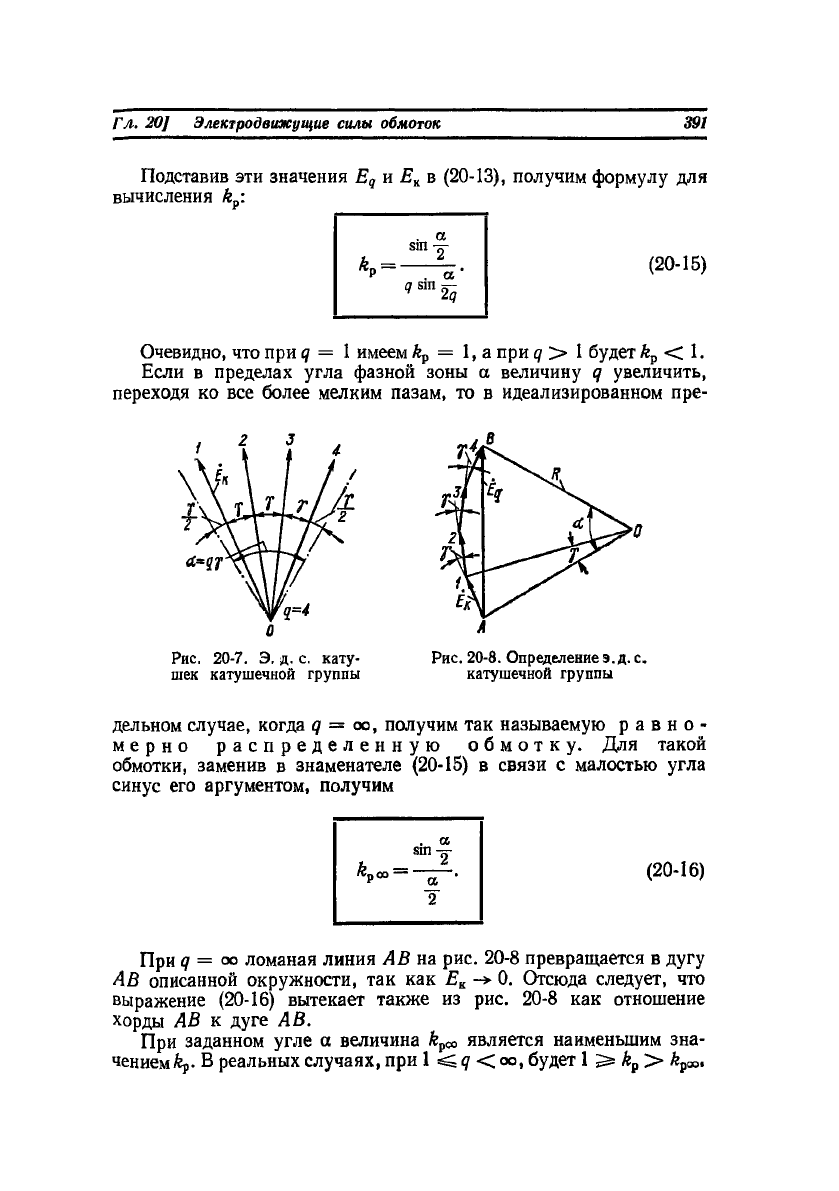
Рис. 20-7. Э. д. с. кату-

шек катушечной группы

Рис. 20-8. Определение э. д. с.

катушечной группы

дельном случае, когда q = оо, получим так называемую равно-

мерно распределенную обмотку. Для такой

обмотки, заменив в знаменателе (20-15) в связи с малостью угла

синус его аргументом, получим

(20-16)

При q = оо ломаная линия А В на рис. 20-8 превращается в дугу

АВ описанной окружности, так как Е

-> 0. Отсюда следует, что

выражение (20-16) вытекает также из рис. 20-8 как отношение

хорды АВ к дуге АВ.

При заданном угле а величина £

рСО

является наименьшим зна-

чением Ар. В реальных случаях, при

< оо, будет

> fe

p00

На основании выражений (20-10) и (20-14)

= п V2

fqw

<t>,

(20-17)

где величина

(20-18)

учитывает укорочение шага и распределение обмотки и называется

обмоточным коэффициентом. Величину k

также

можно было бы ввести в качестве сомножителя в выражение для

. Однако обычно этого не делают, так как скос влияет на вели-

чину э. д. с. лишь в том случае, когда пазы и проводники обмотки

скошены относительно магнитного поля. Иногда же магнитное

поле ориентировано вдоль скошенных пазов, и в этом случае скос

на величину э. д. с. не влияет.

Э. д. с. фазы обмотки. В многополюсной машине каждая фаза

обмотки содержит ряд катушечных групп, лежащих под разными

полюсами (см. гл. 21). В наиболее распространенном случае все

группы содержат одинаковое количество катушек q, занимают

поэтому одинаковые углы а и сдвинуты относительно друг друга

на целое число полюсных делений. В этом случае э. д. с. всех кату-

шечных групп равны по величине и сдвинуты по фазе на 360° (при

сдвиге групп на четное число т) или на 180 (при сдвиге

нй"

нечетное

число т). Такие катушечные группы можно соединить последова-

тельно таким образом, что э. д. с. групп будут складываться ариф-

метически. Возможно также их параллельное и смешанное соеди-

нение так, что э. д. с. всех параллельных ветвей будут одинаковы

по величине и совпадут по фазе. Если в каждой ветви соединено по-

следовательно п катушечных групп, то действующее значение

э. д. с. каждой ветви и фазы обмотки в целом будет

E = tlEq

или на основании выражения (20-17)

Е = п

У%

fwk

k,0 = 4,44/т>£

о6

Ф. (20-19)

Здесь

nqw

(20-20)

представляет собой число последовательно соединенных витков

каждой параллельной ветви и называется числом витков

фазы.

Если m-фазная обмотка заполняет все Z пазов и имеет а парал-

лельных ветвей, то

(20-21)

/ *

180°

\ 180' А

«.=60° А

где s„ — число эффективных проводников в пазу. Эффективный про-

водник может состоять из одного или некоторого числа параллель-

ных проводников.

В более сложных случаях, когда

отдельные катушечные группы состоят

из различного количества катушек,

также применима формула (20-19),

если рассчитывать соответствующим

образом коэффициент распределения

обмотки 6

(см. § 21-2).

Выражение (20-19) отличается от

выражения для э. д. с. обмотки транс-

форматора только наличием множите-

ля k

, который при b

Ф 0, р Ф 1 и

q > 1 меньше единицы. Это объяс-

няется тем, что при 0 и р ^ 1

поток полюса сцепляется с катушкой

неполностью и при q> 1 в каждый

момент времени потокосцепление раз-

личных катушек различно." Величина

называется также эффектив-

ным числом витков обмотки.

Так как

„ Е

<оУ

60°

60' I

60') 60'\ 60'\60'

•120'

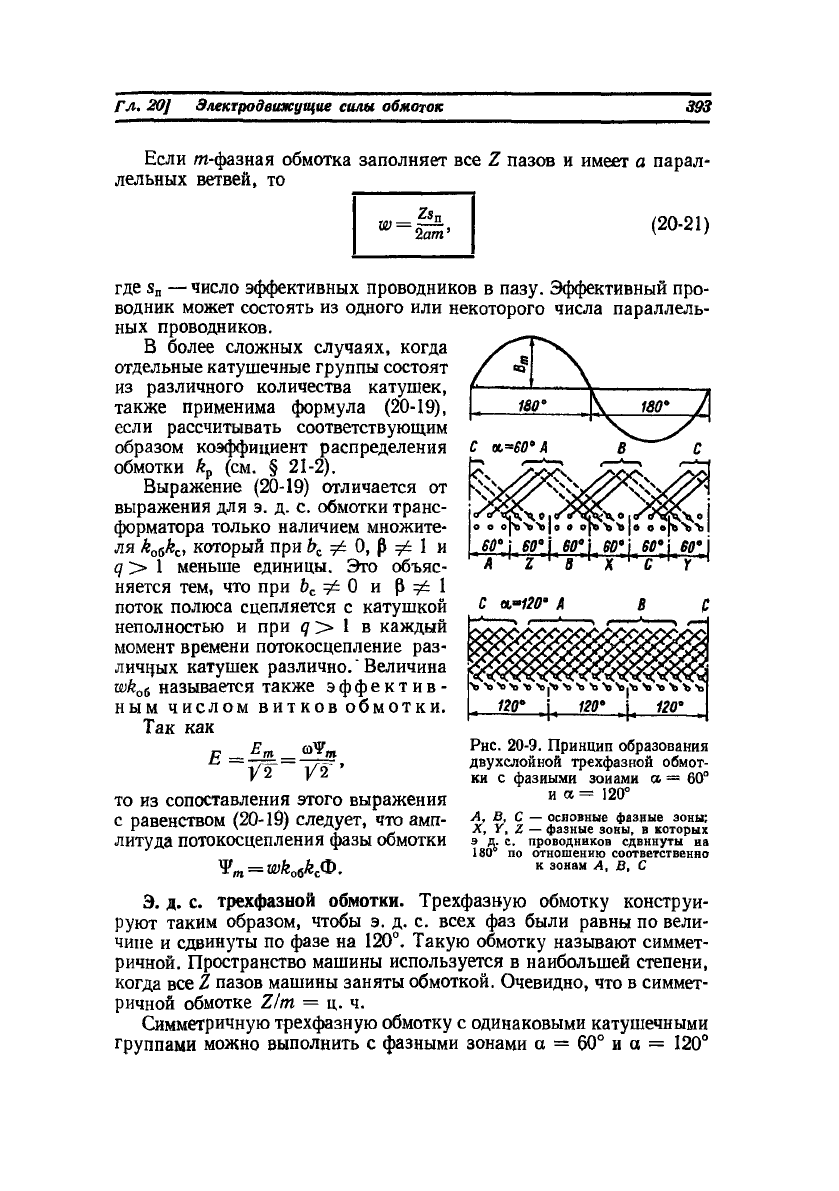
УЧ /2

Рнс. 20-9. Принцип образования

двухслойной трехфазной обмот-

ки с фазными зонами а = 60°

и а = 120°

А. В, С — основные фазные зоны;

X, Y. Z — фазные зоны, в которых

д. с. проводников сдвинуты иа

ап

по отношению соответственно

к зонам А, В, С

180

то из сопоставления этого выражения

с равенством (20-19) следует, что амп-

литуда потокосцепления фазы обмотки

= wk

k&.

Э. д. с. трехфазной обмотки. Трехфазную обмотку конструи-

руют таким образом, чтобы э. д. с. всех фаз были равны по вели-

чине и сдвинуты по фазе на 120°. Такую обмотку называют симмет-

ричной. Пространство машины используется в наибольшей степени,

когда все Z пазов машины заняты обмоткой. Очевидно, что в симмет-

ричной обмотке Zltn = ц. ч.

Симметричную трехфазную обмотку с одинаковыми катушечными

группами можно выполнить с фазными зонами а = 60° и а = 120°

(рис. 20-9). Очевидно, что обмотка с зоной 60° выгоднее, так как

в этом случае векторы э. д. с. катушек группы занимают меньший

угол (см. рис. 20-7) и их геометрическая сумма отличается от их

арифметической суммы меньше (см. рис. 20-8), чем при а = 120°.

В частности, для равномерно распределенной обмотки с зоной

а = 60° или а = л/3, согласно выражению (20-16),

„ = —= I- sin 30° = | = 0,955,

у я я я

2^3

а с зоной а = 120° или а = 2я/3

2л

'2ТЗ

роо -

sin 60° = 0,955 0,867 = 0,828,

т. е. при а = 120° э. д. с. в 0,955 : 0,828 = 1,15 раза меньше и для

получения такой же э. д. е., как и при а = 60°, количество витков

и меди необходимо увеличить на 15%.

Вследствие сказанного на практике предпочитают применять

трехфазные обмотки с зоной 60°, а обмотки с зоной 120 исполь-*

зуют в особых случаях. Очевидно, что соединенная с коллектором

обмотка якоря трехфазной коллекторной машины (см. рис. 19-2Ц

имеет а = 120°. По числу фазных зон на протяжении 2т обмотки

с зоной 60° называются также шестизонными, а с зоной 120° — трех'

зонными.

В общем случае m-фазную обмотку (т 3) также можно выпол-

нить с двумя различными фазными зонами:

а = я/m; а = 2 я/т. (20-22)

В первом случае на протяжении 2т имеется 2т фазных зон (2т-

зонная обмотка), а во втором — m зон (m-зонная обмотка). Очевидно^

что первый случай более выгоден и для него, согласно выражению

(20-15),

При этом

(20-23)

(20-24)

представляет собой число пазов на полюс и фазу,

а выражение (20-21) можно записать также в следующем виде:

(20-25)

Значения коэффициентов распределения обмотки для трехфаз-

ных обмоток с фазной зоной 60° для основной гармоники (v = 1)

и высших гармоник приведены в табл. 20-1.

Таблица 20-1

Коэффициенты распределения fe

шестизониых трехфазных обмоток

3 4 В 6 со

0,966

0,960

0,667

0,958

0,957

0,955

0,707

0,960

0,667

0,654

0,646 0,644

0,636

0,259

0,217 0,205

0,200

0,197

0,191

—0,259

—0,177

—0,158

-0,149

—0,145

—0,136

—0,707 —0,333 —0,270

—0,247

-0,236

-0,212

—0,966

-0,177

—0,126

-0,110

—0,102

—0,087

—0,966

0,217

0,126

0,102 0,092

0,073

—0,707

0,667

0,270

0,200 0,172

0,127

-0,259

0,960

0,158

0,102

0,084

0,056

0,259

0,960

-0,205

-0,110

—0,084 -0,050

21 0,707

0,667

-0,654

—0,247

—0,172

—0,091

0,966 0,217

—0,958 -0,149 —0,092 —0,041

0,966

—0,177

—0,958

0,200 0,102

0,038

0,707

—0,333 —0,654 0,646 0,236

0,071

29 0,259

-0,177

—0,205

0,957

0,145

0,033

-0,259 0,217

0,158

0,957

—0,197

—0,051

—0,707 0,667 0,270

0,646 —0,644

—0,058

—0,966

0,960

0,126

0,200

—0,957 -0,027

—0,966 0,960

—0,126

—0,149

—0,957

0,026

—0,707

0,667 —0,270

—0,247 —0,644

0,049

—0,259

0,217

—0,158

—0,110 —0,197

0,023

0,259

-0,177 0,205

0,102 0,145 -0,022

0,707

—0,333

0,654

0,200

0,236

0,102

—0042

0,966

-0,177 0,958

0,102

0,236

0,102 -0,020

Э. д. с. двухфазной обмотки. В машинах специального назна-

чения нередко применяются двухфазные обмотки (гп = 2), в кото-

рых э. д. с. фаз сдвинуты на 90°. Такие обмотки также выполняются

с заполнением всех пазов (см. рис. 21-20), и фазная зона а = 90°.

При этом для и

пригодны формулы (20-23) и (20-24).

Э. д. с. однофазной обмотки. Обмотку однофазной машины

можно выполнить с заполнением всех пазов машины. Катушечная

группа, или фазная зона, при этом занимает целое полюсное

деление и а = 180° или а = я, причем, согласно выражению (20-16),

V = 1V2-

= 0

637

Таким образом, в этом случае коэффициент k

мал, так как

складываются векторы э. д. с. катушек, занимающие большой угол

(см. рис. 20-7 и 20-8). Это невыгодно, и поэтому обычно применяют

однофазные обмотки, заполняющие две трети пазов машины. При

2 2

этом фазная зона занимает дти

<х

= 120° или а = ^п. В данном

случае в соответствии с выражением (20-16)

V=-S# = t

sin60

° =

828

и для получения одинаковых э. д. с. потребуется в 0,828 : 0,637 =

= 1,32 раза меньше активных проводников или витков.

Соотношения, приведенные выше, действительны также в случае,

когда синусоидально распределенное магнитное поле неподвижно

относительно обмотки, но изменяется во времени или пульсирует

по синусоидальному закону с частотой f.

§ 20-2. Э. д. с. обмотки от высших гармоник

магнитного поля

Полученные в § 20-1 выражения нетрудно распространить на

э. д. с. £

, индуктируемую в обмотке высшей пространственной

гармоникой магнитного поля (см. рис. 20-1). Действительно, полюс-

ное деление v-гармоники x

в v раз меньше т, и поэтому, если сдвиг

двух проводников витка относительно основной гармоники (v = 1)

составляет угол Ря, то относительно v-й гармоники этот сдвиг равен

vfijt (см. рнс. 20-4). В результате при определении коэффициента

укорочения для v-й гармоники"вместо выражения (20-7) надо поль-

зоваться равенством

(20-26)

Сдвиг фаз э. д. с. соседних катушек группы также будет

в v раз больше (см. рис. 20-6, 20-7 и 20-8), и поэтому

коэффициент распределения надо вычислять не по (20-15) и

(20-23), а по формулам:

(20-27)

(20-28)

Аналогично угол скоса паза относительно поля v-й гармоники

(см. рис. 20-2) также будет в v раз больше, и поэтому вместо выраже-

ния (20-3) для коэффициента скоса получим

(20-29)

Обмоточный коэффициент для высшей гармоники

Ao6V AyV^pV'

(20-30)

Отдельные сомножители £

оС

„ k

, и произведение £

o6v

в целом

при вычислениях по приведенным формулам могут получиться отри-

цательными. Это будет означать поворот фазы £

на 180° по сравне-

нию со случаем, когда произведение k

положительно.

Вместо выражения (20-19) для э, д. с. фазы от высшей гармоники

поля будем иметь

Ey,

= nV 2 А

(20-31)

При этом поток v-й гармоники определяется по выражению, анало-

гичному (20-9):

2 2

—

Bfiv^Tv = — B

(20-32)

Здесь принято во внимание, что полюсное деление для v-й гармоники

в v раз меньше полюсного деления основной гармоники.

Частота э. д. с. от высшей гармоники поля f

зависит от скорости

вращения этой гармоники. Например, все гармоники поля возбужде-

ния синхронной машины (см. рис. 20-1) вращаются со скоростью

вращения полюсов, т. е. с одинаковой скоростью. Однако число

полюсов v-й гармоники в v раз больше, и поэтому в данном случае

fv = tf, т. е. высшие гармоники поля индуктируют э. д. с. высших

частот или высшие гармоники э. д. с. В других случаях все э. д. с.

могут иметь одинаковую частоту (см. § 23-2).

Если э. д. с. от различных гармоник поля имеют различные

частоты, то действующее значение суммарной, или полной, э. д. с.

Ez + + .. + ££ + ••. (20-33)

§ 20-3. Улучшение формы кривой э. д. с.

Постановка вопроса. Если, как, например, в синхронных маши-

нах высшие пространственные гармоники поля возбуждения индук-

тируют в обмотке высшие временные гармоники э. д. е., то полная

э. д. с. обмотки будет изменяться во времени несинусоидально.

Как уже указывалось (см. § 13-1), высшие гармоники э. д. с.

могут вызвать в электрических сетях и приемниках ряд нежелатель-

ных явлений. Поэтому необходимо принять меры к их подавлению.

Первой из таких мер является улучшение формы кривой распре-

деления самого магнитного поля и ее приближение к синусоидаль-

ной. Такая мера в отношении явнополюсной синхронной машины

рассматривалась в начале §20-1. Однако получить вполне приемле-

мые результаты при этом не удается.

Поэтому стремятся подавлять высшие гармоники э. д. с.

с помощью соответствующей конструкции обмоток. К таким кон-

структивным мерам относятся: 1) укорочение шага обмотки;

2) распределение обмотки по пазам таким образом, чтобы число

катушек в катушечной группе было q > 1; 3) скос пазов обмотки.

Рассмотрим этот вопрос подробнее.

Э. д. с. от третьей гармоники поля. Три фазы обмотки А, В,

С сдвинуты относительно друг друга по отношению к гармонике

поля v = 1 на 120°, по отношению к гармонике v = 3 на 3 -120

= 360° или 0°, по отношению к гармонике v = 5 на 5-120° = 600°

или 240°, по отношению к гармонике v = 7 на 7 «120° = 840° или

120° и т. д. (рис. 20-10). На такие же углы сдвинуты соответствую-

щие гармоники э. д. с. этих фаз. Таким образом, э. д. с. гармоник

v = 3 и кратных им (v = 9, 15, 21 и т. д.) в разных фазах обмотки

совпадают по фазе и поэтому при соединении обмотки в звезду

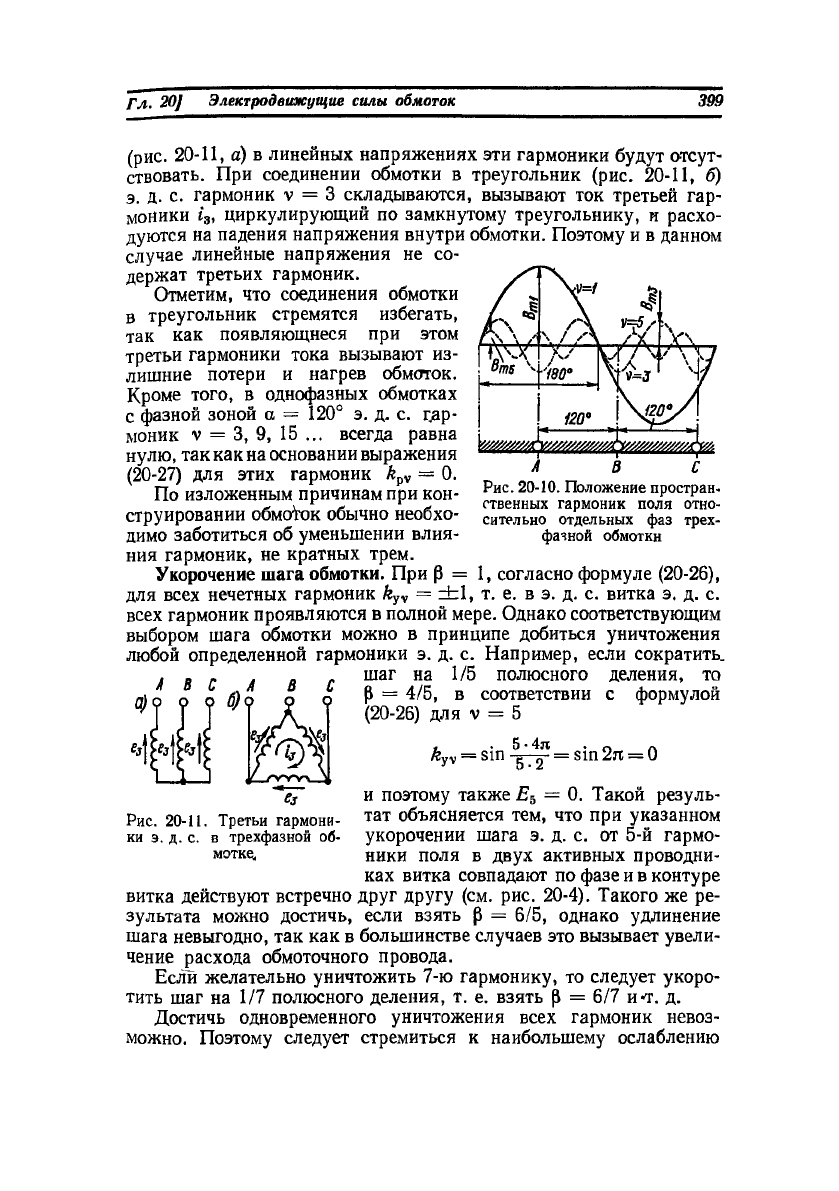
(рис. 20-11, а) в линейных напряжениях эти гармоники будут отсут-

ствовать. При соединении обмотки в треугольник (рис. 20-11, б)

э. д. с. гармоник v = 3 складываются, вызывают ток третьей гар-

моники i

, циркулирующий по замкнутому треугольнику, и расхо-

дуются на падения напряжения внутри обмотки. Поэтому и в данном

случае линейные напряжения не со-

держат третьих гармоник.

Отметим, что соединения обмотки

в треугольник стремятся избегать,

так как появляющиеся при этом

третьи гармоники тока вызывают из-

лишние потери и нагрев обмоток.

Кроме того, в однофазных обмотках

с фазной зоной а = 120° э. д. с. гар-

моник v = 3, 9, 15 ... всегда равна

нулю, так как

на

основании выражения

(20-27) для этих гармоник k

= 0.

По изложенным причинам при кон-

струировании обморок обычно необхо-

димо заботиться об уменьшении влия-

ния гармоник, не кратных трем.

Укорочение шага обмотки. При Р = 1, согласно формуле (20-26),

для всех нечетных гармоник k

= ±1, т. е. в э. д. с. витка э. д. с.

всех гармоник проявляются в полной мере. Однако соответствующим

выбором шага обмотки можно в принципе добиться уничтожения

любой определенной гармоники э. д. с. Например, если сократить.

шаг на 1/5 полюсного деления, то

Р = 4/5, в соответствии с формулой

(20-26) для v = 5

, . 5

•

4л .

п п

fty

= sin -g-g- =

Sln

2п = 0

и поэтому также Е

= 0. Такой резуль-

тат объясняется тем, что при указанном

укорочении шага э. д. с. от 5-й гармо-

ники поля в двух активных проводни-

ках витка совпадают по фазе

в контуре

витка действуют встречно друг другу (см. рис. 20-4). Такого же ре-

зультата можно достичь, если взять р = 6/5, однако удлинение

шага невыгодно, так как в большинстве случаев это вызывает увели-

чение расхода обмоточного провода.

Если желательно уничтожить 7-ю гармонику, то следует укоро-

тить шаг на 1/7 полюсного деления, т. е. взять р = 6/7 и-т. д.

Достичь одновременного уничтожения всех гармоник невоз-

можно. Поэтому следует стремиться к наибольшему ослаблению

ABC

Рис. 20-10. Положение простран-

ственных гармоник поля отно-

сительно отдельных фаз трех-

фазной обмоткн

Л В С Л

09 9 9 0?

Рис. 20-11. Третьи гармони-

ки э. д. с. в трехфазной об-

мотке,

наиболее сильных гармоник, которыми обычно являются гармоники

наименьшего порядка, т. е. v = 5 и v = 7, Для этой цели подходит

укорочение шага на

-Jr

т, когда р = 5/6 = 0,833. При этом

= sin = sin375® = sin 15° = 0,259

= sin

j? 2**° ~

525° = sin

165°

= 0,259,

т. е. э. д. с. этих гармоник уменьшаются почти в четыре раза по

сравнению со случаем, когда р = 1. В то же время при р = 5/6

i = = sin = sin 75°

—

0,966,

т. е. основная гармоника э. д. с. уменьшается незначительно.

Укорочение шага возможно только на целое число зубцовых

делений. Поэтому не всегда можно иметь р = 5/6 и обычно берут

Р = 0,80 -г- 0,86.

Распределение обмотки. При 9=1, согласно выражениям

(20-27) и (20-28), для всех гармоник k

= ±1 и поэтому ослабления

гармоник э. д. с. в обмотке за счет ее распределения в пазах не про-

исходит. Однако если q > 1, то для многих гармоник | &p

| < k

(см. табл. 20-1) и э. д. с. соответствующих гармоник значительно

уменьшаются. Это объясняется тем, что э. д. с. катушек катушеч-

ной группы для v-й гармоники сдвинуты на углы vy вместо углов

у для v = 1 (см. рис. 20--6, 20-7 и 20-8), в результате чего эти э. д. с.

складываются под большими углами и их сумма уменьшается. В то

же время, как видно из табл. 20-1, для v = 1 значения k

= k

близки к единице, т. е. распределение обмотки мало влияет на основ-

ную гармонику э. д. с.

Гармоники зубцового порядка и скос пазов. Из табл. 20-1 видно

также, что и при q >

для ряда гармоник k

= ±k

(числа, выде-

ленные жирным шрифтом), т. е. ослабления э. д. с. этих гармоник

не происходит. Такие гармоники v = v

называются гармо-

никами зубцового порядк_а. Их порядок

= 2 mqk±

= k

± 1,

(20-34)

где k = 1, 2, 3, ....

полюсов Zip, чем

обмотки

при k = 1 близок к количеству зубцов на пару

и обусловлено их название. Для трехфазной

= &qk± 1.

(20-35)