Voit J. The Statistical Mechanics of Financial Markets

Подождите немного. Документ загружается.

4.5 Option Pricing 89

For a variety of reasons which are the principal motivation of the re-

mainder of this book, the traded prices of options usually diﬀer from their

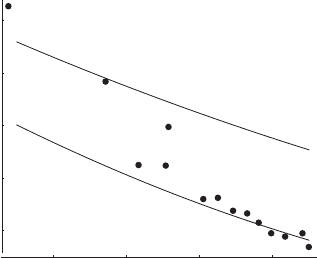
Black–Scholes prices. This is shown in Fig. 4.12 for a series of European calls

on the DAX with a lifetime of one month to maturity. The horizontal axis

“moneyness”, m = X/S, represents the dimensionless ratio of strike price

over underlying. For comparison, the Black–Scholes solution is also displayed

as solid lines. The upper line uses a volatility of 35%y

−1/2

, while the lower

one takes 20%y

−1/2

. Under the assumptions of the Black–Scholes theory and

geometric Brownian motion, a single value of the volatility should be suﬃ-

cient to describe the entire series of call options, and the prices should fall on

one of the solid lines. Figure 4.12 rejects this hypothesis for real-world option

markets.

In the absence of an accurate ab initio estimation of the volatility, a rough

and pragmatic procedure consists in taking the traded prices for granted and

invert the Black–Scholes equation (4.85) for the implied volatility σ

imp

[10]

market

(S, t; r, σ; X, T ) ≡ C

(S, t; r, σ

imp

; X, T) . (4.119)

The idea is to pack all factors leading to deviations from Black–Scholes theory,

independently of their origin, into the single parameter σ

imp

. Volatility, any-

way, is diﬃcult to estimate a priori. For the series of options used in Fig. 4.12,

the implied volatilites are shown in Fig. 4.13. Apparently, there are devia-

tions of traded option prices from a Black–Scholes equation which depend

on the contract to be priced. In this representation, they turn into an im-

plied volatility which explicitly depends on the moneyness of the options. In a

purist perspective, implied volatility adds nothing new to the theory of option

0.98 0.99 1 1.01

moneyness

0.02

0.03

0.04

0.05

0.06

call price

Fig. 4.12. Prices of a series of European call options on the DAX index with

one month to maturity, given in units of the index value, against moneyness X/S

(dots). The two solid lines represent the dependence of the Black–Scholes solutions

on moneyness with two volatilities σ = 35%y

−1/2

(top) and σ = 20%y

−1/2

(bottom)

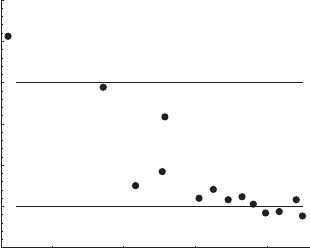
90 4. Black–Scholes Theory of Option Prices

0.98 0.99 1 1.01

moneyness

0.15

0.2

0.25

0.3

0.35

0.4

0.45

implied volatility

Fig. 4.13. Implied volatilities of a series of European call options on the DAX index

with one month to maturity, against moneyness X/S (dots)in%y

−1/2

. Geometric

Brownian motion and the Black–Scholes theory take volatility independent of the

option contract to be priced. The two solid lines mark the contract-independent

volatilities used to generate the solid lines in Fig. 4.12

pricing, and might even lead to confusion. However, it is a simple transforma-

tion of option prices and therefore is an observable on equal footing with the

prices. This is similar to physics: When temperature is measured, the basic

observable most often is an electric current or voltage drop, or height of a

mercury column, etc., which then is transformed into a temperature reading

with a suitable calibration. Also, implied volatility is the standard language

of derivatives traders and analysts to describe option markets.

The generic shapes of implied volatilities against moneyness are shown in

Fig. 4.14. Apparently, a pure smile was characteristic of the US option mar-

kets before the 1987 october crash [53]. Ever since, it has become a rather

smirky structure. The aim of market models more sophisticated than geomet-

ric Brownian motion and of option pricing theories beyond Black–Merton–

Scholes, can be restated as to correctly describe implied volatility smiles.

When a series of options with the same strike price but diﬀerent maturities

is analyzed, a term structure (maturity dependence) of the implied volatility

is obtained in complete analogy to its moneyness dependence. The volatility

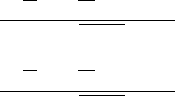
smile turns into a two-dimensional implied volatility surface. Figure 4.15

shows a series of cuts through an implied volatility surface of European call

options. Unlike Fig. 4.13, these curves do not represent market observations

but are the results of a model calculation. Superﬁcially, the one-month curve

is not dissimilar to the empirical data, suggesting that theoretical models

indeed may be capable of correctly describing option markets. Attempts to ﬁt

volatility smiles for a ﬁxed time to maturity usally employ quadratic functions

with diﬀerent parameters for in- and out-of-the-money options, to account

for the systematic asymmetry [53].

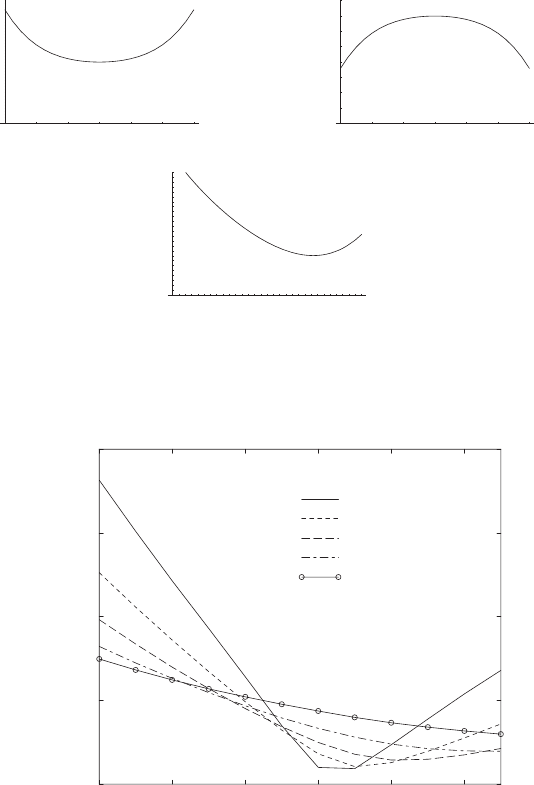
4.5 Option Pricing 91

0.7 0.8 0.9 1 1.1 1.2 1.3

moneyness

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

implied volatility

0.7 0.8 0.9 1 1.1 1.2 1.3

moneyness

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

implied volatility

0.7 0.8 0.9 1 1.1 1.2 1.3

moneyness

0.1

0.2

0.3

0.4

0.5

implied volatility

Fig. 4.14. Sketches of implied volatilities against moneyness. Three generic shapes

can be observed: a smile (top left), a frown (top right) and a smirk resp. skewed

smile (bottom). In equity markets, the smirk is observed most frequently. Often,

the term “volatility smile” includes all three shapes

0.7 0.8 0.9 1.0 1.1 1.2

moneyness

0.6

0.4

0.5

0.3

0.2

implied volatility

1 month

3 months

6 months

1 year

2 years

Time to maturity

Fig. 4.15. Term structure and moneyness dependence of the implied volatility of

a series of European call options based on a model calculation

With reference to the subsequent chapters where we will develop an in-

depth description of ﬁnancial markets, the main handles on the volatility

smiles and term structures are:

• The ordinate scale is determined by the average volatility of the mar-

ket/model.

92 4. Black–Scholes Theory of Option Prices

• Smiles or frowns are the consequence deviations of the actual return distri-

butions, especially in their wings, from the Gaussian assumed in geometric

Brownian motion.

• The skew in the implied volatility is the consequence either of a skewness

(asymmetry) of the return distribution of the underlying or of return–

volatility correlations.

• The term structure of the volatility smiles is determined by the time scales

(or time-scale-free behavior) of the important variables in the problem.

Figures 4.12 and 4.13 show the option prices and implied volatilites of

DAX options on one particular trading day. Both quantities show an inter-

esting dynamics when studied with time resolution. The price of a speciﬁc

option, of course, possesses a dynamics because of the variation in the price of

the underlying. When the prices of a series of options are represented in terms

of moneyness, however, these variations are along the price curve C(X/S)

once the eﬀects of changing time to maturity are eliminated, and should not

lead to dynamical variations of the price curve itself. Additional dynamics

may come, e.g., from the increasing autonomy of option markets which are in-

creasingly driven by demand and supply, in addition to the price movements

of the underlying [54]. One can analyze this dynamics of σ

imp

(m) almost at

the money, m ≈ 1. When, e.g., the time series of σ

imp

(1 − δ) − σ

imp

(1) and

imp

(1) − σ

imp

(1 + δ) are plotted against time, there are long periods where

both stochastic time series are strongly correlated, and other shorter periods

where their correlation is weak [53]. The former correspond to almost rigid

shifts of the smile patterns while the latter appear in periods where the smile

predominantly changes shape. Both time series can be modeled as AR(1)

processes which describes an implied volatility with a mean-reversion time of

about 30 days, comparable to the time to maturity of liquid options.

This line of research can be carried much further by studying the dynami-

cal properties of a two-dimensional implied volatility surface with coordinates

moneyness (m) and time to maturity (T − t) [54]. Implied volatilities are

strongly correlated across moneyness and time to maturity, cf. above, which

suggests a description in terms of surface dynamics. A practical aspect are

trading rules for volatility prediction based on implied volatility. The “sticky

moneyness” rule predicts that the implied volatility surface tomorrow is the

same as that today at constant moneyness and time to maturity. The “sticky

strike” rule stipulates that the implied volatility tomorrow is the same as

today at constant strike and constant maturity (i.e. absolute quantities).

Volatility surfaces can be generated for various series of liquid options

such as calls and puts on the S&P500, the FTSE, or the DAX. With a

generalization of principal component analysis – a technique widely used in

image processing – the implied volatility surfaces can be described as ﬂuc-

tuating random surfaces driven by a small number of dominant eigenmodes.

These eigenmodes parameterize the shape ﬂuctuations of the surface. Their

ﬂuctuating prefactors describe the amplitude of surface variations. The ﬁrst

4.5 Option Pricing 93

eigenmode which accounts for about 80% of the daily variance of the implied

volatility surface is a ﬂat sheet in σ

imp

−m −(T −t) space, almost indepen-

dent of T − t and with a small positive slope in m. This mode essentially

has the same properties as the time series discussed in the second preceding

paragraph. It is also negatively correlated with the price of the underlyings,

i.e. contributes to a “leverage eﬀect” to be discussed in Sect. 5.6.3. The sec-

ond eigenmode changes sign at the money and is positive for m>1and

negative for m<1. A positive variation of this mode increases the volatili-

ties of out-of-the money calls and descreases it for out-of-the-money puts. It

contributes to the skewness of the risk-neutral distributions (when thinking

backwards from implied volatility to risk-neutral measures) and, due to its

slope in T − t, to the term structure. It also possesses the dynamics of a

mean-reverting AR(1)-process. The third mode is a butterﬂy modes which

changes the convexity of the implied volatility surface. It leads to a fattening

of the tails of the risk-neutral distributions, cf. the mechanistic rules listed

above [54].

This dynamics can be cast in a low-dimensional factor model

X(t; m, T −t) ≡ ln σ

imp

(t; m, T −t)=X(0; m, T −t)+



k=1

(t)f

(m, T −t) .

(4.120)

is one of the d dominant eigenfunctions of the principal component decom-

position. They are time-independent and describe the spatial variation of the

ﬂuctuations. The dynamics comes from the randomly ﬂuctuating prefactors

(t) which, according to the ﬁndings above, can be modeled as Ornstein-

Uhlenbeck processes

(t)=−λ

(t) − ¯x

]dt + γ

. (4.121)

is the rate of mean reversion and ¯x

is the average of the k

eigenmode.

The stochastic increments dz

are uncorrelated and may be drawn from a

Gaussian (consistent with the lognormal distribution of implied volatilites, cf.

below) or a more general distribution. The ranks of the ﬂuctuating expansion

coeﬃcients x

(t) in (4.120) are ordered according to their variances γ

which

measures the amplitude of the ﬂuctuations they impart on σ

imp

(t; m, T −

t). The dynamics of the implied volatility surfaces analyzed above can be

faithfully represented by three factors x

(t) ...x

(t) [54].

4.5.8 Volatility Indices

Volatility is the most important and least accessible quantity in option the-

ory. Volatility can be inferred either from historical time series [estimate

σ in (4.53)] or from implied volatility of options by inverting the Black–

Scholes equation as in (4.119). For derivative markets, the second method

is preferrable because the information is derived directly from derivative

94 4. Black–Scholes Theory of Option Prices

instruments, and implied volatility is more forward-looking than historical

volatility.

Derivative trading requires high-frequency information on volatility, resp.

implied volatility. The question arises if information on implied volatility can

be provided in a standardized manner to assist traders in their decisions.

Volatility indices have been constructed by various option exchanges to ﬁll

this gap. As volatility often signiﬁes ﬁnancial turmoil, volatility indices play

the role of “investor fear gauges”. In the following, we discuss two two indices

using diﬀerent construction principles.

VDAX Index

The VDAX index is provided by Deutsche B¨orse AG, and measures the im-

plied volatility of at-the-money options on the DAX with 45 days to maturity

[55]. Options on the DAX are among the most liquid instruments in the Eu-

ropean derivatives markets. Although it is not directly relevant for other

options, the knowledge of the VDAX value gives a good indication of the

volatilities traded in the broader derivatives market.

Conceptually, the VDAX is based on implied volatilities, i.e. the Black–

Scholes equation (4.85), resp. (4.86), is inverted numerically as formally done

in (4.119). The practical calculation is more diﬃcult, though, most impor-

tantly because, except for accidental circumstances, no option at the money

with 45 days to maturity is traded in the markets.

Moreover, in practice, the traded futures price on the DAX are used for

the VDAX calculation instead of the DAX itself. For options on futures, the

Black–Scholes equation can be rewritten most easily by equating forward and

futures prices F and using (4.1) in (4.85) and (4.86) to obtain

−r(T −t)

[FN(d

) − XN(d

)] (4.122)

−r(T −t)

[XN(−d

) − FN(−d

)] (4.123)

for the prices of call and put options on futures, respectively. d

and d

diﬀer from (4.88) and (4.89) and are given by





(T − t)

√

T − t

, (4.124)

−





(T − t)

√

T − t

. (4.125)

The risk-free interest rate no longer appears explicitly in (4.124) and (4.125)

and is implicitly accounted for by the use of the futures price F , cf. (4.1).

The Black–Scholes problem for options on futures can also be solved ab initio

following the lines of Sects. 4.5.1 and 4.5.2, with (4.122) and (4.123) as the

4.5 Option Pricing 95

solutions of the modiﬁed diﬀerential equations [10, 56]. This solution is known

as Black’s 1976 model.

The VDAX is based on a set of eight subindices calculated for DAX op-

tions with maturities of up to two years. Each subindex is based on four

at-the-money options for the given maturity. After data ﬁltering, the best

bid and ask prices of each call and put option and of the DAX futures are

averaged. Next, the risk-free interest rate is not a universal constant but de-

pends on the maturity of the bonds it is taken from. Under normal conditions,

r is lower for short-maturity bonds than for long maturities (“normal interest

rate curve”). Only under exceptional circumstances is the interest rate curve

inverted, i.e. the long maturities bring less interest than the short maturities.

In general, risk-free interest rates are not available for the maturities of the

options considered. In practice, they are generated by linear interpolation

from two values bracketing the option contract maturity.

When the maturity of futures contracts diﬀers from that of options, put-

call parity is used to generate an eﬀective forward price from the option

prices. Using (4.1), (4.8) for put-call parity can be rewritten in terms of the

forward price as

F (t)=[C(t) − P (t)] e

r(T −t)

+ X. (4.126)

This equation is used for up to eight pairs of options for four strike prices

above and below the “at-the-money point”, and averaged at the end. Once

the forward price is available, (4.122) and (4.123) are inverted for the implied

volatility σ

imp

The implied volatility constituting a volatility subindex for a speciﬁc ma-

turity T

is calculated as a weighted average of the implied volatilities a pair

of put and call options with strike prices bracketing the futures price

imp

− F (T

)]



call

imp,l

+ σ

put

imp,l



+[F (T

) − X

]



call

imp,h

+ σ

put

imp,h



2(X

− X

)

(4.127)

The subscripts h and l label the options with maturity T

above and below

the futures price. The eight volatility subindices are published by Deutsche

B¨orse AG as additional information.

The VDAX then is the implied volatility generated from the two subindices

with maturity closest to 45 days, by interpolation of the variances

VDAX

imp



i+1

− T

i+1

− T

imp

T − T

i+1

− T

imp

i+1

) , (4.128)

where the maturities satisfy

≤ T = 45d <T

i+1

. (4.129)

96 4. Black–Scholes Theory of Option Prices

The VDAX is the implied volatility of a hypothetical at-the-money option

with a 45-day maturity. At the time of writing, the VDAX is quoted every

minute from 9 a.m. to 5:30 p.m.

There have been attempts to create derivatives on the VDAX. It is re-

ported that the pricing and hedging of these products encountered many

diﬃculties. Most likely, it was done in a way similar to that described in the

subsequent text, supplemented by rules of thumb for the inevitable diﬀerences

between the VDAX and the quantity eﬀectively priced and hedged.

VIX

The VIX is the volatility index of the Chicago Board Options Exchange

(CBOE) [57]. It measures the volatility of options on the S&P500 index with

30 days to expiration.

Since its introduction in 1993 until 2003, it was based on the implied

volatility of at-the-money options on the S&P100 index, and calculated in

a manner similar to the VDAX described above. In 2003, the method of

calculation was changed, and the index now refers to the S&P500 index. The

change was made in response to advances in quantitative ﬁnance which were

driven by the desire to trade volatility derivatives deriving their measure of

volatility directly from a series of option prices [57, 58]. Here, we continue to

call this volatility measure “implied volatility” although this formally is not

justiﬁed by (4.119) which we used to deﬁne implied volatility. The labeling is

justiﬁed, however, (i) when implied volatility is understood as the market’s

expectation of future realized volatility, and (ii) by the strong similarity of the

old VIX based on implied volatility, and the new VIX extended backwards

in time to cover the period of the old VIX [57].

To understand the general problem behind the creation of volatility deriv-

atives, notice that the hedging of a derivative, say on option, based on σ

imp

as obtained by (4.119), is a highly nontrivial task. When volatility can be

represented, e.g., as a linear combination of traded instruments, hedging is

much easier.

How can one create an instrument that allows pure trading of volatility?

With a position in an option, an investor is exposed both to the directional

movements of the underlying and to its volatility. Can one eliminate the

exposure to directional moves?

The simplest derivative instrument on volatility is a volatility, or variance

swap. A swap is a contract which exchanges (“swaps”) two cash ﬂows. Swaps

are most common in the ﬁxed income sector (bonds and credits), and often

the parties exchange the cash ﬂows from ﬁxed interest rate payments against

variable interest rate payments. The payoﬀ of a variance swap at expiration

VS(T )=(σ

− K

var

)N, (4.130)

where σ

is the variance of the underlying realized over the lifetime of the

swap, K

var

is variance delivery price and N is the notional of the contract. The

4.5 Option Pricing 97

holder of the swap receives N dollars for every point by which the variance

exceeds the delivery price K

var

[58]. Alternatively, the variance swap may

be understood as a forward contract.

To understand the construction of such a swap, go back to the deﬁnition

of the Vega of an option. Vega, as deﬁned in (4.109) measures the sensitivity

to changes in volatility. The variance exposure of a call option is measured

by the “Variance Vega”

var

∂C

∂σ

√

T − t

√

2πσ

exp



−



, (4.131)

where the second equality is valid only for Black–Scholes option prices, and

was given in (4.88). Variance Vega is peaked at S = X with a peak height

proportional to X due to the explicit prefactor S. When many options with

slightly diﬀerent strikes are superposed with equal weight in a portfolio, the

variance exposure of this portfolio is given by the superposition of the Vari-

ance Vegas. This leads to a triangular shape (in S) with Gaussian roundings

at the edge. When the portfolio weighs the options with a weight factor X

−2

on the other hand, the dependence on S drops out, and the portfolio has an

exposure to variance only (provided the price of the underlying remains in

the range covered by the option strikes). This result becomes exact when

the strike price X is treated as a continuous variable, and the portfolio is

expressed as an integral over X with a weight factor X

−2

[58]. In practice,

out-of-the-money options are more liquid. For this reason, both out-of-the-

money call and put options are used in setting up the portfolio

(t)=





P (X, t)+



∞



C(X, t) . (4.132)



is an arbitrary reference price close to the at-the-money point. This port-

folio’s Delta and Variance Vega are [58]

∆ =

∂Π

(t)

∂S

≡ 0 , V

var

∂Π

(t)

∂σ

T − t

. (4.133)

At expiration, the value of the portfolio Π

(T )is

(T )=





max [X − S(T ), 0] +



∞



max [S(T ) −X, 0]

S(T ) −S



− ln



S(T )





. (4.134)

The ﬁrst term in the second equation essentially is an ordinary forward con-

tract with a payoﬀ linear in the deviation from the reference price S



.The

second term is a log-contract whose payoﬀ equals the logarithm of the price

ratio.

98 4. Black–Scholes Theory of Option Prices

As with any other derivative, the fair delivery price of variance K

var

ﬁxed by the requirement that the expected present value of the future payoﬀ

in a risk-neutral world is zero. The variance realized over the lifetime of the

swap is



dtσ

(t) , (4.135)

where σ – unlike geometric Brownian motion – may be a time-dependent,

perhaps even stochastic quantity. The criterion of zero expected value of the

payoﬀ then translates in

F (t)=e

−r(T −t)

σ

− K

var

 =0. (4.136)

When S(t) follows an Itˆo process (4.40) even with a time-dependent

volatility σ(t), we can combine (4.53) and (4.62) to obtain

dS(t)

S(t)

− d[lnS(t)] =

dt. (4.137)

Insert this into (4.135) and solve the second equality in (4.136)

var



dS(t)

S(t)

− ln



S(T )

S(0)



. (4.138)

For an Itˆo process in a risk-neutral world,



dS(t)

S(t)



rdt + σ(t)dz

= rT . (4.139)

The last term in (4.138) is related to the log-contract in our portfolio of

options with a continuous strike distribution. Combining everything gives

the fair delivery price of the variance swap [58]

var





P (X, t)+e



∞



C(X, t)

+ rT −



S(0)e



− 1



− ln



S(0)



. (4.140)

This derivation does not require geometric Brownian motion, or the validity

of the Black–Scholes assumptions. An instrument trading volatility alone thus

can be constructed based on a weighted portfolio of options with a continuous

strike distribution and weights inversely proportional to X

Clearly, the value of such an instrument is a measure of the market’s

expected volatility over the lifetime of the contract, and therefore constitutes

a valid volatility index. This is precisely what the CBOE’s VIX does. As with

the instruments acutally traded in the markets, the ideal continuous strike