Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

70 Rolf Klein and Tom Kamphans

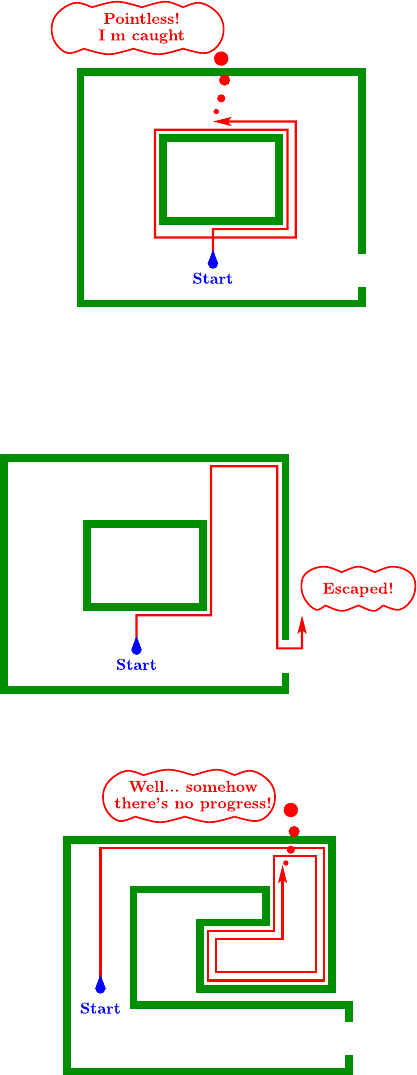
So, our ﬁrst idea does not work in general. We need to leave a pillar

eventually. Next try! Follow our nose until we hit a wall; follow the wall until

we can move straight ahead in the original “nose” direction. Now, the pillar

is no longer a problem:

But this approach does not work in our ﬁrst example.

8 Pledge’s Algorithm 71

“Now it gets scary! Whatever I try, nothing works. But there must be

some way out of here – after all I did get in somehow.”

Of course there is a way out of the maze. We just have to ﬁnd it. So, is

there an algorithm that ﬁnds a path out of every possible maze? Even in the

dark and without any tools such as chalk or GPS?

Amazingly, such an algorithm exists!

Pledge’s algorithm

1 Set angle counter to 0;

2 repeat

3 repeat

4 Walk straight ahead;

5 until wall hit;

6 Turn right;

7 repeat

8 Follow the obstacle’s wall;

9 until angle counter = 0;

10 until exit found;

It is not suﬃcient to just watch the direction of one’s nose; we need to

count the turns that we make while following the walls.

For simplicity, let us assume that all corners are rectangular, as in our

examples. Then there are only left and right turns of 90 degrees each. We

count these turns as follows. For every left turn we add 1 to our counter, for

every right turn we subtract 1 from the counter (in particular, we subtract 1

for the very ﬁrst turn we make when hitting a wall).

This algorithm is said to have been invented by a 12-year-old boy named

John Pledge. And it works! Not only for our examples, but in every maze!

Let’s try to prove this.

Suppose Pledge’s algorithm does not ﬁnd us a way out. Then we get stuck

in a loop that will be followed on and on. Why? There are but a few points

where we may change our direction, the corners of obstacle walls, and from

every corner the ﬁrst point on an obstacle seen in the initial nose direction. If

we reach one of these points twice with the same angle-counter value, the path

between both visits is repeated forever, because our behavior never changes.

Otherwise, we reach every corner at most once with the same angle-counter

value, in particular, with value 0. When all these visits have been made, we

will never again leave the current obstacle, because whenever we can, the

counter won’t be 0. Thus, our path gets cyclic.

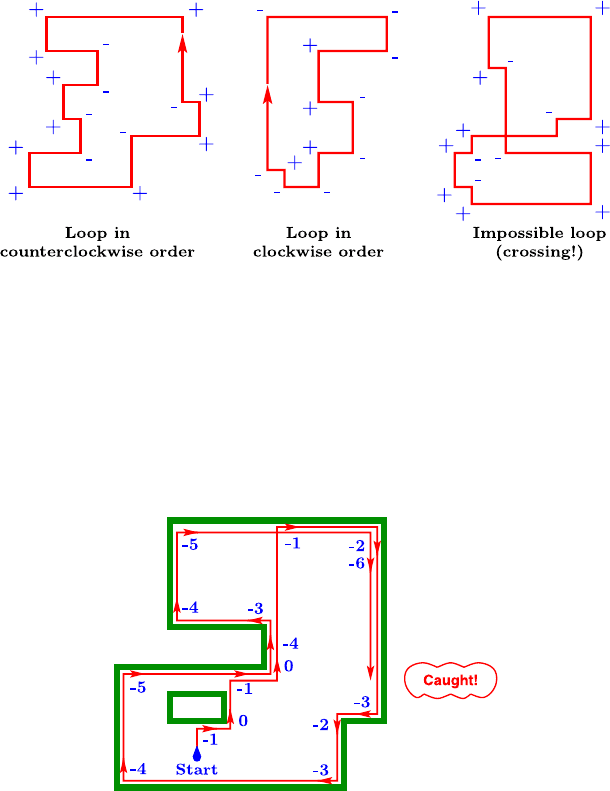
Moreover, we can show that the loop we are following forever can have no

self-crossings. In a crossing, two straight segments of the path – let’s call them

A and B – will meet. One of them – say A – has to be a free segment; that is,

72 Rolf Klein and Tom Kamphans

the segment does not lead along an obstacle wall, because walls of obstacles

do not cross.

Let z be the crossing of A and B and let C



)andC



) be the angle-

counter values in a point z



shortly behind z, having reached z via A and B,

respectively. Then, we have



)=−1,



)=−1+4· k for k ∈ Z,

because right after z our nose points in the same direction. For k ≥ 1, we get



)=−1+4k>0.

But our angle counter value can never become positive. This is because

after hitting a wall the counter has value −1. As soon as it reaches 0, we leave

the wall. After hitting the next wall, it gets negative again, and so on. Hence,

we must have k ≤ 0.

From k = 0 we would conclude C



)=C



). In this case, the parts of

the path along A and B behind z would never separate again. So, if we walk

along segment B, after visiting z, we would never walk along A again – and

vice versa. This contradicts the fact that both A and B are part of an endless

loop.

Thus, only the case k ≤−1 remains. Then, we have C

(t) <C

(t)for

every point t from z



to the point v where both paths split. Moreover, in v we

must have C

(v) = 0. So these parts of the path look as shown in the next

ﬁgure. We do not have a real crossing – the parts of the path just touch each

other.

8 Pledge’s Algorithm 73

So far, we have shown the following. If the Pledge algorithm doesn’t get

us out of a maze, we end up in an endless cycle that has no self-crossings.

Assume that we traverse this loop in counterclockwise direction. Then, we

have four more left turns than right turns, and our angle counter increases

each time we complete a cycle. Eventually, its value must become positive,

but we have already seen that this cannot happen. Thus, we traverse the loop

in clockwise direction. In every pass, our angle counter decreases by 4. That

means, we keep following a wall with our left hand without ever leaving it.

But then we are inside a closed room – and there is no way out!

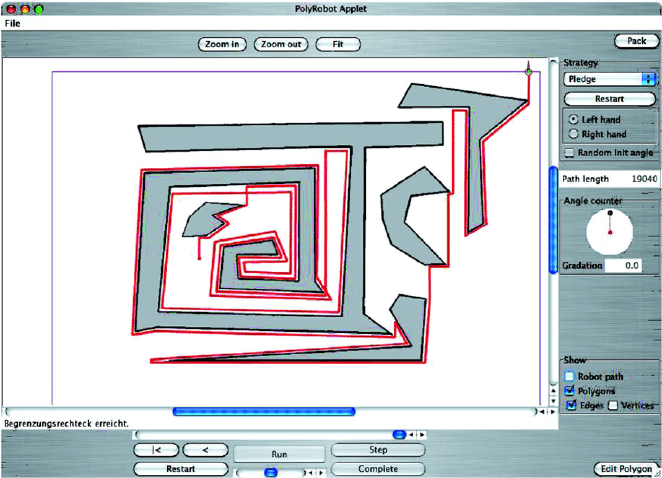
You can use the Java applet http://www.geometrylab.de/Pledge/ to

draw a maze and observe how Pledge’s algorithms deals with it. By the way,

it also works for mazes with non-rectangular angles. In this case, we have to

exactly add the (signed) turning angles instead of just counting the number

of turns.

74 Rolf Klein and Tom Kamphans

Here is an example.

Further Reading

1. Chapter 7 (Depth-First Search)

In this chapter, you learn how to use additional tools such as threads or

chalk.

2. Chapter 9 (Cycles in Graphs)

helps to prevent you running around in a circle.

The “nodes” mentioned in this chapter are rooms in our mazes with more

than one exit. The “edges” are tunnels and doors that connect two rooms.

3. http://www.geometrylab.de/Pledge/

Here, you can try out Pledge’s algorithm with a Java applet. Moreover,

you’ll ﬁnd a short movie showing a small robot (a Khepera II) which uses

Pledge’s algorithm to solve a maze.

4. Rolf Klein: Algorithmische Geometrie: Grundlagen, Methoden, Anwen-

dungen. Springer, Heidelberg, 2nd edition, 2005 (in German).

Harold Abelson, Andrea A. diSessa: Turtle Geometry. MIT Press, Cam-

bridge, 1980.

In these books you’ll ﬁnd the proof that Pledge’s algorithm also solves non-

rectangular mazes. Moreover, similar problems are presented; for example,

how a robot can ﬁnd a target point.

8 Pledge’s Algorithm 75

5. Bernd Br¨uggemann, Tom Kamphans, Elmar Langetepe: Leaving an un-

known maze with one-way roads.In:Abstracts 23rd European Workshop

Comput. Geom., 2007, pp. 90–93.

http://web.informatik.uni-bonn.de/I/publications/bkl-lumow-

07.pdf

Unfortunately, Pledge’s algorithm does not work if there are passages that

can be traversed in only one direction (e.g., one-way roads). This paper

shows how you can escape anyway.

Acknowledgement

The authors thank Martin Dietzfelbinger for many valuable comments.

Cycles in Graphs

Holger Schlingloﬀ

Humboldt-Universit¨at zu Berlin, Berlin, Germany

This chapter is about cycles in graphs. We want to ﬁnd a way to tell whether

there is a cycle in a set of nodes which are connected by edges. A cycle is a

path which leads from one node back to itself.

Scenario 1

Imagine you were on an airplane

that crashed in the middle of the

jungle and now you’re trying to

ﬁnd a way back into civilization.

There are some paths through the

jungle that were created by na-

tives; other than those, there is

only coppice around you. The veg-

etation is so dense that you can’t

even see the sky, let alone the sun.

You pack your belongings, choose

one of the paths and start head-

ing in that direction. After a lit-

tle while, there is a fork in the

path.

You decide to turn right. Then

you encounter a junction where you keep walking straight ahead. Unfortu-

nately, this leads you to a dead end: you have to turn around and go back

to the intersection, where you now turn. At the next fork, you take the left

path, then the right, and so on. Suddenly, there is a clearing in the jungle and

you see your airplane, your starting point. Apparently, you’ve been walking

in circles all the time. How can you avoid getting lost again, what would be

a better way to try to return to civilization?

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

 Springer-Verlag Berlin Heidelberg 2011

78 Holger Schlingloﬀ

Scenario 2

Andy wants to go to the movies with Benny and Charly. Charly, however,

has to babysit at home and can only leave when Dany comes and takes over.

Benny may only go when he is ﬁnished with his homework. He also needs

help from Dany, who has promised to come over as soon as Eddy returns her

book, which he borrowed from her in school. Eddy himself is still racking his

brains about the homework questions and hopes that Benny will send him an

e-mail with the solutions. Why will Andy probably not get to see the movie

with Benny and Charly tonight?

Both scenarios demonstrate the same problem: cycles in graphs. A directed

graph is a structure that consists of nodes and edges, where an edge leads from

one node to another. In order to visualize a graph, nodes are shown as circles

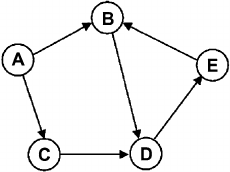
and edges as arrows between nodes. For this example, we can draw a node

for each person and an edge from node x to node y if person x is waiting for

person y. We write A for Andy, B for Benny, C for Charly, and so on. The

graph for scenario 2 then looks like this:

Obviously, there is a cycle in this graph: B → D → E → B. That means

there is a sequence of nodes connected by edges where the beginning and

the end of the path are the same node. Benny is waiting for Dany, Dany

is waiting for Eddy, and Eddy is waiting for Benny: if they don’t do any-

thing about it, they will wait for each other for a very long time. Cycles like

the one shown here can lead to problems such as endless processes (as in

the ﬁrst scenario, where you can walk through the jungle endlessly) or pro-

cesses getting stuck (as in the second scenario, where no one will see the

movie unless someone dissolves the cycle). When this happens in a com-

puter program, it is called an endless loop (if the process runs endlessly)

or a deadlock (if the process gets stuck). In both cases, usually the program

fails to show a reaction and has to be ended from the outside, e.g., by the

user. This is why it is important to recognize cycles and, if possible, avoid

them.

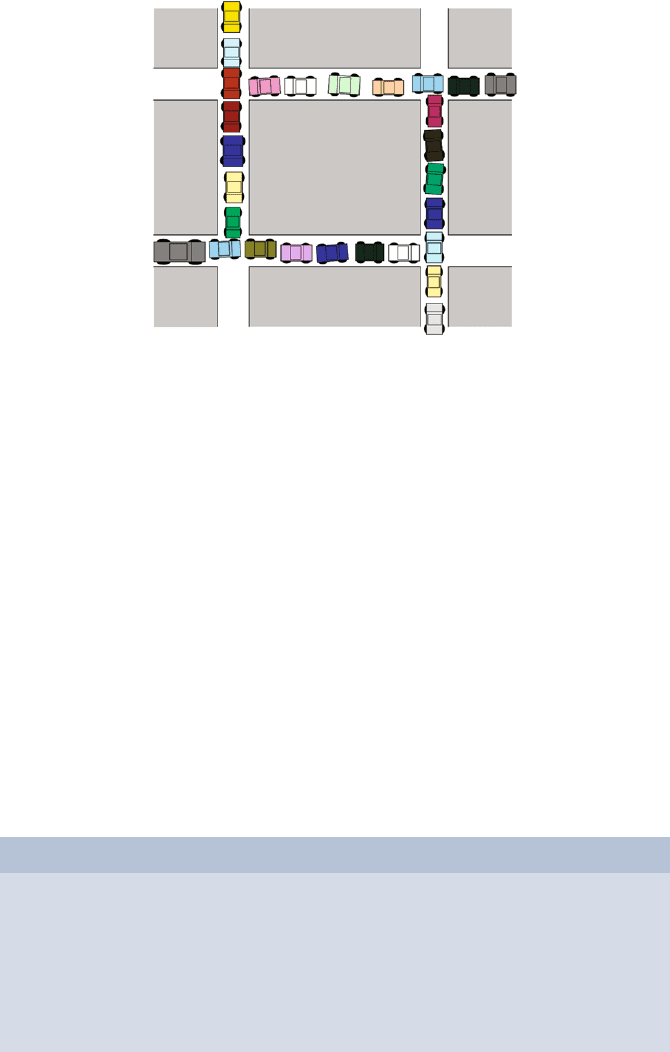
9 Cycles in Graphs 79

A traﬃc deadlock

Finding Cycles by Depth-First Search

So how can we actually ﬁnd cycles in a program? Let’s look at the ﬁrst scenario

again: you’re lost in the jungle, trying to ﬁnd a way out. If you want to avoid

running in circles, you could use the same trick Hansel and Gretel came up

with in the well-known fairytale and mark your way through the dense forest

with pebbles. If you then come across a pebble that you dropped before, you

know right away that you’ve been there already and that this way is not

going to get you out. Basically, this is the same situation that was described

in Chap. 7, where Theseus, trying to ﬁnd his way through the labyrinth, marks

his path with the thread Ariadne gave him (or, alternatively, with chalk). In

order to simulate our jungle expedition with a computer program, we can use

depth-ﬁrst search (DFS), as in Chap. 7. First, we describe the jungle map with

a graph: every fork or intersection in the path is a node in the graph, every

stretch of road in between is an edge. The goal of the search is to ﬁnd a node

which is outside the jungle. We can write the algorithm for our depth-ﬁrst

search down like this (quite similarly to the algorithm in Chap. 7):

Depth-ﬁrst search

1 procedure depth-first-search (node x)

2 begin

3 if goal is reached then stop

4 else if x is unmarked then

5markx;

6 for all nodes y succeeding x do depth-first-search(y) endfor

7 endif

8 end