Vocking B., Alt H., Dietzfelbinger M., Reischuk R., Scheideler C., Vollmer H., Wagner D. Algorithms Unplugged

Подождите немного. Документ загружается.

80 Holger Schlingloﬀ

Here we assume that all nodes are “unmarked” in the beginning. The

depth-ﬁrst search begins when the procedure depth-first-search(x

)is

started for any node x

.Ifx

is followed by the nodes y

, y

, etc., depth-

first-search(y

), depth-first-search(y

), and so on, will be started in

order. However, if for example y

has the successor nodes z

, z

, etc., then

depth-first-search(z

), depth-first-search(z

), and so on, will be com-

pleted for all z before depth-first-search for y

is started. If the search

leads to a node that doesn’t have any successors (a dead end), or a node that

has already been marked, the search is not continued, but will return to the

previous node, and so on.

For our jungle scenario this means that at an intersection you drop a

pebble and then systematically test all possible paths which start from this

intersection. If you reach a dead end at one path, or see a pebble lying on

the ground that you know you dropped before, you return to the previous

intersection and try another path from there. This makes more sense than

just randomly following any path and then, if it reaches a dead end or be-

comes cyclic, returning all the way to the starting point to try a diﬀerent

path.

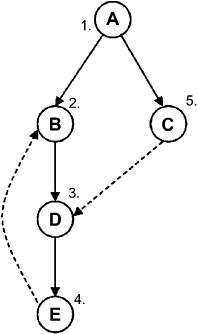
This picture illustrates the algorithm for our sec-

ond scenario, in which Andy is trying in vain to

catch a movie with his friends Benny and Charly.

The nodes (which here represent the people in-

volved) are drawn in order from top to bottom (from

A to E); the numbers next to the nodes show the

order in which the nodes are reached and marked by

the algorithm. The search starts with node A, and

therefore with the call depth-first-search(A).

Since A is not marked yet, depth-first-search(B)

and depth-first-search(C) are started in order.

depth-first-search(C) will run after depth-first-

search(B) and depth-first-search of all suc-

cessors of B are completely ﬁnished. depth-first-

search(B) calls depth-first-search(D), which

calls depth-first-search(E), which calls depth-

first-search(B), since B is a successor of E. Node B, however, is already

marked; therefore, we go back to the previous node, E. This node does not

have any other successors than B. Therefore, we return to D, then to B, and

then to A. Here we see that A actually has another successor that has not

been called yet, C; therefore, depth-first-search(C) is started now. The

only successor of C, node D, is already marked, so we return to C and then

to A. Now all calls are ﬁnished and the algorithm is done.

When trying to ﬁnd cycles in graphs, the goal is to discover whether

or not a graph contains any cycles, and, if possible, have one (or some) of

9 Cycles in Graphs 81

them displayed. In order to achieve this, we need to adjust our algorithm

a bit. As we can see in our example graph above, there are three kinds of

edges:

1. forward edges, such as A → C

2. sideward edges, such as C → D, and

3. backward edges, such as E → B.

In a directed graph, only an edge that goes backwards can cause a cycle.

Backward edges diﬀer from edges that go sideways in that they lead to nodes

that have not been completely processed yet. We can include this informa-

tion into the above algorithm if we extend the markings: instead of just

“marked” or “unmarked,” we can have the program ‘remember’ whether

the processing of a node has not started yet, is in progress, or is done.

(In our jungle scenario, we could use pebbles of diﬀerent color for this pur-

pose.)

Depth-ﬁrst search for cycles

1 procedure search-cycle (node x)

2 begin

3 if mark(x) = “in progress” then a cycle has been found

4 else if mark(x) = “not started yet” then

5mark(x) := “in progress”;

6 for all nodes y succeeding x do search-cycle(y) endfor;

7mark(x) := “done”

8 endif

9 end

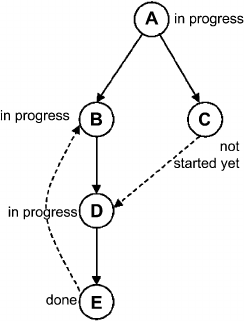
For our example graph, the order of the calls would look like this:

search-cycle(A) // A not started yet

| A in progress

| search-cycle(B) // B not started yet

||Binprogress

||search-cycle(D) // D not started yet

|||Dinprogress

|||search-cycle(E) // E not started yet

||||Einprogress

||||search-cycle(B) // B in progress

|||||acycle has been found!

||||Edone // snapshot

|||Ddone

| | B done

82 Holger Schlingloﬀ

| search-cycle(C) // C not started yet

||Cinprogress

||search-cycle(D) // D done

| | C done

| A done

A snapshot during the execution

of procedure search-cycle

Strongly Connected Components

The algorithm search-cycle that was shown above determines whether a

cycle can be reached from the starting node. However, it cannot recognize

which nodes are part of the cycle. The algorithm can therefore not solve the

deadlock in the second scenario: if no one knows that Benny, Dany, and Eddy

are part of a cycle, they can’t solve their problem.

In order to break the deadlock, we have to determine which nodes are part

of it. To do so, the algorithm has to remember the order of the nodes which

are “in progress”. At the snapshot shown above, the current path is A → B

→ D → E → B, which means that B, D, and E are in the cycle: when a node

is encountered along the path that has already been seen (in this case, B), all

nodes that follow this node (here, D and E) are part of the cycle. Whenever

the algorithm is ﬁnished with a node and returns to the previous node, the

ﬁnished node has to be removed from the current path (as it is obviously not

part of a cycle).

As an algorithm, this idea would look as follows:

9 Cycles in Graphs 83

Finding cycles by depth-ﬁrst search

1 procedure find-cycle(node x)

2 begin

3 if mark(x) = “in progress” then

4 a cycle has been found;

5 all nodes on the current path starting at x are on the cycle

6 else if mark(x) = “not started yet” then

7mark(x) := “in progress”;

8 extend the current search path by appending x;

9 for all nodes y succeeding x do find-cycle(y) endfor;

10 mark(x) := “done”;

11 remove x (the last element) from the current path

12 endif

13 end

Here we assume that at the beginning all nodes are marked as “not started

yet” and that the initial search path is empty.

What would happen in this algorithm if there were more than one cycle

in the graph, for example, an additional edge from D to A (that means Dany

would be waiting for Andy)?

The example graph with an additional edge

In this case, ﬁrstly, we have the cycle B → D → E → B that already

appeared in the graphs before. Additionally, we have the cycle A → C →

D → A, which has a similar structure. Furthermore, there would be other

cycles, such as E → B → D → A → B → D → E. When two nodes are on the

same cycle, we say that they are connected. For example, nodes A and E are

connected if there is a cycle A → ···→E → ···→A somewhere. All nodes

that are connected with each other (that are on one common cycle) form a

strongly connected component (SCC).

Within a strongly connected component, each node can be reached from

every other node. Therefore, if A and E are connected, and there is a path

from A to C, then there must also be a path from E to C. We can imagine a

strongly connected component as a group of nodes which are “similar” with

84 Holger Schlingloﬀ

respect to reachability. The graph that is formed by grouping all nodes of

a strongly connected component is called the quotient graph of the original

graph. A quotient graph does not contain cycles any more. The reason for

this can be seen in the illustration below: if there were a cycle that connected

two strongly connected components, they would ‘melt’ together into one. If

in a graph all nodes are connected with each other (as in the above example

graph with an additional edge), the graph consists of just one single strongly

connected component, and the quotient graph has just one node.

Strongly connected components and quotient graph

Robert E. Tarjan, an American computer scientist (born 1948) who was

given the Turing Award for his work on the design and analysis of algorithms

and data structures in 1986, extended the algorithm find-cycle shown above.

His famous algorithm for strongly connected components made it possible to

ﬁnd not only cycles, but also the strongly connected components that can be

reached from a starting node. In order to do this, every node gets assigned two

numbers: ﬁrstly, the number under which it appears in the order of depth-ﬁrst

9 Cycles in Graphs 85

search, and secondly, the number of the ﬁrst node of the strongly connected

component to which the node belongs.

Strongly connected components

1 procedure find-components (node x)

2 begin

3 if mark(x) = “in progress” then a cycle has been found

4 else if mark(x) = “not started yet” then

5mark(x) := “in progress”;

6 depth-ﬁrst-search-number(x):=counter;

7 component-number(x):=counter;

8 counter := counter +1;

9 extend the current search path by appending x;

10 for all nodes y succeeding x do

11 if mark(y) is not “done” then

12 find-components(y);

13 if component-number(y) < component-number(x) then

14 component-number(x):=component-number(y)

15 endif

16 endif

17 endfor;

18 if depth-ﬁrst-search-number(x)=component-number(x)

then

strongly connected

component has been found;

20 all nodes on the current path with this component-number are

part of the same component

21 for all these nodes y do

22 mark(y) := “done”;

23 remove y from the current path;

24 endfor;

25 endif

26 endif

27 end

The counter is initialized with a ﬁxed value (e.g., 1). An example for the

marks of the nodes after running find-components can be seen in Fig. 9.1.

The quotient graph in this example would have the components 1, 2, and 5;

edges lead from 1 to 2, from 1 to 5, and from 5 to 2.

Searching for Cycles with Breadth-First Search

As we can see, depth-ﬁrst search is very useful for ﬁnding all cycles or strongly

connected components in a graph. However, if the goal is merely to ﬁnd out

whether a given starting node is part of a cycle, we can use a simpler algorithm:

applying the so-called breadth-ﬁrst search, we can determine the set of nodes

that can be reached from our starting node. For this, we assume that we have

86 Holger Schlingloﬀ

Fig. 9.1. Markings of the nodes after running find-components

an eﬃcient method to calculate the set of nodes that are succeeding a given

set of nodes (i.e., that can be reached from a node in this set by an edge). And

then we start our breadth-ﬁrst search: the ﬁrst set of nodes includes only the

starting node, the second set includes all nodes that can be reached from the

starting node, the third set includes all nodes that can be reached from the

nodes of the second set, and so on. At some point, one of the following will

happen: either no more nodes can be reached, or we return to our starting

node. If the latter is the case, we have our answer: the node is part of a cycle;

there is a path that goes from the node back to itself. If the search is done

(that is, no more nodes can be reached), and we have not encountered the

starting node, then it is obviously not part of a cycle.

Breadth-ﬁrst search

1 procedure breadth-first-search (node x)

2 begin

3 reachable := {}; front := {x};

4 repeat

5 front := {y | y is successor node of some z from front and

6 y is not in reachable}

7 if x is in front then cycle from x to x exists, stop;

8 endif;

9 reachable := reachable ∪ front;

10 until front = {}

11 end

We can imagine breadth-ﬁrst search to be somewhat like the propagation

of waves that are created when a stone is thrown into a calm lake. The wave

9 Cycles in Graphs 87

front, the outermost wave, always contains the part of the water surface that

can be reached at a time.

The loop that is used in our breadth-ﬁrst search algorithm is repeated

at most as many times as there are nodes, usually much less often. (To be

precise, the running time is deﬁned by the longest path from one node to any

other node.)

Breadth-ﬁrst search can be a very fast and eﬃcient way to determine

whether some node is part of a cycle. (However, for ﬁnding all cycles we

would have to run breadth-ﬁrst search starting from all nodes, which would

lead to a big increase in running time in comparison to depth-ﬁrst search.)

For breadth-ﬁrst search, we need to set up and manage the two sets of nodes

front and reachable, which may contain very many nodes compared to depth-

ﬁrst search. The complexity, i.e., the time and space eﬃciency of the search,

depends on the eﬃciency of the set operations that are being used. With an

explicit representation of nodes and edges it is possible to implement breadth-

ﬁrst search in such a way that the running time is proportional to the number

of edges in the graph; see, e.g., the book by Sedgewick in the References below.

Large sets and relations can also be represented symbolically as so-called

binary decision diagrams. For such a representation, fast library functions

exist, which can be used to implement breadth-ﬁrst search very eﬃciently.

Historical Notes

The problem of ﬁnding cycles in graphs appeared early in the history of com-

puter science. The ﬁrst examples of application from the 1950s were the search

for loops in circuits or data ﬂow diagrams. Depth-ﬁrst search and recursive

algorithms for searching cycles in graphs have been known since the 1960s

and are often used as standard examples for backtracking. Tarjan’s algorithm

to calculate strongly connected components was published in 1972. A very

important application of algorithms used to ﬁnd cycles in graphs is to recog-

nize deadlocks in resource dependency graphs: in every multitasking operat-

ing system, cyclic waiting conditions can occur due to wrong synchronization.

Popular illustrations for this are Dijkstra’s dining philosophers or Lamport’s

bakery algorithm. Since the 1970s, more and more computer games have ap-

peared that have the player ﬁnd a way through a virtual labyrinth (a graph),

88 Holger Schlingloﬀ

where a multitude of dangers are waiting and cycles have to be avoided (e.g.,

Dungeons and Dragons). In the 1990s, new eﬃcient algorithms and data struc-

tures to recognize cycles and form quotients were developed for state space

exploration in the automatic veriﬁcation of models. These methods form the

basis for analyzing safety-critical control software in planes, trains, and auto-

mobiles.

References

1. Robert Sedgewick: Algorithms in {C|C++|Java},Part5:Graph Algo-

rithms. Addison-Wesley Professional, 3rd edition, 2003.

A classic textbook on algorithms that is continually updated and ex-

tended.

2. Thomas H. Cormen, Charles Leiserson, Ronald L. Rivest, Cliﬀord Stein:

Introduction to Algorithms. MIT Press, 2001.

Another widely used book on the topic.

3. Robert E. Tarjan: Depth-ﬁrst search and linear graph algorithms.SIAM

Journal on Computing 1 (2), pp. 146–160, 1972.

The original reference for the algorithm for strongly connected compo-

nents.

4. Edsger W. Dijkstra: Hierarchical ordering of sequential processes. Acta

Informatica 1 (2), pp. 115–138, 1971.

http://www.cs.utexas.edu/users/EWD/ewd03xx/EWD310.PDF

The original reference for the dining philosophers analogy.

5. Leslie Lamport: A new solution of Dijkstra’s concurrent programming

problem. Comm. ACM 17 (8), pp. 453–455, Aug. 1974.

http://research.microsoft.com/en-us/um/people/lamport/pubs/

bakery.pdf

The original reference for the bakery algorithm to synchronize the parallel

access to shared resources.

6. Wikipedia articles describing the topics of this chapter:

• Depth-ﬁrst search: http://en.wikipedia.org/wiki/Depth-first

• Breadth-ﬁrst search: http://en.wikipedia.org/wiki/Breadth-

first

• Tarjan’s algorithm: http://en.wikipedia.org/wiki/Tarjan’s

strongly connected components algorithm

Acknowledgement

The author wishes to thank Laura Schlingloﬀ for help with the pictures and

translation.

PageRank – What Is Really Relevant

in the World-Wide Web?

Ulrik Brandes and Gabi Dorfm¨uller

Universit¨at Konstanz, Konstanz, Germany

No doubt, the most popular form of Internet usage is the World-Wide Web

(WWW), a network of billions of ﬁles. It is made up, for the most part, of

Web pages containing text and images that refer to each other via (hyper)links.

Even if you spent your whole life, day and night, doing nothing but browsing

pages, you’d see only a small fraction of the Web.

To ﬁnd something on the

Web, it is therefore necessary to know where it is, or what links there.

Practically everyone surﬁng the Web therefore uses search engines, i.e.,

special pages on which the information sought is described using a few key

words (query) to obtain a list of pages that may be relevant to the query (hits).

Using many computer science methods, modern search engines are capable of

organizing access to billions of Web pages, and scanning them for matches

with a query within fractions of a second.

Since even a query term such as algorithm yields millions of hits, the results

themselves are too large to be read completely. Search engines therefore sort

their results in such a way that the seemingly most relevant hits are shown

ﬁrst.

Quiz:

How do search engines manage to ﬁnd Web pages that seem relevant to us

out of the millions matching a typical query?

As of today, the best known search engine is run by a company called

Google,

since it was the ﬁrst search engine to not only sift through an enor-

mous number of pages, but also to use a particularly clever algorithm to rank

the results. Among, e.g., more than a million German-language hits matching

Algorithmus, the site of the original project leading to this book currently

ranks second only to the corresponding Wikipedia article.

Assume that you are spending a second per page – how many seconds does an

average life last?

www.google.com

B. V¨ocking et al. (eds.), Algorithms Unplugged,

DOI 10.1007/978-3-642-15328-0

10,

 Springer-Verlag Berlin Heidelberg 2011